Nội dung toàn văn Tiêu chuẩn Việt Nam TCVN 6910-2:2001 (ISO 5725-2 : 1994) về Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 2: Phương pháp cơ bản xác định độ lặp lại và độ tái lập của phương pháp đo tiêu chuẩn do Bộ Khoa học Công nghệ và Môi trường ban hành
TIÊU CHUẨN VIỆT NAM
TCVN 6910-2:2001
ISO 5725-2 : 1994
ĐỘ CHÍNH XÁC (ĐỘ ĐÚNG VÀ ĐỘ CHỤM) CỦA PHƯƠNG PHÁP ĐO VÀ KẾT QUẢ ĐO – PHẦN 2: PHƯƠNG PHÁP CƠ BẢN XÁC ĐỊNH ĐỘ LẶP LẠI VÀ ĐỘ TÁI LẬP CỦA PHƯƠNG PHÁP ĐO TIÊU CHUẨN
Accuracy (trueness and precision) of measurement methods and results – Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method
Lời nói đầu
TCVN 6910-2 : 2001 hoàn toàn tương đương với ISO 5725-2 : 1994
Phụ lục A của tiêu chuẩn này là quy định, các phụ lục B và C chỉ để tham khảo.
TCVN 6910-2 : 2001 do Tiểu ban Kỹ thuật Tiêu chuẩn TCVN/ TC69/ SC6
Phương pháp và Kết quả đo biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị. Bộ Khoa học công nghệ và Môi trường ban hành.
Lời giới thiệu
0.0 TCVN 6910-2: 2001 là một phần của TCVN 6910, bộ tiêu chuẩn này gồm 6 phần dưới tên chung “Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo”:
– Phần 1: Nguyên tắc và định nghĩa chung
– Phần 2: Phương pháp cơ bản xác định độ lặp lại và độ tái lập của phương pháp đo tiêu chuẩn
– Phần 3: Các thước đo trung gian độ chụm của phương pháp đo tiêu chuẩn
– Phần 4: Các phương pháp cơ bản xác định độ đúng của phương pháp đo tiêu chuẩn
– Phần 5: Các phương pháp khác để xác định độ chụm của phương pháp đo tiêu chuẩn
– Phần 6: Sử dụng các giá trị độ chính xác trong thực tế
0.1 TCVN 6910 sử dụng hai thuật ngữ “độ đúng” và “độ chụm” để mô tả độ chính xác của phương pháp đo. “Độ đúng” chỉ mức độ gần nhau giữa trung bình số học của một số lớn các kết quả thử nghiệm và giá trị thực hoặc giá trị qui chiếu được chấp nhận. “Độ chụm” chỉ mức độ gần nhau giữa các kết quả thử nghiệm.
0.2 Sự xem xét tổng quát về các đại lượng này được trình bày trong TCVN 6910-1 nên không được nhắc lại ở tiêu chuẩn này. TCVN 6910-1 nên được đọc kết hợp cùng với tất cả các phần khác của TCVN 6910, kể cả tiêu chuẩn này, bởi vì những định nghĩa cơ sở và những nguyên tắc tổng quát đều được trình bày trong tiêu chuẩn đó.
0.3 Tiêu chuẩn này chỉ liên quan đến việc ước lượng độ lệch chuẩn lặp lại và độ lệch chuẩn tái lập. Mặc dù các loại thí nghiệm khác (như thí nghiệm phân mức) trong những bối cảnh nhất định được dụng để ước lượng độ chụm, nhưng chúng không được đề cập đến ở tiêu chuẩn này mà là đối tượng của TCVN 6910-5. Tiêu chuẩn này cũng không quan tâm đến những thước đo trung gian độ chụm giữa hai thước đo chính; chúng là đối tượng của TCVN 6910-3.
0.4. Trong những bối cảnh nhất định, dữ liệu thu được trong thí nghiệm để ước lượng độ chụm cũng sử dụng để ước lượng độ đúng. Ước lượng độ đúng không được quan tâm đến ở tiêu chuẩn này; nó là đối tượng của TCVN 6910-4.
ĐỘ CHÍNH XÁC (ĐỘ ĐÚNG VÀ ĐỘ CHỤM) CỦA PHƯƠNG PHÁP ĐO VÀ KẾT QUẢ ĐO – PHẦN 2: PHƯƠNG PHÁP CƠ BẢN XÁC ĐỊNH ĐỘ LẶP LẠI VÀ ĐỘ TÁI LẬP CỦA PHƯƠNG PHÁP ĐO TIÊU CHUẨN
Accuracy (trueness and precision) of measurement methods and results – Part 2: Basic method for the determination of repeatability and reproducibility of a standard measurement method
1. Phạm vi áp dụng
1.1. Tiêu chuẩn này
– làm rõ các nguyên tắc chung được tuân thủ trong thiết kế thí nghiệm ước lượng độ chụm của các phương pháp đo thông qua thí nghiệm phối hợp liên phòng;
– mô tả thực tế, chi tiết phương pháp cơ bản để sử dụng rộng rãi khi ước lượng độ chụm của phương pháp đo;
– đưa ra hướng dẫn cho tất cả mọi người liên quan đến việc thiết kế, thực hiện hoặc phân tích kết quả của những phép thử nghiệm ước lượng độ chụm.
Chú thích 1 – Những biến đổi của phương pháp cơ bản này cho những mục đích riêng được trình bày ở các phần khác của TCVN 6910
Phụ lục B đưa ra những ví dụ thực tế ước lượng độ chụm của phương pháp đo bằng thực nghiệm.
1.2. Tiêu chuẩn này liên quan riêng đến các phương pháp đo tạo ra những phép đo trên thang đo liên tục và cho kết quả thử nghiệm là giá trị đơn, tuy giá trị đơn này có thể là kết quả tính toán từ một tập hợp các quan trắc.
1.3. Giả thiết là tất cả các nguyên tắc đưa ra ở TCVN 6910-1 được tuân thủ trong thiết kế và tiến hành thí nghiệm độ chụm. Phương pháp cơ bản này sử dụng cùng một số lượng các kết quả thử nghiệm trong từng phòng thí nghiệm, phân tích các mức như nhau của mẫu thử; tức là: thí nghiệm đồng mức cân bằng. Phương pháp cơ bản này áp dụng cho các quy trình được tiêu chuẩn hoá và sử dụng thường xuyên ở nhiều phòng thí nghiệm.
Chú thích 2 – Các ví dụ được đưa ra để giải thích các tập hợp kết quả thử nghiệm đồng nhất được cân bằng, tuy trong một ví dụ số lượng thay đổi của các phép lặp cho từng ô được ghi lại (thiết kế không cân bằng) và trong ví dụ khác thiếu một số dữ liệu. Đó là vì thí nghiệm được thiết kế để cân bằng có thể trở nên mất cân bằng. Ví dụ cũng đề cập đến các giá trị tản mạn và các giá trị bất thường.
1.4. Mô hình thống kê trong điều 5 của TCVN 6910-1: 2001 được chấp nhận là cơ sở thích hợp để trình bày và phân tích kết quả thử nghiệm với phân bố xấp xỉ chuẩn.
1.5. Tiêu chuẩn này trình bày phương pháp cơ bản để ước lượng độ chụm của phương pháp đo:
a) Khi yêu cầu xác định độ lệch chuẩn lặp lại và tái lập như định nghĩa trong TCVN 6910-1;
b) Khi vật liệu sử dụng đồng nhất hoặc khi tác dụng của tính không đồng nhất có thể bao hàm trong giá trị độ chụm;
c) Khi chấp nhận việc sử dụng cách bố trí đồng mức cân bằng.
1.6. Sự tiếp cận tương tự có thể được sử dụng để đưa ra ước lượng ban đầu của độ chụm đối với những phương pháp đo chưa được tiêu chuẩn hoá hoặc không thông dụng.
2. Tiêu chuẩn viện dẫn
ISO 3534-1-1993 Thống kê học – Từ vựng và kí hiệu – Phần 1: Thuật ngữ về xác suất thống kê đại cương
TCVN 6910-1:2001 Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 1: Nguyên tắc và định nghĩa chung.
3. Định nghĩa
Những định nghĩa đưa ra ở ISO 3534-1 và TCVN 6910-1 được áp dụng trong TCVN 6910-2.
Những ký hiệu sử dụng trong TCVN 6910 ở phụ lục A.
4. Ước lượng các tham số trong mô hình cơ sở
4.1. Những quy trình đưa ra trong tiêu chuẩn này dựa trên mô hình thống kê đưa ra trong điều 5 của TCVN 6910-1: 2001 và được chi tiết hoá trong 1.2 của TCVN 6910-1: 2001. Cụ thể, những quy trình này dựa trên cơ sở các phương trình (2) đến (6) trong 5 của TCVN 6910-1: 2001
Mô hình đó là:
y = m + B + e
trong đó, với mỗi vật liệu cụ thể được thử nghiệm:
m là trung bình chung (kỳ vọng);
B là thành phần phòng thí nghiệm của độ chệch trong điều kiện lặp lại;
e là sai số ngẫu nhiên xuất hiện ở mọi phép đo trong điều kiện lặp lại.
4.2. Các phương trình từ (2) đến (6) tại điều 5 trong TCVN 6910-1: 2001 được thể hiện bằng độ lệch chuẩn thực của các phân bố được đề cập. Trên thực tế, không biết giá trị chính xác của những độ lệch chuẩn ấy và ước lượng của các giá trị độ chụm phải thực hiện từ một mẫu tương đối nhỏ của tất cả những phòng thí nghiệm có thể, và từ mẫu nhỏ của tất cả các kết quả thử nghiệm có thể trong phạm vi những phòng thí nghiệm này.
4.3. Trong thực tế thống kê, khi giá trị thực của độ lệch chuẩn s không được biết và được thay thế bằng ước lượng trên cơ sở mẫu thì ký hiệu s được thay thế bằng s để biểu thị đó là giá trị ước lượng. Điều đó được thực hiện ở tất cả các phương trình từ (2) đến (6) trong TCVN 6910-1 : 2001, với:
SL2 là ước lượng của phương sai giữa các phòng thí nghiệm:
Sw2 là ước lượng của phương sai trong phạm vi phòng thí nghiệm;
sr2 là trung bình số học của Sw2 và là ước lượng của phương sai lặp lại; trung bình số học này được tính với tất cả các phòng tham gia thí nghiệm độ chính xác được giữ lại sau khi loại bỏ các phòng thí nghiệm bất thường;
SR2 là ước lượng của phương sai tái lập:
SR2 = SL2 + Sr2 …………..(1)
5. Yêu cầu đối với thí nghiệm độ chụm
5.1. Bố trí thí nghiệm
5.1.1. Trong phương pháp cơ bản, các mẫu lấy từng lô vật liệu đại diện cho q mức khác nhau của phép thử nghiệm được gửi cho p phòng thí nghiệm. Mỗi phòng thí nghiệm này thu được chính xác n kết quả thử nghiệm lặp lại trong điều kiện lặp lại ở từng mức trong q mức khác nhau. Loại thí nghiệm này được gọi là thí nghiệm đồng mức cân bằng.
5.1.2. Việc thực hiện các phép đo đó cần được tổ chức và các hướng dẫn được đưa ra như sau:
a) Bất kỳ sự kiểm tra ban đầu nào của thiết bị đều phải theo quy định trong phương pháp tiêu chuẩn.
b) Mỗi nhóm n phép đo thuộc một mức được tiến hành trong các điều kiện lặp lại, ví dụ trong một thời gian ngắn, bởi cùng một người, và không có bất kỳ phép hiệu chuẩn lại thiết bị giữa chừng nào trừ khi đó là một phần không thể thiếu của phép đo.
c) Điều quan trọng là một nhóm n phép thử nghiệm được thực hiện trong những điều kiện lặp lại như là n phép thử nghiệm trên các vật liệu khác nhau. Tuy vậy, như là một quy tắc, thao tác viên sẽ biết rằng họ đang thử nghiệm vật liệu giống hệt nhau, nhưng phải nhấn mạnh trong các hướng dẫn rằng toàn bộ mục đích của thí nghiệm là xác định sự khác nhau giữa các kết quả có thể xuất hiện trong thử nghiệm thực tế. Nếu vẫn lo ngại những kết quả trước có thể ảnh hưởng đến kết quả thử nghiệm tiếp theo và như vậy ảnh hưởng đến phương sai độ lặp lại, thì nên cân nhắc có sử dụng được hay không n mẫu riêng biệt tại từng mức của q mức được mã hoá để thao tác viên sẽ không biết được những mẫu lặp lại ở một mức đã cho. Tuy nhiên một qui trình như vậy có thể gây ra những khó khăn trong việc đảm bảo những điều kiện lặp lại sẽ được áp dụng giữa các mẫu lặp lại. Điều này chỉ có thể thực hiện khi tất cả qn phép đo có thể thực hiện trong khoảng thời gian ngắn.
d) Không cần thiết phải thực hiện tất cả q nhóm của n phép đo một cách nghiêm ngặt trong khoảng thời gian ngắn; những nhóm khác nhau của các phép đo có thể được tiến hành trong những ngày khác nhau.
e) Các phép đo của tất cả q mức phải do một thao tác viên thực hiện và n phép đo ở mức nhất định phải thực hiện với cùng một thiết bị trong suốt quá trình đo.
f) Trong một đợt đo, nếu thao tác viên không tiếp tục được công việc thì thao tác viên khác có thể hoàn thành các phép đo với điều kiện là sự thay đổi đó không xảy ra trong nhóm n phép đo ở một mức mà chỉ xảy ra giữa hai trong q nhóm. Mọi sự thay đổi như vậy phải được thông báo cùng với kết quả.
g) Cần đưa ra giới hạn thời gian mà tất cả các phép đo phải hoàn thành. Điều này có thể là cần thiết để giới hạn thời gian cho phép giữa ngày nhận mẫu và ngày mà các phép đo được thực hiện.
h) Tất cả các mẫu phải được đánh dấu một cách rõ ràng với tên của thí nghiệm và sự nhận dạng mẫu.
5.1.3. Đối với một số phép đo, thực tế có thể có một nhóm thao tác viên mà mỗi thao tác viên của nhóm thực hiện một phần nào đó của qui trình. Trong trường hợp như vậy nhóm thao tác viên phải được coi là một “thao tác viên”. Bất kỳ sự thay đổi nào trong nhóm đều phải được coi như “thao tác viên” khác.
5.1.4. Trong thực tế thương mại, các kết quả thử nghiệm có thể được làm tròn số một cách rất thô, nhưng trong thí nghiệm độ chụm, các kết quả thử nghiệm cần được ghi lại ít nhất với số thập phân nhiều hơn số được chỉ định trong phương pháp tiêu chuẩn. Nếu phương pháp đó không chỉ ra số thập phân làm tròn thì phép làm tròn số không được thô hơn một nửa giá trị ước lượng của độ lệch chuẩn độ lặp lại. Khi độ chụm phụ thuộc vào mức m, phải có mức độ làm tròn số khác nhau cho các mức khác nhau.
5.2. Tuyển chọn các phòng thí nghiệm
Các nguyên tắc tổng quát đối với việc tuyển chọn các phòng thí nghiệm tham gia thí nghiệm liên phòng đã trình bày ở 6.3 trong TCVN 6910-1: 2001. Khi tuyển lựa sự hợp tác của một số phòng thí nghiệm cần nói rõ trách nhiệm của các phòng thí nghiệm này. Hình 1 là ví dụ về một phiếu hỏi tuyển chọn thích hợp.
5.2.2. Trong TCVN 6910-2. “phòng thí nghiệm” được xem là sự kết hợp của thao tác viên, thiết bị và nơi thử nghiệm. Một nơi thử nghiệm (hay phòng thí nghiệm theo nghĩa thông thường) có thể tạo ra một vài “phòng thí nghiệm” nếu có thể có một vài thao tác viên cùng với những tập hợp thiết bị độc lập để tiến hành công việc.
5.3. Chuẩn bị vật liệu
5.3.1. Sự thảo luận về những điểm cần cân nhắc đến khi lựa chọn vật liệu sử dụng trong thí nghiệm độ chụm trình bày ở 6.4 trong TCVN 6910-1: 2001.
5.3.2. Khi quyết định số lượng vật liệu cần cung cấp phải quy định số lượng cho phép do thất thoát, do sự cố hoặc do các lỗi khi thu nhận một số kết quả thử nghiệm mà có thể cần sử dụng thêm vật liệu. Số lượng vật liệu chuẩn bị phải đủ cho thí nghiệm và cho phép dự phòng một lượng thỏa đáng.
|
Phiếu hỏi về tham gia nghiên cứu liên phòng Tên phương pháp đo …………………………………………………………………………………. 1. Phòng thí nghiệm chúng tôi đồng ý tham gia thí nghiệm độ chụm đối với phương pháp đo tiêu chuẩn này. 2. Có £ Không £ (đánh dấu vào ô thích hợp) 2. Là người tham gia, chúng tôi hiểu rằng: a) Tất cả những thiết bị chính, hoá chất và các yêu cầu khác quy định trong phương pháp phải có trong phòng thí nghiệm của chúng tôi khi chương trình bắt đầu; b) Những yêu cầu quy định về thời gian, như thời điểm bắt đầu: thứ tự của các mẫu thử nghiệm và thời điểm kết thúc của chương trình phải được tuân thủ chặt chẽ; c) Phải tuân thủ chặt chẽ phương pháp; d) Mẫu thử nghiệm phải được xử lý phù hợp với các hướng dẫn; e) Các phép đo phải do thao tác viên lành nghề thực hiện. Sau khi nghiên cứu phương pháp và đánh giá đúng mức khả năng và trang thiết bị của mình, chúng tôi cho rằng mình đã sẵn sàng cho hợp tác thử nghiệm phương pháp này. 3. Góp ý (Ký tên) ……………………………………………………. (Công ty hoặc phòng thí nghiệm)………………………….
|
Hình 1 – Phiếu hỏi tham gia cho nghiên cứu liên phòng
5.3.3. Phải cân nhắc xem có cần thiết để một số phòng thí nghiệm thu về một vài kết quả thử nghiệm ban đầu để làm quen với phương pháp đo ước khi lấy kết quả thử nghiệm chính thức không, và nếu như vậy thì có nên chuẩn bị vật liệu bổ sung (không phải mẫu thí nghiệm độ chụm) cho mục đích này không.
5.3.4. Nếu vật liệu phải làm cho đồng nhất, yêu cầu này cần phải được thực hiện bằng một phương pháp thích hợp nhất đối với loại vật liệu ấy. Nếu vật liệu để thử nghiệm không đồng nhất thì điều rất quan trọng là chuẩn bị mẫu bằng cách được chỉ định trong phương pháp; tốt nhất là bắt đầu với một lô vật liệu thương phẩm đối với từng mức. Trong trường hợp vật liệu không ổn định, cần quy định các hướng dẫn riêng về cất giữ và bảo quản.
5.3.5. Đối với mẫu của từng mức, nên sử dụng n thùng chứa riêng biệt cho từng phòng thí nghiệm nếu có sự nguy hiểm của vật liệu bị hư hỏng khi mở thùng chứa (ví dụ do oxy hoá, do mất thành phần dễ bay hơi, hay với vật liệu hút ẩm). Trường hợp vật liệu không ổn định, cần quy định các hướng dẫn riêng về cất giữ và bảo quản. Cần cẩn thận trọng để đảm bảo rằng các mẫu thí nghiệm không thay đổi cho đến khi phép đo được thực hiện. Đặc biệt cần quan tâm khi vật liệu chứa hỗn hợp các loại bột với mật độ tương đối khác nhau hoặc với kích thước hạt khác nhau, vì nó có thể phân tách do lắc, ví dụ trong khi vận chuyển. Nếu có thể xảy ra phản ứng với môi trường, mẫu thí nghiệm có thể được đóng kín trong ống thủy tinh chân không hoặc với khí trơ. Đối với vật liệu dễ hư thối như thức ăn hoặc mẫu máu, cần giữ chúng ở trạng thái lạnh sâu khi gửi tới các phòng thí nghiệm tham gia cùng với những hướng dẫn chi tiết cho quá trình làm tan băng.
6. Nhân sự trong thí nghiệm độ chụm
Chú thích 3 – Các phương pháp thao tác dùng trong phạm vi các phòng thí nghiệm khác nhau khó có thể giống hệt nhau. Vì vậy nội dung mục này chỉ như một hướng dẫn có thể được sửa đổi cho phù hợp với một tình huống cụ thể.
6.1. Hội đồng
6.1.1. Hội đồng cần bao gồm những chuyên gia quen thuộc với phương pháp đo và việc ứng dụng chúng.
6.1.2. Nhiệm vụ của hội đồng gồm:
a) Lập kế hoạch và điều phối thí nghiệm;
b) Quyết định số phòng thí nghiệm, số mức, số phép đo thực hiện và số lượng các chữ số có nghĩa cần thiết:
c) Chỉ định người thực hiện nhiệm vụ thống kê;
d) Chỉ định người thực hiện nhiệm vụ điều hành;
e) Xem xét các hướng dẫn sẽ ban hành cho những người giám sát phòng thí nghiệm để bổ sung cho phương pháp đo tiêu chuẩn.
f) Quyết định có cho phép hay không một số thao tác viên thực hiện một số ít các phép đo không chính thức để thu lượm kinh nghiệm của phương pháp sau một thời gian dài (những phép đo như vậy sẽ không được thực hiện trên các mẫu liên phòng chính thức);
g) Thảo luận về các báo cáo phân tích thống kê khi thực hiện việc phân tích kết quả thử nghiệm.
h) Thiết lập các giá trị cuối cùng cho độ lệch chuẩn lặp lại và độ lệch chuẩn tái lập;
i) Quyết định các hành động cần thiết tiếp theo để cải tiến tiêu chuẩn về phương pháp đo hoặc về việc lưu ý đến các phòng thí nghiệm có kết quả đo bị loại bỏ như những giá trị bất thường.
6.2. Nhiệm vụ thống kê
Ít nhất một người trong hội đồng phải có kinh nghiệm về thiết lập và phân tích thống kê thí nghiệm.
Nhiệm vụ của người đó là:
a) Đóng góp kiến thức chuyên ngành của mình vào việc thiết kế thí nghiệm;
b) Phân tích số liệu;
c) Viết báo cáo cho Hội đồng theo hướng dẫn trong 7.7.
6.3. Nhiệm vụ điều hành
6.3.1. Việc tổ chức thí nghiệm trên thực tế phải giao cho một phòng thí nghiệm. Một người nào đó trong nhân sự của phòng thí nghiệm phải chịu toàn bộ trách nhiệm; người đó được gọi là người điều hành và do hội đồng chỉ định.
6.3.2. Nhiệm vụ của người điều hành là:
a) Tiếp nhận sự hợp tác của các phòng thí nghiệm cần thiết và đảm bảo rằng những người giám sát là người đã được chỉ định;
b) Tổ chức và giám sát sự chuẩn bị vật liệu, mẫu và sự phân chia mẫu; dành riêng ra một số lượng cần thiết vật liệu để dự phòng cho ở mỗi mức.
c) Dự thảo các hướng dẫn bao gồm các điểm từ mục a) đến h) trong 5.1.2 và lần lượt chuyển chúng đến các giám sát viên đủ sớm để họ nêu lên những ý kiến nhận xét hoặc các câu hỏi và để đảm bảo rằng những người thực hiện thí nghiệm được chọn là những người có thể thực hiện bình thường các phép đo hàng ngày;
d) Thiết kế các biểu mẫu thích hợp để thao tác viên ghi chép công việc và để giám sát viên thông báo các kết quả thử nghiệm với số chữ số có nghĩa cần thiết (các biểu mẫu như vậy có thể bao gồm tên của thao tác viên, thời gian nhận mẫu và đo mẫu, thiết bị được sử dụng và những thông tin liên quan);
e) Xử lý thắc mắc của các phóng thí nghiệm liên quan đến việc thực hiện các phép đo;
f) Giám sát để thời gian biểu được duy trì;
g) Thu thập các bằng số liệu và chuyển chúng đến chuyên gia thống kê.
6.4. Giám sát viên
6.4.1. Nhân viên ở mỗi phòng thí nghiệm tham gia thí nghiệm phải được giao trách nhiệm về tổ chức thực hiện các phép đo, thực hiện các hướng dẫn nhận được từ người điều hành, và báo cáo các kết quả thử nghiệm.
6.4.2. Nhiệm vụ của người giám sát là:
a) Đảm bảo những thao tác viên được chọn là những người có thể tiến hành bình thường các phép đo đó một cách quen thuộc.
b) Phân phát mẫu cho các thao tác viên theo đúng hướng dẫn của người điều hành (và khi cần thiết cung cấp vật liệu cho các thí nghiệm tương tự);
c) Giám sát việc thực hiện các phép đo (người giám sát không được tham gia thực hiện các phép đo);
d) Đảm bảo thao tác viên tiến hành đủ số lượng cần thiết các phép đo;
e) Đảm bảo thực hiện đúng thời gian biểu đã thiết lập cho việc thực hiện các phép đo;
f) Thu thập các kết quả thử nghiệm đã được ghi lại đến số thập phân thoả thuận, bao gồm cả sự bất thường, những khó khăn gặp phải và những ý kiến nhận xét của thao tác viên.
6.4.3. Giám sát viên của từng phòng thí nghiệm cần viết báo cáo đầy đủ gồm các thông tin sau:
a) Các kết quả thử nghiệm do người thao tác điền một cách rõ ràng vào biểu mẫu đã được cấp, không được sao chép hoặc đánh máy lại (bản in từ máy vi tính hoặc từ thiết bị thử nghiệm có thể được chấp nhận);
b) Các giá trị quan trắc hay số đọc gốc (nếu có), để tính ra kết quả thử nghiệm, đã được thao tác viên điền một cách rõ ràng vào biểu mẫu đã được cấp, không được sao chép hoặc đánh máy lại.
c) Ý kiến của các thao tác viên về tiêu chuẩn của phương pháp đo;
d) Thông tin về mọi sự bất thường hoặc sự gián đoạn đã có thể xảy ra trong quá trình đo, bao gồm mọi sự thay đổi về người thao tác, sự trình bày về phép đo nào do ai thực hiện, và những lý do làm thiếu kết quả;
e) Ngày nhận được mẫu;
f) Ngày mẫu được đo;
g) Thông tin về thiết bị sử dụng, nếu liên quan;
h) Mọi thông tin có liên quan khác.
6.5. Thao tác viên
6.5.1. Ở từng phòng thí nghiệm, các phép đo cần phải thực hiện bởi một thao tác viên được chọn là người đại diện cho những người có khả năng thực hiện các phép đo đó một cách bình thường.
6.5.2. Vì mục đích của thí nghiệm là xác định độ chụm thu được từ các thao tác viên đang làm việc với phương pháp đo tiêu chuẩn, do vậy không nên quá đề cao vai trò của các thao tác viên. Tuy nhiên, cần chỉ ra cho các thao tác viên biết rằng mục tiêu của thí nghiệm là để phát hiện ra phạm vi các kết quả có thể thay đổi trong thực tế, do vậy sẽ giảm thiểu được xu hướng loại bỏ hay làm lại các kết quả mà họ cảm thấy là không phù hợp.
6.5.3. Tuy bình thường thao tác viên không có vai trò bổ sung thêm vào phương pháp đo tiêu chuẩn, nhưng họ cần được khuyến khích góp ý vào tiêu chuẩn, đặc biệt phát biểu xem những hướng dẫn đó đã đầy đủ và rõ ràng chưa.
6.5.4. Nhiệm vụ của thao tác viên là:
a) Thực hiện các phép đo theo phương pháp đo tiêu chuẩn;
b) Báo cáo mọi sự bất bình thường hay khó khăn vấp phải; báo cáo về một sai lỗi tốt hơn là điều chỉnh kết quả thử nghiệm vì việc thiếu một hoặc hai kết quả sẽ không làm hỏng thí nghiệm và sẽ chỉ ra thiếu sót của tiêu chuẩn.
c) Góp ý về sự đầy đủ của các hướng dẫn trong tiêu chuẩn; thao tác viên cần báo cáo mọi trường hợp không thể thực hiện được theo hướng dẫn cũng như khi điều này có thể chỉ ra thiếu sót của tiêu chuẩn.
7. Phân tích thống kê thí nghiệm độ chụm
7.1. Xem xét ban đầu
7.1.1. Việc phân tích thống kê số liệu cần được giải quyết bởi chuyên gia thống kê theo ba giai đoạn liên tiếp sau:
a) Đánh giá số liệu để nhận biết và xử lý những giá trị bất thường hoặc những sự không bình thường khác và để kiểm nghiệm sự thích hợp của mô hình:
b) Tính toán các giá trị ban đầu của độ chụm và các giá trị trung bình cho từng mức riêng biệt;
c) Thiết lập giá trị cuối cùng của độ chụm và các giá trị trung bình, kể cả việc thiết lập mối quan hệ giữa độ chụm và mức m nếu có.
7.1.2. Ở từng mức riêng biệt sự phân tích thống kê trước tiên là tính các ước lượng của:
– Phương sai lặp lại ![]()
– Phương sai giữa các phòng thí nghiệm sL2
– Phương sai tái lập sR2 = sr2 + sL2
– Giá trị trung bình m.
7.1.3. Sự phân tích bao gồm việc áp dụng một cách hệ thống những phép thử thống kê đối với những giá trị bất thường mà sự đa dạng của những thí nghiệm này có thể thấy trong tài liệu và chúng có thể được sử dụng cho mục đích của TCVN 6910-2. Vì lý do thực tế nên chỉ tập hợp một số giới hạn những phép thử đó, như giải thích trong 7.3.
7.2. Lập bảng kết quả và ghi chép
7.2.1. Ô
Mỗi một tổ hợp của phòng thí nghiệm và một mức được gọi là một ô của thí nghiệm độ chụm. Trong trường hợp lý tưởng, các kết quả của thí nghiệm với p phòng thí nghiệm và q mức tạo nên một bảng với pq ô, mỗi một ô chứa n kết quả thử nghiệm lặp lại có thể sử dụng để tính độ lệch chuẩn lặp lại và độ lệch chuẩn tái lập. Tuy nhiên, tình huống lý tưởng này không thường xuyên có được trong thực tế. Sự sai lệch ấy xuất hiện cùng với các số liệu thừa, thiếu và những giá trị bất thường.
7.2.2. Số liệu thừa
Đôi khi phòng thí nghiệm có thể tiến hành và báo cáo nhiều hơn n kết quả thử nghiệm đã được quy định. Trong trường hợp đó người giám sát cần báo cáo tại sao điều đó xảy ra và những kết quả nào là đúng. Nếu tất cả các kết quả đó có ý nghĩa ngang nhau thì nên tiến hành lựa chọn ngẫu nhiên từ những kết quả thử nghiệm có được để lấy ra số lượng kết quả đã định để phân tích.
7.2.3. Số liệu thiếu
Trong trường hợp khác, một số kết quả thử nghiệm có thể thiếu do mất mẫu hoặc sai sót trong khi tiến hành đo. Theo sự phân tích trong 7.1 có thể loại bỏ một cách đơn giản những ô hoàn toàn rỗng, những ô rỗng một phần có thể xem xét tính toán theo qui trình tính toán tiêu chuẩn.
7.2.4. Giá trị bất thường
Những giá trị này nằm trong số những kết quả thử nghiệm gốc hoặc trong bảng giá trị đươc suy ra từ những kết quả đó nhưng lệch rất nhiều so với những kết quả tương ứng trong cùng một bảng đến mức được xem là rất khó hoà hợp với những kết quả khác. Kinh nghiệm cho thấy không phải lúc nào cũng tránh được các giá trị bất thường. Chúng phải được xem xét theo phương pháp tương tự như đối với việc xử lý số liệu thiếu.
7.2.5. Phòng thí nghiệm bất thường
Khi xuất hiện một số kết quả thử nghiệm bất thường không giải thích được ở các mức khác nhau trong cùng một phòng thí nghiệm, phương sai trong phòng thí nghiệm này sẽ là quá cao và/hoặc sai số hệ thống ở mức của các kết quả thử nghiệm là quá lớn thì phòng thí nghiệm ấy có thể xem là bất thường. Do vậy có cơ sở để loại bỏ một số hoặc tất cả các số liệu của phòng thí nghiệm bất thường như vậy.
Tiêu chuẩn này không đưa ra phép thử thống kê để có thể đánh giá các phòng thí nghiệm nghi ngờ. Quyết định đầu tiên thuộc trách nhiệm của chuyên gia thống kê, nhưng tất cả các phòng thí nghiệm bị loại bỏ phải được thông báo cho hội đồng để có các hành động tiếp theo.
7.2.6. Số liệu sai
Thông thường, các số liệu sai phải được phát hiện và hiệu chính hoặc loại bỏ.
7.2.7. Các kết quả thử nghiệm đồng mức cân bằng
Trường hợp lý tưởng là p phòng thí nghiệm được gọi là i (i = 1, 2,… p), mỗi mức thử q gọi Ià j (j = 1, 2, … q) với n phép lặp lại ở mỗi mức (mỗi tổ hợp ij), sẽ cho tất cả là pqn kết quả thử nghiệm. Do kết quả thử nghiệm thiếu (7.2.3) hay sai lệch (7.2.4) hoặc do các phòng thí nghiệm bất thường (7.2.5) hay số liệu sai (7.2.6), cho nên không phải lúc nào cũng đạt được trường hợp lý tưởng. Trong những điều kiện như vậy các lưu ý đưa ra ở 7.2.8 đến 7.2.10 và các quy trình ở 7.4 được áp dụng đối với số lượng khác nhau của kết quả thử nghiệm. Mẫu của các dạng được khuyến nghị để dùng cho phân tích thống kê trình bày ở hình 2. Chúng có thể được đơn giản hoá cho phù hợp như biểu mẫu A, B và C (trong hình 2).
7.2.8. Kết quả thử nghiệm gốc
Xem biểu mẫu A trong hình 2, trong đó:
nij là số kết quả phép thử trong ô của phòng thí nghiệm i ở mức j;
yijk là một trong số các kết quả thử nghiệm này (k = 1, 2…. nij);
pj là số phòng thí nghiệm báo cáo ít nhất một kết quả thử nghiệm ở mức j (sau khi loại bỏ kết quả xem là bất thường hoặc sai)
|
Biểu mẫu A – Khuyến nghị cho việc tập hợp và sắp xếp số liệu gốc |
|||||||||
|
Phòng thí nghiệm |
Mức |
||||||||
|
|
1 |
2 |
… |
… |
j |
… |
… |
q – 1 |
q |
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
… … i … |
|
|
|
|
… … yijk … |
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
Biểu mẫu B – Khuyến nghị cho việc tập hợp và sắp xếp các giá trị trung bình |
|||||||||
|
Phòng thí nghiệm |
Mức |
||||||||
|
1 |
2 |
… |
… |
j |
… |
… |
q – 1 |
q |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
Biểu mẫu C – Khuyến nghị cho việc tập hợp và sắp xếp các thước đo của sự phân tán trong phạm vi ô |
|||||||||
|
Phóng thí nghiệm |
Mức |
||||||||
|
1 |
2 |
… |
… |
j |
… |
… |
q – 1 |
q |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
Sij |
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
Hình 2 – Các biểu mẫu khuyến nghị cho việc tập hợp và sắp xếp kết quả để phân tích
7.2.9. Giá trị trung bình của ô (biểu mẫu B trong hình 2)
Chúng được tính từ biểu mẫu A như sau:
![]() …(2)
…(2)
Giá trị trung bình ô phải được ghi lại với hơn một chữ số có nghĩa so với kết quả thử nghiệm trong biểu mẫu A.
7.2.10. Thước đo độ phân tán của ô (biểu mẫu C trong hình 2)
Chúng được tính từ biểu mẫu A (xem 7.2.8) và biểu mẫu B (xem 7.2.9) như sau:
Đối với trường hợp tổng quát, sử dụng độ lệch chuẩn trong phạm vi ô
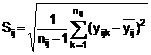 …(3)
…(3)
Hoặc tương tự
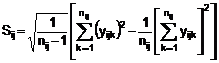 …(4)
…(4)
Khi dùng những công thức này phải chú ý để nhận được số lượng đầy đủ các chữ số trong tính toán: nghĩa là mọi giá trị trung gian phải được tính toán với ít nhất là gấp đôi chữ số có nghĩa trong số liệu gốc.
Chú thích 4 – Nếu ô ij chúa hai kết quả thử nghiệm, độ lệch chuẩn trong phạm vi ô sẽ là:
![]() …(5)
…(5)
Vì vậy, để đơn giản có thể sử dụng độ lệch tuyệt đối thay cho độ lệch chuẩn nếu tất cả các ô có hai kết quả thử nghiệm.
Độ lệch chuẩn phải được trình bày bằng số có hơn một chữ số có nghĩa so với kết quả trong biểu mẫu A.
Đối với những giá trị nij nhỏ hơn 2 phải điền gạch ngang (-) vào biểu mẫu C.
7.2.11. Số liệu hiệu chính hoặc loại bỏ
Vì một số số liệu có thể được hiệu chính hoặc loại bỏ trên cơ sở các phép thử nghiệm đề cập ở 7.1.3, 7.3.3 và 7.3.4, nên các giá trị yijk, nij và pj được sử dụng cho việc xác định giá trị cuối cùng độ chụm và giá trị trung bình có thể khác các giá trị dựa trên các kết quả thử nghiệm gốc như đã ghi lại trong các biểu mẫu A, B và C của hình 2. Do đó, khi báo cáo các giá trị cuối cùng của độ chụm và độ đúng luôn luôn phải nêu rõ những số liệu đã được hiệu chỉnh hoặc bị loại bỏ, nếu có.
7.3. Khảo sát kết quả về tính nhất quán và các giá trị bất thường
Xem tài liệu tham khảo [3].
Độ lệch chuẩn lặp lại và tái lập được ước lượng từ những số liệu thu được ở một số các mức xác định. Sự hiện diện của các phòng thí nghiệm hoặc các giá trị riêng biệt không nhất quán với tất cả các phòng thí nghiệm hoặc các giá trị khác có thể làm thay đổi các ước lượng, và phải đưa ra quyết định đối với những giá trị đó. Có hai cách tiếp cận:
a) Kỹ thuật nhất quán bằng đồ thị;
b) Phép thử giá trị bất thường bằng số.
7.3.1. Kỹ thuật nhất quán bằng đồ thị
Sử dụng hai thước đo là thống kê Mandel h và k. Hai số này vừa mô tả sự thay đổi của phương pháp đo vừa trợ giúp trong việc đánh giá phòng thí nghiệm.
7.3.1.1. Tính toán thống kê nhất quán giữa các phòng thí nghiệm, h, cho từng phòng thí nghiệm bằng cách chia độ lệch 6 (trung bình ô trừ đi trung bình chung ở mức đó) cho độ lệch chuẩn của các trung bình ô (ở mức đó):
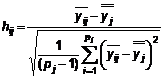 …(6)
…(6)
trong đó, với ![]() xem 7.2.9 và với
xem 7.2.9 và với ![]() xem 7.4.4
xem 7.4.4
Vẽ đồ thị các giá trị hij của từng ô theo thứ tự của phòng thí nghiệm, thành các nhóm ở từ mức (và phân tách thành từng nhóm cho một số mức được kiểm tra ở từng phòng thí nghiệm) (xem hình B.7).
7.3.1.2. Tính toán thống kê nhất quán trong phòng thí nghiệm, k, trước tiên phải tính độ lệch chuẩn chung trong ô ở từng mức
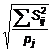
và sau đó tính kij cho từng phòng thí nghiệm ở từng mức
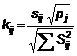 …..(7)
…..(7)
Lập đồ thị các giá trị Kij cho từng ô theo thứ tự của phòng thí nghiệm, thành các nhóm ở từng mức (và phân tách thành từng nhóm cho một số mức được kiểm tra ở từng phòng thí nghiệm) (xem hình B.8)
7.3.1.3. Việc kiểm tra đồ thị của h và k có thể chỉ ra rằng các phòng thí nghiệm cụ thể đưa ra những mẫu kết quả rất khác nhau. Điều này thể hiện sự thay đổi nhiều hay ít một cách nhất quán trong phạm vi một ô và/hoặc các giá trị trung bình cực trị của ô thể hiện ở nhiều mức. Nếu điều này xảy ra, phòng thí nghiệm cụ thể ấy cần được tiếp xúc để xác minh những nguyên nhân của sự không nhất quán. Trên cơ sở của những phát hiện đó nhà thống kê có thể:
a) Giữ lại các số liệu của phòng thí nghiệm một thời gian;
b) Yêu cầu phòng thí nghiệm sửa lại phép đo (nếu có thể);
c) Loại bỏ số liệu của phòng tní nghiệm ra khỏi việc nghiên cứu
7.3.1.4. Các mẫu khác nhau có thể xuất hiện trong đồ thị h. Tất cả các phòng thí nghiệm có thể có cả giá trị h dương và âm ở các mức khác nhau của thí nghiệm. Các phòng thí nghiệm riêng biệt có thể có xu hướng đưa ra tất cả các giá trị h là dương hoặc âm và số các phòng thí nghiệm đưa ra giá trị âm thì cũng gần tương đương với các phòng thí nghiệm đưa ra giá trị dương. Các mẫu đó không bất bình thường, cũng không đòi hỏi phải nghiên cứu, dù loại mẫu thứ hai có thể gợi ý về sự tồn tại nguồn gốc chung của độ chệch phòng thí nghiệm. Mặt khác, nếu tất cả các giá trị h của một phòng thí nghiệm cùng dấu và các giá trị h của các phòng thí nghiệm khác có dấu ngược lại thì cần tìm ra nguyên nhân. Tương tự như vậy, nếu các giá trị h của một phòng thí nghiệm là cực trị và xuất hiện phụ thuộc một cách có hệ thống vào mức của phép thử nghiệm thì cần tìm ra nguyên nhân. Những đường được vẽ trên đồ thị h tương ứng với các chỉ báo đưa ra ở ( bảng 6 và 7). Những đường chỉ báo này được sử dụng như các hướng dẫn khi kiểm tra mẫu theo các dữ liệu.
7.3.1.5. Nếu một phòng thí nghiệm không nằm trên đồ thị k vì có nhiều giá trị lớn thì cần tìm ra nguyên nhân: điều đó chứng tỏ rằng phòng thí nghiệm có độ lặp lại thấp hơn so với các phòng thí nghiệm khác. Phòng thí nghiệm có thể làm tăng các giá trị k nhỏ một cách phù hợp vì những yếu tố như làm tròn một cách quá mức các số liệu của nó hay thang đo không đủ nhậy. Các đường được vẽ trên các đồ thị tương ứng với các chỉ báo đưa ra ở 8.3 (các bảng 6 và 7). Những đường chỉ báo này được sử dụng như các hướng dẫn khi kiểm tra những mẫu theo các dữ liệu.
7.3.1.6. Nếu đồ thị h hoặc k được nhóm lại theo phòng thí nghiệm cho thấy phòng thí nghiệm nào đó có một số giá trị h hay k gần đường giá trị tới hạn, thì cần phải nghiên cứu đồ thị tương ứng đã được nhóm lại theo mức. Thường giá trị lớn trên đồ thị đã được nhóm lại theo phòng thí nghiệm sẽ trở nên nhất quán một cách hợp lý với các phòng thí nghiệm khác ở cùng một mức. Nếu có sự khác nhau rõ rệt so với giá trị của các phòng thí nghiệm khác thì cần phải tìm ra nguyên nhân.
7.3.1.7. Cùng với đồ thị của h và k, biểu đồ cột của các giá trị trung bình ô và phạm vi ô có thể có ví dụ hai tổng thể riêng biệt. Trường hợp như vậy đòi hỏi sự xử lý đặc biệt vì nguyên tắc chung của các phương pháp đã trình bày ở đây giả định chỉ có một tổng thể một đỉnh.
7.3.2. Kỹ thuật xử lý giá trị bất thường bằng số
7.3.2.1. Việc xử lý các giá trị bất thường được tiến hành như sau:
a) Các phép thử khuyến nghị trong 7.3.3 và 7.3.4 được áp dụng để nhận biết giá trị tản mạn hoặc giá trị bất thường:
– Nếu thống kê thử nghiệm nhỏ hơn hoặc bằng 5% giá trị tới hạn của nó, hạng mục kiểm tra được chấp nhận là đúng;
– Nếu thống kê thử nghiệm lớn hơn 5% và nhỏ hơn hoặc bằng 1% giá trị tới hạn của nó thì hạng mục thử nghiệm được gọi là giá trị tản mạn và được đánh dấu bằng hoa thị đơn.
– Nếu số thống kê thử nghiệm lớn hơn 1% giá trị tới hạn của nó thì hạng mục được gọi là giá trị bất thường thống kê và được đánh dấu bằng hoa thị kép.
b) Tiếp theo phát hiện xem liệu các giá trị tản mạn và/hoặc các giá trị bất thường thống kê có thể được giải thích bởi sai số về mặt kỹ thuật nào đó hay không, ví dụ:
– Sơ xuất khi thực hiện phép đo,
– Sai sót khi tính toán,
– Sai sót khi ghi chép kết quả thử nghiệm, hoặc
– Phân tích mẫu hỏng.
Khi sai sót là một trong các loại lỗi tính toán hoặc ghi chép thì kết quả sai cần được thay thế bởi giá trị đúng; nếu lỗi do phân tích mẫu hỏng thì kết quả phải để ở ô đúng của nó. Sau khi hiệu chỉnh như vậy, cần lặp lại việc kiểm tra phát hiện giá trị tản mạn hoặc giá trị bất thường. Nếu sự giải thích lỗi kỹ thuật chứng tỏ rằng không thể thay thế kết quả thử nghiệm sai thì nó cần được loại bỏ như một giá trị bất thường không hợp thức của thí nghiệm.
c) Khi giá trị tản mạn và/hoặc giá trị bất thường thống kê nào đó còn lại mà không được giải thích hoặc không bị loại bỏ vì thuộc phòng thí nghiệm bất thường, thì những giá trị tản mạn được giữ lại như là số đúng còn những giá trị bất thường thống kê sẽ bị loại bỏ trừ khi nhà thống kê quyết định giữ chúng lại vì lý do xác đáng.
d) Nếu số liệu cho ô bị từ chối đối với biểu mẫu B của hình 2 theo quy trình trên, thì số liệu tương ứng sẽ bị từ chối đối với biểu mẫu C của hình 2, và ngược lại
7.3.2.2. Các phép kiểm nghiệm đưa ra ở 7.3.3 và 7.3.4 có 2 loại. Phép kiểm nghiệm Cochran là phép thử sự biến động trong phạm vi phòng thí nghiệm và nên áp dụng trước tiên, sau đó mới tiến hành bất cứ hành động cần thiết nào với các phép thử lặp lại nếu cần. Phép kiểm nghiệm khác (Grubb’) chủ yếu là phép thử sự biến động giữa các phòng thí nghiệm, và nó cũng có thể được sử dụng (nếu n>2) khi phép kiểm nghiệm Cochran đã dẫn đến sự nghi ngờ rằng có sự thay đổi lớn trong phạm vi các phòng thí nghiệm hay đó chỉ là một trong các kết quả thử nghiệm trong ô đó.
7.3.3. Phép kiểm nghiệm Cochran
7.3.3.1 Tiêu chuẩn này giả thiết rằng giữa các phòng thí nghiệm chỉ có sự khác nhau nhỏ về phương sai trong phạm vi phòng thí nghiệm. Tuy nhiên, kinh nghiệm chỉ ra rằng không phải lúc nào cũng như vậy, phép kiểm nghiệm ở đây dùng để kiểm tra giả thiết đặt ra. Có thể sử dụng một số phép kiểm nghiệm cho mục đích này, nhưng ở đây phép kiểm nghiệm Cochran đã được chọn.
7.3.3.2. Cho trước một tập hợp p độ lệch chuẩn sj, chúng được tính toán từ một số lượng như nhau n kết quả lặp lại, sổ thống kê của phép kiểm nghiệm Cochran, C là:
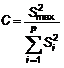 …….(8)
…….(8)
trong đó: Smax là độ lệch chuẩn lớn nhất trong tập hợp.
a) Nếu thống kê kiểm nghiệm nhỏ hơn hoặc bằng 5% giá trị tới hạn của nó thì hạng mục kiểm nghiệm được chấp nhận là đúng.
b) Nếu thống kê kiểm nghiệm lớn hơn 5% giá trị tới hạn và nhỏ hơn hoặc bằng 1% giá trị tới hạn của nó thì hạng mục kiểm nghiệm được gọi là giá trị tản mạn và được đánh dấu hoa thị đơn.
c) Nếu thống kê kiểm nghiệm lớn hơn 1% giá trị tới hạn của nó thì hạng mục kiểm nghiệm được gọi là giá trị bất thường thống kê và được đánh dấu hoa thị kép.
Các giá trị tới hạn đối với phép kiểm nghiệm Cochran cho trong 8.1 (bảng 4).
Phép kiểm nghiệm Cochran được áp dụng cho biểu mẫu C trong hình 2 ở từng mức riêng biệt.
7.3.3.3. Điều kiện Cochran chỉ áp dụng chặt chẽ khi tất cả các độ lệch chuẩn được suy ra từ cùng một số n các kết quả thử nghiệm thu được trong điều kiện lặp lại. Trong thực tế, số đó có thể thay đổi do số liệu thiếu hoặc bị loại bỏ. Tuy nhiên, tiêu chuẩn này giả thiết rằng trong một thí nghiệm được tổ chức tốt, những sự thay đổi như vậy về số lượng của các kết quả thử nghiệm ở từng ô sẽ được hạn chế và có thể bỏ qua, và do vậy điều kiện Cochran được áp dụng cho số kết quả thử nghiệm n sẽ xuất hiện trong phần lớn các ô.
7.3.3.4. Điều kiện Cochran chỉ kiểm tra giá trị cao nhất trong tập hợp các độ lệch chuẩn và do vậy nó là phép thử giá trị bất thường một phía. Tính không đồng nhất về phương sai cũng có thể phản ánh trong một số các độ lệch chuẩn tương đối nhỏ. Tuy vậy, giá trị nhỏ của độ lệch chuẩn có thể bị ảnh hưởng rất nhiều bởi mức độ làm tròn số liệu gốc và do đó chúng không đáng tin cậy hoàn toàn. Thêm vào đó, không có lý do để gạt bỏ số liệu khỏi phòng thí nghiệm vì độ chụm trong các kết quả thử nghiệm của nó cao hơn so với các phòng thí nghiệm khác. Do vậy điều kiện Cochran được coi là thỏa đáng.
7.3.3.5. Trong kiểm tra tới hạn ở biểu mẫu C trong hình 2 đôi khi phát hiện ra rằng tại một phòng thí nghiệm cá biệt độ lệch chuẩn ở tất cả hoặc ở hầu hết các mức thấp hơn so với các phòng thí nghiệm khác. Điều đó có thể chỉ ra rằng phòng thí nghiệm này làm việc với độ lệch chuẩn lặp lại thấp hơn so với phòng thí nghiệm khác. Nguyên nhân có thể do kỹ thuật và thiết bị tốt hơn hoặc do việc áp dụng đã có sự thay đổi đúng hoặc không đúng phương pháp đo tiêu chuẩn. Nếu điều này xảy ra phải thông báo cho hội đồng biết để sau đó quyết định xem nó có thích hợp với việc nghiên cứu chi tiết hơn không. (Ví dụ về điều này là phòng thí nghiệm 2 trong thí nghiệm được chi tiết hóa ở B.1)
7.3.3.6. Nếu độ lệch chuẩn lớn nhất được coi là giá trị bất thường thì giá trị ấy nên được bỏ qua và phép kiểm nghiệm Cochran được lặp lại trên các giá trị còn lại. Quá trình này có thể được lặp lại nhưng nó có thể dẫn đến những sự lược bỏ quá mức khi sự giả thiết cơ bản về phân bố chuẩn không được đáp ứng tốt. Áp dụng lặp lại phép kiểm nghiệm Cochran đề ra ở đây chỉ như phương tiện trợ giúp trong việc xem xét sự không đầy đủ của một phép thử thống kê được thiết kế để kiểm tra cùng một lúc một số giá trị bất thường. Phép kiểm nghiệm Cochran không được thiết kế cho mục đích này và phải rất thận trọng khi đưa ra các kết luận. Khi hai hoặc ba phòng thí nghiệm đưa ra các kết quả có độ lệch chuẩn lớn, đặc biệt nếu điều này xảy ra chỉ ở một mức, các kết luận từ phép kiểm nghiệm Cochran cần phải được kiểm tra cẩn thận. Mặt khác, nếu một số giá trị tản mạn và/hoặc giá trị bất thường thống kê được tìm thấy ở các mức khác nhau trong một phòng thí nghiệm, thì điều này có thể là một bằng chứng rõ ràng về sự quá bất thường của phương sai phòng thí nghiệm và tất cả các số liệu của phòng thí nghiệm đó cần phải loại bỏ.
7.3.4. Phép kiểm nghiệm Grubb
7.3.4.1. Một quan trắc bất thường
Cho tập hợp các số liệu xi với i = 1, 2, 3 …. p, được sắp xếp tăng dần. Sử dụng phép kiểm nghiệm Grubb để xác định xem giá trị quan trắc lớn nhất có là bất thường không tính số thống kê Grubb, Gp.
Gp = (xp – ![]() )/ s …..(9)
)/ s …..(9)
trong đó
![]() …….. (10)
…….. (10)
và
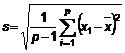 ……….. (11)
……….. (11)
Để kiểm tra ý nghĩa của giá trị quan trắc nhỏ nhất, tính thống kê kiểm nghiệm
Gp = (![]() – x1)/ s …..(9)
– x1)/ s …..(9)
a) Nếu số đó nhỏ hơn hoặc bằng 5% giá trị tới hạn của nó thì hạng mục thử được chấp nhận là đúng
b) Nếu số đó lớn hơn 5% giá trị tới hạn của nó và nhỏ hơn hoặc bằng 1% giá trị tới hạn của nó thì hạng mục thử được gọi là giá trị tản mạn và được đánh dấu hoa thị đơn.
c) Nếu số đó lớn hơn 1% giá trị tới hạn của nó thì hạng mục thử được gọi là giá trị bất thường thống kê và được đánh dấu hoa thị kép.
7.3.4.2. Hai quan trắc bất thường
Để kiểm tra xem hai giá trị quan trắc lớn nhất có thể là bất thường không, tính số thống kê của phép kiểm nghiệm Grubb G:
![]() …….(12)
…….(12)
trong đó
![]() …..…..(13)
…..…..(13)
và
![]() ……….(14)
……….(14)
và
![]() ……….(15)
……….(15)
Hoặc là để kiểm tra hai giá trị quan trắc nhỏ nhất, tính số thống kê của phép kiểm nghiệm Grubb G:
![]() ……… (16)
……… (16)
trong đó
![]() ……….. (17)
……….. (17)
và
![]() ………… (18)
………… (18)
Các giá trị tới hạn của phép kiểm nghiệm Grubb cho trong 8.2 (bảng 5).
7.3.4.3. Áp dụng của phép kiểm nghiệm Grubb
Khi phân tích thí nghiệm độ chụm, phép kiểm nghiệm Grubb có thể được áp dụng cho các trường hợp sau:
a) Các trung bình ô (mẫu B hình 2) ở mức j đã cho, trong trường hợp đó
![]()
và
p = pj
trong đó j là cố định.
Lấy các số liệu ở một mức, áp dụng phép kiểm nghiệm Grubb cho một quan trắc bất thường đối với các giá trị trung bình ô như mô tả ở 7.3.4.1 . Nếu theo phép thử này trung bình ô là giá trị bất thường thì loại bỏ và lặp lại phép thử ở giá trị trung bình ô cực trị khác (ví dụ nếu giá trị lớn nhất là giá trị bất thường thì xem xét giá trị nhỏ nhất sau khi giá trị lớn nhất đã bị loại bỏ), nhưng không áp dụng phép kiểm nghiệm Grubb cho hai quan trắc bất thường mô tả ở 7.3.4.2. Nếu phép kiểm nghiệm Grubb không chỉ ra trung bình ô là bất thường thì áp dụng phép kiểm nghiệm Grubb kép mô tả ở 7.3.4.2.
b) Kết quả đơn trong một ô, khi phép kiểm nghiệm Cochran chỉ ra độ lệch chuẩn ô là nghi ngờ.
7.4. Tính trung bình chung và phương sai
7.4.1. Phương pháp phân tích
Phương pháp phân tích trong tiêu chuẩn này bao gồm việc ước lượng m và độ chụm cho từng mức riêng biệt. Các kết quả được thể hiện trong bảng cho từng giá trị j.
7.4.2. Số liệu cơ sở
Các số liệu cơ sở cần thiết cho việc tính toán được trình bày trong ba bảng ở hình 2:
– Bảng A gồm các kết quả thử nghiệm gốc.
– Bảng B gồm các giá trị trung bình ô;
– Bảng C gồm các thước đo sự phân tán trong phạm vi ô.
7.4.3. Các ô không rỗng
Theo qui tắc đưa ra trong 7.3.2.1 d), vói một mức cụ thể, số ô không rỗng sử dụng trong tính toán sẽ luôn luôn giống nhau trong các bảng B và C. Ngoại lệ có thể xảy ra do thiếu số liệu, nếu một ô trong bảng A chỉ chứa một kết quả thử nghiệm đơn và kéo theo một ô rỗng trong bảng C nhưng không kéo theo ô rỗng trong bảng B. Trong trường hợp đó có thể:
a) Loại bỏ kết quả thử nghiệm đơn lẻ dẫn đến ô trống trong cả hai bảng B và C, hoặc
b) Gạch ngang trong bảng C nếu coi điều này là một sự mất mát không đáng kể.
Số lượng các ô không rỗng có thể khác nhau ở các mức khác nhau, do đó phải có chỉ số j trong pi.
7.4.4. Tính trung bình tổng thể ![]()
Đối với mức j, trung bình tổng thể là
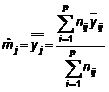 ……(19)
……(19)
7.4.5. Tính các phương sai
Ba phương sai được tính cho mỗi mức là phương sai lặp lại, phương sai giữa các phòng thí nghiệm và phương sai tái lập.
7.4.5.1. Phương sai lặp lại
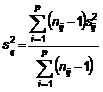 …… (20)
…… (20)
7.4.5.2. Phương sai giữa các phòng thí nghiệm
![]() ……. (21)
……. (21)
trong đó
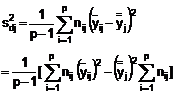 …….. (22)
…….. (22)
và
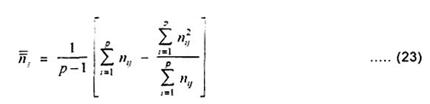
Các phép tính này được minh hoạ bằng các ví dụ B.1 và B.3 ở phụ lục B.
7.4.5.3. Đối với trường hợp đặc biệt khi tất cả nij = n = 2, có thể sử dụng công thức đơn giản hơn, như
![]()
và
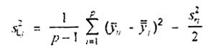
Chúng được minh hoạ bằng ví dụ trong B.2.
7.4.5.4. Khi SLj2 có giá trị âm từ các phép tính trên do các tác động ngẫu nhiên thì giá trị đó nên được giả thiết bằng không
7.4.5.5. Phương sai tái lập bằng
![]() ……(24)
……(24)
7.4.6. Sự phụ thuộc của các phương sai vào m
Cần tìm hiểu xem độ chụm có phụ thuộc m hay không và nếu có thì cần xác định mối quan hệ hàm số này.
7.5. Thiết lập mối quan hệ hàm số giữa các giá trị độ chụm và mức trung bình m
7.5.1. Không thể lúc nào cũng tồn tại mối quan hệ hàm số chính qui giữa độ chụm và m . Đặc biệt, khi sự không đồng nhất của vật liệu gắn với sự thay đổi của các kết quả thử nghiệm, thì sẽ chỉ có mối quan hệ hàm số nếu sự không đồng nhất của vật liệu là hàm số chính tắc của mức m. Với các vật liệu rắn có các thành phần khác nhau và nhận được từ các quá trình sản xuất khác nhau thì mối quan hệ hàm số chính tắc là không thể rõ ràng. Điều này cần được quyết định trước khi áp dụng quy trình tiếp sau. Hoặc sẽ phải thiết lập các giá trị riêng biệt của độ chụm cho từng vật liệu được nghiên cứu.
7.5.2. Các quy trình lập luận và tính toán trình bày ở 7.5.3 đến 7.5.9 áp dụng cả cho độ lệch chuẩn lặp lại và tái lập. Để ngắn gọn ở đây chỉ trình bày cho độ lệch chuẩn lặp lại. Sẽ chỉ xét ba loại quan hệ:
I: sr = bm (đường thẳng qua điểm gốc)
II: sr = a + bm (đường thẳng với điểm chặn dương)
III: lg sr = c + d Ig m (hoặc sr = C md); d ≤ 1 (mối quan hệ luỹ thừa)
Hy vọng ít nhất là một trong các công thức trên có được sự phù hợp thỏa đáng trong đa số các trường hợp. Nếu không, nhà thống kê tiến hành việc phân tích cần có giải pháp thay thế. Để tránh nhầm lẫn, các hằng số a, b, c, C và d xuất hiện trong các phương trình đó có thể được phân biệt bằng các chỉ số dưới, ar, br…. cho độ lặp lại và aR; bR ….. cho độ tái lập, để đơn giản hóa các ký hiệu trong mục này các chỉ số đó được bỏ qua. Kí hiệu sr cũng được viết tắt là s để dành một tiếp hậu tổ cho mức j.
7.5.3. Thông thường d > 0 vì thế các mối quan hệ I và III sẽ dẫn đến s = 0 với m = 0, điều đó dường như không chấp nhận được từ góc độ thực nghiệm. Tuy nhiên, khi báo cáo các số liệu độ chụm cần làm rõ rằng chúng chỉ áp dụng trong phạm vi các mức được phủ bởi thí nghiệm độ chụm liên phòng.
7.5.4. Với a = 0 và d = 1, tất cả ba mối quan hệ là như nhau. Vì vậy khi a nằm gần không và/hoặc d nằm gần một thì hai hoặc cả ba mối quan hệ này thực tế sẽ mang lại sự phù hợp tương đương nhau. Trong trường hợp đó mối quan hệ I cần được ưu tiên vì nó cho phép có được nhận định đơn giản sau đây:
“Hai kết quả thử nghiệm được coi là nghi ngờ khi chúng khác nhau hơn (100 b)% “
Theo thuật ngữ thống kê: đó là điều khẳng định rằng hệ số thay đổi (100 s/m) là không đổi ở tất cả các mức.
7.5.5. Nếu trên đồ thị của sj đối với ![]() , hoặc đồ thị của Ig sj đối với Ig
, hoặc đồ thị của Ig sj đối với Ig ![]() , tập hợp các điểm được tìm thấy nằm tương đối gần một đường thẳng thì một đường vẽ bằng tay có thể đưa ra lời giải thỏa đáng; nhưng nếu vì lý do nào đó mà phương pháp làm khớp bằng số được ưu tiên thì quy trình trong 7.5.6 được khuyến nghị dùng cho dạng quan hệ I và II và quy trình trong 7.5.8 cho dạng quan hệ III.
, tập hợp các điểm được tìm thấy nằm tương đối gần một đường thẳng thì một đường vẽ bằng tay có thể đưa ra lời giải thỏa đáng; nhưng nếu vì lý do nào đó mà phương pháp làm khớp bằng số được ưu tiên thì quy trình trong 7.5.6 được khuyến nghị dùng cho dạng quan hệ I và II và quy trình trong 7.5.8 cho dạng quan hệ III.
7.5.6. Nhìn từ góc độ thống kê, sự khớp với một đường thẳng là rất phức tạp bởi trên thực tế cả ![]() và sj đều là ước lượng và do vậy gắn với sai số. Nhưng độ dốc b thường nhỏ (mức 0,1 hoặc nhỏ hơn), vì thế những sai số trong
và sj đều là ước lượng và do vậy gắn với sai số. Nhưng độ dốc b thường nhỏ (mức 0,1 hoặc nhỏ hơn), vì thế những sai số trong ![]() m có ảnh hưởng nhỏ và những sai số trong ước lượng s chiếm ưu thế.
m có ảnh hưởng nhỏ và những sai số trong ước lượng s chiếm ưu thế.
7.5.6.1. Việc ước lượng tốt các tham số của đường hồi quy yêu cầu một phép hồi quy có trọng số bởi vì sai số tiêu chuẩn của s tỷ lệ thuận với giá trị dự đoán của sj (![]() ).
).
Các trọng số phải tỷ lệ thuận với 1/(![]() )2: trong đó
)2: trong đó ![]() là độ lệch chuẩn lặp lại dự đoán trước đối với mức j. Tuy nhiên
là độ lệch chuẩn lặp lại dự đoán trước đối với mức j. Tuy nhiên ![]() phụ thuộc các tham số sẽ phải tính.
phụ thuộc các tham số sẽ phải tính.
Quy trình toán học chính xác để tìm ước lượng theo phương pháp bình phương nhỏ nhất có trọng số của các số dư có thể phức tạp. Quy trình khuyến nghị dưới đây đã được chứng minh là thỏa đáng trong thực tế.
7.5.6.2. Với trọng số Wj bằng 1/(![]() )2, trong đó N = 0,1,2 ……… đối với những sự lặp lại liên tiếp, thì các công thức tính như sau:
)2, trong đó N = 0,1,2 ……… đối với những sự lặp lại liên tiếp, thì các công thức tính như sau:
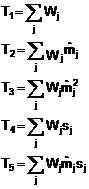
Đối với dạng quan hệ I (s = bm), giá trị của b được cho bằng T5/T3.
Đối với dạng quan hệ II (s = a + bm):
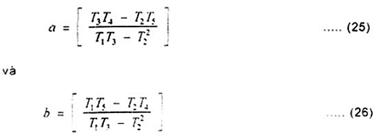
7 5.6.3. Đối với dạng quan hệ I, phép thế đại số cho các trọng số Wj =1/(![]() )2 bằng
)2 bằng ![]() = b
= b![]() , bm dẫn đến cách thể hiện đơn giản sau:
, bm dẫn đến cách thể hiện đơn giản sau:
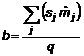 …… (27)
…… (27)
và không cần tiếp tục gì nữa.
7.5.6.4. Đối với dạng quan hệ II, các giá trị ban đầu ![]() , là các giá trị gốc của s nhận được bằng các quy trình ở 7.4. Chúng được dùng để tính
, là các giá trị gốc của s nhận được bằng các quy trình ở 7.4. Chúng được dùng để tính
W0j = l ![]() (j = 1, 2, …., q)
(j = 1, 2, …., q)
và để tính a1, và b1. theo mục 7.5.6.2.
Điều này dẫn đến
![]()
Các phép tính được lặp lại với W1j= 1/(![]() )2 để có:
)2 để có:
![]()
Quy trình tương tự có thể được lặp lại một lần nữa với trọng số W2j = 1 /(![]() )2 suy ra từ những phương trình đó, nhưng điều này sẽ chỉ dẫn đến những thay đổi không quan trọng. Bước từ W01 đến W1j có tác dụng trong việc loại trừ những sai số thô của các trọng số, và các phương trình cho
)2 suy ra từ những phương trình đó, nhưng điều này sẽ chỉ dẫn đến những thay đổi không quan trọng. Bước từ W01 đến W1j có tác dụng trong việc loại trừ những sai số thô của các trọng số, và các phương trình cho ![]() , nên được coi là kết quả cuối cùng.
, nên được coi là kết quả cuối cùng.
7.5.7. Sai số tiêu chuẩn của Ig s không phụ thuộc vào s và như vậy một phép hồi quy không trọng số của Ig s đối với Ig ![]() là thích hợp.
là thích hợp.
7.5.8. Đối với dạng quan hệ III, các công thức tính như sau:
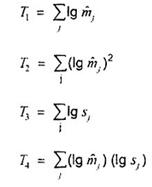
và từ đó

và

7.5.9. Ví dụ về các mối quan hệ phù hợp I, II, III của 7.5.2 đối với tập hợp số liệu giống nhau được đưa ra trong 7.5.9.1 đến 7.5.9.3. Các số liệu được lấy từ tình huống nghiên cứu trong B.3 và được sử dụng ở đây chỉ để minh họa quy trình. Nó sẽ được thảo luận thêm ở B.3.
7.5.9.1. Ví dụ về mối quan hệ phù hợp I cho ở bảng 1.
7.5.9.2 Ví dụ về mối quan hệ phù hợp II cho ở bảng 2 (![]() .sj như trong 7.5.9.1).
.sj như trong 7.5.9.1).
7.5.9.3. Ví dụ về mối quan hệ phù hợp III cho ở bảng 3.
Bảng 1 – Quan hệ I: s – bm
|
sj |
3.94 0.092 |
8.28 0.179 |
14.18 0.127 |
15,59 0.337 |
20.41 0.393 |
|
sj / |
0.023 4 |
0.021 6 |
0.008 9 |
0.021 6 |
0.019 3 |
|
|
|
||||
|
s = bm |
0,075 |
0,157 |
0,269 |
0,296 |
0,388 |
Bảng 2 – Quan hệ II: s = a – bm
|
w0j |
118 |
31 |
62 |
8.8 |
6.5 |
|
S1 = 0,058 + 0,009 0 m |
|||||
|
|
0,09 116 |
0,132 57 |
0,185 29 |
0,197 26 |
0,240 17 |
|
S2 = 0,030 + 0,015 6 m |
|||||
|
|
0,092 118 |
0,159 40 |
0,251 16 |
0,273 13 |
0,348 8 |
|
S3 = 0,032 + 0,015 4 m |
|||||
|
|
0,093 |
0,160 |
0,251 |
0,273 |
0,348 |
|
Chú thích – Giá trị của các trọng số không phải là giá trị tới hạn: Hai số có nghĩa là đủ |
|||||
|
1) Sai lệch so với s2 không đáng kể |
|||||
Bảng 3 – Quan hệ III: Ig s = c – d Ig bm
|
|
+ 0,595 – 1.036 |
+ 0,918 – 0,747 |
+ 1,152 – 0,896 |
+ 1,193 – 0,472 |
+ 1,310 – 0,406 |
|
lg s = 1,506 6 – 0,7 72 Ig m hoặc s = 0,031 m 0,77 |
|||||
|
s |
0,089 |
0,158 |
0,239 |
0,257 |
0,316 |
7.6. Phân tích thống kê theo quy trình từng bước
Chú thích 5 – Hình 3 trình bày quy trình cho trong 7.6 theo cách làm từng bước
7.6.1. Thu thập tất cả kết quả thử nghiệm có được trong một biểu mẫu, biểu mẫu A ở hình 2 (xem 7.2). Nên sắp xếp biểu mẫu này thành p hàng, với chỉ số i = 1, 2, 3, …… p (đại diện cho p phòng thí nghiệm có số liệu) và q cột, với chỉ số j = 1, 2 …….. q (đại diện cho q mức theo thứ tự tăng dần).
Trong thí nghiệm đồng mức các kết quả thử nghiệm trong phạm vi một ô của biểu mẫu A không cần thiết phải phân biệt rõ và có thể sắp xếp theo bất kỳ thứ tự nào.
7.6.2. Kiểm tra biểu mẫu A đối với bất kỳ sự không bình thường dễ nhận thấy nào, phát hiện nếu cần thiết, loại bỏ mọi số liệu rõ ràng là sai (ví dụ, số liệu nằm ngoài phạm vi đo của phương tiện đo hoặc số liệu không thể chấp nhận vì lý do kỹ thuật) và thông báo đến hội đồng. Đôi khi đây là bằng chứng trực tiếp về các kết quả thử nghiệm của một phòng thí nghiệm cụ thể hoặc trong một ô cụ thể tại một mức là không nhất quán với các số liệu khác. Phải loại bỏ ngay những số liệu rõ ràng không hoà hợp như vậy. Phải thông báo cho hội đồng việc loại bỏ này để xem xét sau này (xem 7.7.1).
7.6.3. Từ biểu mẫu A, đã được hiệu chỉnh theo 7.6.2, tính biểu mẫu B chứa các trung bình ô và biểu mẫu C chứa các thước đo của sự phân tán trong phạm vi ô.
Khi ô ở biểu mẫu A chỉ chứa kết quả thử nghiệm đơn, một trong các sự lựa chọn của 7.4.3 cần được chấp nhận.
7.6.4. Chuẩn bị các đồ thị Mandel h và k như mô tả ở 7.3.1 và kiểm tra chúng về sự phù hợp với số liệu. Những đồ thị đó có thể chỉ ra sự thích hợp của số liệu đối với sự phân tích tiếp theo, những giá trị hoăc những phòng thí nghiệm không phù hợp. Tuy nhiên, không có quyết định cuối cùng nào được đưa ra ở bước này, nó chỉ được đưa ra khi kết thúc 7.6.5 đến 7.6.9.
7.6.5. Kiểm tra từng mức của các biểu mẫu B và C (xem hình 2) để tìm các giá trị tản mạn và/hoặc các giá trị bất thường thống kê [xem 7.3.2.1 a)]. Áp dụng các phép thử thống kê trong 7.3 đối với tất cả các hạng mục nghi ngờ, đánh dấu giá trị tản mạn bằng hoa thị đơn và giá trị bất thường bằng hoa thị kép. Nếu không có các giá trị tản mạn hoặc giá trị bất thường thống kê, bỏ qua các bước 7.6.6 đến 7.6.10 để thực hiện 7.6.11.
7.6.6. Phát hiện xem có thể có sự lý giải kỹ thuật nào cho các giá trị tản mạn và/hoặc giá trị bất thường thống kê không, và nếu có thể, xác nhận sự lý giải như vậy. Hiệu chỉnh hoặc loại bỏ theo yêu cầu những giá trị tản mạn và/hoặc giá trị bất thường thống kê đã được lý giải thỏa đáng, và áp dụng các hiệu chính tương ứng cho các biểu mẫu đó. Nếu tất cả các giá trị tản mạn hoặc giá trị bất thường thống kê đã được lý giải, bỏ qua các bước 7.6.7 đến 7.6.10 để thực hiện 7.6.11.
Chú thích 6 – Số lượng lớn các giá trị tản mạn và/hoặc giá trị bất thường có thể chỉ ra sự không đồng nhất của phương sai hoặc các chênh lệch được tuyên bố giữa các phòng thí nghiệm và như vậy có thể tạo ra nghi ngờ về sự thích hợp của phương pháp đo. Điều này phải được thông báo cho hội đồng.
7.6.7. Nếu sự phân bố của các giá trị tản mạn hoặc các giá trị bất thường (chưa được lý giải trong biểu mẫu B và C) không đưa ra bất cứ phòng thí nghiệm không phù hợp nào (xem 7.2.5), thì bỏ qua 7.6.8 để thực hiện 7.6.9.
7.6.8. Nếu bằng chứng về một số phòng thí nghiệm bị nghi ngờ là không phù hợp đủ mạnh để quyết định loại bỏ một số hoặc tất cả các số liệu từ các phòng thí nghiệm đó thì loại bỏ các số liệu cần thiết và thông báo cho hội đồng.
Quyết định loại bỏ một số hay tất cả số liệu từ một phòng thí nghiệm cụ thể nào đó là trách nhiệm của chuyên gia thống kê thực hiện phân tích. Việc loại bỏ này phải được thông báo cho hội đồng để xem xét sau này (xem 7.7.1).
7.6.9. Nếu giá trị tản mạn và/hoặc giá trị bất thường thống kê nào đó còn lại mà chưa được lý giải hoặc được xem là của phòng thí nghiệm bất thường thì loại bỏ giá trị bất thường thống kê nhưng giữ lại giá trị tản mạn.
7.6.10. Bất kỳ việc nhập số liệu nào đó trong biểu mẫu B nếu đã bị bị loại bỏ ở các bước trước đây thì việc nhập số liệu tương ứng trong C cũng bị loại bỏ và ngược lại.
7.6.11. Tính mức trung bình ![]() , các độ lệch chuẩn lặp lại và tái lập đối với từng mức riêng biệt từ những số liệu giữ lại được coi là đúng trong các biểu mẫu B và C theo các quy trình đưa ra ở mục 7.4.
, các độ lệch chuẩn lặp lại và tái lập đối với từng mức riêng biệt từ những số liệu giữ lại được coi là đúng trong các biểu mẫu B và C theo các quy trình đưa ra ở mục 7.4.
7.6.12. Nếu thí nghiệm chỉ sử dụng mức đơn hoặc nếu đã quyết định phải cho biết độ lệch chuẩn lặp lại và tái lập riêng rẽ đối với từng mức (xem 7.5.1) và không là các hàm số của mức thì bỏ qua các bước 7.6.13 đến 7.6.18 để thực hiện 7.6.19.
Chú thích 7 – Các bước 7.6.13 đến 7.6.17 được áp dụng riêng biệt cho sr. và sR, nhưng để ngắn gọn chỉ trình bày chúng cho sr.
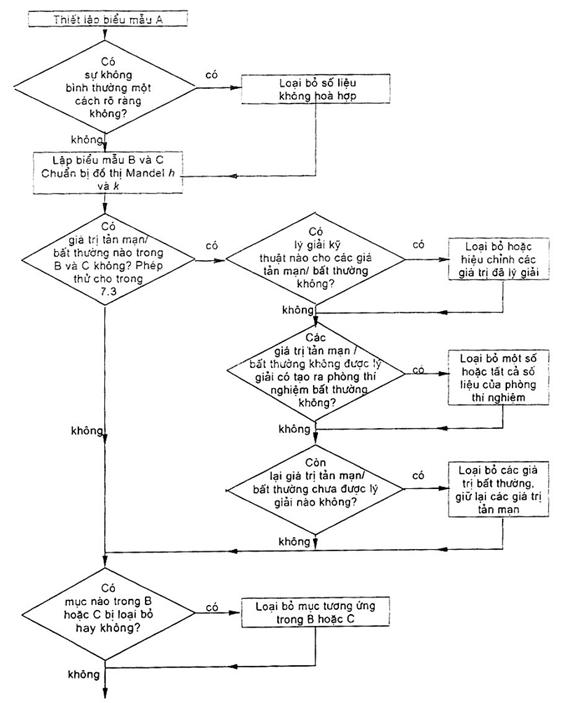
Hình 3 – Sơ đồ chỉ dẫn các bước cơ bản trong phân tích thống kê
(phần tiếp theo ở trang sau)
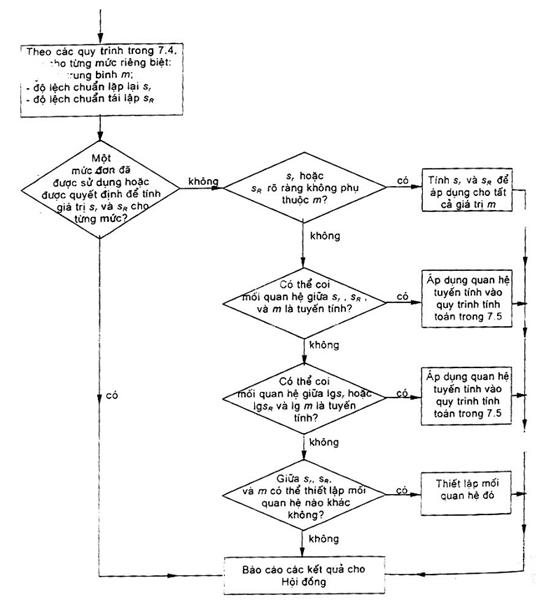
Hình 3 – Sơ đồ chỉ dẫn các bước cơ bản trong phân tích thống kê
7.6.13. Lặp đồ thị sj theo ![]() và dựa vào đồ thị này đánh giá xem s có pnụ thuộc vào m hay không. Nếu s được coi là phụ thuộc vào m thì bỏ qua bước 7.6.14 và thực hiện 7.6.15. Nếu s được coi là không phụ thuộc m, thì thực hiện theo 7.6.14. Nếu có nghi ngờ, tốt nhất là đưa ra cả hai trường hợp để hội đồng quyết định. Không có phép thử thống kê thích hợp cho vấn đề này. nhưng chuyên gia kỹ thuật về phương pháp đo cần có kinh nghiệm để đưa ra quyết định.
và dựa vào đồ thị này đánh giá xem s có pnụ thuộc vào m hay không. Nếu s được coi là phụ thuộc vào m thì bỏ qua bước 7.6.14 và thực hiện 7.6.15. Nếu s được coi là không phụ thuộc m, thì thực hiện theo 7.6.14. Nếu có nghi ngờ, tốt nhất là đưa ra cả hai trường hợp để hội đồng quyết định. Không có phép thử thống kê thích hợp cho vấn đề này. nhưng chuyên gia kỹ thuật về phương pháp đo cần có kinh nghiệm để đưa ra quyết định.
7.6.14. Sử dụng 1/q = S Sj = Sr làm giá trị cuối cùng của độ lệch chuẩn lặp lại. Bỏ qua các bước 7.6.15 đến 7.6.18 để thực hiện 7.6.19.
7.6.15. Theo đồ thị trong 7.6.13 đánh giá xem có thể biểu diễn mối quan hệ giữa s và m bằng đường thẳng hay không và nếu thế thì mối quan hệ I (s = bm) hay II (s = a + bm) có thích hợp không (xem 7.5.2). Xác định tham số b hoặc hai tham số a và b bằng quy trình 7.5.6. Nếu mối quan hệ tuyến tính được coi là thoả đáng thì bỏ qua bước 7.6.16 để thực hiện 7.6.17. Nếu không, tiến hành 7.6.16.
7.6.16. Lập đồ thị Ig sj theo Ig![]() và dựa vào đồ thị này đánh giá xem mối quan hệ giữa Ig s và Ig m có thể thể hiện hợp lý bằng một đường thẳng hay không. Nếu điều này được xem là thỏa đáng thì lập mối quan hệ III (Ig s = c + d Ig m) bằng quy trình trình bày trong 7.5.8.
và dựa vào đồ thị này đánh giá xem mối quan hệ giữa Ig s và Ig m có thể thể hiện hợp lý bằng một đường thẳng hay không. Nếu điều này được xem là thỏa đáng thì lập mối quan hệ III (Ig s = c + d Ig m) bằng quy trình trình bày trong 7.5.8.
7.6.17. Nếu mối quan hệ thỏa đáng được thiết lập ở các bước 7.6.15 hoặc 7.6.16 thì giá trị cuối cùng của sr (hoặc sR) là các giá trị nhận được từ mối quan hệ đó với các giá trị đã cho của m. Bỏ qua bước 7.6.18 để thực hiện 7.6.19.
7.6.18. Nếu không có mối quan hệ thỏa đáng nào được thiết lập ở bước 7.6.15 hoặc 7.6.16 thì chuyên gia thống kê cần quyết định xem có thể thiết lập một vài mối quan hệ khác giữa s và m hay không hoặc là không thể thiết lập mối quan hệ hàm số được từ những số liệu bất thường như vậy.
7.6.19. Chuẩn bị báo cáo đưa ra số liệu cơ bản và các kết quả cùng kết luận rút ra từ phân tích thống kê và trình hội đồng. Sự trình bày bằng đồ thị ở 7.3.1 có thể được sử dụng để thể hiện sự nhất quán hoặc sự thay đổi của các kết quả.
7.7. Báo cáo trình hội đồng và các quyết định của hội đồng
7.7.1. Báo cáo của chuyên gia thống kê
Sau khi kết thúc việc phân tích thống kê, chuyên gia thống kê cần viết báo cáo để trình hội đồng. Trong báo cáo đó những thông tin sau phải được đưa ra:
a) Báo cáo đầy đủ về các quan trắc nhận được từ thao tác viên và/hoặc các giám sát viên liên quan đến tiêu chuẩn về phương pháp đo.
b) Báo cáo đầy đủ về các phòng thí nghiệm bị loại bỏ vì không phù hợp trong các bước 7.6.2 và 7.6.8 cùng với các lý do của việc loại bỏ này;
c) Báo cáo đầy đủ về các giá trị tản mạn và/hoặc giá trị bất thường thống kê đã được phát hiện: chúng đã được lý giải, hiệu chỉnh hoặc loại bỏ hay chưa:
d) Biểu mẫu của các kết quả cuối cùng ![]() , sr , sR và một báo cáo về các kết luận thu được trong các bước 7.6.13, 7.6.15 hoặc 7.6.16, minh hoạ bằng một trong các đồ thị được khuyến nghị tại bước đó;
, sr , sR và một báo cáo về các kết luận thu được trong các bước 7.6.13, 7.6.15 hoặc 7.6.16, minh hoạ bằng một trong các đồ thị được khuyến nghị tại bước đó;
e) Một phụ lục là các biểu mẫu A, B và C (hình 2) đã được sử dụng trong phân tích thống kê.
7.7.2. Các quyết định của hội đồng
Hội đồng thảo luận báo cáo trên và đưa ra các quyết định liên quan đến các vấn đề sau:
a) Các kết quả thử nghiệm không phù hợp, các giá trị tản mạn hoặc bất thường (nếu có) là do sai sót trong việc trình bày của tiêu chuẩn về phương pháp đo?
b) Các hành động gì cần tiến hành đối với các phòng thí nghiệm bất thường bị loại bỏ?
c) Kết quả của các phòng thí nghiệm bất thường và/hoặc nhận xét của các thao tác viên và người giám sát có chỉ ra sự cần thiết phải cải tiến tiêu chuẩn về phương pháp đo không? Nếu có thì yêu cầu đối với sự cải tiến là gì?
d) Các kết quả của thí nghiệm độ chụm có làm rõ các giá trị của độ lệch chuẩn lặp lại và tái lập không? Nếu có thì đó là những giá trị nào, chúng cần được công bố theo hình thức và phạm vi nào?
7.7.3. Báo cáo đầy đủ
Người điều hành cần dự thảo một báo cáo nêu lên các lý do đối với công việc và việc tổ chức công việc như thế nào để trình hội đồng thông qua. Báo cáo này bao gồm báo cáo của chuyên gia thống kê và đưa ra những kết luận đã được thảo luận. Nên sử dụng sơ đồ về sự nhất quán hoặc thay đổi dùng để trình bày. Báo cáo cần được chuyển đến những nơi có trách nhiệm đối với công việc và những bên có quan tâm.
8. Các bảng thống kê
8.1. Các giá trị tới hạn đối với phép kiểm nghiệm Cochran (xem 7.3.3) cho trong bảng 4
Bảng 4 – Các giá trị tới hạn của phép kiêm nghiệm Cochran
|
p |
n = 2 |
n = 3 |
n = 4 |
n = 5 |
n = 6 |
|||||
|
1 % |
5 % |
1 % |
5% |
1 % |
5 % |
1 % |
5 % |
1 % |
5 % |
|
|
2 |
— |
— |
0,995 |
0,975 |
0,979 |
0,939 |
0,959 |
0,906 |
0,937 |
0,877 |
|
3 |
0,993 |
0,967 |
0,942 |
0,871 |
0,883 |
0,798 |
0,834 |
0 746 |
0793 |
0,707 |
|
4 |
0,968 |
0,906 |
0,864 |
0,768 |
0,781 |
0,684 |
0,721 |
0,629 |
0,676 |
0,590 |
|
5 |
0,928 |
0,841 |
0,788 |
0,684 |
0,696 |
0,598 |
0,633 |
0,544 |
0,588 |
0,506 |
|
6 |
0,883 |
0,781 |
0,722 |
0,616 |
0,626 |
0 532 |
0,564 |
0,480 |
0,520 |
0,445 |
|
7 |
0,838 |
0,727 |
0,664 |
0,561 |
0,563 |
0,480 |
0,508 |
0,431 |
0,466 |
0,397 |
|
8 |
0,794 |
0,680 |
0,615 |
0,516 |
0,521 |
0,438 |
0,463 |
0,391 |
0,423 |
0,360 |
|
9 |
0,754 |
0,638 |
0,573 |
0,478 |
0,481 |
0,403 |
0,425 |
0,358 |
0,387 |
0,329 |
|
10 |
0,718 |
0,602 |
0,536 |
0,445 |
0,447 |
0,373 |
0,393 |
0,331 |
0,357 |
0,303 |
|
11 |
0,684 |
0.570 |
0,504 |
0,417 |
0,418 |
0,248 |
0,366 |
0,308 |
0,332 |
0,281 |
|
12 |
0,653 |
0,541 |
0,475 |
0,392 |
0,392 |
0,326 |
0,343 |
0,288 |
0,310 |
0,262 |
|
13 |
0,624 |
0,515 |
0,450 |
0,371 |
0,369 |
0,307 |
0,322 |
0,271 |
0,291 |
0,243 |
|
14 |
0,599 |
0,492 |
0,427 |
0,352 |
0,349 |
0,291 |
0,304 |
0,255 |
0,274 |
0,232 |
|
15 |
0,575 |
0,471 |
0,407 |
0,335 |
0,332 |
0,276 |
0,288 |
0,242 |
0,259 |
0,220 |
|
16 |
0,553 |
0,452 |
0,388 |
0,319 |
0,316 |
0,262 |
0,274 |
0,230 |
0,246 |
0,208 |
|
17 |
0,532 |
0,434 |
0,372 |
0,305 |
0,301 |
0,250 |
0,261 |
0,219 |
0,234 |
0,198 |
|
18 |
0,514 |
0,418 |
0,356 |
0,293 |
0,288 |
0,240 |
0,249 |
0,209 |
0,223 |
0,189 |
|
19 |
0,496 |
0,403 |
0,343 |
0,281 |
0,276 |
0,230 |
0,238 |
0,200 |
0,214 |
0,181 |
|
20 |
0,480 |
0,389 |
0,330 |
0,270 |
0,265 |
0,220 |
0,229 |
0,192 |
0,205 |
0,174 |
|
21 |
0,465 |
0.377 |
0,318 |
0,261 |
0,255 |
0,212 |
0,220 |
0,185 |
0,197 |
0,167 |
|
22 |
0,450 |
0,365 |
0,307 |
0,252 |
0,246 |
0,204 |
0,212 |
0,178 |
0,189 |
0,160 |
|
23 |
0,437 |
0,354 |
0,297 |
0,243 |
0,238 |
0,197 |
0,204 |
0,172 |
0,182 |
0,155 |
|
24 |
0,425 |
0,343 |
0.287 |
0,235 |
0,230 |
0.191 |
0.197 |
0,166 |
0,176 |
0,149 |
|
25 |
0413 |
0,334 |
0,278 |
0,228 |
0,222 |
0,185 |
0,190 |
0,160 |
0,170 |
0,144 |
|
26 |
0,402 |
0,325 |
0,270 |
0,221 |
0,215 |
0,179 |
0,184 |
0,155 |
0,164 |
0,140 |
|
27 |
0,391 |
0,316 |
0,262 |
0,215 |
0,209 |
0,173 |
0,179 |
0,150 |
0,159 |
0,135 |
|
28 |
0,382 |
0,308 |
0,255 |
0,209 |
0,202 |
0,168 |
0,173 |
0 146 |
0,154 |
0,131 |
|
29 |
0,372 |
0,300 |
0,248 |
0,203 |
0,196 |
0,164 |
0,168 |
0,142 |
0,150 |
0,127 |
|
30 |
0,363 |
0,293 |
0,241 |
0,198 |
0,191 |
0,159 |
0,164 |
0,138 |
0,145 |
0,124 |
|
31 |
0,355 |
0,286 |
0,235 |
0,193 |
0,186 |
0,155 |
0,159 |
0,134 |
0,141 |
0,120 |
|
32 |
0,347 |
0,290 |
0,229 |
0,188 |
0,181 |
0,151 |
0,155 |
0,131 |
0,138 |
0,117 |
|
33 |
0,339 |
0,273 |
0,224 |
0,184 |
0,177 |
0,147 |
0,151 |
0,127 |
0,134 |
0,114 |
|
34 |
0,332 |
0,267 |
0,218 |
0,179 |
0,172 |
0,144 |
0,147 |
0,124 |
0,131 |
0,111 |
|
35 |
0,325 |
0,262 |
0,213 |
0,175 |
0,168 |
0,140 |
0,144 |
0,121 |
0,127 |
0,108 |
|
36 |
0,318 |
0,256 |
0,208 |
0,172 |
0,165 |
0,137 |
0,140 |
0,118 |
0,124 |
0,106 |
|
37 |
0,312 |
0,251 |
0,204 |
0,168 |
0,161 |
0,134 |
0,137 |
0,116 |
0,121 |
0,103 |
|
38 |
0,306 |
0,246 |
0,200 |
0,164 |
0,157 |
0,131 |
0,134 |
0,113 |
0,119 |
0,101 |
|
39 |
0,300 |
0,242 |
0,196 |
0,161 |
0,154 |
0,129 |
0,131 |
0,111 |
0,116 |
0,099 |
|
40 |
0,294 |
0,237 |
0,192 |
0,158 |
0,151 |
0,126 |
0,128 |
0,108 |
0,114 |
0,097 |
|
p = số phòng thí nghiệm ở mức đã cho n = số kết quả thử nghiệm trong ô |
||||||||||
8.2. Các giá trị tới hạn đối với phép kiểm nghiệm Grubb (xem 7.3.4) cho trong bảng 5.
Đối với phép kiểm nghiệm Grubb cho một quan trắc bất thường, Các giá trị bất thường và phân tán tăng đến giá trị lớn hơn các giá trị tới hạn trong bảng 1% và 5%.
Đối với phép kiểm nghiệm Grubb cho hai quan trắc bất thường, Các giá trị bất thường và phân tán tăng đến giá trị nhỏ hơn các giá trị tới hạn trong bảng 1% và 5%.
8.3. Các chỉ số đối với số thống kê Mandel h và k (xem 7.3.1) cho trong bảng 6 và 7.
Bảng 5 – Các giá trị tới hạn đối với phép kiểm nghiệm Grubb
|
p |
Một quan trắc lớn nhất hoặc một quan trắc nhỏ nhất |
Hai quan trắc lớn nhất hoặc hai quan trắc nhỏ nhất |
||
|
Lớn hơn 1% |
Lớn hơn 5% |
Nhỏ hơn 1 % |
Nhỏ hơn 5% |
|
|
3 |
1.155 |
1.155 |
— |
— |
|
4 |
1.496 |
1.481 |
0.000 0 |
0.000 2 |
|
5 |
1.764 |
1.175 |
0.001 8 |
0.009 0 |
|
6 |
1.973 |
1.887 |
0.011 6 |
0.034 9 |
|
7 |
2.139 |
2.020 |
0.030 8 |
0.070 8 |
|
8 |
2.274 |
2.126 |
0.056 3 |
0.110 1 |
|
9 |
2.387 |
2.215 |
0.085 1 |
0.149 2 |
|
10 |
2.182 |
2.290 |
0,115 0 |
0.186 4 |
|
11 |
2.564 |
2.355 |
0.144 8 |
0.221 3 |
|
12 |
2.536 |
2.412 |
0.173 8 |
0.253 7 |
|
13 |
2.699 |
2.462 |
0.201 6 |
0.283 6 |
|
14 |
2.755 |
2.507 |
0.228 0 |
0.311 2 |
|
15 |
2.806 |
2.549 |
0.253 0 |
0.336 7 |
|
16 |
2.852 |
2.585 |
0.276 7 |
0.360 3 |
|
17 |
2.894 |
2.620 |
0.299 0 |
0.382 2 |
|
18 |
2.932 |
2.651 |
0.320 0 |
0.402 5 |
|
19 |
2.968 |
2.681 |
0.339 8 |
0.421 4 |
|
20 |
3.001 |
2.709 |
0.358 5 |
0.439 1 |
|
21 |
3.031 |
2.733 |
0.376 1 |
0.455 6 |
|
22 |
3.060 |
2.758 |
0.392 7 |
0.471 1 |
|
23 |
3.087 |
2.781 |
0.408 5 |
0.485 7 |
|
24 |
3.112 |
2.802 |
0.423 4 |
0.499 4 |
|
25 |
3.135 |
2.822 |
0.437 6 |
0.512 3 |
|
26 |
3.157 |
2.841 |
0.451 0 |
0.524 5 |
|
27 |
3.178 |
2.859 |
0.463 8 |
0.536 0 |
|
28 |
3.199 |
2.076 |
0.475 9 |
0.547 0 |
|
29 |
3.218 |
2.893 |
0.487 5 |
0.557 4 |
|
30 |
3.236 |
2.908 |
0.498 5 |
0.567 2 |
|
31 |
3.253 |
2.924 |
0.509 1 |
0.576 6 |
|
32 |
3.270 |
2.938 |
0.519 2 |
0.585 6 |
|
33 |
3.286 |
2.952 |
0.528 8 |
0.594 1 |
|
34 |
3.301 |
2.965 |
0.538 1 |
0.602 3 |
|
35 |
3.316 |
2.979 |
0.546 9 |
0.610 1 |
|
36 |
3.330 |
2.991 |
0.555 4 |
0.617 5 |
|
37 |
3.343 |
3.003 |
0.563 6 |
0.624 7 |
|
38 |
3.356 |
3.014 |
0.571 4 |
0.621 6 |
|
39 |
3.369 |
3.025 |
0.578 9 |
0.638 2 |
|
40 |
3.381 |
3.036 |
0.586 2 |
0.644 5 |
|
p = số phòng thí nghiệm ở mức đã cho |
||||
Bảng 6 – Các chỉ số đối với số thống kê Mandel h và k ở mức có nghĩa 1%
|
p |
h |
k |
||||||||
|
n |
||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
3 |
1,15 |
1,71 |
1,64 |
1,58 |
1,53 |
1,49 |
1,46 |
1,43 |
1,41 |
1,39 |
|
4 |
1,49 |
1,91 |
1,77 |
1,67 |
1,60 |
1,55 |
1,51 |
1,48 |
1,45 |
1,43 |
|
5 |
1,72 |
2,05 |
1,85 |
1,73 |
1,65 |
1,59 |
1,55 |
1,51 |
1,48 |
1,46 |
|
6 |
1,87 |
2,14 |
1,90 |
1,77 |
1,68 |
1,62 |
1,57 |
1,53 |
1,50 |
1,47 |
|
7 |
1,98 |
2,20 |
1,94 |
1,79 |
1,70 |
1,63 |
1,58 |
1,54 |
1,51 |
1,48 |
|
8 |
2,06 |
2,25 |
1,97 |
1,81 |
1,71 |
1,65 |
1,59 |
1,55 |
1,52 |
1,49 |
|
9 |
2,13 |
2,29 |
1,99 |
1,82 |
1,73 |
1,66 |
1,60 |
1,56 |
1,53 |
1,50 |
|
10 |
2,18 |
2,32 |
2,00 |
1,84 |
1,74 |
1,66 |
1,61 |
1,57 |
1,53 |
1,50 |
|
11 |
2,22 |
2,34 |
2,01 |
1,85 |
1,74 |
1,67 |
1,62 |
1,57 |
1,54 |
1,51 |
|
12 |
2,25 |
2,36 |
2,02 |
1,85 |
1,75 |
1,68 |
1,62 |
1,58 |
1,54 |
1,51 |
|
13 |
2,27 |
2,38 |
2,03 |
1,86 |
1,76 |
1,68 |
1,63 |
1,58 |
1,55 |
1,52 |
|
14 |
2,30 |
2,39 |
2,04 |
1,87 |
1,76 |
1,69 |
1,63 |
1,58 |
1,55 |
1,52 |
|
15 |
2,32 |
2,41 |
2,05 |
1,87 |
1,76 |
1,69 |
1,63 |
1,59 |
1,55 |
1,52 |
|
16 |
2,33 |
2,42 |
2,05 |
1,88 |
1,77 |
1,69 |
1,63 |
1,59 |
1,55 |
1,52 |
|
17 |
2,35 |
2,44 |
2,06 |
1,88 |
1,77 |
1,69 |
1,64 |
1,59 |
1,55 |
1,52 |
|
18 |
2,36 |
2,44 |
2,06 |
1,88 |
1,77 |
1,70 |
1,64 |
1,59 |
1,56 |
1,52 |
|
19 |
2,37 |
2,44 |
2,07 |
1,89 |
1,78 |
1,70 |
1,64 |
1,59 |
1,56 |
1,53 |
|
20 |
2,39 |
2,45 |
2,07 |
1,89 |
1,78 |
1,70 |
1,64 |
1,60 |
1,56 |
1,53 |
|
21 |
2,39 |
2,46 |
2,07 |
1,89 |
1,78 |
1,70 |
1,64 |
1,60 |
1,56 |
1,53 |
|
22 |
2,40 |
2,46 |
2,08 |
1,90 |
1,78 |
1,70 |
1,65 |
1,60 |
1,56 |
1,53 |
|
23 |
2,41 |
2,47 |
2,08 |
1,90 |
1,78 |
1,71 |
1,65 |
1,60 |
1,56 |
1,53 |
|
24 |
2,42 |
2,47 |
2,08 |
1,90 |
1,79 |
1,71 |
1,65 |
1,60 |
1,56 |
1,53 |
|
25 |
2,42 |
2,47 |
2,08 |
1,90 |
1,79 |
1,71 |
1,65 |
1,60 |
1,56 |
1,53 |
|
26 |
2,43 |
2,48 |
2,09 |
1,90 |
1,79 |
1,71 |
1,65 |
1,60 |
1,56 |
1,53 |
|
27 |
2,44 |
2,48 |
2,09 |
1,90 |
1,79 |
1,71 |
1,65 |
1,60 |
1,56 |
1,53 |
|
28 |
2,44 |
2,49 |
2,09 |
1,91 |
1,79 |
1,71 |
1,65 |
1,60 |
1,57 |
1,53 |
|
29 |
2,45 |
2,49 |
2,09 |
1,91 |
1,79 |
1,71 |
1,65 |
1,60 |
1,57 |
1,53 |
|
30 |
2,45 |
2,49 |
2,10 |
1,91 |
1,79 |
1,71 |
1,65 |
1,61 |
1,57 |
1,53 |
|
p = Số phòng thí nghiệm ở mức đã cho n = số lặp lại trong phạm vi mỗi phòng thí nghiệm ở một mức |
||||||||||
Bảng 7 – Các chỉ số đối với thống kê Mandel h và k ở mức có nghĩa 5%
|
p |
h |
k |
||||||||
|
n |
||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
3 |
1,15 |
1,65 |
1,53 |
1,45 |
1,40 |
1,37 |
1,34 |
1,32 |
1,30 |
1,29 |
|
4 |
1,42 |
1,76 |
1,59 |
1,50 |
1,44 |
1,40 |
1,37 |
1,35 |
1,33 |
1,31 |
|
5 |
1,57 |
1,81 |
1,62 |
1,53 |
1,46 |
1,42 |
1,39 |
1,36 |
1,34 |
1,32 |
|
6 |
1,66 |
1,85 |
1,64 |
1,54 |
1,48 |
1,43 |
1,40 |
1,37 |
1,35 |
1,33 |
|
7 |
1,71 |
1,87 |
1,66 |
1,55 |
1,49 |
1,44 |
1,41 |
1,38 |
1,36 |
1,34 |
|
8 |
1,75 |
1,88 |
1,67 |
1,56 |
1,50 |
1,45 |
1,41 |
1,38 |
1,36 |
1,34 |
|
9 |
1,78 |
1,90 |
1,68 |
1,57 |
1,50 |
1,45 |
1,42 |
1,39 |
1,36 |
1,35 |
|
10 |
1,80 |
1,90 |
1,68 |
1,57 |
1,50 |
1,46 |
1,42 |
1,39 |
1,37 |
1,35 |
|
11 |
1,82 |
1,91 |
1,69 |
1,58 |
1,51 |
1,46 |
1,42 |
1,39 |
1,37 |
1,35 |
|
12 |
1,83 |
1,92 |
1,69 |
1,58 |
1,51 |
1,46 |
1,42 |
1,40 |
1,37 |
1,35 |
|
13 |
1,84 |
1,92 |
1,69 |
1,58 |
1,51 |
1,46 |
1,43 |
1,40 |
1,37 |
1,35 |
|
14 |
1,85 |
1,92 |
1,70 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,37 |
1,35 |
|
15 |
1,86 |
1,93 |
1,70 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
16 |
1,86 |
1,93 |
1,70 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
17 |
1,87 |
1,93 |
1,70 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
18 |
1,88 |
1,93 |
1,71 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
19 |
1,88 |
1,93 |
1,71 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
20 |
1,89 |
1,94 |
1,71 |
1,59 |
1,52 |
1,47 |
1,43 |
1,40 |
1,38 |
1,36 |
|
21 |
1,89 |
1,94 |
1,71 |
1,60 |
1,52 |
1,47 |
1,44 |
1,41 |
1,38 |
1,36 |
|
22 |
1,89 |
1,94 |
1,71 |
1,60 |
1,52 |
1,47 |
1,44 |
1,41 |
1,38 |
1,36 |
|
23 |
1,90 |
1,94 |
1,71 |
1,60 |
1,53 |
1,47 |
1,44 |
1,41 |
1,38 |
1,36 |
|
24 |
1,90 |
1,94 |
1,71 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,38 |
|
25 |
1,90 |
1,94 |
1,71 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
26 |
1,90 |
1,34 |
1,71 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
27 |
1,91 |
1,94 |
1,71 |
1,60 |
1,53 |
1,48 |
1 44 |
1,41 |
1,38 |
1,36 |
|
28 |
1,91 |
1,94 |
1,71 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
29 |
1,91 |
1,94 |
1,72 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
30 |
1,91 |
1,94 |
1,72 |
1,60 |
1,53 |
1,48 |
1,44 |
1,41 |
1,38 |
1,36 |
|
p = số phòng thí nghiệm ở mức đã cho n = số lặp lại trong phạm vi mỗi phòng thí nghiệm ở một mức |
||||||||||
PHỤ LỤC A
(quy định)
Các ký hiệu và chữ viết tắt dùng trong TCVN 6910
a Phần bị chắn trong mối quan hệ
s – a + bm
A Yếu tố dùng để tinh độ knỏng đảm bảo của ước lượng
b Độ dốc trong mối quan hệ
s = a + bm
B Thành phần trong kết quả thử nghiệm biểu thị độ lệch của phòng thí nghiệm so với trung bình chung (thành phần phòng thí nghiệm của độ chệch)
B0 Thành phần của B biểu thị tất cả các yếu tố không thay đổi trong điều kiện chụm trung gian
B(1), B(2) Các thành phần của B biểu thị những yếu tố thay đổi trong điều kiện chụm trung gian
c Phần bị chắn trong mối quan hệ
Ig s = c + d Ig m
C. C’. C” Các thống kê kiểm nghiệm
Ccrit. C’crit . C”crit Các giá trị tới hạn đối với những phép kiểm nghiệm thống kê
CDp Độ sai khác tới hạn với xác suất p
CRp Phạm vi tới hạn với xác suất p
d Độ dốc trong mối liên hệ
Ig s = c + d Ig m
e Thành phần trong kết quả thử nghiệm biểu thị sai số ngẫu nhiên tồn tại trong mọi kết quả thử nghiệm
f Yếu tố phạm vi tới hạn
Fp(v1. v2) Phân vị mức p của phân bố F với các bậc tự do v1 và v2
G Thống kê kiểm nghiệm Grubb
h Thống kê kiểm nghiệm nhất quán giữa các phòng thí nghiệm của Mandel
k Thống kê kiểm nghiệm nhất quán trong phóng thí nghiệm của Mandel
LCL Giới hạn kiểm soát dưới (hoặc giới hạn hành động hoặc giới hạn cảnh báo)
m Trung bình chung của đặc tính thử; mức
M Yếu tố được xem xét trong điều kiện chụm trung gian
N Số phép lặp
n Số kết quả thử nghiệm thu được của phòng thí nghiệm tại một mức
p Số phòng thí nghiệm tham gia thí nghiệm liên phòng
P Xác suất
q Số lượng các mức của đặc tính thử nghiệm trong thí nghiệm liên phòng
r Giới hạn lặp lại
R Giới hạn tái lập
RM Mẫu chuẩn
s Ước lượng của độ lệch chuẩn
![]() Độ lệch chuẩn đự đoán
Độ lệch chuẩn đự đoán
T Tổng thể hoặc tổng của biểu thức nào đó
t Số các đối tượng thử nghiệm hoặc số nhóm
UCL Giới hạn kiểm soát trên (hoặc giới hạn hành động hoặc giới hạn cảnh báo)
W Yếu tố trọng số sử dụng trong tính toán hồi quy trọng số
w Độ rộng của tập hợp các kết quả thử nghiệm
x Dữ liệu sử dụng cho thử nghiệm Grubb
y Kết quả thử nghiệm
![]() Trung bình số học của kết quả thử nghiệm
Trung bình số học của kết quả thử nghiệm
![]() Trung bình chung của kết quả thử nghiệm
Trung bình chung của kết quả thử nghiệm
α Mức ý nghĩa
β Xác suất sai lầm loại II
g Tỷ số giữa độ lệch chuẩn tái lập và độ lệch chuẩn lặp lại (sR/sr)
D Độ chệch phòng thí nghiệm
![]() Ước lượng của D
Ước lượng của D
d Độ chệch của phương pháp đo
![]() Ước lượng của d
Ước lượng của d
l Sự sai khác phát hiện được giữa các độ chệch của hai phòng thí nghiệm hoặc các độ chệch của hai phương pháp đo
m Giá trị thực hoặc giá trị quy chiếu được chấp nhận của đặc tính thử nghiệm
v Số bậc tự do
p Tỷ số phát hiện được giữa độ lệch chuẩn lặp lại của phương pháp B và phương pháp A
s Giá trị thực của độ lệch chuẩn
t Thành phần của kết quả thử nghiệm biểu thị sự thay đổi theo thời gian từ lần hiệu chuẩn cuối cùng
f Tỷ số phát hiện được giữa căn bậc hai của bình phương trung bình giữa các phòng thí nghiệm của phương pháp B và phương pháp A
X2p(v) Phân vị mức p của phân bố X2 với bậc tự do v
Các ký hiệu được sử dụng như chỉ số
C Sự khác nhau về hiệu chuẩn
E Sự khác nhau về thiết bị
i Chỉ số của một phòng thí nghiệm cụ thể
I( ) Chỉ số của thước đo trung gian của độ chụm, trong dấu ngoặc chỉ loại tình huống trung gian
j Chỉ số của một mức cụ thể (TCVN 6910-2)
Chỉ số của một nhóm phép thử nghiệm hoặc một yếu tố (TCVN 6910-3)
k Chỉ số của một kết quả thử nghiệm cụ thể trong phòng thí nghiệm i ở mức j
L Liên phòng thí nghiệm (liên phòng)
m Chỉ số của độ chệch có thể biết được
M Mẫu thử liên phòng
O Sự khác nhau về người thao tác
P Xác suất
r Độ lặp lại
R Độ tái lập
T Sự khác nhau về thời gian
W Phòng thí nghiệm thành viên
1, 2, 3 … Đối với các kết quả thử nghiệm, đánh số theo thứ tự thu nhận chúng
(1), (2), (3) … Đối với các kết quả thử nghiệm, đánh số theo thứ tự tăng độ lớn
PHỤ LỤC B
(tham khảo)
Các ví dụ phân tích thống kê thí nghiệm độ chụm
B.1 Ví dụ 1: Xác định hàm lượng lưu huỳnh trong than đá (với một số mức không có số liệu thiếu hoặc bất thường)
B.1.1 Cơ sở
a) Phương pháp đo
Xác định hàm lượng lưu huỳnh trong than đá với kết quả thử nghiệm thể hiện theo phần trăm khối lượng.
b) Nguồn
Tomkin, S.S. Hoá học kỹ thuật và công nghiệp, (xem tài liệu tham khảo [6] trong phụ lục C.)
c) Mô tả
Tám phòng thí nghiệm tham gia tiến hành phân tích theo phương pháp đo đã được tiêu chuẩn hoá mô tả trong nguồn tài liệu đã nêu. Phòng thí nghiệm 1 báo cáo bốn kết quả thử nghiệm và phòng thí nghiệm 5 báo cáo bốn hoặc năm; Các phòng thí nghiệm còn lại tiến hành ba phép đo.
d) Biểu diễn đồ thị
Số thống kê Mandel h và k cần được vẽ thành đồ thị, nhưng vì trong ví dụ này chúng không quan trọng lắm nên được bỏ đi để dành chỗ cho việc trình bày các số liệu bằng đồ thị trong một ví dụ khác. Các đồ thị số Mandel được minh hoạ đầy đủ và thảo luận trong ví dụ ở B.3.
B.1.2 Số liệu gốc
Số liệu gốc được trình bày bằng % khối lượng [%(m/m)], trong bảng B.1 theo biểu mẫu A trong hình 2 (xem 7.2.8) và không có chú thích riêng nào.
Những số liệu đó được trình bày bằng đồ thị trong các hình từ B.1 đến B.4.
Bảng B.1 – Số liệu gốc: Hàm lượng lưu huỳnh trong than dá
|
Phòng thí nghiệm i |
|
Mức j |
|
|
|
1 |
2 |
3 |
4 |
|
|
|
0,71 |
1,20 |
1,68 |
3,26 |
|
1 |
0,71 |
1,18 |
1,70 |
3,26 |
|
|
0,70 |
1,23 |
1,68 |
3,20 |
|
|
0,71 |
1,21 |
1,69 |
3,24 |
|
|
0,69 |
1,22 |
1,64 |
3,20 |
|
2 |
0,67 |
1,21 |
1,64 |
3,20 |
|
|
0,68 |
1,22 |
1,65 |
3,20 |
|
|
0,66 |
1,28 |
1,61 |
3,37 |
|
3 |
0,65 |
1,31 |
1,61 |
3,36 |
|
|
0,69 |
1,30 |
1 62 |
3,38 |
|
|
0,67 |
1,23 |
1,68 |
3,16 |
|
4 |
0,65 |
1,18 |
1,66 |
3,22 |
|
|
0,66 |
1,20 |
1,66 |
3,23 |
|
|
0,70 |
1,31 |
1,64 |
3,20 |
|
|
0,69 |
1,22 |
1,67 |
3,19 |
|
5 |
0,66 |
1,22 |
1,60 |
3,18 |
|
|
0,71 |
1,24 |
1,66 |
3,27 |
|
|
0,69 |
— |
1,68 |
3,24 |
|
|
0,73 |
1,39 |
1,70 |
3,27 |
|
6 |
0,74 |
1,36 |
1,73 |
3,31 |
|
|
0,73 |
1,37 |
1,73 |
3,29 |
|
|
0,71 |
1,20 |
1,69 |
3,27 |
|
7 |
0,71 |
1,26 |
1,70 |
3,24 |
|
|
0,69 |
1,26 |
1,68 |
3,23 |
|
|
0,70 |
1,24 |
1,67 |
3,25 |
|
8 |
0,65 |
1,22 |
1,68 |
3,26 |
|
|
0,68 |
1,30 |
1,67 |
3,26 |
Chú thích 8 – Với thí nghiệm nêu trong bảng B.1, các phòng thí nghiệm không được hướng dẫn thực hiện bao nhiêu phép đo mà chỉ đưa ra số lượng phép đo tối thiểu. Theo quy trình đã khuyến nghị trong tiêu chuẩn này, cần phải thực hiện một sự lựa chọn ngẫu nhiên các giá trị đã cho ở phòng thí nghiệm 1 và 5 để giảm xuống chính xác còn ba kết quả thử nghiệm ở tất cả các ô. Tuy nhiên, để minh hoạ quy trình tính toán cho các số lượng khác nhau của kết quả thử nghiệm, tất cả kết quả thử nghiệm được giữ lại trong ví dụ này. Có thể tiến hành lựa chọn ngẫu nhiên để giảm số kết quả thử nghiệm xuống còn 3 trong mỗi ô nếu muốn xác minh rằng một quy trình như vậy ít có ảnh hưởng đến các giá trị ![]() , sr và sR.
, sr và sR.
B.1.3. Tính trung bình ô (![]() )
)
Trung bình ô được cho theo % khối lượng [%(m/m)]. trong bàng B.2 với biểu mẫu B của hình 2 (xem 7.2.9).
B.1.4 Tính độ lệch chuẩn (sij)
Độ lệch chuẩn được cho theo % khối lượng [%(m/m)], trong bảng B.3 với biểu mẫu C ở hình 2 (xem 7.2.10).
B.1.5 Xem xét sự nhất quán và các giá trị bất thường
Phép kiểm nghiệm Cochran với n = 3 và p = 8 phòng thí nghiệm cho các giá trị tới hạn 0,516 đối với 5% và 0,615 đối với 1%.
Với mức 1, giá trị lớn nhất của s trong phòng thí nghiệm 8:
Ss2 = 0,001 82; giá trị thử nghiệm = 0,347
với mức 2, giá trị lớn nhất của s trong phòng thí nghiệm 5
Ss2 = 0,006 36; giá trị thử nghiệm = 0,287
Với mức 3, giá trị lớn nhất của s trong phòng thí nghiệm 5:
Ss2 = 0,001 72: giá trị thử nghiệm = 0,598
với mức 4, giá trị lớn nhất trong phòng thí nghiệm 4
Ss2 = 0,004 63: giá trị thử nghiệm = 0,310
Bảng B.2 – Trung bình ô: hàm lượng lưu huỳnh của than đá
|
Phòng thí nghiệm i |
Mức j |
|||||||
|
1 |
2 |
3 |
4 |
|||||
|
|
nij |
|
nij |
|
nij |
|
nij |
|
|
1 |
0,708 |
4 |
1,205 |
4 |
1,588 |
4 |
3,240 |
4 |
|
2 |
0,680 |
3 |
1,217 |
3 |
1,643 |
3 |
3,200 |
3 |
|
3 |
0,667 |
3 |
1,297 |
3 |
1,613 |
3 |
3,370 |
3 |
|
4 |
0,660 |
3 |
1,203 |
3 |
1,667 |
3 |
3,203 |
3 |
|
5 |
0,690 |
5 |
1,248 |
4 |
1,650 |
5 |
3,216 |
5 |
|
6 |
0,733 |
3 |
1,373 |
3 |
1,720 |
3 |
3,290 |
3 |
|
7 |
0,703 |
3 |
1,240 |
3 |
1,690 |
3 |
3,247 |
3 |
|
8 |
0,677 |
3 |
1,253 |
3 |
1,673 |
3 |
3,257 |
3 |
Bảng B.3 – Độ lệch chuẩn: hàm lượng lưu huỳnh trong than đá
|
Phòng Thí nghiệm i |
Mức j |
|||||||
|
1 |
2 |
3 |
4 |
|||||
|
sij |
nij |
sij |
nij |
sij |
nij |
sij |
nij |
|
|
1 |
0,005 |
4 |
0,021 |
4 |
0,010 |
4 |
0,028 |
4 |
|
2 |
0,010 |
3 |
0,006 |
3 |
0,006 |
3 |
0,000 |
3 |
|
3 |
0,021 |
3 |
0,015 |
3 |
0,006 |
3 |
0,010 |
3 |
|
4 |
0,010 |
3 |
0,025 |
3 |
0,012 |
3 |
0,038 |
3 |
|
5 |
0,019 |
5 |
0,043 |
4 |
0,032 |
5 |
0,038 |
5 |
|
6 |
0,006 |
3 |
0,015 |
3 |
0,017 |
3 |
0,020 |
3 |
|
7 |
0,012 |
3 |
0,035 |
3 |
0,010 |
3 |
0,021 |
3 |
|
8 |
0,025 |
3 |
0,042 |
3 |
0,006 |
3 |
0,006 |
3 |
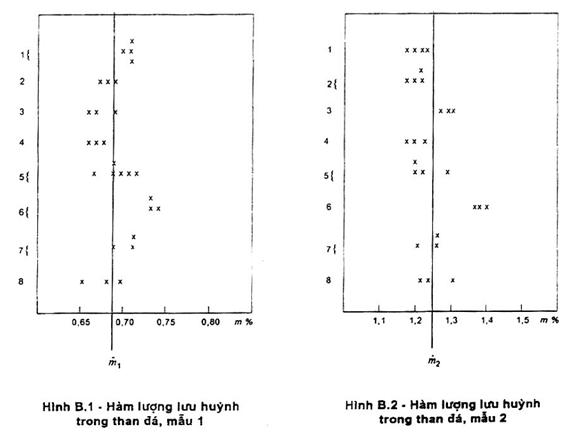
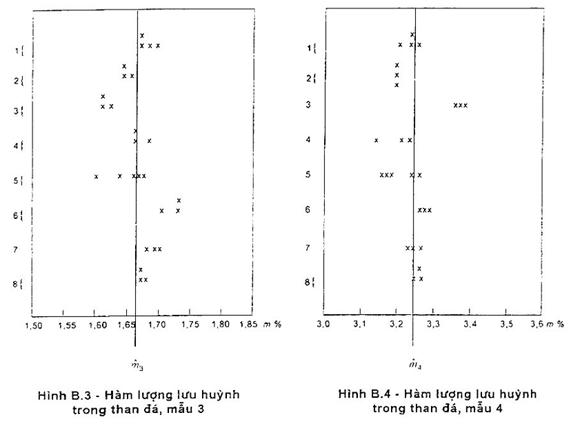
Điều đó chỉ ra rằng một ô ở mức 3 có thể được coi như giá trị tản mạn, và ở đó không có giá trị bất thường, giá trị tản mạn đó được giữ lại trong tính toán tiếp theo.
Các phép kiểm nghiệm Grubb đã được áp dụng cho các trung bình ô, đưa ra các giá trị trong bảng B.4. Ở đó không có giá trị tản mạn hoặc giá trị bất thường đơn. Ở mức 2 và 4, các kết quả cao đối với phòng thí nghiệm 3 và 6 là giá trị tản mạn theo phép thử kép cao; chúng được giữ lại trong phân tích.
Bảng B.4 – Ứng dụng phép kiểm nghiệm Grubb cho trung bình ô
|
Mức |
Đơn thấp |
Đơn cao |
Kép thấp |
Kép cao |
Kiểu phép Ihử |
|
1 |
1,24 |
1,80 |
0,539 |
0,298 |
Phép kiểm nghiệm thống kê Grubb |
|
2 |
0,91 |
2,09 |
0,699 |
0,108 |
|
|
3 |
1,67 |
1,58 |
0,378 |
0,459 |
|
|
4 |
0,94 |
2,09 |
0,679 |
0,132 |
|
|
Giá trị tản mạn |
2,126 |
2,126 |
0,110 1 |
0,110 1 |
Giá trị tới hạn Grubb |
|
Giá trị bất thường |
2,274 |
2,274 |
0,056 3 |
0,056 3 |
B.1.6 Tính toán ![]() , srj và sRj
, srj và sRj
Các phương sai định nghĩa ở 7.4.4 và 7.4.5 được tính toán bằng cách sử dụng mức 1 làm ví dụ
như sau:
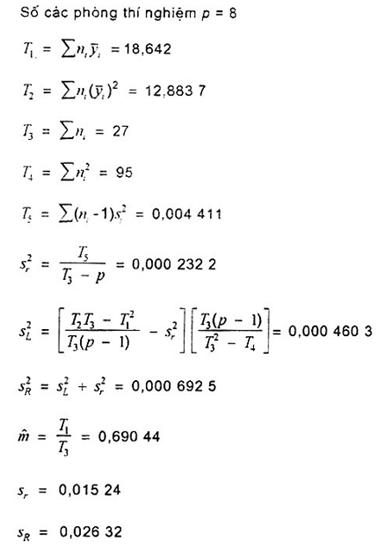
Việc tính toán cho các mức 2,3 và 4 có thể được tiến hành tương tự để đưa ra các kết quả trong bảng B.5
Bảng B.5 – Các giá trị tính toán của ![]() , srj và sRj cho hàm lượng lưu huỳnh của than dá
, srj và sRj cho hàm lượng lưu huỳnh của than dá
|
Mức j |
pj |
|
srj |
sRj |
|
1 |
8 |
0,690 |
0,015 |
0,026 |
|
2 |
8 |
1,252 |
0,029 |
0,061 |
|
3 |
8 |
1,667 |
0,017 |
0,035 |
|
4 |
8 |
3,250 |
0,026 |
0,058 |
B.1.7 Sự phụ thuộc của độ chụm vào m
Sự kiểm tra các số liệu trong bàng B5 không chỉ ra bất cứ sự phụ thuộc nào và các giá trị trung bình có thể được sử dụng.
B.1.8 Kết luận
Độ chụm của phương pháp đo phải tính theo % khối lượng
Độ lệch chuẩn lặp lại, sr = 0,022
Độ lệch chuẩn tái lập, sR = 0,045
Các giá trị đó có thể được áp dụng trong phạm vi từ 0,69% (m/m) đến 3,25 % (m/m). Chúng được xác định từ các thí nghiệm đồng mức gồm 8 phòng thí nghiệm phủ phạm vi đó của các giá trị, trong đó có bốn giá trị tản mạn được phát hiện và giữ lại.
B.2 – Ví dụ 2: Điểm hoá mềm của nhựa (với một số mức có số liệu thiếu)
B.2.1 Cơ sở
a) Phương pháp đo
Xác định điểm hoá mềm của nhựa bằng vòng và bình cầu.
b) Nguồn
Các phương pháp tiêu chuẩn để thử nghiệm nhựa đường và các sản phẩm của nó; Lĩnh vực về nhựa; Dãy phương pháp No. PT3 sử dụng glycerin trung tính (tài liệu tham khảo [5] trong phụ lục C).
c) Vật liệu
Được lựa chọn từ các lô nhựa thương phẩm và được chuẩn bị theo chương “mẫu thử” của lĩnh vực nhựa trong tài liệu tham khảo [5]
d) Mô tả
Đây là việc xác định một tính chất, bao gồm việc đo nhiệt độ theo độ Celsius. 16 phòng thí nghiệm cùng hợp tác. Tiến hành đo 4 mẫu ở khoảng 87,5 0C; 92,50C; 97,50C và 102 0C để phủ được phạm vi sản phẩm thương mại thông thường, nhưng vật liệu được chọn nhằm để bao trùm ở mức 2 với nhiệt độ trung bình khoảng 960C tương tự như ở mức 3. Phòng thí nghiệm 5 lúc đầu áp dụng không đúng phương pháp cho mẫu thử ở mức 2 ( mẫu đầu tiên đã đo) sau đó vật liệu còn lại chỉ đủ cho một phép đo. Phòng thí nghiệm 8 không còn mẫu thử cho mức 1 (có 2 mẫu ở mức 4).
e) Biểu diễn bằng đồ thị
Các số thống kê Mandel h và k phải được vẽ thành đồ thị nhưng trong ví dụ này chúng được bỏ qua để đưa ra một dạng trình bày các số liệu bằng sơ đồ khác. Các đồ thị Mandel được minh họa và thảo luận đầy đủ trong ví dụ đưa ra ở B.3.
B.2.2 Số liệu gốc
Số liệu gốc được trình bày trong bảng B.6, theo độ Celsius, ở biểu mẫu A trong hình 2 (xem 7.2.8)
Bảng B.6 – số liệu gốc: điểm hoá mềm của nhựa (°C)
|
Phòng thí nghiệm i |
Mức j |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
91,0 |
97,0 |
96,5 |
104,0 |
|
|
89,6 |
97,2 |
97,0 |
104,0 |
|
2 |
89,7 |
98,5 |
97,2 |
102,6 |
|
|
89,8 |
97,2 |
97,0 |
103,6 |
|
3 |
88,0 |
97,8 |
94,2 |
103,0 |
|
|
87,5 |
94,5 |
95,8 |
99,5 |
|
4 |
89,2 |
96,8 |
96,0 |
102,5 |
|
|
88,5 |
97,5 |
98,0 |
103,5 |
|
5 |
89,0 |
97,2 |
98,2 |
101,0 |
|
|
90,0 |
— |
98,5 |
100,2 |
|
6 |
88,5 |
97,8 |
99,5 |
102,2 |
|
|
90,5 |
97,2 |
103,2 |
102,0 |
|
7 |
88,9 |
96,6 |
98,2 |
102,8 |
|
|
88,2 |
97,5 |
99,0 |
102,2 |
|
8 |
— |
96,0 |
98,4 |
102,6 |
|
|
— |
97,5 |
97,4 |
103,9 |
|
9 |
90,1 |
95,5 |
98,2 |
102,8 |
|
|
88,4 |
96,8 |
96,7 |
102,0 |
|
10 |
86,0 |
95,2 |
94,8 |
99,8 |
|
|
85,8 |
95,0 |
93,0 |
100,8 |
|
11 |
87,6 |
93,2 |
93,6 |
98,2 |
|
|
84,4 |
93,4 |
93,9 |
97,8 |
|
12 |
88,2 |
95,8 |
95,8 |
101,7 |
|
|
87,4 |
95,4 |
95,4 |
101,2 |
|
13 |
91,0 |
98,2 |
98,0 |
104,5 |
|
|
90,4 |
99,5 |
97,0 |
105,6 |
|
14 |
87,5 |
97,0 |
97,1 |
105,2 |
|
|
87,8 |
95,5 |
96,6 |
101,8 |
|
15 |
87,5 |
95,0 |
97,8 |
101,5 |
|
|
87,6 |
95,2 |
99,2 |
100,9 |
|
16 |
88,8 |
95,0 |
97,2 |
99,5 |
|
|
85,0 |
93,2 |
97,8 |
99,8 |
|
Chú thích – Không có các giá trị tản mạn hoặc giá trị bất thường thống kê rõ ràng |
||||
B.2.3 Trung bình của ô
Trung bình của ô được trình bày trong bảng B.7 theo độ Celsius, trong biểu mẫu B ở hình 2 (xem 7.2.9)
Những số liệu này được trình bày bằng đồ thị ở hình B.5
B.2.4 Độ lệch tuyệt đối trong các ô
Trong ví dụ này có 2 kết quả thử nghệm cho từng ô và độ lệch tuyệt đối có thể được dùng để thể hiện khả năng thay đổi. Độ lệch tuyệt đối trong các ô theo độ Celsius, được đưa ra ở bảng B.8 theo biểu mẫu C trong hình 2 (xem 7.2.10)
Những số liệu này được trình bày bằng đồ thị ở hình B.6
Bảng B.7 – Trung bình của ô: điểm hoá mềm của nhựa (°C)
|
Phòng thí nghiệm i |
Mức j |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
90,30 |
97,10 |
96,75 |
104,00 |
|
2 |
89,75 |
97,85 |
97,10 |
103,10 |
|
3 |
87,75 |
96,15 |
95,00 |
101,25 |
|
4 |
88,85 |
97,15 |
97,00 |
103,00 |
|
5 |
89,50 |
— |
98,35 |
100,60 |
|
6 |
89,50 |
97,50 |
101,35 |
102,10 |
|
7 |
88,55 |
97,05 |
98,60 |
102,50 |
|
8 |
— |
96,75 |
97,90 |
103,25 |
|
9 |
89,25 |
96,15 |
97,45 |
102,40 |
|
10 |
85,90 |
95,10 |
93,90 |
100,30 |
|
11 |
86,00 |
93,30 |
93,75 |
98,00 |
|
12 |
87,80 |
95,60 |
95,60 |
101,45 |
|
13 |
90,70 |
98,85 |
97,50 |
105,05 |
|
14 |
87,65 |
96,25 |
96,85 |
103,50 |
|
15 |
87,55 |
95,10 |
98,50 |
101,20 |
|
16 |
86,90 |
94,10 |
97,50 |
99,65 |
|
Chú thích – Giá trị đối với i = 5, j = 2 bị loại bỏ (xem 7.4.3) 1 |
||||
Bảng B.8 – Độ lệch tuyệt đối trong phạm vi ô: diểm hoá mềm của nhựa (°C)
|
Phòng thí nghiệm i |
Mức j |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
1,4 |
0,2 |
0,5 |
0,0 |
|
2 |
0,1 |
1,3 |
0,2 |
1,0 |
|
3 |
0,5 |
3,3 |
1,6 |
3,5 |
|
4 |
0,7 |
0,7 |
2,0 |
1,0 |
|
5 |
1,0 |
— |
0,3 |
0,8 |
|
6 |
2,0 |
0,6 |
3,7 |
0,2 |
|
7 |
0,7 |
0,9 |
0,8 |
0,6 |
|
8 |
– |
1,5 |
1,0 |
1,3 |
|
9 |
1,7 |
1,3 |
1,5 |
0,8 |
|
10 |
0,2 |
0,2 |
1,8 |
1,0 |
|
11 |
3,2 |
0,2 |
0,3 |
0,4 |
|
12 |
0,8 |
0,4 |
0,4 |
0,5 |
|
13 |
0,6 |
1,3 |
1,0 |
1,1 |
|
14 |
0,3 |
1,5 |
0,5 |
3,4 |
|
15 |
0,1 |
0,2 |
1,4 |
0,6 |
|
16 |
3,8 |
1,8 |
0,6 |
0,3 |
B.2.5 Xem xét sự nhất quán và các giá trị bất thường
Ứng dụng phép kiểm nghiệm Cochran dẫn đến các giá trị của số thống kê kiểm nghiệm C đưa ra trong bảng B.9
Các giá trị tới hạn ( xem 8.1) ở mức 5% là 0,471 cho p = 15 và 0,452 cho p = 16, trong đó n = 2. Không một giá trị tản mạn nào được chỉ ra.
Các phép kiểm nghiệm Grubb được áp dụng cho trung bình của ô. Không một giá trị tản mạn đơn hoặc kép hoặc giá trị bất thường nào được tìm thấy.
B.2.6 Tính ![]() , srj và sRj
, srj và sRj
Tính theo 7.4.4 và 7.4.5
Ví dụ, sử dụng mức 1, tính như dưới đây. Để lấy trung bình dễ dàng, tất cả các số liệu đều được trừ đi 80,000. Sử dụng phương pháp với n = 2 phép lặp lại đối với từng ô .
Số phòng thí nghiệm p = 15
Số phép lặp lại n = 2
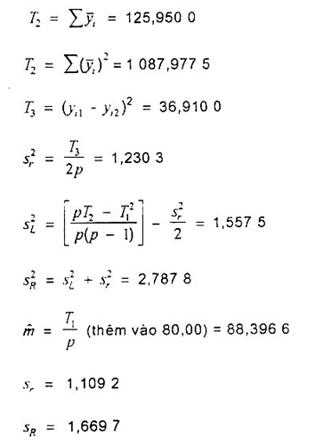
Các giá trị ở tất cả bốn mức được trình bày trong bảng B.11
Bảng B.9 – Các giá trị của số thống kê thử nghiệm Cochran, c
|
Mức j |
1 |
2 |
3 |
4 |
|
C |
0,391 (15) |
0,424 (15) |
0,434 (16) |
0,380 (16) |
|
Chú thích – Số phòng thí nghiệm được cho trong ngoặc đơn |
|
|||
Bảng B.10 – Áp dụng phép kiểm nghiệm Grubb cho trung bình ô
|
Mức; n |
Đơn thấp |
Đơn cao |
Kép thấp |
Kép cao |
Kiểu phép thử |
|
1; 15 |
1,69 |
1,56 |
0,546 |
0,662 |
Phép kiểm nghiệm thống kê Grubb |
|
2; 15 |
2,04 |
1,77 |
0,478 |
0,646 |
|
|
3; 16 |
1,76 |
2,27 |
0,548 |
0,566 |
|
|
4; 16 |
2,22 |
1,74 |
0.500 |
0,672 |
|
|
Giá trị tản mạn |
|
|
|
|
Giá trị tới hạn Grubb |
|
n =15 |
2,549 |
2,549 |
0,336 7 |
0,336 7 |
|
|
n = 16 |
2.585 |
2.585 |
0,360 3 |
0,360 3 |
|
|
Giá trị bất thường |
|
|
|
|
|
|
n =15 |
2.806 |
2.806 |
0,253 0 |
0,253 0 |
|
|
n = 16 |
2.852 |
2.852 |
0.276 7 |
0.276 7 |
|
Bảng B.11 – Các giá trị tính được của ![]() , srj và sRj đối với điểm hoá mềm của nhựa
, srj và sRj đối với điểm hoá mềm của nhựa
|
Mức j |
pj |
|
srj |
sRj |
|
1 |
15 |
88,40 |
1,109 |
1,670 |
|
2 |
15 |
96,27 |
0,925 |
1,597 |
|
3 |
16 |
97,07 |
0,993 |
2,010 |
|
4 |
16 |
101,96 |
1,004 |
1,915 |
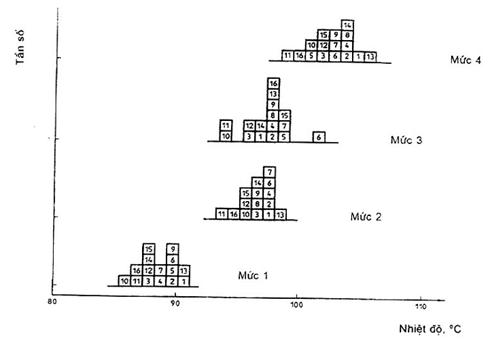
Hình B.5 – Điểm hoá mềm của nhựa: giá trị trung bình
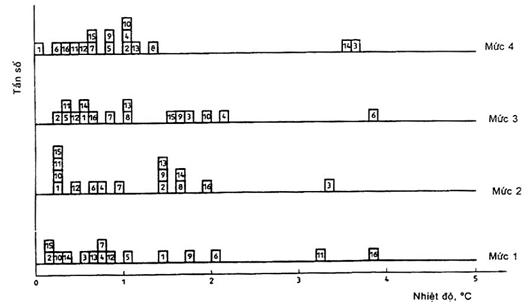
Hình B.6 – Điểm hoá mém của nhựa: độ lệch tuyệt đối trong phạm vi ô
B.2.7 Sự phụ thuộc của độ chụm vào giá trị m.
Kiểm tra nhanh bảng B.11 khỏng thấy sự phụ thuộc rõ ràng, trừ trường hợp độ tái lập. Sự thay đổi trong phạm vi giá trị m, nếu có thì là quá nhỏ có thể bỏ qua. Hơn nữa, xem xét trong phạm vi nhỏ các giá trị của m và bản chất của phép đo, thì sự phụ thuộc vào m khó có thể xảy ra. Như vậy, có thể yên tâm kết luận rằng độ chụm không phụ thuộc vào m trong phạm vi được công bố là bao trùm vật liệu thương mại thông thường. Như vậy các giá trị trung bình có thể được coi là giá trị cuối cùng cho độ lệch chuẩn lặp lại và tái lập.
B.2.8 Kết luận
Trong thực tế, các giá trị độ chụm của phương pháp có thể xem là độc lập với mức của vật liệu và bằng:
Độ lệch chuẩn lặp lại: sr = 1,0 °C
Độ lệch chuẩn tái lập: sR= 1,8 °C
B.3 Ví dụ 3: Chuẩn độ dầu Creosote bằng phương pháp nhiệt, (với một số mức có số liệu bất thường)
B.3.1 Cơ sở
a) Nguồn:
Các phương pháp tiêu chuẩn để thử nghiệm nhựa đường và các sản phẩm của nó- dầu Creosote; Phương pháp số hiệu Co. 18 (tài liệu tham khảo [5] trong phụ lục C).
b) Vật liệu:
Được chọn từ các lô thương phẩm của dầu Creosote được tập hợp và chuẩn bị theo quy định trong chương “Mẫu thử” thuộc lĩnh vực dầu creosote của tài liệu tham khảo [5].
c) Mô tả:
Là phương pháp đo tiêu chuẩn cho các phép phân tích hoá, bao hàm việc chuẩn độ bằng phương pháp nhiệt, với những kết quả diễn tả theo phần trăm khối lượng. 9 phòng thí nghiệm tham gia đo lặp lại 5 mẫu. Các mẫu đo được chọn sao cho bao trùm được phạm vi các loại dầu thường dùng trong thương mại. Chúng được chọn ở các mức xấp xỉ 4, 8, 12, 16, 20 (% (m/m)]. Thông thường những kết quả được ghi lại chỉ lấy đến 1 chữ số thập phân, nhưng đối với thí nghiệm này thì các thao tác viên được hướng dẫn lấy đến 2 số thập phân.
B.3.2 Số liệu gốc
Số liệu gốc được trình bày trong bàng 6.12. theo % khối lượng, với biểu mẫu A của hình 2 (xem 7.2.8). Kết quả thử nghiệm ở phòng thí nghiệm 1 luôn luôn cao hơn và ở một số mức cao hơn rõ rệt so với kết quả của các phòng khác.
Kết quả thử nghiệm thứ 2 ở phòng thí nghiệm 6 tại mức 5 còn chưa chính xác, giá trị được ghi lại có thể sẽ phù hợp hơn ở mức 4.
Những vấn đề này sẽ được tiếp tục thảo luận thêm ở phần B.3.5.
Bảng B.12 – số liệu gốc: Chuẩn độ dầu creosote bằng phương pháp nhiệt
|
Phòng thí nghiệm i |
Mức j |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
||||||
|
1 |
4,44 |
4,39 |
9,34 |
9,34 |
17,40 |
16,90 |
19,23 |
19,23 |
24,28 |
24,00 |
|
2 |
4,03 |
4,23 |
8,42 |
8,33 |
14,42 |
14,50 |
16,06 |
16,22 |
20,40 |
19,91 |
|
3 |
3,70 |
3,70 |
7,60 |
7,40 |
13,60 |
13,60 |
14,50 |
15,10 |
19,30 |
19,70 |
|
4 |
4,10 |
4,10 |
8,93 |
8,80 |
14,60 |
14,20 |
15,60 |
15,50 |
20,30 |
20,30 |
|
5 |
3,97 |
4,04 |
7,89 |
8,12 |
13,73 |
13,92 |
15,54 |
15,78 |
20,53 |
20,88 |
|
6 |
3,75 |
4,03 |
8,76 |
9,24 |
13,90 |
14,06 |
16,42 |
16,58 |
18,56 |
16,58 |
|
7 |
3,70 |
3,80 |
8,00 |
8,30 |
14,10 |
14,20 |
14,90 |
16,00 |
19,70 |
20,50 |
|
8 |
3,91 |
3,90 |
8,04 |
8,07 |
14,84 |
14,84 |
15,41 |
15,22 |
21,10 |
20,78 |
|
9 |
4,02 |
4,07 |
8,44 |
8,17 |
14,24 |
14,10 |
15,14 |
15,44 |
20,71 |
21,66 |
Bảng B.13 – Trung bình của ô: Chuẩn độ dầu creosote bằng phương pháp nhiệt
|
Phòng thí nghiệm i |
Mức j |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
4,415 |
9,340 |
17,150** |
19,230** |
24,140 * |
|
2 |
4,130 |
8,375 |
14,460 |
16,140 |
20,155 |
|
3 |
3,700 |
7,500 |
13,600 |
14,800 |
19,500 |
|
4 |
4,100 |
8,865 |
14,400 |
15,550 |
20,300 |
|
5 |
4,005 |
8,005 |
13,825 |
15,660 |
20,705 |
|
6 |
3,890 |
9,000 |
13,980 |
16,500 |
17,570 |
|
7 |
3,750 |
8,150 |
14,150 |
15,450 |
20,100 |
|
8 |
3,905 |
8,055 |
14,840 |
15,315 |
20,940 |
|
9 |
4,045 |
8,305 |
14,170 |
15,290 |
21,185 |
|
* Coi như giá trị tản mạn ** Coi như giá trị bất thường thống kê |
|||||
B.3.3 Trung bình của ô
Trung bình của ô được trình bày trong bảng B.13, theo % khối lượng, với biểu mẫu B của hình 2 (xem 7.2.9).
B.3.4 Độ lệch tuyệt đối trong phạm vi các ô
Độ lệch tuyệt đối trong phạm vi các ô được trình bày trong bảng B.14, ký hiệu là wij , theo % khối lượng, với biểu mẫu c trong hình 2 (xem 7.2.10).
B.3.5 Xem xét sự nhất quán và các giá trị bất thường
Tính các số Mandel h và k (xem 7.3.1) cho các giá trị trong bảng B.7 và B.8. Hàng ngang của bảng thể hiện các chỉ số Mandel tương ứng lấy từ 8.3.
Đồ thị h (hình B.7) chỉ rõ phòng thí nghiệm số 1 đạt được những kết quả thử nghiệm cao hơn nhiều so với những phòng thí nghiệm khác ở cùng mức. Những kết quả như vậy đòi hỏi nhóm trong Hội đồng đang thực hiện việc nghiên cứu liên phòng phải lưu ý. Nếu không tìm được sự lý giải nào cho các kết quả thử nghiệm này thì các thành viên của hội đồng cần đưa ra sự đánh giá của mình dựa trên cơ sở những xem xét bổ sung và phi thống kê để quyết định giữ hay loại bỏ phòng thí nghiệm đó trong việc tính các giá trị độ chụm.
Đồ thị k (hình B.8) chỉ ra sự thay đổi tương đối lớn giữa các kết quả thực nghiệm lặp lại đối với phòng thí nghiệm 6 và 7. Tuy nhiên, những kết quả thử nghiệm này không cho thấy rõ cần có hành động cụ thể nào ngoại trừ việc tìm kiếm những sự lý giải có thể có và, nếu cần thiết, biện pháp xử lý đối với những kết quả thử nghiệm này.
Áp dụng phép kiểm nghiệm Cochran được kết quả sau.
Ở mức 4, độ lệch tuyệt đối 1,10 cho giá trị thống kê thử nghiệm là 1.102/ 1,8149 = 0,667.
Ở mức 5, độ lệch tuyệt đối 1,98 cho giá trị thống kê thử nghiệm là 1,982/6,1663=0,636.
Với p = 9, giá trị tới hạn cho phép kiểm nghiệm Cochran là 0,638 với 5%, và 0,754 với 1%.
Giá trị 1,10 ở mức 4 rõ ràng là một giá trị tản mạn, và giá trị 1,98 ở mức 5 quá gần 5% đến mức cũng có thể là một giá trị tản mạn. Vì hai giá trị trên hoàn toàn khác với tất cả những giá trị khác, và vì sự có mặt của chúng có ảnh hưởng đến số chia dùng số thống kê của phép kiểm nghiệm Cochran nên chúng bị coi là các giá trị tản mạn và được đánh dấu bằng dấu hoa thị. Tuy nhiên không đủ lý lẽ để loại bỏ chúng mặc dù đồ thị số Mandel k cũng làm tăng sự nghi ngờ đối với các giá trị đó.
Áp dụng phép kiểm nghiệm Grubb đối với các giá trị trung bình của ô cho các kết quả trình bày trong bảng B.15.
Với mức 3 và 4. vì phép thử đơn Grubb chỉ ra một giá trị bất thường nên không áp dụng phép thử kép (xem 7.3.4).
Các giá trị trung bình của ô đối với phòng thí nghiệm 1 ở mức 3 và 4 là những giá trị bất thường. Giá trị trung bình của ô đối với phòng thí nghiệm này ở mức 5 cũng cao. Điều này được chỉ ra rõ ràng trên đồ thị số Mandel h (hình B.7).
Tìm hiểu thêm sẽ nhận thấy ít nhất là một trong các mẫu của phòng thí nghiệm 6, mức 5, có thể đến từ mức 4 do nhầm lẫn. Vì độ lệch tuyệt đối ở ô này là đáng nghi ngờ nên đã quyết định là cặp kết quả thử nghiệm này có thể phải loại bỏ. Không dựa vào cặp giá trị đó cũng thấy kết quả thử nghiệm tại phòng thí nghiệm 1 ở mức 5 là đáng nghi ngờ.
Bảng B.14 – Phạm vi ô: Chuẩn độ dầu Creosote bằng phương pháp nhiệt
|
Phòng thí nghiệm i |
Mức j |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
0,05 |
0,00 |
0,50 |
0,00 |
0,28 |
|
2 |
0,20 |
0,09 |
0,08 |
0,16 |
0,49 |
|
3 |
0,00 |
0,20 |
0,00 |
0,60 |
0,40 |
|
4 |
0,00 |
0,13 |
0,40 |
0,10 |
0,00 |
|
5 |
0,07 |
0.23 |
0,19 |
0,24 |
0,35 |
|
6 |
0,28 |
0,48 |
0.16 |
0.16 |
1,98* |
|
7 |
0,10 |
0,30 |
0.10 |
1,10* |
0,80 |
|
8 |
0,01 |
0,03 |
0,00 |
0,19 |
0,32 |
|
9 |
0,05 |
0,27 |
0,14 |
0,30 |
0,95 |
|
* Coi như giá trị tản mạn |
|||||
Vì các kết quả thử nghiệm này đã quyết định loại cặp kết quả thử nghiệm của phòng thí nghiệm 6 mức 5 do không rõ vật liệu gì đã được đo và loại bỏ tất cả các kết quả thử nghiệm của phòng thí nghiệm 1 như là kết quả của một phòng thí nghiệm bất thường.
Bỏ qua những kết quả thử nghiệm này, số thống kê của phép kiểm nghiệm Cochran ở mức 4 sau đó được so sánh với giá trị tới hạn của 8 phòng thí nghiệm (0,680 ở mức 5%). Nó không xuất hiện lâu hơn như là một giá trị tản mạn và đã được giữ lại.
Bảng B.15 – Ứng dụng phép kiểm nghiệm Grubb cho các trung binh ô
|
Mức |
Đơn thấp |
Đơn cao |
Kép thấp |
Kép cao |
Kiểu phép thử |
|
1 |
1,36 |
1,95 |
0,502 |
0,356 |
Phép kiểm nghiệm thống kê Grubb |
|
2 |
1,57 |
1,64 |
0,540 |
0.395 |
|
|
3 |
0.86 |
2,50 |
— |
— |
|
|
4 |
0,91 |
2,47 |
— |
— |
|
|
5 |
1,70 |
2,10 |
0,501 |
0,318 |
|
|
Giá trị tản mạn |
2,215 |
2,215 |
0,149 2 |
0,149 2 |
Giá trị tới hạn Grubb |
|
Giá trị bất thường |
2,387 |
2,387 |
0,085 1 |
0,085 1 |
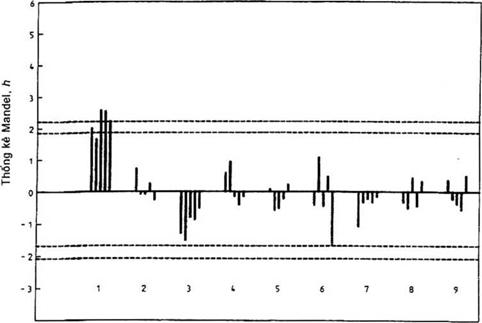
Phòng thí nghiệm i
Hình B.7 – Chuẩn độ dầu creosote: Số thông kê Mandel nhất quán giữa các phòng thí nghiệm, h, được nhóm lại theo các phòng thí nghiệm
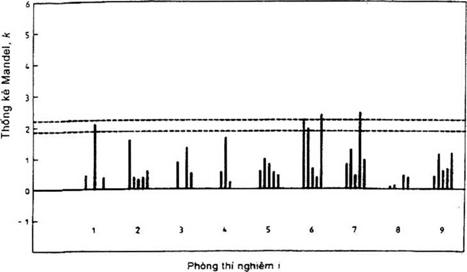
Hình B.8 – Chuẩn độ dầu creosote; số thống kê Mandel nhất quán giữa các phòng thí nghiệm, k, được nhóm lại theo các phòng thí nghiệm
B.3.6 Tính ![]() , srj và sRj
, srj và sRj
Các giá trị ![]() , srj và sRj được tính toán không sử dụng các kết quả thử nghiệm của phòng thí nghiệm 1 và cặp kết quả thử nghiệm của phòng thí nghiệm 6, mức 5, được đưa ra trong bảng B.16, với đơn vị là % của khối lượng, đã được tính toán như trong 7.4.4 và 7.4.5.
, srj và sRj được tính toán không sử dụng các kết quả thử nghiệm của phòng thí nghiệm 1 và cặp kết quả thử nghiệm của phòng thí nghiệm 6, mức 5, được đưa ra trong bảng B.16, với đơn vị là % của khối lượng, đã được tính toán như trong 7.4.4 và 7.4.5.
B.3.7 Sự phụ thuộc của độ chụm vào m
Theo bảng B.16, rõ ràng là độ lệch chuẩn có xu hướng tăng theo các giá trị m, do vậy có thể cho phép thiết lập một dạng nào đó mối quan hệ hàm số. Sự nhìn nhận này được nhà hoá học quen thuộc với phương pháp đo ủng hộ Nhà hóa học cũng cho rằng độ chụm có khả năng phụ thuộc vào mức.
Các tính toán cần thiết để xác định mối quan hệ hàm số không được đưa ra ở đây vì chúng đã được trình bày một cách chi tiết cho sr trong 7.5.9 . Các giá trị sr và sR, được vẽ thành đồ thị theo ![]() trong hình B.9.
trong hình B.9.
Theo hình B.9 rõ ràng là giá trị ở mức 3 rất phân tán và không thể cải thiện bằng bất kỳ quy trình nào khác (xem 7.5.2).
Đối với độ lặp lại, đường thẳng đi qua điểm góc là thỏa đáng.
Đối với độ tái lập, tất cả ba đường đều cho thấy là phù hợp thỏa đáng với số liệu, quan hệ III cho thấy là phù hợp nhất.
Người nào quen thuộc với những yêu cầu của phương pháp đo tiêu chuẩn dành cho dầu creosote có thể lựa chọn mối quan hệ thích hợp nhất.
B.3.8 Các giá trị cuối cùng của độ chụm
Giá trị cuối cùng được làm tròn một cách đúng đắn, phải là:
Độ lệch chuẩn lặp lại sr = 0,019 m
Độ lệch chuẩn tái lập sR = 0,086 + 0,030 m hoặc sR = 0,078 m 0,72
B.3.9 Kết luận
Không có lý do về mặt thống kê nào để ưu tiên một trong hai phương trình đối với sR trong B.3.8. Hội đồng cần quyết định dùng phương trình nào.
Nguyên nhân của các kết quả thử nghiệm bất thường tại phòng thí nghiệm 1 cần được phát hiện.
Thí nghiệm độ chụm này có vẻ như không thỏa đáng. Một trong chín phòng thí nghiệm bị loại bỏ như một giá trị bất thường, một phòng thí nghiệm khác đã thử nghiệm một mẫu sai. Vật liệu cho mức 3 chọn sai, có giá trị gần giống như mức 4 thay vì phải nằm giữa các mức 2 và 4. Hơn thế nữa vật liệu cho mức 3 có vẻ như khác về bản chất, có lẽ thuần khiết hơn so với vật liệu khác. Tốt nhất nên lặp lại thí nghiệm này, với sự cẩn thận hơn khi lựa chọn vật liệu cho các mức khác nhau.
Bảng B.16- Các giá trị tính được của ![]() , srj và sRj cho chuẩn độ dầu creosote bằng phương pháp nhiệt
, srj và sRj cho chuẩn độ dầu creosote bằng phương pháp nhiệt
|
Mức j |
pj |
|
srj |
sRj |
|
1 |
8 |
3,94 |
0,092 |
0,171 |
|
2 |
8 |
8,28 |
0,179 |
0,498 |
|
3 |
8 |
14,18 |
0,127 |
0,400 |
|
4 |
8 |
15,59 |
0,337 |
0,579 |
|
5 |
7 |
20,41 |
0,393 |
0.637 |
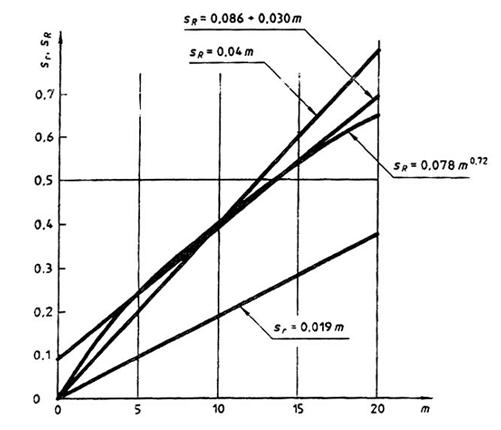
Hình B.9 – Đồ thị của srj và sRj đối với ![]() các số liệu trong bảng B.16, chỉ ra mối quan hệ hàm số thích hợp trong 7.5 từ những số liệu này
các số liệu trong bảng B.16, chỉ ra mối quan hệ hàm số thích hợp trong 7.5 từ những số liệu này
PHỤ LỤC C
(tham khảo)
TÀI LIỆU THAM KHẢO
[1] ISO Guide 33:1989, Uses of certified reference materials
[2] ISO Guide 35:1989. Certification of reference materials – General and statistical principles.
[3] ASTM E691-87. Standard Practice for Conducting an Interlaboratory study to Determine the Precision of a Test Method American Society for Testing and Materials, Philadelphia, PA, USA.
[4] GRUBBS, F.E and BECK, G. Extension of sample sizes and percentage points for significance tests of outlying observations. Technometrics. 14. 1972, pp. 847-854
[5] “Standard Methods for Testing Tar and its Product“. 7th Ed Standardisation of Tar Products Tests Committee. 1979.
[6] TOMKINS, S.S Industrial and Engineering Chemistry (Analytical edition), 14 1942, pp. 141-145.
[7] GRUBBS, F.E Procedures for detecting outlying observations in samples. Technometrics, 11. 1969, pp. 1-21.
[8] ISO 3534-2:1993, Statistics – Vocabulary and symbols – Part 2: Statistical quality control.
[9] ISO 3534-3:1985, Statistics – Vocabulary and symbols – Part 3: Design of experiments
[10] TCVN 6910 – 3 : 2001, Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 3 : Các thước đo trung gian độ chụm của phương pháp đo tiêu chuẩn.
[11] TCVN 6910 – 4 : 2001, Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 4 : Các phương pháp cơ bản xác định độ đúng của phương pháp đo tiêu chuẩn.
[12] TCVN 6910 – 5 : 2002, Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 5 : Các phương pháp khác xác định độ chụm của phương pháp đo tiêu chuẩn.
[13] TCVN 6910 – 6 : 2002, Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 6 : Sử dụng các giá trị độ chính xác trong thực tế.
MỤC LỤC
Lời giới thiệu ……………………………………………………………………………………………..
1. Phạm vi áp dụng ……………………………………………………………………………………..
2. Tiêu chuẩn viện dẫn …………………………………………………………………………………
3. Định nghĩa …………………………………………………………………………………………….
4. Ước lượng các tham số trong mô hình cơ sở ……………………………………………………
5. Yêu cầu đối với thí nghiệm độ chụm ………………………………………………………………
6. Nhân sự trong thí nghiệm độ chụm ………………………………………………………………..
7. Phân tích thống kê thí nghiệm độ chụm……………………………………………………………
7.1. Xem xét ban đầu …………………………………………………………………………………..
7.2. Lập bảng kết quả và ghi chép ……………………………………………………………………
7.3. Khảo sát kết quả về tính nhất quán và các giá trị bất thường ………………………………..
7.3.1. Kỹ thuật nhất quán bằng đồ thị ………………………………………………………………..
7.3.2. Kỹ thuật xử lý giá trị bất thường bằng số …………………………………………………….
7.3.3. Phép kiểm nghiệm Cochran ……………………………………………………………………
7.3.4. Phép kiểm nghiệm Grubb ………………………………………………………………………
7.4. Tính trung bình chung và phương sai …………………………………………………………..
7.5. Thiết lập mối quan hệ hàm số giữa các giá trị độ chụm và mức trung bình m …………….
7.6. Phân tích thống kê theo quy trình từng bước ………………………………………………….
7.7. Báo cáo trình hội đồng và các quyết định của hội đồng ………………………………………
8. Các bảng thống kê …………………………………………………………………………………..
Phụ lục A Các ký hiệu và chữ viết tắt dùng trong TCVN 6910 …………………………………….
Phụ lục B Các ví dụ phân tích thống kê thí nghiệm độ chụm ………………………………………
Phụ lục C Tài liệu tham khảo ……………………………………………………………………………