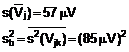Nội dung toàn văn Tiêu chuẩn Việt Nam TCVN 9595-3:2013 (ISO/IEC GUIDE 98-3:2008) về độ không đảm bảo đo – Phần 3: Hướng dẫn trình bày độ không đảm bảo đo (GUM:1995)
TIÊU CHUẨN QUỐC GIA
TCVN 9595-3:2013
ISO/IEC GUIDE 98-3:2008
ĐỘ KHÔNG ĐẢM BẢO ĐO – PHẦN 3: HƯỚNG DẪN TRÌNH BÀY ĐỘ KHÔNG ĐẢM BẢO ĐO (GUM:1995)
Uncertainty of measurement – Part 3: Guide to the expression of uncertainty in measurement (GUM: 1995)
Lời nói đầu
TCVN 9595-3:2013 hoàn toàn tương đương với ISO/IEC Guide 98-3:2008. (GUM:1995)
TCVN 9595-3:2013 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC/M2 Đo lường và các vấn đề liên quan biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ khoa học và Công nghệ công bố.
Bộ tiêu chuẩn TCVN 9595, chấp nhận bộ tiêu chuẩn ISO/IEC Guide 98, gồm các tiêu chuẩn dưới đây có tên chung “Độ không đảm bảo đo”.
– TCVN 9595-1:2013 (ISO/IEC Guide 98-1:2009), Phần 1: Giới thiệu về trình bày độ không đảm bảo đo
– TCVN 9595-3:2013 (ISO/IEC Guide 98-3:2008), Phần 3: Hướng dẫn trình bày độ không đảm bảo đo (GUM:1995).
Bộ tiêu chuẩn ISO/IEC Guide 98 còn có tiêu chuẩn sau:
– ISO/IEC Guide 98-4:2012, Uncertainty of measurement – Part 4; Role of measurement uncertainty in conformity assessment.
Lới giới thiệu
0.1. Khi báo cáo kết quả đo một đại lượng vật lý, phải đưa ra chỉ số định lượng cho chất lượng của kết quả để người sử dụng có thể đánh giá độ tin cậy của kết quả. Không có chỉ số này, các kết quả đo không thể so sánh được với nhau hoặc với các giá trị quy chiếu được nêu trong quy định kỹ thuật hoặc tiêu chuẩn. Do đó, cần có một thủ tục, dễ áp dụng, dễ hiểu và được chấp nhận chung để mô tả đặc trưng chất lượng của kết quả đo, để đánh giá và trình bày độ không đảm bảo của nó.
0.2. Khái niệm độ không đảm bảo như thuộc tính có thể định lượng là tương đối mới trong lịch sử đo lường dù sai số và phân tích sai số từ lâu đã là một phần của thực hành khoa học phép đo hoặc đo lường học. Thực tế là khi tất cả các thành phần sai số đã biết hoặc nghi ngờ được đánh giá và được hiệu chỉnh phù hợp thì vẫn còn độ không đảm bảo về tính chính xác của kết quả được nêu, nghĩa là nghi ngờ về mức độ của kết quả đo đại diện cho giá trị của đại lượng được đo.
0.3. Cũng giống như việc sử dụng gần như toàn cầu hệ đơn vị quốc tế (SI) đã mang lại sự nhất quán cho tất cả phép đo khoa học và công nghệ, sự đồng thuận toàn cầu về đánh giá và trình bày độ không đảm bảo đo sẽ cho phép ý nghĩa của phổ rộng các kết quả đo trong khoa học, kỹ thuật, thương mại, công nghiệp và quy định dễ hiểu và được giải thích thích đáng. Trong thời đại thị trường toàn cầu này, phương pháp đánh giá và trình bày độ không đảm bảo cần đồng nhất trên khắp thế giới nhờ đó các phép đo được thực hiện ở các quốc gia khác nhau có thể được so sánh dễ dàng.
0.4. Phương pháp lý tưởng đối với đánh giá và trình bày độ không đảm bảo của kết quả đo cần:
– phổ quát: phương pháp có thể áp dụng cho tất cả các loại phép đo và tất cả các loại dữ liệu đầu vào được sử dụng trong phép đo.
Đại lượng thực tế được sử dụng để trình bày độ không đảm bảo cần:
– nhất quán nội tại: nó cần được suy luận trực tiếp từ các thành phần đóng góp vào độ không đảm bảo, cũng như không phụ thuộc vào cách các thành phần này được nhóm và sự phân tách các thành phần thành các thành phần con;
– có thể chuyển giao: có thể sử dụng trực tiếp độ không đảm bảo được đánh giá cho một kết quả như thành phần trong việc đánh giá độ không đảm bảo của phép đo khác có sử dụng kết quả đầu tiên.
Ngoài ra, trong nhiều ứng dụng công nghiệp và thương mại, cũng như trong lĩnh vực sức khỏe và an toàn, thường cần đưa ra một khoảng kết quả đo có thể kỳ vọng bao hàm phần lớn sự phân bố các giá trị có thể được quy cho đại lượng được đo. Do đó, phương pháp ý tưởng đối với đánh giá và trình bày độ không đảm bảo trong đo lường cần có khả năng sẵn sàng cung cấp khoảng đó, cụ thể là, khoảng có xác suất phủ hoặc mức tin cậy trong thực tế phù hợp với yêu cầu.
0.5. Cách tiếp cận là cơ sở của tiêu chuẩn này là cách tiếp cận được nêu trong Khuyến nghị INC-1 (1980) [2] của nhóm công tác về Trình bày độ không đảm bảo, do BIPM triệu tập theo yêu cầu của CIPM. Cách tiếp cận này và, lý giải của nó được thảo luận trong Phụ lục E, đáp ứng tất cả các yêu cầu nêu trên. Đây không phải trường hợp cho hầu hết các phương pháp khác sử dụng hiện nay. Khuyến nghị INC-1 (1980) được CIPM thông qua và xác nhận lại trong các Khuyến nghị 1 (CI-1981) [3] và 1 (CI-1986) [4]; các khuyến nghị CIPM này được nêu lại trong Phụ lục A (xem A.2 và A.3). Vì khuyến nghị INC-1 (1980) là nền móng cho tiêu chuẩn này nên nội dung được nêu lại trong 0.7.
0.6. Bản tổng kết ngắn gọn thủ tục được quy định trong tiêu chuẩn này đối với đánh giá và trình bày độ không đảm bảo đo được nêu trong Điều 8 và một số ví dụ trình bày chi tiết trong Phụ lục H. Các phụ lục khác đưa ra các thuật ngữ chung trong đo lường (Phụ lục B); thuật ngữ và khái niệm thống kê cơ bản (Phụ lục C); giá trị “thực”, sai số và độ không đảm bảo (Phụ lục D); các gợi ý thực hành đối với đánh giá các thành phần độ không đảm bảo (Phụ lục F); bậc tự do và mức tin cậy (Phụ lục G); các ký hiệu toán hoàn chỉnh được sử dụng trong tiêu chuẩn này (Phụ lục J); và Tài liệu tham khảo. Tiêu chuẩn còn có một mục lục tra cứu theo bảng chữ cái.
0.7. Khuyến nghị INC-1 (1980) Trình bày độ không đảm bảo thực nghiệm
1) Độ không đảm bảo trong kết quả đo thường gồm các thành phần khác nhau có thể được nhóm thành hai loại theo cách các trị số của chúng được ước lượng:
A. Các thành phần được đánh giá bằng các phương pháp thống kê,
B. Các thành phần được đánh giá bằng các công cụ khác.
Không phải lúc nào cũng có sự phù hợp tuyệt đối giữa việc phân loại thành nhóm A hay B và trước đây sử dụng cách phân loại là độ không đảm bảo “ngẫu nhiên” và “hệ thống”. Thuật ngữ “độ không đảm bảo hệ thống” có thể bị hiểu sai lệch và cần tránh.
Mọi báo cáo chi tiết về độ không đảm bảo bao gồm danh sách đầy đủ các thành phần, cụ thể cho từng phương pháp được sử dụng để nhận được trị số của nó.
2) Các thành phần thuộc nhóm A cần được đặc trưng bởi phương sai ước lượng ![]() , (hoặc “độ lệch chuẩn” ước lượng si) và số bậc tự do vi. Cần đưa ra các hiệp phương sai khi thích hợp.
, (hoặc “độ lệch chuẩn” ước lượng si) và số bậc tự do vi. Cần đưa ra các hiệp phương sai khi thích hợp.
3) Các thành phần thuộc nhóm B cần được đặc trưng bởi các đại lượng ![]() , có thể được coi là xấp xỉ với phương sai tương ứng, giả định là tồn tại. Các đại lượng
, có thể được coi là xấp xỉ với phương sai tương ứng, giả định là tồn tại. Các đại lượng ![]() có thể được xử lý giống như phương sai và đại lượng uj giống như độ lệch chuẩn. Các hiệp phương sai cần được xử lý theo cách tương tự, khi thích hợp.
có thể được xử lý giống như phương sai và đại lượng uj giống như độ lệch chuẩn. Các hiệp phương sai cần được xử lý theo cách tương tự, khi thích hợp.
4) Độ không đảm bảo tổng hợp cần được đặc trưng bởi trị số nhận được bằng cách áp dụng phương pháp thường dùng đối với tổ hợp phương sai. Độ không đảm bảo tổng hợp và các thành phần của nó cần được thể hiện ở dạng “độ lệch chuẩn”.
5) Đối với các ứng dụng cụ thể, nếu cần nhân độ không đảm bảo tổng hợp với một thừa số để nhận được độ không đảm bảo tổng thể thì luôn phải quy định thừa số nhân được sử dụng.
ĐỘ KHÔNG ĐẢM BẢO ĐO – PHẦN 3: HƯỚNG DẪN TRÌNH BÀY ĐỘ KHÔNG ĐẢM BẢO ĐO (GUM:1995)
Uncertainty of measurement – Part 3: Guide to the expression of uncertainty in measurement (GUM: 1995)
1. Phạm vi áp dụng
1.1. Tiêu chuẩn này thiết lập các quy tắc chung về đánh giá và trình bày độ không đảm bảo đo có thể tuân theo ở các cấp độ chính xác khác nhau và trong nhiều lĩnh vực – từ mặt hàng nhà xưởng đến nghiên cứu cơ bản. Do đó, các nguyên tắc của tiêu chuẩn này được dự kiến áp dụng nhiều loại phép đo, bao gồm các phép đo được yêu cầu đối với:
– duy trì kiểm soát chất lượng và đảm bảo chất lượng trong sản xuất;
– tuân thủ luật và quy định đang có hiệu lực;
– thực hiện nghiên cứu cơ bản, nghiên cứu ứng dụng và triển khai trong khoa học và kỹ thuật;
– hiệu chuẩn các chuẩn và phương tiện và thực hiện các phép thử cho toàn bộ hệ đo lường quốc gia để đạt được tính liên kết chuẩn với các chuẩn quốc gia;
– xây dựng, duy trì và so sánh các chuẩn chính vật lý quốc gia và quốc tế bao gồm cả mẫu chuẩn.
1.2. Tiêu chuẩn này chủ yếu đề cập tới việc trình bày độ không đảm bảo đo của đại lượng vật lý được xác định rõ ràng – đại lượng đo – có thể được đặc trưng bằng một giá trị cơ bản duy nhất. Nếu hiện tượng quan tâm chỉ có thể được thể hiện như một phân bố các giá trị hoặc phụ thuộc vào một hoặc nhiều tham số, như thời gian, thì các đại lượng đo được yêu cầu đối với việc mô tả là tập hợp các đại lượng mô tả phân bố hoặc sự phụ thuộc đó.
1.3. Tiêu chuẩn này cũng có thể áp dụng để đánh giá và trình bày độ không đảm bảo gắn với thiết kế về khái niệm và các phân tích thực nghiệm lý thuyết, phương pháp đo, các thành phần và hệ thống phức tạp. Vì kết quả đo và độ không đảm bảo của nó có thể là khái niệm và hoàn toàn dựa trên dữ liệu giả thiết nên thuật ngữ “kết quả đo” được dùng trong tiêu chuẩn này cần được hiểu trong ngữ cảnh rộng hơn.
1.4. Tiêu chuẩn này cung cấp các quy tắc chung để đánh giá và trình bày độ không đảm bảo đo hơn là các chỉ dẫn cụ thể, đặc trưng công nghệ. Ngoài ra, tiêu chuẩn không thảo luận cách thức độ không đảm bảo của kết quả đo cụ thể, khi được đánh giá, có thể được sử dụng cho các mục đích khác, ví dụ, đưa ra kết luận về khả năng tương thích của kết quả đó với các kết quả tương tự khác, thiết lập các giới hạn dung sai trong quá trình sản xuất, hoặc quyết định liệu một quá trình hành động nào đó có thể đảm bảo an toàn không. Do đó cần xây dựng các tiêu chuẩn cụ thể dựa trên tiêu chuẩn này nhằm giải quyết các vấn đề nhất định cho các lĩnh vực đo lường cụ thể hoặc sử dụng các cách thể hiện định lượng độ không đảm bảo khác nhau. Các tiêu chuẩn đó có thể là các phiên bản đơn giản hóa các tiêu chuẩn này nhưng cần bao gồm các chi tiết phù hợp với mức độ chính xác, độ phức tạp của phép đo và việc sử dụng được hướng tới.
CHÚ THÍCH: Có thể có các tình huống trong đó khái niệm độ không đảm bảo của phép đo được tin là không có khả năng áp dụng đầy đủ, ví dụ như khi xác định độ chụm của một phương pháp thử (xem ví dụ ở tài liệu tham khảo [5]).
2. Thuật ngữ và định nghĩa
2.1. Thuật ngữ chung về đo lường
Định nghĩa một số thuật ngữ chung về đo lường liên quan với tiêu chuẩn này, như “đại lượng đo lường” “đại lượng đo” và “sai số của phép đo”, được nêu trong Phụ lục B. Các định nghĩa này được lấy từ Từ vựng quốc tế về thuật ngữ chung và cơ bản trong đo lường học (viết tắt là VIM) [6]*. Ngoài ra, Phụ lục C đưa ra các định nghĩa về một số thuật ngữ thống kê cơ bản chủ yếu lấy từ tiêu chuẩn TCVN 8244-1 (ISO 3534-1) [7]. Khi một trong các thuật ngữ đo lường hoặc thống kê (hoặc thuật ngữ liên quan chặt chẽ) được sử dụng lần đầu trong văn bản, bắt đầu với Điều 3, nó được in chữ đậm và điều định nghĩa được đặt trong dấu ngoặc đơn.
Do tầm quan đối với tiêu chuẩn này, định nghĩa về thuật ngữ đo lường chung “độ không đảm bảo đo” được nêu trong cả Phụ lục B và 2.2.3. Các định nghĩa về các thuật ngữ quan trọng nhất cụ thể với tiêu chuẩn này được nêu trong 2.3.1 đến 2.3.6. Trong tất cả các điều này và trong Phụ lục B và C, có thể không sử dụng dấu ngoặc đơn cho một số thuật ngữ cụ thể nếu không gây nhầm lẫn.
2.2. Thuật ngữ “độ không đảm bảo”
Khái niệm độ không đảm bảo được đề cập nhiều hơn trong Điều 3 và Phụ lục D.
2.2.1. Từ “độ không đảm bảo” nghĩa là nghi ngờ và do đó theo nghĩa rộng nhất của nó, “độ không đảm bảo đo” có nghĩa là nghi ngờ về hiệu lực của kết quả đo. Vì không có từ khác cho khái niệm chung về độ không đảm bảo này và các đại lượng cụ thể cung cấp thước đo định lượng của khái niệm, ví dụ, độ lệch chuẩn, nên cần sử dụng từ “độ không đảm bảo” theo hai nghĩa khác nhau này.
2.2.2. Trong tiêu chuẩn này, từ “độ không đảm bảo” không đi cùng tính từ nói đến khái niệm chung của độ không đảm bảo và một hoặc tất cả các thước đo định lượng của khái niệm đó. Khi một thước đo cụ thể được ấn định thì tính từ thích hợp được sử dụng.
2.2.3. Định nghĩa chính thức cho thuật ngữ “độ không đảm bảo của phép đo” được xây dựng để sử dụng trong tiêu chuẩn này và trong VIM [6] (VIM: 1993, định nghĩa 3.9) như sau:
Độ không đảm bảo (của phép đo)
Tham số, gắn với kết quả đo, đặc trưng cho sự phân tán của các giá trị có thể được quy cho đại lượng đo một cách hợp lý.
CHÚ THÍCH 1: Tham số có thể là, ví dụ, độ lệch chuẩn (hoặc một bội xác định của nó), hoặc nửa của khoảng, với mức tin cậy quy định.
CHÚ THÍCH 2: Nói chung, độ không đảm bảo đo bao gồm nhiều thành phần. Một số thành phần có thể đánh giá bằng phân bố thống kê của các kết quả từ dãy các phép đo và có thể được đặc trưng bằng độ lệch chuẩn thực nghiệm. Các thành phần khác, cũng có thể được đặc trưng bằng độ lệch chuẩn, được đánh giá từ phân bố xác suất giả định dựa trên thực nghiệm hoặc thông tin khác.
CHÚ THÍCH 3: Kết quả đo là ước lượng tốt nhất của giá trị đại lượng đo và tất cả thành phần của độ không đảm bảo, gồm cả các thành phần xuất hiện từ những tác động hệ thống như thành phần gắn với sự hiệu chính và chuẩn đo lường, đều góp phần vào sự phân tán.
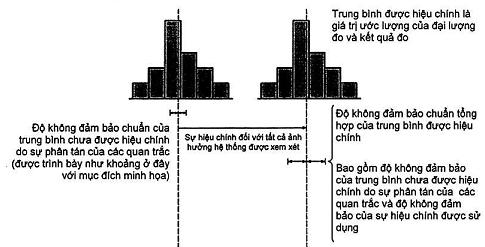
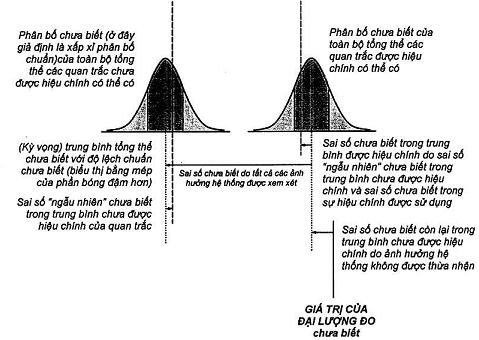
2.2.4. Định nghĩa về độ không đảm bảo của phép đo được nêu trong 2.2.3 là định nghĩa toán tử tập trung vào kết quả đo và độ không đảm bảo được đánh giá của nó. Tuy nhiên, nó không mâu thuẫn với các khái niệm khác về độ không đảm bảo đo, như:
– thước đo của sai số có thể có trong giá trị ước lượng của đại lượng đo như được cung cấp bởi kết quả của một phép đo;
– ước lượng xác định đặc trưng dãy giá trị trong đó chứa giá trị thực của đại lượng đo (VIM: 1984, định nghĩa 3.09).
Mặc dù hai khái niệm truyền thống này là đúng như là lý tưởng nhưng chúng tập trung tương ứng vào các đại lượng không thể biết được tương ứng:” sai số” của kết quả đo và “giá trị thực” của đại lượng đo (trái ngược với giá trị ước lượng). Tuy nhiên, bất kỳ khái niệm về độ không đảm bảo nào được chọn thì thành phần độ không đảm bảo luôn được đánh giá bằng cách sử dụng cùng dữ liệu và thông tin liên quan (Xem thêm E.5).
2.3. Thuật ngữ riêng của tiêu chuẩn này
Nói chung, các thuật ngữ riêng của tiêu chuẩn này sẽ được định nghĩa trong phần lời khi được nhắc đến lần đầu. Tuy nhiên, định nghĩa của các thuật ngữ quan trọng nhất được nêu ở đây để dễ tham khảo.
CHÚ THÍCH: Mô tả rõ hơn liên quan tới các thuật ngữ này có thể tìm được như sau: đối với 2.3.2, xem 3.3.3 và 4.2; đối với 2.3.3, xem 3.3.3 và 4.3; đối với 2.3.4, xem Điều 5 và Phương trình (10) và (13); và đối với 2.3.5 và 2.3.6, xem Điều 6.
2.3.1. Độ không đảm bảo chuẩn (standard uncertainty)
Độ không đảm bảo của kết quả đo được thể hiện như là độ lệch chuẩn.
2.3.2. Đánh giá loại A (của độ không đảm bảo) [Type A evaluation (of uncertainty)]
Phương pháp đánh giá độ không đảm bảo bằng phân tích thống kê các dãy quan trắc.
2.3.3. Đánh giá loại B (của độ không đảm bảo) [Type B evaluation (of uncertainty)]
Phương pháp đánh giá độ không đảm bảo bằng các cách khác với phân tích thống kê các dãy quan trắc.
2.3.4. Độ không đảm bảo chuẩn tổng hợp (combined standard uncertainty)
Độ không đảm bảo chuẩn của kết quả đo khi kết quả đó nhận được từ các giá trị của một số đại lượng đầu vào, bằng dương căn bậc hai tổng các số hạng. Các số hạng này là phương sai hoặc hiệp phương sai của các đại lượng đầu vào này được lấy trọng số theo các kết quả đo biến động theo sự thay đổi trong các đại lượng này.
2.3.5. Độ không đảm bảo mở rộng (expanded uncertainty)
Đại lượng xác định khoảng kết quả đo có thể được kỳ vọng phủ phần lớn phân bố các giá trị có thể quy cho đại lượng đo một cách hợp lý.
CHÚ THÍCH 1: Phần này có thể xem là xác suất phủ hoặc mức tin cậy của khoảng.
CHÚ THÍCH 2: Để kết hợp mức tin cậy cụ thể với khoảng được xác định bằng độ không đảm bảo đo mở rộng cần các giả thiết rõ ràng hoặc ngụ ý về phân bố xác suất đặc trưng bằng kết quả đo và độ không đảm bảo đo chuẩn tổng hợp. Mức tin cậy có thể quy cho khoảng này chỉ có thể được biết ở mức độ các giả thiết kể trên được chứng minh.
CHÚ THÍCH 3: Độ không đảm bảo mở rộng được gọi là độ không đảm bảo toàn thể ở đoạn 5 của Khuyến nghị INC-1 (1980).
2.3.6. Hệ số phủ (coverage factor)
Thừa số được dùng để nhân với độ không đảm bảo chuẩn tổng hợp để nhận được độ không đảm bảo mở rộng.
CHÚ THÍCH: Hệ số phủ, k, thường nằm trong khoảng từ 2 đến 3.
3. Các khái niệm cơ bản
Phần đề cập thêm về các khái niệm cơ bản có thể xem trong Phụ lục D, tập trung vào khái niệm giá trị “thực”, sai số và độ không đảm bảo, bao gồm các minh họa bằng đồ thị các khái niệm này; trong Phụ lục E, khảo sát động lực và cơ sở thống kê đối với Khiếu nghị INC-1 (1980) mà tiêu chuẩn này dựa vào. Phụ lục J là bằng chú giải các ký hiệu toán học chính được dùng trong tiêu chuẩn này.
3.1. Phép đo
3.1.1. Mục đích của phép đo (B.2.5) là để xác định giá trị (B.2.2) của đại lượng đo (B.2.9), đó là giá trị của đại lượng cụ thể (B.2.1, Chú thích 1) cần đo. Do đó, phép đo bắt đầu với quy định kỹ thuật phù hợp với đại lượng đo, phương pháp đó (B.2.7) và thủ tục đo (B.2.8).
CHÚ THÍCH: Thuật ngữ “giá trị thực” (xem Phụ lục D) không được sử dụng trong tiêu chuẩn này ví lý do được nêu trong D.3.5; thuật ngữ “giá trị của đại lượng đo” (hoặc của đại lượng) và “giá trị thực của đại lượng đo” (hoặc của đại lượng) được xem là tương đương nhau.
3.1.2. Nói chung, kết quả đo (B.2.11) chỉ là gần đúng hoặc ước lượng (C.2.26) của giá trị đại lượng đo và do đó chỉ đầy đủ khi làm theo tuyên bố về độ không đảm bảo (B.2.18) của ước lượng đó.
3.1.3. Trong thực tế, quy định cần thiết hoặc định nghĩa đại lượng đo chịu sự chi phối yêu cầu của độ chính xác của phép đo (B.2.14). Đại lượng đo cần được xác định hoàn chỉnh theo độ chính xác yêu cầu để tất cả các mục đích thực tế gắn với phép đo giá trị của nó là duy nhất. Cách trình bày “giá trị của đại lượng đo” sử dụng trong tiêu chuẩn này theo ý nghĩa như trên.
VÍ DỤ: Nếu độ dài của một thanh thép dài một-mét danh nghĩa được xác định với độ chính xác đến micrômét thì quy định kỹ thuật cần bao gồm nhiệt độ và áp suất tại đó chiều dài đó được xác định. Do đó, đại lượng đo cần được quy định là, ví dụ, độ dài của thanh ở 25,000C và 101 325 Pa (kể cả các tham số xác định khác được coi là cần thiết, như cách thanh thép được đỡ). Tuy nhiên, nếu chiều dài được xác định chỉ với độ chính xác đến milimét thì quy định kỹ thuật không yêu cầu nhiệt độ và áp suất xác định hoặc giá trị tham số xác định khác.
CHÚ THÍCH: Việc xác định không đầy đủ đại lượng đo có thể gây ra thành phần độ không đảm bảo đủ lớn phải được tính đến khi đánh giá độ không đảm bảo của kết quả đo (xem D.1.1, D.3.4 và D.6.2).
3.1.4. Trong nhiều trường hợp, kết quả đo được xác định trên cơ sở các dãy quan trắc nhận được dưới các điều kiện lặp lại (B.2.15, Chú thích 1).
3.1.5. Giả định có độ biến động trong các quan trắc lặp lại vì đại lượng ảnh hưởng (B.2.10) có thể ảnh hưởng đến kết quả đo không duy trì ổn định hoàn toàn.
3.1.6. Mô hình toán của phép đo chuyển tập hợp các quan trắc lặp lại thành kết quả đo có tầm quan trọng quyết định vì, cùng với các quan trắc, nó thường bao gồm nhiều đại lượng ảnh hưởng chưa được biết chính xác. Sự thiếu hiểu biết này góp phần vào độ không đảm bảo của kết quả đo, cũng như độ biến động của các quan trắc lặp lại và mọi độ không đảm bảo gắn với chính mô hình toán đó.
3.1.7. Tiêu chuẩn này coi đại lượng đo như đại lượng vô hướng (đại lượng đơn lẻ). Việc mở rộng ra tập hợp các đại lượng đo liên quan xác định đồng thời trong cùng một phép đo đòi hỏi phải thay thế đại lượng đo vô hướng và phương sai (C.2.11, C.2.20, C.3.2) của nó bằng đại lượng véc tơ và ma trận hiệp phương sai (C.3.5). Sự thay thế như vậy chỉ được xem xét trong tiêu chuẩn này ở các ví dụ (xem H.2, H.3 và H.4).
3.2. Sai số, ảnh hưởng và hiệu chỉnh
3.2.1. Nói chung, phép đo có sự không hoàn chỉnh gây ra sai số (B.2.19) trong kết quả đo. Thông thường, sai số được xem là có hai thành phần, đó là, thành phần ngẫu nhiên (B.2.21) và thành phần hệ thống (B.2.22).
CHÚ THÍCH: Sai số là một khái niệm lý tưởng hóa và sai số không thể được biết chính xác.
3.2.2. Sai số ngẫu nhiên có thể xuất hiện từ các biến động không dự đoán được hoặc sự biến động thời gian và không gian ngẫu nhiên của các đại lượng ảnh hưởng. Ảnh hưởng của các biến động như vậy, sau đây gọi là ảnh hưởng hỗn loạn, làm tăng độ biến động trong các quan trắc lặp lại của đại lượng đo. Mặc dù không thể bù cho sai số ngẫu nhiên của kết quả đo nhưng thường có thể giảm bớt bằng cách tăng số quan trắc; kỳ vọng hoặc giá trị được kỳ vọng (C.2.9, C.3.1) của sai số ngẫu nhiên bằng “không”.
CHÚ THÍCH 1: Độ lệch chuẩn thực hiện của trung bình cộng hoặc trung bình của dãy các quan trắc (xem 4.2.3) không phải là sai số ngẫu nhiên của trung bình, mặc dù nó được gọi như vậy trong một số ấn phẩm. Nó được thay bằng thước đo độ không đảm bảo trung bình do các ảnh hưởng ngẫu nhiên. Không thể biết chính xác giá trị của sai số trong trung bình gây ra bởi các ảnh hưởng này.
CHÚ THÍCH 2: Trong tiêu chuẩn này cần chú ý phân biệt các thuật ngữ “sai số” và “độ không đảm bảo”. Chúng không phải là từ đồng nghĩa mà các thuật ngữ này đại diện cho các khái niệm hoàn toàn khác nhau; không nên nhầm lẫn hoặc sử dụng lại.
3.2.3. Sai sót hệ thống, giống như sai số ngẫu nhiên, không thể loại trừ được nhưng thường cũng có thể giảm bớt. Nếu sai số hệ thống phát sinh do tác động của đại lượng ảnh hưởng đã biết tới kết quả đo, sau đây gọi là ảnh hưởng hệ thống, thì ảnh hưởng đó có thể được định lượng và, nếu có độ lớn đáng kể so với độ chính xác của phép đo yêu cầu, thì sự hiệu chỉnh (B.2.23) hoặc thừa số hiệu chỉnh (B.2.24) có thể được sử dụng để bù cho ảnh hưởng đó. Giả định rằng, sau khi hiệu chính, kỳ vọng hoặc giá trị kỳ vọng của sai số phát sinh từ ảnh hưởng hệ thống bằng “không”.
CHÚ THÍCH: Độ không đảm bảo của sự hiệu chính áp dụng cho kết quả đo để bù cho ảnh hưởng hệ thống không phải là sai số hệ thống, thường được gọi là độ chệch, trong kết quả đo do ảnh hưởng đó như đôi khi nó được gọi. Nó thay thế cho thước đo độ không đảm bảo của kết quả do sự hiểu biết không đầy đủ về giá trị hiệu chính yêu cầu. Sai số xuất hiện từ việc bù không hoàn toàn ảnh hưởng hệ thống không thể biết chính xác. Thuật ngữ “sai số” và “độ không đảm bảo” cần được sử dụng đúng đắn và cẩn thận để phân biệt chúng.
3.2.4. Giả định rằng kết quả đo đã được hiệu chính đối với tất cả ảnh hưởng hệ thống đáng kể đã biết và mọi nỗ lực đã được thực hiện để xác định các ảnh hưởng đó.
VÍ DỤ: Sự hiệu chính do trở kháng hữu hạn của vôn kế được sử dụng để xác định hiệu điện thế (đại lượng đo) qua điện trở trở kháng cao được áp dụng để giảm ảnh hưởng hệ thống lên kết quả đo xuất hiện từ hiệu ứng tải của vôn kế. Tuy nhiên, bản thân giá trị trở kháng của vôn kế và điện trở, được dùng để ước lượng giá trị hiệu chính và nhận được từ các phép đo khác nhau, là không đảm bảo. Các độ không đảm bảo này được sử dụng để đánh giá thành phần độ không đảm bảo của việc xác định hiệu điện thế xuất hiện từ sự hiệu chính và do đó từ ảnh hưởng hệ thống do trở kháng hữu hạn của vôn kế.
CHÚ THÍCH 1: Thông thường, các phương tiện do và hệ thống đo được hiệu chỉnh hoặc hiệu chuẩn bằng cách sử dụng các chuẩn đo lường và mẫu chuẩn để loại trừ các ảnh hưởng hệ thống; tuy nhiên, độ không đảm bảo gắn với các chuẩn và vật liệu này vẫn phải được tính đến.
CHÚ THÍCH 2: Trường hợp không áp dụng sự hiệu chính đối với ảnh hưởng hệ thống quan trọng đã biết được đề cập trong Chú thích của 6.3.1 và trong F.2.4.5.
3.3. Độ không đảm bảo
3.3.1. Độ không đảm bảo của kết quả đo phản ánh sự thiếu hiểu biết chính xác về giá trị của đại lượng đo (xem 2.2). Kết quả đo sau hiệu chính đối với các ảnh hưởng hệ thống được thừa nhận vẫn chỉ là ước lượng giá trị của đại lượng đo vì độ không đảm bảo xuất hiện từ các ảnh hưởng ngẫu nhiên và từ sự hiệu chính kết quả không hoàn chỉnh đối với ảnh hưởng hệ thống.
CHÚ THÍCH: Kết quả đo (sau hiệu chính) có thể không nhận biết được là rất gần với giá trị của đại lượng đo (và do đó có sai số không đáng kể) mặc dù có thể có độ không đảm bảo lớn. Do đó không nên nhầm độ không đảm bảo của kết quả đo với sai số chưa biết còn lại.
3.3.2. Trong thực tế, có nhiều nguồn độ không đảm bảo có thể có trong phép đo, bao gồm:
a) sự định nghĩa không đầy đủ về đại lượng đo;
b) sự nhận thức không hoàn chỉnh về định nghĩa đại lượng đo;
c) sự lấy mẫu không đại diện – mẫu được đo có thể không đại diện cho đại lượng đo đã xác định;
d) thiếu sự hiểu biết về ảnh hưởng của điều kiện môi trường tới phép đo hoặc phép đo điều kiện môi trường không hoàn hảo;
e) độ chệch của người đo khi đọc phương tiện đo chỉ thị tương tự;
f) độ phân giải của phương tiện đo hoặc ngưỡng nhận biết có giới hạn;
g) giá trị không chính xác của chuẩn đo lường và mẫu chuẩn;
h) giá trị không chính xác của hằng số và các tham số khác nhận được từ nguồn bên ngoài và được sử dụng trong thuật toán rút gọn dữ liệu;
i) phép tính gần đúng và giả định được tích hợp trong phương pháp và thủ tục đo;
j) độ biến động trong các quan trắc lặp lại của đại lượng đo trong điều kiện bên ngoài như nhau.
Các nguồn này không nhất thiết phải độc lập, và một số nguồn từ a) đến i) có thể đóng góp cho nguồn j). Tất nhiên, ảnh hưởng hệ thống không được thừa nhận không thể được tính đến trong việc đánh giá độ không đảm bảo của kết quả đo nhưng vẫn đóng góp vào sai số đo.
3.3.3. Khuyến nghị INC-1 (1980) của Nhóm công tác về trình bày độ không đảm bảo chia các thành phần độ không đảm bảo thành hai nhóm dựa trên phương pháp đánh giá, “A” và “B” (xem 0.7, 2.3.2 và 2.3.3). Các nhóm này áp dụng cho độ không đảm bảo và không thay cho từ “ngẫu nhiên” và “hệ thống”. Trong một số trường hợp độ không đảm bảo của sự hiệu chính đối với ảnh hưởng hệ thống đã biết có thể nhận được bằng đánh giá Loại A trong khi ở trường hợp khác là bằng đánh giá Loại B, vì có thể độ không đảm bảo đặc trưng cho ảnh hưởng ngẫu nhiên.
CHÚ THÍCH: Trong một số tiêu chuẩn, các thành phần của độ không đảm bảo được phân loại thành “ngẫu nhiên” và “hệ thống” và gắn với các sai số xuất hiện từ các ảnh hưởng ngẫu nhiên và ảnh hưởng hệ thống đã biết tương ứng. Sự phân loại các thành phần của độ không đảm bảo như vậy có thể mơ hồ khi được áp dụng rộng rãi. Ví dụ, thành phần “ngẫu nhiên” của độ không đảm bảo trong một phép đo có thể trở thành thành phần “hệ thống” của độ không đảm bảo trong phép đo khác trong đó kết quả đo đầu tiên được sử dụng làm dữ liệu đầu vào. Phân loại các phương pháp đánh giá thành phần độ không đảm bảo hơn là phân loại bản thân các thành phần sẽ tránh được sự mơ hồ này. Đồng thời, không loại trừ việc thu thập các thành phần riêng lẻ đã được đánh giá bởi hai phương pháp khác nhau thành các nhóm được ấn định để sử dụng cho một mục đích cụ thể (xem 3.4.3).
3.3.4. Mục đích của việc phân loại thành Loại A và Loại B là để chỉ ra hai cách đánh giá thành phần độ không đảm bảo khác nhau và chỉ để tạo thuận lợi cho thảo luận; việc phân loại này không có nghĩa là có bất kỳ sự khác biệt nào về bản chất của các thành phần do hai loại đánh giá gây nên. Cả hai loại đánh giá dựa trên phân bố xác suất (C.2.3), và các thành phần độ không đảm bảo gây ra do một trong hai loại được định lượng bởi các phương sai hoặc độ lệch chuẩn.
3.3.5. Phương sai ước lượng u2 đặc trưng cho thành phần độ không đảm bảo nhận được từ đánh giá Loại A được tính toán từ dãy các quan trắc lặp lại và là phương sai ước lượng thống kê quen thuộc s2 (xem 4.2). Độ lệch chuẩn (C.2.12, C.2.21, C.3.3) ước lượng u, dương căn bậc hai của u2, do đó bằng u = s và để thuận tiện đôi khi được gọi là độ không đảm bảo chuẩn Loại A. Đối với thành phần độ không đảm bảo nhận được từ đánh giá Loại B, phương sai ước lượng u2 được đánh giá bằng cách sử dụng sự hiểu biết có sẵn (xem 4.3) và độ lệch chuẩn ước lượng u đôi khi được gọi là độ không đảm bảo chuẩn Loại B.
Do đó độ không đảm bảo chuẩn Loại A nhận được từ hàm mật độ xác suất (C.2.5) được suy ra từ phân bố tần suất quan trắc được (C.2.18), trong khi độ không đảm bảo chuẩn Loại B nhận được từ hàm mật độ xác suất giả định dựa trên sự tin tưởng rằng một biến cố sẽ xảy ra [thường được gọi là xác suất (C.2.1) chủ quan]. Cả hai cách tiếp cận đều sử dụng cách giải thích xác suất được thừa nhận.
CHÚ THÍCH: Đánh giá Loại B thành phần độ không đảm bảo thường dựa trên tổ hợp thông tin tương đối tin cậy có thể so sánh được (xem 4.3.1).
3.3.6. Độ không đảm bảo chuẩn của kết quả đo, khi kết quả đo nhận được từ các giá trị của một số đại lượng khác, được gọi là độ không đảm bảo chuẩn tổng hợp và được ký hiệu là uc. Độ lệch chuẩn ước lượng gắn với kết quả và bằng dương căn bậc hai của phương sai tổng hợp nhận được từ tất cả các thành phần phương sai và hiệp phương sai (C.3.4), dù đã được đánh giá, bằng cách sử dụng định luật lan truyền độ không đảm bảo (xem Điều 5) theo cách gọi của tiêu chuẩn này.
3.3.7. Để đáp ứng các nhu cầu áp dụng của một số ngành công nghiệp và thương mại, cũng như các yêu cầu trong lĩnh vực y tế và an toàn, độ không đảm bảo mở rộng U nhận được bằng cách nhân độ không đảm bảo chuẩn tổng hợp uc với hệ số phủ k. Mục đích dự kiến của U là cung cấp khoảng quanh kết quả đo mà có thể được kỳ vọng chứa phần lớn phân bố các giá trị có thể quy cho đại lượng đo một cách hợp lý. Việc lựa chọn hệ số k, thường từ 2 đến 3, dựa trên xác suất phủ hoặc mức tin cậy yêu cầu của khoảng (xem Điều 6).
CHÚ THÍCH: Hệ số phủ k luôn được công bố, do đó độ không đảm bảo chuẩn của đại lượng đo được có thể được khôi phục lại để sử dụng trong tính toán độ không đảm bảo chuẩn tổng hợp của các kết quả đo khác có thể phụ thuộc vào đại lượng đo.
3.4. Xem xét thực tế
3.4.1. Nếu tất cả các đại lượng mà kết quả đo phụ thuộc vào chúng thay đổi thì độ không đảm bảo có thể được đánh giá bằng công cụ thống kê. Tuy nhiên, vì điều này ít có trong thực tế do hạn chế về thời gian và nguồn lực nên độ không đảm bảo của kết quả đo thường được đánh giá bằng cách sử dụng mô hình toán của phép đo và định luật lan truyền độ không đảm bảo. Do đó, trong tiêu chuẩn này giả định rằng phép đo có thể được lập mô hình toán tới mức độ chính xác yêu cầu của phép đo.
3.4.2. Vì mô hình toán có thể không hoàn chỉnh nên tất cả các đại lượng liên quan cần được thay đổi tới mức có thể thực hiện đầy đủ nhất để việc đánh giá độ không đảm bảo có thể được dựa trên dữ liệu quan trắc được càng nhiều càng tốt. Bất cứ khi nào có thể, việc sử dụng các mô hình thực nghiệm của phép đo được dựa trên dữ liệu định lượng dài hạn và việc sử dụng các chuẩn kiểm tra và biểu đồ kiểm soát có thể chỉ ra việc phép đo có nằm trong trạng thái kiểm soát thống kê hay không, cần là một phần của nỗ lực để có được sự đánh giá tin cậy về độ không đảm bảo. Mô hình toán cần luôn được xem xét sửa đổi khi dữ liệu quan trắc được, bao gồm cả kết quả của các phép xác định độc lập cùng đại lượng, chứng tỏ rằng mô hình trên là không hoàn chỉnh. Thực nghiệm được tổ chức tốt có thể tạo thuận lợi cho các đánh giá đáng tin cậy về độ không đảm bảo và là một phần quan trọng của nghệ thuật đo lường.
3.4.3. Để quyết định việc hệ thống đo có hoạt động chính xác hay không thì biến động quan trắc thực nghiệm của các giá trị đầu ra của nó, được đo bằng độ lệch chuẩn quan trắc được, thường được so sánh với độ lệch chuẩn dự đoán nhận được bằng cách kết hợp các thành phần độ không đảm bảo khác nhau đặc trưng cho phép đo. Trong trường hợp như vậy, chỉ các thành phần (nhận được từ đánh giá Loại A và Loại B) có thể đóng góp vào biến động quan trắc thực nghiệm của các giá trị đầu ra này mới cần được xem xét.
CHÚ THÍCH: Phân tích như vậy có thể được tạo thuận lợi bằng cách tập hợp các thành phần đóng góp vào độ biến động và không ở trong hai nhóm ghi riêng biệt và thích hợp.
3.4.4. Trong một số trường hợp, độ không đảm bảo của sự hiệu chính đối với ảnh hưởng hệ thống không cần được tính đến trong việc đánh giá độ không đảm bảo của kết quả đo. Mặc dù độ không đảm bảo đã được đánh giá nhưng có thể bỏ qua nếu đóng góp của nó vào độ không đảm bảo chuẩn tổng hợp của kết quả đo là không đáng kể. Nếu bản thân giá trị hiệu chính là không đáng kể so với độ không đảm bảo chuẩn tổng hợp thì cũng có thể bỏ qua.
3.4.5. Trong thực tế thường xảy ra, đặc biệt là trong lĩnh vực đo lường pháp định, thiết bị được thử nghiệm thông qua việc so sánh với chuẩn đo lường và độ không đảm bảo gắn với chuẩn và thủ tục so sánh không đáng kể so với độ chính xác yêu cầu của phép thử. Ví dụ như sử dụng một tập hợp các chuẩn khối lượng đã được hiệu chuẩn tốt để thử nghiệm độ chính xác của cân thương mại. Trong trường hợp như vậy, do các thành phần của độ không đảm bảo là đủ nhỏ để bỏ qua nên phép đo có thể được coi là xác định sai số của thiết bị được thử nghiệm. (Xem thêm F.2.4.2)
3.4.6. Ước lượng giá trị của đại lượng đo từ kết quả đo đôi khi được trình bày theo giá trị được thừa nhận của chuẩn đo lường hơn là theo đơn vị liên quan của Hệ đơn vị quốc tế (SI). Trong trường hợp đó, độ lớn của độ không đảm bảo có thể gán cho kết quả đo có thể nhỏ hơn nhiều so với khi kết quả đó được trình bày theo đơn vị SI liên quan. (Trong thực tế, đại lượng đo đã được xác định lại là tỷ số giá trị của đại lượng được đo trên giá trị được thừa nhận của chuẩn).
VÍ DỤ: Chuẩn điện áp Zener chất lượng cao được hiệu chuẩn bằng cách so sánh với quy chiếu điện áp hiệu ứng Josephson trên cơ sở giá trị quy ước của hằng số Josephson được CIPM khuyến nghị sử dụng quốc tế. Độ không đảm bảo của chuẩn kết hợp tương đối uc(Vs)/Vs (xem 5.1.6) của hiệu điện thế được hiệu chuẩn Vs của chuẩn Zener bằng 2 x 10-8 khi Vs được báo cáo dưới dạng giá trị quy ước, nhưng uc(Vs)/Vs bằng 4 x 10-7 khi Vs được báo cáo dưới dạng đơn vị SI hiệu điện thế, vôn (V), do độ không đảm bảo bổ sung gắn với giá trị SI của hằng số Josephson.
3.4.7. Sai lầm khi báo cáo hoặc phân tích dữ liệu có thể tạo ra sai số chưa biết lớn trong kết quả đo. Sai lầm lớn thường có thể được xác định bằng việc xem xét thích hợp dữ liệu, sai lầm nhỏ có thể bị che đậy bởi, hoặc thậm chí xuất hiện như, độ biến động ngẫu nhiên. Việc đo độ không đảm bảo không dự định tính đến các sai lầm như vậy.
3.4.8. Mặc dù tiêu chuẩn này cung cấp khuôn khổ để đánh giá độ không đảm bảo nhưng không thể thay thế cho các tư duy phê phán, sự trung thực và kỹ năng chuyên môn. Việc đánh giá độ không đảm bảo không phải là nhiệm vụ thường xuyên và cũng không phải là toán học thuần túy; nó phụ thuộc vào hiểu biết chi tiết về tính chất của đại lượng đo và phép đo. Do đó, chất lượng và tính khả dụng của độ không đảm bảo trích dẫn cho kết quả đo phụ thuộc chủ yếu vào sự hiểu biết, phân tích điểm trọng yếu và tính trung thực của những người tham gia vào việc ấn định giá trị của nó.
4. Đánh giá độ không đảm bảo chuẩn
Hướng dẫn bổ sung về đánh giá các thành phần độ không đảm bảo, chủ yếu là dạng thực hành, có thể tìm thấy trong Phụ lục F.
4.1 Lập mô hình phép đo
4.1.1. Trong hầu hết các trường hợp, đại lượng đo Y không được phép đo trực tiếp mà được xác định từ N đại lượng khác X1, X2, … , XN thông qua mối quan hệ hàm f:
Y = f(X1,X2,…,XN) (1)
CHÚ THÍCH 1: Để thống nhất về ký hiệu, tiêu chuẩn này sử dụng cùng một ký hiệu cho đại lượng vật lý (đại lượng đo) và cho biến ngẫu nhiên (xem 4.2.1) miêu tả kết quả có thể có của quan trắc đại lượng đo. Khi ấn định Xi có phân bố xác suất cụ thể thì ký hiệu đó được sử dụng theo ý nghĩa đề cập sau; giả định rằng bản thân đại lượng vật lý có thể được đặc trưng bằng giá trị cơ bản duy nhất (xem 1.2 và 3.1.3).
CHÚ THÍCH 2: Trong dãy các quan trắc, giá trị quan trắc được thứ k của Xi được ký hiệu là Xi,k; do đó nếu R biểu thị giá trị điện trở của một điện trở, thì giá trị quan trắc được thứ k của điện trở được ký hiệu là Rk.
CHÚ THÍCH 3: Ước lượng của Xi (nói đúng ra là kỳ vọng của nó) được ký hiệu là xi.
Ví dụ: Nếu hiệu điện thế V được đặt vào các cực của điện trở phụ thuộc nhiệt độ có điện trở Ro ở nhiệt độ đã biết to và hệ số nhiệt độ tuyến tính của điện trở α, thì công suất P (đại lượng đo) bị tiêu hao do điện trở ở nhiệt độ t phụ thuộc vào V, Ro, α, và t theo:
P = f(V,Ro,α,t) = V2/{Ro[1 + α(t-t0)]}
CHÚ THÍCH: Các phương pháp đo P khác được lập mô hình bằng các biểu thức toán khác nhau.
4.1.2. Các đại lượng đầu vào X1, X2, … , XN mà đại lượng đầu ra Y phụ thuộc có thể được coi là đại lượng đo và có thể phụ thuộc vào các đại lượng khác, bao gồm sự hiệu chính và các thừa số hiệu chỉnh đối với ảnh hưởng hệ thống, từ đó dẫn tới mối quan hệ hàm số phức tạp f có thể không bao giờ viết được ra rõ ràng. Hơn nữa, f có thể được xác định bằng thực nghiệm (xem 5.1.4) hoặc chỉ tồn tại như một thuật toán phải được đánh giá bằng số. Hàm số f xuất hiện trong tiêu chuẩn này được hiểu theo ngữ cảnh rộng hơn này, đặc biệt khi hàm số đó chứa mọi đại lượng, bao gồm tất cả các số hiệu chính và thừa số hiệu chính có thể đóng góp một thành phần độ không đảm bảo quan trọng vào kết quả đo.
Do đó, nếu dữ liệu chỉ ra rằng f không lập mô hình phép đo tới độ chính xác yêu cầu của kết quả đo thì các đại lượng đầu vào bổ sung phải được bao gồm trong f để loại trừ sự không thỏa đáng (xem 3.4.2). Điều này có thể yêu cầu đưa ra một đại lượng đầu vào để phản ánh sự hiểu biết không đầy đủ về hiện tượng tác động tới đại lượng đo. Trong ví dụ của 4.1.1, các đại lượng đầu vào bổ sung có thể cần thiết để giải thích cho phân bố nhiệt độ không đều để biết qua điện trở, hệ số nhiệt độ phi tuyến có thể có của điện trở hoặc sự phụ thuộc có thể có của điện trở vào áp suất khí quyển.
CHÚ THÍCH: Tuy nhiên, phương trình (1) có thể đơn giản là Y = X1 – X2. Ví dụ, cách trình bày này lập mô hình so sánh hai phép xác định của cùng đại lượng X.
4.1.3. Tập hợp các đại lượng đầu vào X1, X2, …, XN có thể được phân loại thành:
– các đại lượng có giá trị và độ không đảm bảo được xác định trực tiếp trong phép đo hiện tại. Các giá trị và độ không đảm bảo này có thể nhận được từ, ví dụ, quan trắc đơn, các quan trắc lặp lại hoặc suy luận dựa trên kinh nghiệm và có thể bao gồm xác định sự hiệu chính số đọc của phương tiện đo và sự hiệu chỉnh đối với các đại lượng ảnh hưởng, như nhiệt độ môi trường, áp suất không khí và độ ẩm;
– các đại lượng có giá trị và độ không đảm bảo được đưa vào phép đo từ các nguồn bên ngoài, như các đại lượng gắn với chuẩn đo lường đã được hiệu chuẩn, mẫu chuẩn được chứng nhận và dữ liệu tra cứu từ sổ tay.
4.1.4. Ước lượng đại lượng đo Y, ký hiệu là y, nhận được từ Phương trình (1) bằng cách sử dụng các ước lượng đầu vào x1, x2, …, xN đối với giá trị của N đại lượng X1, X2, …, XN. Do đó, ước lượng đầu ra y, là kết quả đo, được cho bởi:
y = f(x=, x2, …, xN) (2)
CHÚ THÍCH: Trong một số trường hợp, ước lượng y có thể nhận được từ:
![]()
Trong đó, y được lấy như trung bình cộng hoặc giá trị trung bình (xem 4.2.1) của n phép xác định độc lập Yk của Y, mỗi phép xác định có cùng độ không đảm bảo và được dựa trên một tập hợp đầy đủ các giá trị quan trắc được của N đại lượng đầu vào Xi nhận được đồng thời. Cách tính trung bình này tốt hơn ![]() , trong đó
, trong đó
![]()
là trung bình cộng của các quan trắc độc lập Xi,k, có thể thích hợp hơn khi f là hàm phi tuyến của các đại lượng đầu vào X1, X2,…, XN, nhưng hai cách tiếp cận là như nhau nếu f là hàm tuyến tính của Xi (xem H.2 và H.4).
4.1.5. Độ lệch chuẩn ước lượng gắn với ước lượng đầu ra hoặc kết quả đo y, được gọi là không đảm bảo chuẩn tổng hợp và ký hiệu là uc(y), được xác định từ độ lệch chuẩn ước lượng gắn với từng ước lượng đầu vào xi, được gọi là độ lệch chuẩn và ký hiệu là u(xi) (xem 3.3.5 và 3.3.6).
4.1.6. Mỗi ước lượng đầu vào xi và độ lệch chuẩn gắn với nó u(xi) nhận được từ phân bố các giá trị có thể có của đại lượng đầu vào Xi. Phân bố xác suất này có thể là tần suất được dựa trên một dãy các quan trắc Xi,k của Xi hoặc có thể là một phân bố tiên nghiệm. Đánh giá Loại A của các thành phần độ không đảm bảo chuẩn được tìm thấy ở phân bố tần suất trong khi đánh giá Loại B được tìm thấy ở phân bố tiên nghiệm. Phải thừa nhận rằng trong cả hai trường hợp các phân bố là các mô hình được sử dụng để đại diện cho trình độ hiểu biết của chúng ta.
4.2. Đánh giá độ không đảm bảo chuẩn loại A
4.2.1. Trong hầu hết các trường hợp, ước lượng có sẵn tốt nhất của kỳ vọng hoặc giá trị được kỳ vọng mq của đại lượng q thay đổi ngẫu nhiên [biến ngẫu nhiên (C.2.2)] và đối với n quan trắc độc lập qk đã nhận được ở cùng điều kiện đo (xem B.2.15) là trung bình cộng hoặc trung bình ![]() (C.2.19) của n quan trắc:
(C.2.19) của n quan trắc:
![]() (3)
(3)
Do đó, đối với đại lượng đầu vào Xi được ước lượng từ n quan trắc lặp lại độc lập Xi,k, trung bình cộng ![]() nhận được từ biểu thức (3) được sử dụng như là ước lượng đầu vào xi trong biểu thức (2) để xác định kết quả đo y; đó là: xi =
nhận được từ biểu thức (3) được sử dụng như là ước lượng đầu vào xi trong biểu thức (2) để xác định kết quả đo y; đó là: xi = ![]() . Các ước lượng đầu vào không được đánh giá từ các quan trắc lặp lại đó phải nhận được từ các phương pháp khác, như được trình bày trong nhóm thứ hai của 4.1.3.
. Các ước lượng đầu vào không được đánh giá từ các quan trắc lặp lại đó phải nhận được từ các phương pháp khác, như được trình bày trong nhóm thứ hai của 4.1.3.
4.2.2. Các quan trắc độc lập qk khác nhau về giá trị do biến động ngẫu nhiên trong đại lượng ảnh hưởng hoặc do các ảnh hưởng ngẫu nhiên (xem 3.2.2). Phương sai thực nghiệm của các quan trắc, ước lượng phương sai s2 của phân bố xác xuất của q, được cho bằng:
![]() (4)
(4)
Ước lượng này của phương sai và dương căn bậc hai s(qk), được gọi là độ lệch chuẩn thực nghiệm (B.2.17), đặc trưng cho độ biến động các giá trị quan trắc qk, cụ thể hơn là sự phân tán của chúng quanh trung bình ![]() .
.
4.2.3. Ước lượng tốt nhất của s2(![]() ) = s2/n, phương sai của trung bình, được cho bởi:
) = s2/n, phương sai của trung bình, được cho bởi:
![]() (5)
(5)
Phương sai thực nghiệm của trung bình ![]() và độ lệch chuẩn thực nghiệm của trung bình
và độ lệch chuẩn thực nghiệm của trung bình ![]() (B.2.17, Chú thích 2) bằng dương căn bậc hai của
(B.2.17, Chú thích 2) bằng dương căn bậc hai của ![]() , định lượng
, định lượng ![]() ước lượng kỳ vọng mq của q và có thể được sử dụng như thước đo độ không đảm bảo của
ước lượng kỳ vọng mq của q và có thể được sử dụng như thước đo độ không đảm bảo của ![]() .
.
Do đó, đối với đại lượng đầu vào Xi được xác định từ n quan trắc lặp lại độc lập Xi,k, độ không đảm bảo chuẩn u(xi) của ước lượng xi = ![]() , là (u(xi) = s(
, là (u(xi) = s(![]() ), với s2(
), với s2(![]() ) được tính theo phương trình (5). Để thuận tiện, u2(xi) = s2(
) được tính theo phương trình (5). Để thuận tiện, u2(xi) = s2(![]() ) và u(xi) = s(
) và u(xi) = s(![]() ) đôi khi được gọi là phương sai Loại A và độ không đảm bảo chuẩn Loại A, tương ứng.
) đôi khi được gọi là phương sai Loại A và độ không đảm bảo chuẩn Loại A, tương ứng.
CHÚ THÍCH 1: Số các quan trắc n cần đủ lớn để đảm bảo rằng ![]() đưa ra ước lượng đáng tin cậy cho kỳ vọng mq của biến ngẫu nhiên q và s2(
đưa ra ước lượng đáng tin cậy cho kỳ vọng mq của biến ngẫu nhiên q và s2(![]() ) đưa ra ước lượng tin cậy của phương sai s2(
) đưa ra ước lượng tin cậy của phương sai s2(![]() ) = s2/n (xem 4.3.2, chú thích). Sự khác nhau giữa s2(
) = s2/n (xem 4.3.2, chú thích). Sự khác nhau giữa s2(![]() ) và s2(
) và s2(![]() ) phải được xem xét khi xây dựng khoảng tin cậy (xem 6.2.2). Trong trường hợp này, nếu phân bố xác suất của q là phân bố chuẩn (xem 4.3.4) thì sự khác nhau được tính đến thông qua phân bố t (xem G.3.2).
) phải được xem xét khi xây dựng khoảng tin cậy (xem 6.2.2). Trong trường hợp này, nếu phân bố xác suất của q là phân bố chuẩn (xem 4.3.4) thì sự khác nhau được tính đến thông qua phân bố t (xem G.3.2).
CHÚ THÍCH 2: Mặc dù phương sai s2(![]() ) là đại lượng cơ bản hơn nhưng trong thực tế độ lệch chuẩn s(
) là đại lượng cơ bản hơn nhưng trong thực tế độ lệch chuẩn s(![]() ) lại thuận tiện hơn vì cùng thứ nguyên với q và có giá trị dễ hiểu hơn so với phương sai.
) lại thuận tiện hơn vì cùng thứ nguyên với q và có giá trị dễ hiểu hơn so với phương sai.
4.2.4. Đối với phép đo được đặc trưng tốt trong trạng thái kiểm soát thống kê, có thể có sẵn ước lượng kết hợp hoặc gộp của phương sai ![]() (hoặc độ lệch chuẩn thực nghiệm gộp sp) đặc trưng cho phép đo. Trong trường hợp đó, khi giá trị của đại lượng đo q được xác định từ n quan trắc độc lập thì phương sai thực nghiệm của trung bình cộng
(hoặc độ lệch chuẩn thực nghiệm gộp sp) đặc trưng cho phép đo. Trong trường hợp đó, khi giá trị của đại lượng đo q được xác định từ n quan trắc độc lập thì phương sai thực nghiệm của trung bình cộng ![]() của các quan trắc được ước lượng bằng
của các quan trắc được ước lượng bằng ![]() /n tốt hơn so với bằng s2(pk)/n và độ không đảm bảo chuẩn là
/n tốt hơn so với bằng s2(pk)/n và độ không đảm bảo chuẩn là ![]() (Xem thêm Chú thích của H.3.6).
(Xem thêm Chú thích của H.3.6).
4.2.5. Ước lượng xi của đại lượng đầu vào Xi thường nhận được từ đường cong đã được làm khớp với dữ liệu thực nghiệm bằng phương pháp bình phương tối thiểu. Phương sai ước lượng và độ không đảm bảo chuẩn nhận được của các tham số được làm khớp đặc trưng cho đường cong của các điểm dự đoán thường có thể được tính bằng các thủ tục thống kê phủ biến (xem H.3 và Tài liệu tham khảo [8]).
4.2.6. Bậc tự do (C.2.31) vi của u(xi) (xem G.3), bằng n-1 trong trường hợp đơn giản khi xi = ![]() và u(xi) = s(
và u(xi) = s(![]() ) được tính từ n quan trắc độc lập như trong 4.2.1 và 4.2.3, luôn cần được cho trước khi lập tài liệu đánh giá thành phần độ không đảm bảo Loại A.
) được tính từ n quan trắc độc lập như trong 4.2.1 và 4.2.3, luôn cần được cho trước khi lập tài liệu đánh giá thành phần độ không đảm bảo Loại A.
4.2.7. Nếu độ biến động ngẫu nhiên trong quan trắc đại lượng đầu vào có tương quan, ví dụ, theo thời gian, thì trung bình và độ lệch chuẩn thực nghiệm của trung bình như trong 4.2.1 và 4.2.3 có thể là các hàm ước lượng (C.2.25) không thích hợp của thống kê học (C.2.23) được yêu cầu. Trong trường hợp đó, các quan trắc cần được phân tích bằng các phương pháp thống kê được thiết kế riêng để xử lý dãy các phép đo tương quan, thay đổi ngẫu nhiên.
CHÚ THÍCH: Các phương pháp chuyên dùng như vậy được sử dụng để xử lý các phép đo chuẩn tần số. Tuy nhiên, có thể từ phép đo ngắn hạn tới phép đo dài hạn của các đại lượng đo lường khác, việc giả định các biến động ngẫu nhiên không tương quan có thể không còn giá trị và các phương pháp chuyên dùng cũng có thể được sử dụng để xử lý các phép đo này (Ví dụ, xem ở Tài liệu tham khảo [9], thảo luận chi tiết về phương pháp Allan).
4.2.8. Thảo luận về đánh giá độ không đảm bảo chuẩn Loại A trong các Điều từ 4.2.1 tới 4.2.7 chưa phải là đầy đủ; có nhiều tình huống, một số tương đối phức tạp, có thể được xử lý bằng các phương pháp thống kê. Ví dụ quan trọng là việc sử dụng thiết kế hiệu chuẩn, thường dựa trên phương pháp bình phương tối thiểu, để đánh giá độ không đảm bảo xuất hiện từ biến động ngẫu nhiên ngắn hạn và dài hạn trong kết quả so sánh của các vật mẫu vật liệu chưa biết giá trị, như bộ can mẫu và chuẩn khối lượng, với chuẩn chính đã biết giá trị. Trong tình huống phép đo tương đối đơn giản như vậy, các thành phần độ không đảm bảo thường có thể được đánh giá bằng phân tích thống kê dữ liệu nhận được từ các thiết kế gồm dãy ghép đo các đại lượng đo đối với một số giá trị khác nhau của các đại lượng nó phụ thuộc – được gọi là phân tích phương sai (xem H.5).
CHÚ THÍCH: Ở cấp độ thấp hơn của chuỗi hiệu chuẩn, khi các chuẩn chính thường được giả định là biết chính xác vì chúng đã được hiệu chuẩn bởi các phòng thí nghiệm chuẩn quốc gia và chuẩn đầu, thì độ không đảm bảo của kết quả hiệu chuẩn có thể là độ không đảm bảo chuẩn Loại A đơn được đánh giá từ độ lệch chuẩn thực nghiệm gộp đặc trưng cho phép đo.
4.3. Đánh giá độ không đảm bảo chuẩn loại B
4.3.1. Đối với ước lượng xi của đại lượng đầu vào Xi không nhận được từ các quan trắc lặp lại thì phương sai ước lượng kèm theo u2(xi) hoặc độ không đảm bảo chuẩn u(xi) được đánh giá bằng sự nhận định khoa học dựa trên tất cả thông tin có sẵn về độ biến động có thể có của Xi. Tổ hợp thông tin có thể bao gồm:
– dữ liệu đo trước đó;
– kinh nghiệm hoặc sự hiểu biết chung về trạng thái hoặc tính chất của vật liệu và phương tiện liên quan;
– quy định kỹ thuật của nhà sản xuất;
– dữ liệu được cung cấp trong giấy chứng nhận hiệu chuẩn và các giấy chứng nhận khác;
– độ không đảm bảo được ấn định cho dữ liệu tra cứu từ sổ tay.
Để thuận tiện, u2(xi) và u(xi) được đánh giá theo cách này đôi khi được gọi tương ứng là phương sai Loại B và độ lệch chuẩn Loại B.
CHÚ THÍCH: Khi xi nhận được từ phân bố tiên nhiệm, phương sai kèm theo được viết thích hợp là u2(Xi) nhưng để đơn giản, u2(xi) và u(xi) được sử dụng trong toàn bộ tiêu chuẩn này.
4.3.2. Việc sử dụng đúng tổ hợp thông tin có sẵn đối với việc đánh giá độ không đảm bảo chuẩn Loại B đòi hỏi cái nhìn sâu sắc dựa trên kinh nghiệm và sự hiểu biết chung và là kỹ năng có thể học cùng với thực hành. Cần thừa nhận rằng đánh giá độ không đảm bảo chuẩn Loại B đáng tin cậy như đánh giá Loại A, đặc biệt là trong trường hợp phép đo mà đánh giá Loại A được dựa trên cơ sở số lượng tương đối ít các quan trắc độc lập thống kê.
CHÚ THÍCH: Nếu phân bố xác suất của q trong Chú thích 1 của 4.2.3 là chuẩn thì s[d(![]() )/s(
)/s(![]() )], độ lệch chuẩn của s(
)], độ lệch chuẩn của s(![]() ) so với s(
) so với s(![]() ), xấp xỉ bằng [2(n-1)]-1/2. Do đó, xem s[s(
), xấp xỉ bằng [2(n-1)]-1/2. Do đó, xem s[s(![]() )] là độ không đảm bảo của s(
)] là độ không đảm bảo của s(![]() ), đối với n = 10 quan trắc, độ không đảm bảo tương đối của s(
), đối với n = 10 quan trắc, độ không đảm bảo tương đối của s(![]() ) là 24%, trong khi với n = 50 quan trắc là 10%. (Các giá trị bổ sung được nêu trong Bảng E.1, Phụ lục E).
) là 24%, trong khi với n = 50 quan trắc là 10%. (Các giá trị bổ sung được nêu trong Bảng E.1, Phụ lục E).
4.3.3. Nếu ước lượng xi được lấy từ quy định kỹ thuật của nhà sản xuất, giấy chứng nhận hiệu chuẩn, sổ tay hoặc nguồn khác và độ không đảm bảo trích dẫn được quy định là bội cụ thể của độ lệch chuẩn thì độ không đảm bảo chuẩn u(xi) đơn giản bằng giá trị trích dẫn chia cho số nhân và phương sai ước lượng u2(xi) là bình phương của thương đó.
VÍ DỤ: Giấy chứng nhận hiệu chuẩn quy định rằng khối lượng của chuẩn khối lượng của thép không gỉ ms của giá trị danh nghĩa một kilogam là 1 000,000 325 g và “độ không đảm bảo của giá trị này là 240 mg ở độ lệch chuẩn ba”. Khi đó độ không đảm bảo chuẩn của chuẩn khối lượng đơn giản bằng u(ms) = (240 mg)/3 = 80mg. Điều này phù hợp với độ không đảm bảo chuẩn tương đối u(ms)/ms bằng 80 x 10-9 (xem 5.1.6). Phương sai ước lượng bằng u2(ms) = (80 mg)2 = 6,4 x 10-9 g2.
CHÚ THÍCH: Trong nhiều trường hợp, có ít hoặc không có thông tin được cung cấp về các thành phần riêng biệt từ đó nhận được độ không đảm bảo trích dẫn. Điều này thường không quan trọng đối với trình bày độ không đảm bảo theo thực tiễn của tiêu chuẩn này vì tất cả các độ không đảm bảo chuẩn được xử lý theo cùng một cách khi tính toán độ không đảm bảo chuẩn tổng hợp của kết quả đo (xem Điều 5).
4.3.4. Độ không đảm bảo trích dẫn của xi không nhất thiết được cho là bội số của độ lệch chuẩn như trong 4.3.3. Thay vào đó, có thể tìm thấy công bố rằng độ không đảm bảo trích dẫn định nghĩa khoảng có mức tin cậy 90%, 95% hoặc 99% (xem 6.2.2). Trừ khi được chỉ định khác, có thể giả định rằng phân bố chuẩn (C.2.14) đã được sử dụng để tính độ không đảm bảo trích dẫn và tìm lại độ không đảm bảo chuẩn của xi bằng cách chia độ không đảm bảo trích dẫn cho hệ số thích hợp của phân bố chuẩn. Hệ số tương ứng với ba mức tin cậy ở trên là 1,64; 1,96 và 2,58 (xem thêm Bảng G.1 Phụ lục G).
CHÚ THÍCH: Không cần phải giả định như vậy nếu độ không đảm bảo được cho phù hợp với khuyến nghị của tiêu chuẩn này liên quan tới báo cáo độ không đảm bảo, trong đó nhấn mạnh rằng hệ số phủ sử dụng luôn được cho trước (xem 7.2.3).
VÍ DỤ: Giấy chứng nhận hiệu chuẩn thông báo rằng điện trở của điện trở chuẩn Rs của giá trị danh nghĩa mười ôm là 10,000 742 W ± 129 mW ở 230C và “độ không đảm bảo trích dẫn 129 mW xác định khoảng có mức tin cậy 99%”. Độ không đảm bảo chuẩn của điện trở có thể lấy là u(Rs) = (129 mW/2,58 = 50 mW), tương ứng với độ không đảm bảo chuẩn tương đối u(Rs)/Rs là 5,0 x 10-6 (xem 5.1.6). Phương sai ước lượng là u2(Rs) = (50mW)2 = 2,5 x 10-9 W2
4.3.5. Xét trường hợp, dựa trên thông tin có sẵn, có thể quy định rằng “có năm mươi – năm mươi cơ hội giá trị đại lượng đầu vào Xi nằm trong khoảng a– đến a+” (nói cách khác, xác suất Xi nằm trong khoảng này là 0,5% hoặc 50%). Nếu có thể giả định rằng phân bố của giá trị Xi có thể có là xấp xỉ chuẩn thì ước lượng tốt nhất xi của Xi có thể được lấy là điểm giữa của khoảng. Ngoài ra, nếu một nửa độ rộng của khoảng được ký hiệu là a = a+ – a–)/2 thì có thể lấy u(xi) = 1,48a, vì đối với phân bố chuẩn với kỳ vọng m và độ lệch chuẩn s thì khoảng m±s/1,48 chứa khoảng 50% phân bố.
VÍ DỤ: Một thợ máy xác định kích thước của một bộ phận ước tính rằng, với xác suất 0,5, độ dài của nó nằm trong khoảng 10,07 mm đến 10,15 mm và báo cáo rằng l = (10,11 ± 0,04) mm, nghĩa là ±0,04 mm xác định khoảng có mức tin cậy 50%. Do đó a = 0,04 mm, và nếu giả định phân bố chuẩn cho giá trị có thể của l thì độ không đảm bảo chuẩn của độ dài là u(l) = 1,48 x 0,04 mm » 0,06 mm và phương sai ước lượng là u2(l) = (1,48 x 0,04 mm)2 = 3,5 x 10-3 mm2.
4.3.6. Xét trường hợp tương tự như 4.3.5 nhưng, dựa trên thông tin có sẵn, có thể nói rằng “có khoảng hai trong số ba cơ hội giá trị Xi nằm trong khoảng a– đến a+” (nói cách khác, xác xuất Xi nằm trong khoảng này là khoảng 0,67). Khi đó có thể lấy hợp lý u(xi) = a, vì đối với phân bố chuẩn với kỳ vọng m và độ lệch chuẩn s thì khoảng m±s chứa khoảng 68,3% phân bố.
CHÚ THÍCH: Sẽ có giá trị u(xi) lớn hơn đáng kể so với được bảo đảm rõ ràng nếu sử dụng độ lệch chuẩn thực tế 0,967 42 tương ứng với xác suất p = 2/3, nghĩa là, nếu nó được viết là u(xi) = a/0,967 42 = 1,033a.
4.3.7. Trong trường hợp khác, có thể có khả năng chỉ ước lượng phạm vi (giới hạn trên và dưới) cho Xi, cụ thể, quy định rằng “xác suất để giá trị Xi nằm trong khoảng a– đến a+ đối với tất cả các mục đích thực tiễn là bằng một và xác suất Xi nằm ngoài khoảng này về cơ bản là bằng “không”. Nếu không có hiểu biết cụ thể về giá trị có thể có của Xi trong khoảng thì chỉ có thể giả định rằng xác suất để Xi nằm bất kỳ đâu trong khoảng đó là như nhau (phân bố đều hoặc hình chữ nhật của các giá trị có thể có – xem 4.4.5 và Hình 2a). Khi đó xi, kỳ vọng hoặc giá trị kỳ vọng của Xi, là điểm giữa của khoảng, xi = (a– + a+)/2, với phương sai đi kèm:
u2(xi) = (a+ – a–)2/12 (6)
Nếu hiệu giữa các biên, a+ – a-_, được ký hiệu là 2a thì phương trình (6) trở thành:
u2(xi) = a2/3 (7)
CHÚ THÍCH: Thành phần của độ không đảm bảo được xác định theo cách này đóng phần đáng kể vào độ không đảm bảo của kết quả đo, nên thận trọng thu thập dữ liệu bổ sung cho việc đánh giá tiếp theo.
VÍ DỤ 1: Sổ tay cung cấp giá trị hệ số giãn nở dài do nhiệt của đồng nguyên chất ở 200C, α20(Cu), là 16,52 x 10-6 0C-1 và nêu đơn giản rằng “sai số trong giá trị này không được vượt quá 0,40 x 10-6 0C-1“. Dựa trên thông tin hạn chế này, sẽ không hợp lý khi giả định rằng giá trị của α20(Cu) có xác suất như nhau nằm trong khoảng 16,12 x 10-6 0C-1 đến 16,92 x 10-6 0C-1 và rất không chắc chắn là α20(Cu) nằm ngoài khoảng này. Phương sai của phân bố chữ nhật đối xứng này của giá trị α20(Cu) có thể có với một nửa độ rộng a = 0,40 x 10-6 0C-1 theo Phương trình (7), sẽ bằng u2(α20) = (0,40 x 10-6 0C-1)2/3 = 53,3×10-15 0C-2 và độ không đảm bảo chuẩn là u(α20) = (0,40 x 10-6 0C-1)/![]() = 0,23 x 10-6 0C-1.
= 0,23 x 10-6 0C-1.
VÍ DỤ 2: Quy định kỹ thuật của nhà sản xuất đối với vôn kế hiện số nêu rõ “từ một đến hai năm sau khi phương tiện đo được hiệu chuẩn, độ chính xác trong thang độ rộng 1 V là 14×10-6 lần giá trị đọc cộng 2 x 10-6 lần độ rộng”. Coi phương tiện được sử dụng 20 tháng sau khi hiệu chuẩn để đo hiệu điện thế V trên độ rộng 1V và trung bình cộng của số quan trắc lặp lại độc lập của V tìm được là ![]() = 0,928 571 V với độ không đảm bảo chuẩn Loại A u(
= 0,928 571 V với độ không đảm bảo chuẩn Loại A u(![]() ) = 12 mV. Có thể thu được độ không đảm bảo chuẩn gắn với quy định kỹ thuật của nhà sản xuất về độ không đảm bảo từ đánh giá Loại B bằng cách giả định rằng độ chính xác quy định cung cấp biên đối xứng cho sự hiệu chính bổ sung đối với
) = 12 mV. Có thể thu được độ không đảm bảo chuẩn gắn với quy định kỹ thuật của nhà sản xuất về độ không đảm bảo từ đánh giá Loại B bằng cách giả định rằng độ chính xác quy định cung cấp biên đối xứng cho sự hiệu chính bổ sung đối với ![]() ,
, ![]() , của kỳ vọng bằng “không” và nằm ở bất kỳ đâu trong biên này với xác suất ngang nhau. Một nửa độ rộng của phân bố chữ nhật đối xứng các giá trị có thể có của
, của kỳ vọng bằng “không” và nằm ở bất kỳ đâu trong biên này với xác suất ngang nhau. Một nửa độ rộng của phân bố chữ nhật đối xứng các giá trị có thể có của ![]() là a = (14 x 10-6) x (0,928 571 V) + (2 x 10-6) x (1V) = 15 mV, và từ phương trình (7), u2(
là a = (14 x 10-6) x (0,928 571 V) + (2 x 10-6) x (1V) = 15 mV, và từ phương trình (7), u2(![]() ) = 75 mV2 và u2(
) = 75 mV2 và u2(![]() ) = 8,7 mV. Ước lượng giá trị của đại lượng đo V, để đơn giản cũng được ký hiệu là V, được cho bằng V =
) = 8,7 mV. Ước lượng giá trị của đại lượng đo V, để đơn giản cũng được ký hiệu là V, được cho bằng V = ![]() +
+![]() = 0,928 571 V . Có thể thu được độ không đảm bảo chuẩn tổng hợp của ước lượng này bằng cách kết hợp 12mV độ không đảm bảo chuẩn Loại A của V với 8,7 mV độ không đảm bảo chuẩn Loại B của
= 0,928 571 V . Có thể thu được độ không đảm bảo chuẩn tổng hợp của ước lượng này bằng cách kết hợp 12mV độ không đảm bảo chuẩn Loại A của V với 8,7 mV độ không đảm bảo chuẩn Loại B của![]() . Phương pháp chung để tổng hợp các thành phần của độ không đảm bảo chuẩn được cho trong Điều 5, ví dụ cụ thể được cho trong 5.1.5.
. Phương pháp chung để tổng hợp các thành phần của độ không đảm bảo chuẩn được cho trong Điều 5, ví dụ cụ thể được cho trong 5.1.5.
4.3.8. Trong 4.3.7, biên trên và dưới a+ và a– đối với đại lượng đầu vào Xi có thể không đối xứng về ước lượng tốt nhất xi; cụ thể hơn, nếu biên dưới được viết là a– = xi – b– và biên trên là a+ = xi – b+ thì b– # b+. Vì trong trường hợp này xi (được giả định là kỳ vọng của Xi) không ở trung tâm của khoảng a– đến a+, phân bố xác suất của Xi không đều trong toàn bộ khoảng. Tuy nhiên, có thể không có đủ thông tin cho phép lựa chọn một phân bố phù hợp; các mô hình khác nhau sẽ dẫn tới biểu thức khác nhau cho phương sai. Do sự thiếu thông tin như vậy, phép tính gần đúng đơn giản nhất là:
![]() (12)
(12)
Là phương sai của phân bố chữ nhật với độ rộng đầy đủ b+ + b– (Phân bố bất đối xứng cũng được thảo luận trong F.2.4.4 và G.5.3).
VÍ DỤ: Nếu trong Ví dụ 1 của 4.3.7, giá trị của hệ số được cho trong sổ tay là a20(Cu) = 16,52 x 10-6 0C-1 và được quy định rằng “giá trị nhỏ nhất có thể là 16,40 x 10-6 0C-1 và giá trị lớn nhất có thể là 16,92 x 10-6 0C-1” khi đó b– =0,12 x 10-6 0C-1, b+ = 0,40 x 10-6 0C-1, và, từ Phương trình (8), u(a20) = 0,15 x 10-6 0C-1.
CHÚ THÍCH 1: Trong nhiều tình huống đo thực tế khi các biên bất đối xứng, có thể thích hợp để áp dụng sự hiệu chính cho ước lượng xi về độ lớn (b+ – b–)/2 do đó ước lượng mới x’i của Xi là ở điểm giữa của các biên: x’i = (a– + a+)/2. Điều này đưa đến tình huống về trường hợp của 4.3.7, với các giá trị mới b’+ =b’– = (b+ + b–)/2 = (a+ + a–)/2 = a.
CHÚ THÍCH 2: Dựa trên nguyên tắc entropy cực đại, hàm mật độ xác suất trong trường hợp bất đối xứng có thể được chỉ ra là p(Xi) = A exp [-l(Xi – xi)], với A = [b–exp(lb+) + b+ – exp(-lb+)]-1 và l={exp[l(b– + b+)]-1}/{b–exp[l(b–+b+)]+b+}. Điều này dẫn đến phương sai u2(xi) = b+b– – (b+ – b–)/l; với b+ > b–, l > 0 và với b+ < b–, l < 0.
4.3.9. Trong 4.3.7, do không có hiểu biết cụ thể về các giá trị có thể có của Xi trong biên ước lượng a– đến a+ nên chỉ có thể giả định là có cùng xác suất để Xi có thể lấy bất kỳ giá trị nào trong các biên đó, với xác suất nằm ngoài bằng “không”. Sự không liên tục của hàm bậc thang như trên trong phân bố xác suất thường là phi vật lý. Trong nhiều trường hợp, thực tế hơn khi dự kiến rằng giá trị gần các biên là ít có khả năng hơn giá trị gần điểm giữa. Do đó có cơ sở để thay thế phân bố chữ nhật đối xứng bằng phân bố hình thang đối xứng có các cạnh có độ dốc (hình thang cân), độ rộng của đáy dưới a+ – a– = 2a và độ rộng của đáy trên bằng 2ab, trong đó 0 £ b £ 1. Khi b -> 1, phân bố hình thang này tiến gần đến phân bố hình chữ nhật của 4.3.7, trong khi với b = 0, nó là phân bố hình tam giác [xem 4.4.6 và Hình 2b)]. Giả định Xi có phân bố hình thang, tìm được kỳ vọng của Xi là xi = (a– + a+)/2 và phương sai đi kèm là
u2(xi) = a2(1 + b2)/6 (9a)
trở thành phân bố hình tam giác với b = 0,
u2(xi) = a2/6 (9b)
CHÚ THÍCH 1: Đối với phân bố chuẩn có kỳ vọng m và độ lệch chuẩn s, khoảng m ± 3s phủ xấp xỉ 99,73% phân bố. Do đó, nếu biên trên và dưới a+ và a– xác định giới hạn 99,73% chứ không phải giới hạn 100% và Xi có thể được giả định là có phân bố xấp xỉ chuẩn hơn là không có hiểu biết cụ thể về Xi giữa các biên như trong 4.3.7 khi đó u2(xi) = a2/9. Bằng cách so sánh, phương sai của phân bố chữ nhật đối xứng của một nửa độ rộng a bằng a2/3 [Phương trình (7)] và của phân bố hình tam giác đối xứng của một nửa độ rộng a bằng a2/6 [Phương trình (9b)]. Độ lớn của phương sai của ba phân bố trên giống nhau xét về sự khác nhau nhiều về lượng thông tin được yêu cầu để giải thích chúng.
CHÚ THÍCH 2: Phân bố hình thang tương đương với phép chập hai phân bố chữ nhật [10], một phân bố với nửa độ rộng a1 bằng nửa độ rộng trung bình của hình thang, a1 = a(1+b)/2 và phân bố kia với nửa độ rộng a2 bằng độ rộng trung bình một trong các cạnh tam giác của hình thang, a2 = a(1-b)/2. Phương sai của phân bố này là ![]() . Phân bố chập có thể hiểu là phân bố chữ nhật có độ rộng 2a1 với độ không đảm bảo được đại diện bởi phân bố hình chữ nhật có độ rộng 2a2 và mô hình hóa thực tế là các biên đại lượng đầu vào không biết chính xác. Nhưng thậm chí nếu a2 rộng bằng 30% của a1 thì u vượt a1/
. Phân bố chập có thể hiểu là phân bố chữ nhật có độ rộng 2a1 với độ không đảm bảo được đại diện bởi phân bố hình chữ nhật có độ rộng 2a2 và mô hình hóa thực tế là các biên đại lượng đầu vào không biết chính xác. Nhưng thậm chí nếu a2 rộng bằng 30% của a1 thì u vượt a1/![]() ít hơn 5%.
ít hơn 5%.
4.3.10. Điều quan trọng là không “tính hai lần” các thành phần độ không đảm bảo. Nếu thành phần của độ không đảm bảo xuất hiện từ ảnh hưởng cụ thể thu được từ đánh giá Loại B thì cần được tính đến như là thành phần độ không đảm bảo độc lập trong phép tính độ không đảm bảo chuẩn tổng hợp của kết quả đo chỉ trong phạm vi ảnh hưởng đó mà không đóng góp vào độ biến động quan trắc được của các quan trắc. Điều này là bởi vì độ không đảm bảo do phần ảnh hưởng góp phần vào độ biến động quan trắc được đã bao gồm trong thành phần của độ không đảm bảo thu được từ phân tích thống kê các quan trắc.
4.3.11. Thảo luận về đánh giá độ không đảm bảo chuẩn Loại B trong các điều kiện từ 4.3.3 tới 4.3.9 chỉ có ý nghĩa chỉ dẫn. Ngoài ra, các đánh giá độ không đảm bảo cần dựa trên dữ liệu định lượng tới phạm vi tối đa có thể, như được nhấn mạnh trong 3.4.1 và 3.4.2.
4.4. Minh họa bằng đồ thị đánh giá độ không đảm bảo chuẩn
4.4.1. Hình 1 miêu tả sự ước lượng giá trị đại lượng đầu vào Xi và sự đánh giá độ không đảm bảo của ước lượng đó từ phân bố chưa biết các giá trị đo có thể có của Xi hoặc phân bố xác suất của Xi được lấy mẫu bằng trung bình các quan trắc lặp lại.
4.4.2. Trong Hình 1a), giả định rằng đại lượng đầu vào Xi là nhiệt độ t, phân bố chưa biết là phân bố chuẩn với kỳ vọng m = 1000C và độ lệch chuẩn s = 1,50C. Khi đó hàm mật độ xác suất (xem C.2.14) là:
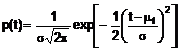
CHÚ THÍCH: Định nghĩa hàm mật độ xác suất p(z) yêu cầu thỏa mãn ![]() .
.
4.4.3. Hình 1b) chỉ ra biểu đồ tần suất của n = 20 quan trắc lặp lại tk của nhiệt độ t giả định được lấy ngẫu nhiên từ phân bố của Hình 1a). Để đạt được biểu đồ tần suất, 20 quan trắc hoặc mẫu, có giá trị cho trong Bảng 1, được nhóm vào trong các khoảng rộng 10C. (Tất nhiên, việc chuẩn bị biểu đồ tần suất không yêu cầu phân tích thống kê số liệu).
Bảng 1 – Hai mươi quan trắc lặp lại nhiệt độ t được nhóm trong các khoảng 1oC
|
Khoảng |
Nhiệt độ t / oC |
|
|
t1 / oC |
t2/oC |
|
|
94,5 |
95,5 |
– |
|
95,5 |
96,5 |
– |
|
96,5 |
97,6 |
96,90 |
|
97,5 |
98,5 |
98,18; 98,25 |
|
98,5 |
99,5 |
98,61; 99,03; 99,49 |
|
99,5 |
100,5 |
99,56; 99,74; 99,89; 100,07; 100,33; 100,42 |
|
100,5 |
101,5 |
100,68; 100,95; 101,11; 101,20 |
|
101,5 |
102,5 |
101,57; 101,84; 102,36 |
|
102,5 |
103,5 |
102,72 |
|
103,5 |
104,5 |
– |
|
104,5 |
105,5 |
– |
Trung bình cộng hoặc trung bình t của n = 20 quan trắc được tính theo Phương trình (3) là ![]() và được giả định là ước lượng tốt nhất của kỳ vọng mt của t dựa trên dữ liệu có sẵn. Độ lệch chuẩn thực nghiệm s(tk) được tính từ Phương trình (4) là s(tk) = 1,4890C » 1,490C và độ lệch chuẩn thực nghiệm của trung bình s(
và được giả định là ước lượng tốt nhất của kỳ vọng mt của t dựa trên dữ liệu có sẵn. Độ lệch chuẩn thực nghiệm s(tk) được tính từ Phương trình (4) là s(tk) = 1,4890C » 1,490C và độ lệch chuẩn thực nghiệm của trung bình s(![]() ) được tính từ Phương trình (5), là độ không đảm bảo u(
) được tính từ Phương trình (5), là độ không đảm bảo u(![]() ) của trung bình
) của trung bình ![]() , bằng u(
, bằng u(![]() ) = s(
) = s(![]() ) = s(tk)/
) = s(tk)/![]() = 0,3330C » 0,330C. (Với các phép tính tiếp theo, gần như tất cả các chữ số được giữ lại).
= 0,3330C » 0,330C. (Với các phép tính tiếp theo, gần như tất cả các chữ số được giữ lại).
CHÚ THÍCH: Mặc dù dữ liệu trong Bảng 1 có vẻ hợp lý khi tính đến việc sử dụng phổ biến nhiệt kế điện tử kỹ thuật số có độ phân giải cao nhưng chúng được dùng cho mục đích minh họa và không nhất thiết được hiểu như mô tả phép đo thực sự.
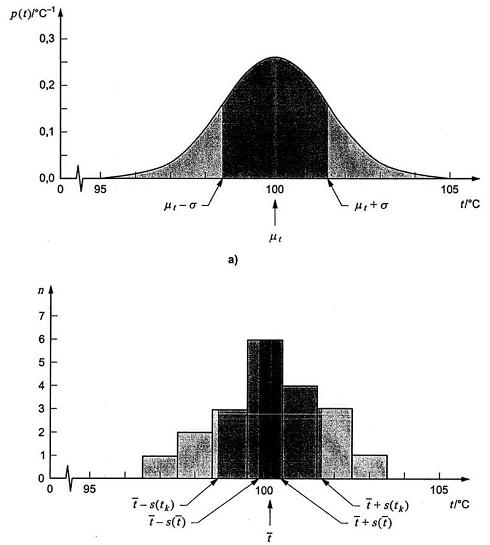
b)
Hình 1 – Minh họa bằng đồ thị đánh giá độ không đảm bảo chuẩn của đại lượng đầu vào từ các quan trắc lặp lại
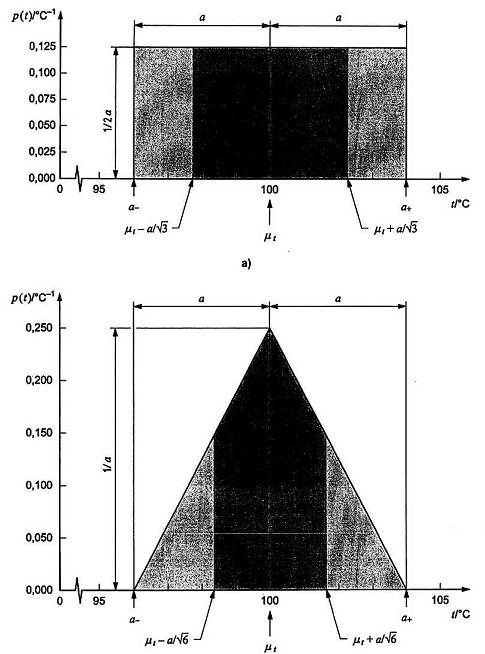
b)
Hình 1 – Minh họa bằng đồ thị đánh giá độ không đảm bảo chuẩn của đại lượng đầu vào từ phân bố tiên nghiệm
4.4.4. Hình 2 thể hiện ước lượng giá trị đại lượng đầu vào Xi và đánh giá độ không đảm bảo của ước lượng đó từ phân bố tiên nghiệm các giá trị có thể có của Xi hoặc phân bố xác suất của Xi dựa trên tất cả thông tin có sẵn. Đối với cả hai trường hợp được trình bày, đại lượng đầu vào được giả định là nhiệt độ t.
4.4.5. Đối với trường hợp minh họa trong Hình 2a), giả định rằng có ít thông tin về đại lượng đầu vào t và chữ có thể giả định t được mô tả bằng phân bố xác suất đối xứng, chữ nhật và tiên nghiệm của biên dưới a– = 960C, biên trên a+ = 1040C và do đó nửa độ rộng a = (a+ + a–)/2 = 40C (xem 4.3.7). Khi đó, hàm mật độ xác suất của t là:
p(t) = 1/(2a), a– £ t £ a+,
p(t) = 0 trường hợp khác.
Như được trình bày trong 4.3.7, ước lượng tốt nhất của t là kỳ vọng của nó mt = (a+ + a–)/2 = 1000C, tiếp theo C.3.1. Độ không đảm bảo chuẩn của ước lượng này là u(mt) = a /![]() » 2,30C, tiếp theo C.3.2 [xem Phương trình (7)].
» 2,30C, tiếp theo C.3.2 [xem Phương trình (7)].
4.4.6. Với trường hợp minh họa trong Hình 2b), giả định thông tin có sẵn về t ít hạn chế hơn và t được mô tả bằng phân bố xác suất đối xứng, tam giác và tiên nghiệm của cùng biên dưới a– = 960C, cùng biên trên a+ = 1040C và do đó nửa độ rộng a = (a+ + a–)/2 = 40C như trong 4.4.5 (xem 4.3.9). Khi đó, hàm mật độ xác suất của t là:
p(t) = (t – a–)/a2, a– £ t £ (a+ + a–)/2
p(t) = (a+ – t)/a2, (a+ + a–)/2 £ t £ a+
p(t) = 0 trường hợp khác.
Như được trình bày trong 4.3.9, kỳ vọng của t là mt = (a+ + a–)/2 = 1000C, suy ra từ C.3.1. Độ không đảm bảo chuẩn của ước lượng này là u(mt) = a/![]() » 1,60C, suy ra từ C.3.2 [xem Phương trình 9b)].
» 1,60C, suy ra từ C.3.2 [xem Phương trình 9b)].
Giá trị trên, u(mt) = 1,60C, có thể được so sánh với u(mt) = 2,30C thu được trong 4.4.5 từ phân bố chữ nhật có cùng độ rộng 80C; với s = 1,50C có phân bố chuẩn ở Hình 1a) có độ rộng từ -2,58s đến +2,58s; bao gồm 99% của phân bố, gần 80C; và với u(![]() ) = 0,330C thu được trong 4.4.3 từ 20 quan trắc được giả định là lấy ngẫu nhiên từ cùng phân bố chuẩn.
) = 0,330C thu được trong 4.4.3 từ 20 quan trắc được giả định là lấy ngẫu nhiên từ cùng phân bố chuẩn.
5. Xác định độ không đảm bảo chuẩn tổng hợp
5.1. Đại lượng đầu vào không tương quan
Điều này xử lý trường hợp tất cả các đại lượng đầu vào là độc lập (C.3.7). Trường hợp hai hoặc nhiều đại lượng đầu vào có liên quan, phụ thuộc nhau hoặc tương quan (C.2.8), được trình bày trong 5.2.
5.1.1. Độ không đảm bảo chuẩn của y, trong đó y là ước lượng của đại lượng do Y và do đó kết quả đo, thu được bằng cách kết hợp thích hợp độ không đảm bảo chuẩn của ước lượng đầu vào x1, x2, …, xN (xem 4.1). Độ không đảm bảo chuẩn tổng hợp này của ước lượng y được ký hiệu là uc(y).
CHÚ THÍCH: Vì lý do tương tự như trong chú thích của 4.3.1, ký hiệu uc(y) và u![]() (y) được sử dụng trong tất cả các trường hợp.
(y) được sử dụng trong tất cả các trường hợp.
5.1.2. Độ không đảm bảo chuẩn tổng hợp uc(y) là dương căn bậc hai của phương sai tổng hợp u![]() (y), được cho bằng:
(y), được cho bằng:
![]() (10)
(10)
Trong đó f là hàm được cho trong Phương trình (1). Mỗi u(xi) là độ không đảm bảo chuẩn được đánh giá như mô tả trong 4.2 (đánh giá Loại A) hoặc như trong 4.3 (đánh giá Loại B). Độ không đảm bảo chuẩn tổng hợp uc(y) là độ không đảm bảo ước lượng mô tả sự phân tán của các giá trị có thể có được quy cho đại lượng đo Y một cách hợp lý (xem 2.2.3).
Phương trình (10) và bản khác của nó đối với đại lượng đầu vào tương quan là, Phương trình (13) đều dựa trên phép tính gần đúng chuỗi Taylor bậc nhất của Y = f(X1, X2, …, XN), thể hiện những gì được gọi là định luật lan truyền độ không đảm bảo trong tiêu chuẩn này (xem E.3.1 và E.3.2).
CHÚ THÍCH: Khi tính phi tuyến của f là đáng kể thì các số hạng có bậc cao hơn trong khai triển chuỗi Taylor phải được tính đến trong biểu thức u![]() (y), Phương trình (10). Khi phân bố của mỗi Xi là chuẩn thì các số hạng quan trọng nhất của bậc cao nhất tiếp theo được cộng vào các số hạng của Phương trình (10) là:
(y), Phương trình (10). Khi phân bố của mỗi Xi là chuẩn thì các số hạng quan trọng nhất của bậc cao nhất tiếp theo được cộng vào các số hạng của Phương trình (10) là:
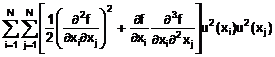
Xem H.1 đối với ví dụ về trường hợp cần xem xét đóng góp của các số hạng bậc cao hơn vào u![]() (y).
(y).
5.1.3. Đạo hàm riêng ![]() /
/![]() bằng
bằng ![]() /
/![]() được lấy tại Xi = xi (Xem chú thích1 ở dưới). Các đạo hàm này, thường được gọi là các hệ số nhạy, mô tả cách ước lượng đầu ra y biến đổi thế nào theo các thay đổi giá trị của ước lượng đầu vào x1, x2, …, xN. Đặc biệt, sự thay đổi về y do thay đổi nhỏ ∆xi gây ra trong ước lượng đầu vào xi được cho bởi (∆y)i = (
được lấy tại Xi = xi (Xem chú thích1 ở dưới). Các đạo hàm này, thường được gọi là các hệ số nhạy, mô tả cách ước lượng đầu ra y biến đổi thế nào theo các thay đổi giá trị của ước lượng đầu vào x1, x2, …, xN. Đặc biệt, sự thay đổi về y do thay đổi nhỏ ∆xi gây ra trong ước lượng đầu vào xi được cho bởi (∆y)i = (![]() /
/![]() )(∆xi). Nếu thay đổi này được tạo ra do độ không đảm bảo chuẩn của ước lượng xi thì biến động tương ứng trong y là (
)(∆xi). Nếu thay đổi này được tạo ra do độ không đảm bảo chuẩn của ước lượng xi thì biến động tương ứng trong y là (![]() /
/![]() ) u(xi). Do đó, phương sai tổng hợp u
) u(xi). Do đó, phương sai tổng hợp u![]() (y) có thể được xem là tổng các số hạng, mỗi số hạng đại diện cho phương sai ước lượng đi kèm ước lượng đầu ra y được tạo ra bởi phương sai ước lượng đi kèm mỗi ước lượng đầu vào xi. Điều này gợi ý viết Phương trình (10) như sau:
(y) có thể được xem là tổng các số hạng, mỗi số hạng đại diện cho phương sai ước lượng đi kèm ước lượng đầu ra y được tạo ra bởi phương sai ước lượng đi kèm mỗi ước lượng đầu vào xi. Điều này gợi ý viết Phương trình (10) như sau:
![]() (11a)
(11a)
Trong đó:
ci = ![]() /
/![]() , ui(y) = |ci|u(xi) (11b)
, ui(y) = |ci|u(xi) (11b)
CHÚ THÍCH: Nói đúng ra, các hàm riêng là![]() /
/![]() =
= ![]() /
/![]() được đánh giá ở các kỳ vọng của Xi. Tuy nhiên, trong thực tế, đạo hàm riêng được ước lượng bằng:
được đánh giá ở các kỳ vọng của Xi. Tuy nhiên, trong thực tế, đạo hàm riêng được ước lượng bằng:
![]()
CHÚ THÍCH 2: Độ không đảm bảo chuẩn tổng hợp uc(y) có thể được tính bằng số bằng cách thay thế ciu(xi) trong Phương trình (11a) bằng:
Zi = ![]() {f[x1,…,xi + u(xi), …, xN)] – f[x1, …, xi – u(xi), …, xN]}
{f[x1,…,xi + u(xi), …, xN)] – f[x1, …, xi – u(xi), …, xN]}
Nghĩa là ui(y) được đánh giá bằng số bằng cách tính sự thay đổi trong y do thay đổi trong xi của +u(xi) và -u(xi). Giá trị ui(y) khi đó có thể lấy bằng |Zi| và giá trị của hệ số nhạy tương ứng ci bằng Zi/u(xi).
VÍ DỤ: Ví dụ của 4.1.1, để đơn giản, sử dụng ký hiệu giống nhau cho cả đại lượng và ước lượng của nó,
c1 = ![]() = 2V/{Ro[1+a(t-to)]} = 2P/V
= 2V/{Ro[1+a(t-to)]} = 2P/V
c2 = ![]() = -V2/{R
= -V2/{R![]() [1+a(t-to)]} = -P/Ro
[1+a(t-to)]} = -P/Ro
c3 = ![]() = -V2(t – to)/{Ro[1+a(t – to)]2} = -P(t – to)/[1 + a(t – to)]
= -V2(t – to)/{Ro[1+a(t – to)]2} = -P(t – to)/[1 + a(t – to)]
c4 = ![]() = -V2a/{Ro[1+a(t – to)]2} = -Pa/[1 + a(t – to)]
= -V2a/{Ro[1+a(t – to)]2} = -Pa/[1 + a(t – to)]
và
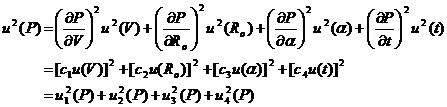
5.1.4. Thay vì tính từ hàm f, hệ số nhạy ![]() /
/![]() đôi khi được xác định bằng thực nghiệm: đo sự thay đổi của Y do sự thay đổi cụ thể của Xi gây ra trong khi giữ các đại lượng đầu vào không đổi. Trong trường hợp này, hiểu biết về hàm f (hoặc phần chia của nó khi chỉ một vài hệ số nhạy được xác định như vậy) sẽ giảm tương ứng theo khai triển chuỗi Taylor đến bậc nhất thực nghiệm dựa trên hệ số nhạy đo được.
đôi khi được xác định bằng thực nghiệm: đo sự thay đổi của Y do sự thay đổi cụ thể của Xi gây ra trong khi giữ các đại lượng đầu vào không đổi. Trong trường hợp này, hiểu biết về hàm f (hoặc phần chia của nó khi chỉ một vài hệ số nhạy được xác định như vậy) sẽ giảm tương ứng theo khai triển chuỗi Taylor đến bậc nhất thực nghiệm dựa trên hệ số nhạy đo được.
5.1.5. Nếu Phương trình (1) cho đại lượng đo Y được triển khai xấp xỉ giá trị danh nghĩa Xi,0 của đại lượng đầu vào Xi thì bậc nhất (thường là phép tính gần đúng thích hợp) Y = Yo + c1d1 + c2d2 + … + cNdN, trong đó Y0 = f(X1,0, X2,0, …, XN,0), ci = (![]() được đánh giá ở Xi = Xi,0 và di = Xi – Xi,0. Do đó, với mục đích phân tích độ không đảm bảo, đại lượng đo thường tính xấp xỉ bằng hàm tuyến tính của các biến của nó bằng cách biến đổi các đại lượng đầu vào từ Xi tới di (xem E.3.1).
được đánh giá ở Xi = Xi,0 và di = Xi – Xi,0. Do đó, với mục đích phân tích độ không đảm bảo, đại lượng đo thường tính xấp xỉ bằng hàm tuyến tính của các biến của nó bằng cách biến đổi các đại lượng đầu vào từ Xi tới di (xem E.3.1).
VÍ DỤ: Từ ví dụ 2 của 4.3.7, ước lượng của giá trị đại lượng đo V là ![]() , trong đó
, trong đó ![]() = 0,928 571 V, u(
= 0,928 571 V, u(![]() ) = 12mV, sự hiệu chính bổ sung
) = 12mV, sự hiệu chính bổ sung ![]() = 0 và u(
= 0 và u(![]() ) = 8,7mV. Vì
) = 8,7mV. Vì ![]() =1 và
=1 và ![]() = 1 nên phương sai tổng hợp kèm theo V được cho bằng:
= 1 nên phương sai tổng hợp kèm theo V được cho bằng:
![]()
Và độ không đảm bảo chuẩn tổng hợp là uc(V) = 15mV, tương ứng với độ không đảm bảo chuẩn tổng hợp tương đối uc(V)/V bằng 16 x 10-6 (xem 5.1.6). Đây là ví dụ của trường hợp đại lượng đo đã là hàm tuyến tính các của các đại lượng mà nó phụ thuộc, với hệ số ci = +1. Theo Phương trình (10) nếu Y = c1X1 + c2X2 + … + cNXN và nếu hằng số ci = +1 hoặc -1 thì ![]() .
.
5.1.6. Nếu Y ở dạng ![]() và số mũ pi là dương hoặc âm đã biết có độ không đảm bảo không đáng kể, thì phương sai tổng hợp, Phương trình (10), có thể được thể hiện là:
và số mũ pi là dương hoặc âm đã biết có độ không đảm bảo không đáng kể, thì phương sai tổng hợp, Phương trình (10), có thể được thể hiện là:
[uc(y)/y]2 = ![]() (12)
(12)
Phương trình này có cùng dạng với Phương trình (11a) nhưng với phương sai tổng hợp ![]() được thể hiện như phương sai tổng hợp tương đối [uc(y)/y]2 và phương sai ước lượng u2(xi) kèm theo từng ước lượng đầu vào được thể hiện như phương sai tương đối ước lượng [uc(xi)/xi]2. [Độ không đảm bảo chuẩn tổng hợp tương đối là uc(y)/|y| và độ không đảm bảo chuẩn tương đối của từng ước lượng đầu vào là u(xi)/|xi|, |y| # 0 và |xi| # 0.]
được thể hiện như phương sai tổng hợp tương đối [uc(y)/y]2 và phương sai ước lượng u2(xi) kèm theo từng ước lượng đầu vào được thể hiện như phương sai tương đối ước lượng [uc(xi)/xi]2. [Độ không đảm bảo chuẩn tổng hợp tương đối là uc(y)/|y| và độ không đảm bảo chuẩn tương đối của từng ước lượng đầu vào là u(xi)/|xi|, |y| # 0 và |xi| # 0.]
CHÚ THÍCH 1: Khi Y có dạng này thì phép biến đổi thành hàm tuyến tính của các biến (xem 5.1.5) dễ dàng thực hiện được bằng cách đặt Xi = Xi,0(1 + di), từ đó quan hệ gần đúng sẽ là: (Y – Y0)/Y0 = ![]() . Mặt khác, phép biến đổi logarit Z = lnY và Wi = ln Xi dẫn tới tuyến tính hóa chính xác theo các biến đổi: Z = ln c +
. Mặt khác, phép biến đổi logarit Z = lnY và Wi = ln Xi dẫn tới tuyến tính hóa chính xác theo các biến đổi: Z = ln c + ![]() .
.
CHÚ THÍCH 2: Nếu mỗi pi là +1 hoặc -1, Phương trình (12) trở thành [uc(y)/y]2 =![]() , đối với trường hợp cụ thể này, nó chỉ ra rằng phương sai tổng hợp tương đối gắn với ước lượng y đơn giản bằng tổng các phương sai tương đối ước lượng gắn với các ước lượng đầu vào xi.
, đối với trường hợp cụ thể này, nó chỉ ra rằng phương sai tổng hợp tương đối gắn với ước lượng y đơn giản bằng tổng các phương sai tương đối ước lượng gắn với các ước lượng đầu vào xi.
5.2. Các đại lượng đầu vào tương quan
5.2.1. Phương trình (10) và những dẫn xuất từ đó như Phương trình (11a) và (12) chỉ có giá trị nếu các đại lượng đầu vào Xi độc lập hay không tương quan (các biến ngẫu nhiên, không phải đại lượng vật lý được giả định là bất biến – xem 4.1.1, Chú thích 1). Nếu một số trong Xi tương quan đáng kể thì sự tương quan phải được tính đến.
5.2.2. Khi các đại lượng đầu vào tương quan thì biểu thức phù hợp đối với phương sai tổng hợp ![]() kèm theo kết quả đo là:
kèm theo kết quả đo là:
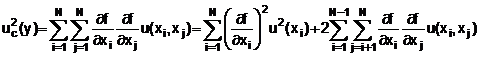 (13)
(13)
Trong đó xi và xj là các ước lượng của Xi và Xj, còn u(xi,xj) = u(xj,xi) là hiệp phương sai ước lượng kèm theo xi và xj. Mức độ tương quan giữa xi và xj được đặc trưng bởi hệ số tương quan ước lượng (C.3.6).
![]() (14)
(14)
Trong đó r(xi,xj) = r(xj,xi) và -1 £ r(xi,xj) £ +1. Nếu các ước lượng xi và xj độc lập thì r(xi,xj) = 0 và một ước lượng thay đổi không có nghĩa là ước lượng khác thay đổi. (Xem thảo luận thêm trong C.2.8, C.3.6 và C.3.7)
Về hệ số tương quan, dễ hiểu hơn hiệp phương sai, số hạng hiệp phương sai của Công thức (13) có thể được viết là:
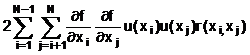 (15)
(15)
Khi đó, sử dụng (11b), Phương trình (13) trở thành:
![]() (16)
(16)
CHÚ THÍCH 1: Đối với trường hợp rất đặc biệt khi tất cả ước lượng đầu vào tương quan với hệ số tương quan r(xi,xj) = +1, Phương trình (16) rút gọn thành:
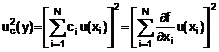
Do đó độ không đảm bảo chuẩn tổng hợp uc(y) đơn giản là tổng tuyến tính các số hạng đại diện cho biến động của ước lượng đầu ra y được sinh ra bởi độ không đảm bảo chuẩn của mỗi ước lượng đầu vào (xem 5.1.3). [không nên nhầm tổng tuyến tính này với quy luật chung về lan truyền sai số dù nó có dạng tương tự; độ không đảm bảo chuẩn không phải là sai số (xem E.3.2)]
VÍ DỤ: Mười điện trở, mỗi giá trị danh nghĩa Ri = 1 000 W được hiệu chuẩn với độ không đảm bảo không đáng kể bằng so sánh với cùng điện trở chuẩn 1 000 W Rs được đặc trưng bằng độ không đảm bảo chuẩn u(Rs) = 100 mW như đã cho trong giấy chứng nhận hiệu chuẩn. Các điện trở được mắc nối tiếp với dây có điện trở không đáng kể để thu được điện trở quy chiếu Rref có giá trị danh nghĩa 10 kW. Do đó, Rref = f(Ri) = ![]() . Vì r(xi,xj) = r(Ri,Rj) = +1 đối với mỗi cặp điện trở (xem F.1.2.3, ví dụ 2) nên áp dụng được phương trình của chú thích này. Khi với mỗi điện trở
. Vì r(xi,xj) = r(Ri,Rj) = +1 đối với mỗi cặp điện trở (xem F.1.2.3, ví dụ 2) nên áp dụng được phương trình của chú thích này. Khi với mỗi điện trở ![]() và u(xi)= u(Ri) = u(Rs) (xem F.1.2.3, Ví dụ 2), nên phương trình đó mang lại cho độ không đảm bảo chuẩn tổng hợp của Rref, uc(Rref) =
và u(xi)= u(Ri) = u(Rs) (xem F.1.2.3, Ví dụ 2), nên phương trình đó mang lại cho độ không đảm bảo chuẩn tổng hợp của Rref, uc(Rref) = ![]() = 10 x (100 mW) = 1W. Kết quả uc(Rref) = [
= 10 x (100 mW) = 1W. Kết quả uc(Rref) = [![]() ]1/2 = 0,32W thu được từ Phương trình (10) là không đúng vì nó không tính đến việc tất cả các giá trị được hiệu chuẩn của mười điện trở có mối tương quan.
]1/2 = 0,32W thu được từ Phương trình (10) là không đúng vì nó không tính đến việc tất cả các giá trị được hiệu chuẩn của mười điện trở có mối tương quan.
CHÚ THÍCH 2: Phương sai ước lượng u2(xi) và hiệp phương sai ước lượng u(xi,xj) có thể coi là các phân tử của ma trận hiệp phương sai với các phân tử uij. Các phân tử đường chéo uij của ma trận là các phương sai u2(xi), trong khi các phần tử ngoài đường chéo uij (i # j) là các hiệp phương sai u(xi,xj) = u(xj,xi). Nếu hai ước lượng đầu vào không tương quan thì hiệp phương sai kèm theo của chúng và các phần tử tương ứng uij và uji của ma trận phương sai bằng 0. Nếu các ước lượng đầu vào đều không tương quan thì tất cả các phần tử ngoài đường chéo bằng “không” và ma trận hiệp phương sai là ma trận đường chéo. (Xem thêm C.3.5).
CHÚ THÍCH 3: Với mục đích đánh giá bằng số, Phương trình (16) có thể viết là:
![]()
Trong đó Zi được cho trong 5.1.3, Chú thích 2.
CHÚ THÍCH 4: Nếu Xi có dạng đặc biệt được xem xét trong 5.1.6 có tương quan thì phải thêm vào vế phải của Phương trình (12) các số hạng
![]()
5.2.3. Xét hai trung bình cộng ![]() và
và ![]() ước lượng kỳ vọng mq và mr của hai đại lượng biến đổi ngẫu nhiên q và r, và để
ước lượng kỳ vọng mq và mr của hai đại lượng biến đổi ngẫu nhiên q và r, và để ![]() và
và ![]() được tính từ n cập quan trắc đồng thời độc lập của q và r thực hiện trong cùng điều kiện đo (xem B.2.15). Khi đó hiệp phương sai (xem C.3.4) của
được tính từ n cập quan trắc đồng thời độc lập của q và r thực hiện trong cùng điều kiện đo (xem B.2.15). Khi đó hiệp phương sai (xem C.3.4) của ![]() và
và ![]() được ước lượng bằng:
được ước lượng bằng:
![]() (17)
(17)
Trong đó qk và rk là các quan trắc riêng lẻ của các đại lượng q và r, còn ![]() và
và ![]() được tính từ các quan trắc theo Phương trình (3). Nếu thực tế các quan trắc không tương quan thì hiệp phương sai tính được kỳ vọng gần bằng 0.
được tính từ các quan trắc theo Phương trình (3). Nếu thực tế các quan trắc không tương quan thì hiệp phương sai tính được kỳ vọng gần bằng 0.
Do đó hiệp phương sai ước lượng của hai đại lượng đầu vào tương quan Xi và Xj được ước lượng bằng, trung bình ![]() và
và ![]() xác định từ các cặp quan trắc đồng thời lặp lại độc lập cho bởi u(xi,xj) = s(
xác định từ các cặp quan trắc đồng thời lặp lại độc lập cho bởi u(xi,xj) = s(![]() ,
,![]() ), với s(
), với s(![]() ,
,![]() ) được tính theo Phương trình (17). Việc áp dụng Phương trình (17) này là đánh giá hiệp phương sai Loại A. Hệ số tương quan ước tính của
) được tính theo Phương trình (17). Việc áp dụng Phương trình (17) này là đánh giá hiệp phương sai Loại A. Hệ số tương quan ước tính của ![]() và
và ![]() thu được từ Phương trình (14): r(xi,xj) = r(
thu được từ Phương trình (14): r(xi,xj) = r(![]() ,
,![]() ) = s(
) = s(![]() ,
,![]() )/[s(
)/[s(![]() ),s(
),s(![]() )].
)].
CHÚ THÍCH: Các ví dụ khi cần sử dụng hiệp phương sai như tính toán trong Phương trình (17) được cho trong H.2 và H.4.
5.2.4. Có thể có sự tương quan đáng kể giữa hai đại lượng đầu vào nếu sử dụng cùng phương tiện đó, chuẩn đo lường vật lý hoặc số liệu tra cứu có độ không đảm bảo chuẩn đáng kể giống nhau để xác định chúng. Ví dụ, nếu sử dụng nhiệt kế nhất định để xác định sự hiểu chỉnh nhiệt độ được yêu cầu cho việc ước lượng giá trị đại lượng đầu vào Xi và sử dụng chính nhiệt kế đó để xác định sự hiệu chính nhiệt độ tương tự được yêu cầu cho ước lượng đại lượng đầu vào Xj, thì hai đại lượng đầu vào này có thể có tương quan đáng kể. Tuy nhiên, nếu Xi và Xj trong ví dụ này được xác định lại là các đại lượng chưa hiệu chính và các đại lượng này xác định đường cong hiệu chuẩn của nhiệt kế được tính đến như đại lượng đầu vào bổ sung với độ không đảm bảo chuẩn độc lập, thì mối tương quan giữa Xi và Xj được loại bỏ. (Xem thảo luận cụ thể trong F.1.2.3 và F.1.2.4).
5.2.5. Sự tương quan giữa các đại lượng đầu vào không thể bỏ qua nếu có và đáng kể. Hiệp phương sai kèm theo cần được đánh giá bằng thực nghiệm nếu khả thi bằng cách thay đổi các đại lượng đầu vào tương quan (xem C.3.6, Chú thích 3) hoặc sử dụng tổ hợp thông tin có sẵn về biến thiên tương quan của đại lượng đang xét (đánh giá hiệp phương sai Loại B). Sự thông hiểu dựa trên kinh nghiệm và hiểu biết chung (xem 4.3.1 và 4.3.2) đặc biệt khi cần ước lượng mức độ tương quan giữa các đại lượng đầu vào xuất hiện từ tác động của ảnh hưởng chung, như nhiệt độ môi trường, áp suất khí quyển và độ ẩm. May mắn là trong nhiều trường hợp, ảnh hưởng của các tác động trên có sự phụ thuộc không đáng kể và các đại lượng đầu vào chịu tác động có thể được giả định là không tương quan. Tuy nhiên, nếu chúng không thể được giả định là không tương quan thì bản thân sự tương quan có thể tránh được nếu các ảnh hưởng phổ biến được đưa ra như đại lượng đầu vào độc lập bổ sung như được trình bày trong 5.2.4.
6. Xác định độ không đảm bảo mở rộng
6.1. Giới thiệu
6.1.1. Khuyến nghị INC-1 (1980) của nhóm công tác về Trình bày độ không đảm bảo làm cơ sở cho tiêu chuẩn này (xem Lời giới thiệu), Khuyến nghị 1 (CI-1981) và 1 (CI-1986) của CIPM thông qua và xác nhận lại INC-1 (1980) (xem A.2 và A.3) tán thành việc sử dụng độ không đảm bảo chuẩn tổng hợp uc(y) là tham số thể hiện định lượng độ không đảm bảo của kết quả đo. Thực vậy, trong khuyến nghị thứ hai, CIPM đã yêu cầu rằng những gì được gọi là độ không đảm bảo chuẩn tổng hợp uc(y) được sử dụng “bởi tất cả các bên tham gia trong việc đưa ra kết quả của tất cả các so sánh quốc tế hoặc công tác khác được thực hiện dưới sự bảo trợ của CIPM và Ủy ban Tư vấn”.
6.1.2. Mặc dù có thể uc(y) được sử dụng phổ biến để trình bày độ không đảm bảo của kết quả đo nhưng trong một số ứng dụng thương mại, công nghiệp và quy định, khi liên quan đến sức khỏe và an toàn thì thường cần đưa ra thước đo độ không đảm bảo xác định khoảng bao quanh kết quả đo mà có thể hy vọng chứa phần lớn phân bố các giá trị có thể được quy hợp lý cho đại lượng đo. Yêu cầu này được Nhóm công tác thừa nhận và được đưa ra trong đoạn 5 của Khuyến nghị INC-1 (1980). Nó cũng được phản ánh trong Khuyến nghị 1 (CI – 1986) của CIPM.
6.2. Độ không đảm bảo mở rộng
6.2.1. Thước đo bổ sung độ không đảm bảo đáp ứng yêu cầu cung cấp khoảng thuộc loại được trình bày trong 6.1.2 được gọi là độ không đảm bảo mở rộng và ký hiệu là U. Độ không đảm bảo mở rộng U nhận được bằng cách nhân độ không đảm bảo chuẩn tổng hợp uc(y) với hệ số phủ k:
U = kuc(y) (18)
Khi đó kết quả đo được thể hiện đơn giản là Y = y ± U, được hiểu theo nghĩa ước lượng tốt nhất của giá trị có thể quy cho đại lượng đo Y là y và y – U đến y + U là khoảng có thể hy vọng chứa phần lớn phân bố các giá trị có thể được quy hợp lý cho Y. Khoảng này cũng được trình bày là y – U £ Y £ y + U.
6.2.2. Các thuật ngữ khoảng tin cậy (C.2.27, C.2.28) và mức tin cậy (C.2.29) có định nghĩa riêng trong thống kê và chỉ áp dụng được cho khoảng xác định bởi U khi đáp ứng các điều kiện nhất định, bao gồm tất cả các thành phần của độ không đảm bảo đóng góp vào uc(y) thu được từ đánh giá Loại A.
Do đó, trong tiêu chuẩn này, từ “tin cậy” không được sử dụng để bổ nghĩa cho từ “khoảng” khi đề cập đến khoảng được xác định bởi U. Cụ thể hơn, U được hiểu là xác định khoảng về kết quả đo chứa phần lớn p của phân bố xác suất được đặc trưng bởi kết quả này và độ không đảm bảo chuẩn tổng hợp của nó, và p là xác suất phủ hay mức tin cậy của khoảng đó.
6.2.3. Bất cứ khi nào thực hiện được, mức tin cậy p gắn với khoảng được xác định bởi U cần được ước lượng và mô tả. Cần thừa nhận rằng nhân uc(y) với hằng số không đưa ra thông tin mới nhưng thể hiện thông tin có sẵn trước đây theo hình thức khác. Tuy nhiên, cũng cần thừa nhận rằng trong hầu hết trường hợp, mức tin cậy p (đặc biệt với giá trị p gần bằng 1) khá là không chắc chắn, không chỉ vì hiểu biết hạn chế về phân bố xác suất được đặc trưng bởi y và uc(y) (đặc trưng là ở các phần cực trị) mà còn vì độ không đảm bảo của chính uc(y) (xem Chú thích 2 cho 2.3.5, 6.3.2, 6.3.3 và Phụ lục G, cụ thể là G.6.6).
CHÚ THÍCH: Với các cách mô tả kết quả đo ưu tiên khi thước đo độ không đảm bảo là uc(y) và khi đó là U, tương ứng xem 7.2.2 và 7.2.4.
6.3. Lựa chọn hệ số phủ
6.3.1. Giá trị của hệ số phủ k được chọn trên cơ sở mức tin cậy yêu cầu của khoảng y – U đến y + U. Nói chung, k sẽ trong khoảng 2 đến 3. Tuy nhiên, với các ứng dụng đặc biệt k có thể nằm ngoài khoảng này. Kinh nghiệm bao quát và kiến thức đầy đủ về việc sử dụng mà kết quả đo sẽ được đặt vào có thể tạo thuận lợi cho việc lựa chọn giá trị k thích hợp.
CHÚ THÍCH: Đôi khi, có thể nhận thấy rằng việc hiệu chỉnh b đã biết đối với ảnh hưởng hệ thống đã không được áp dụng cho kết quả đo đã báo cáo nhưng thay vào đó có sự cố gắng để tính đến ảnh hưởng này bằng cách mở rộng “độ không đảm bảo” được ấn định cho kết quả. Điều này cần tránh; chỉ trong những trường hợp rất đặc biệt mới không nên áp dụng sự hiệu chính đối với các ảnh hưởng hệ thống đáng kể đã biết không được áp dụng cho kết quả đo (xem F.2.4.5 đối với trường hợp cụ thể và cách xử lý). Không được nhầm đánh giá độ không đảm bảo của kết quả đo với ấn định giới hạn an toàn cho đại lượng nào đó.
6.3.2. Trường hợp lý tưởng, ta muốn chọn được giá trị hệ số phủ k cụ thể có thể cho khoảng Y = y ± U = y ± k uc(y) tương ứng với mức tin cậy p cụ thể, như 95% hoặc 99%; tương đương đối với giá trị k cho trước, ta muốn nêu rõ được mức tin cậy kèm theo khoảng đó. Tuy nhiên, điều này không dễ thực hiện trong thực tế vì nó đòi hỏi sự hiểu biết bao quát về phân bố xác suất được đặc trưng bởi kết quả đo y và độ không đảm bảo chuẩn tổng hợp uc(y). Mặc dù các tham số này có tầm quan trọng then chốt, nhưng chính chúng không đủ cho mục đích thiết lập khoảng có mức tin cậy đã biết chính xác.
6.3.3. Khuyến nghị INC-1 (1980) không quy định cách thiết lập mối quan hệ giữa k và p. Vấn đề này được thảo luận trong Phụ lục G và phương pháp ưu tiên cho phương pháp xấp xỉ được trình bày trong G.4 và tổng kết trong G.6.4. Tuy nhiên, cách tiếp cận đơn giản hơn, được thảo luận trong G.6.6, thường thích hợp với các tình huống đo mà phân bố xác suất được đặc trưng bởi y và uc(y) là xấp xỉ chuẩn và mức độ hiệu dụng của bậc tự do hiệu dụng của uc(y) có độ lớn đáng kể. Trong trường hợp như vậy, thường xảy ra trong thực tế, có thể giả định rằng lấy k = 2 sẽ tạo ra khoảng có mức tin cậy xấp xỉ 95% và khi lấy k = 3 sẽ tạo ra khoảng có mức tin cậy xấp xỉ 99%.
CHÚ THÍCH: Phương pháp ước lượng bậc tự do hiệu dụng của uc(y) được cho trong G.4. Khi đó Bảng G.2 của Phụ lục G có thể được sử dụng để giúp quyết định nếu giải pháp này phù hợp cho phép đo cụ thể (xem G.6.6).
7. Báo cáo độ không đảm bảo
7.1. Hướng dẫn chung
7.1.1. Nói chung, khi đưa ra hệ thống thứ bậc đo lường phân cấp phép đo thì càng cần nhiều chi tiết hơn về cách thu được kết quả đo và độ không đảm bảo của nó. Tuy nhiên, ở mọi trình độ của hệ thống thứ bậc này, bao gồm các hoạt động thương mại và quản lý thị trường, công tác kỹ thuật trong công nghiệp, trang bị hiệu chuẩn cấp dưới, nghiên cứu và phát triển công nghiệp, nghiên cứu học thuật, chuẩn đầu công nghiệp và phòng thí nghiệm hiệu chuẩn, phòng thí nghiệm chuẩn quốc gia và BIPM, tất cả thông tin cần thiết để đánh giá lại phép đo cần có sẵn cho những người có thể có nhu cầu. Khác biệt đầu tiên là ở thứ bậc thấp hơn của dãy thứ bậc, có nhiều thông tin quan trọng hơn có thể được chuẩn bị sẵn ở dạng báo cáo hiệu chuẩn và hệ thống thử nghiệm được công bố, quy định kỹ thuật thử nghiệm, giấy chứng nhận hiệu chuẩn và thử nghiệm, sổ tay hướng dẫn, tiêu chuẩn quốc tế, tiêu chuẩn quốc gia và quy định địa phương.
7.1.2. Khi các chi tiết của phép đo, bao gồm cách đánh giá độ không đảm bảo của kết quả, được đưa ra bằng cách viện dẫn tới văn bản đã công bố, thường là trường hợp mà kết quả hiệu chuẩn được báo cáo trong giấy chứng nhận, đòi hỏi các công bố này cần được cập nhật để chúng phù hợp với thủ tục đo trong việc sử dụng thực tế.
7.1.3. Nhiều phép đo được tiến hành hàng ngày trong công nghiệp và thương mại mà không có báo cáo rõ ràng về độ không đảm bảo. Tuy nhiên, nhiều phép đo được thực hiện với phương tiện đo được hiệu chuẩn định kỳ hoặc thanh tra. Nếu biết phương tiện đo đáp ứng các quy định kỹ thuật hoặc các văn bản pháp quy hiện hành được áp dụng thì độ không đảm bảo của các số chỉ có thể được suy ra từ các quy định kỹ thuật hoặc từ các văn bản pháp quy.
7.1.4. Mặc dù trong thực tế lượng thông tin cần thiết để lập thành văn bản kết quả đo phụ thuộc vào mục đích sử dụng dự kiến của nó nhưng nguyên tắc cơ bản được yêu cầu phải giữ nguyên không thay đổi; khi báo cáo kết quả đo và độ không đảm bảo của nó, ưu tiên sai theo hướng cung cấp quá nhiều thông tin hơn là quá ít thông tin. Ví dụ, cần:
a) mô tả rõ ràng các phương pháp được sử dụng để tính toán kết quả đo và độ không đảm bảo từ các quan trắc thực nghiệm và dữ liệu đầu vào;
b) liệt kê tất cả các thành phần độ không đảm bảo và lập văn bản đầy đủ cách thức đánh giá chúng;
c) trình bày việc phân tích dữ liệu theo hướng có thể dễ dàng tuân thủ mỗi bước quan trọng và việc tính toán kết quả được báo cáo có thể được lặp lại độc lập nếu cần thiết;
d) đưa ra tất cả sự hiệu chính và hằng số được sử dụng trong phân tích và nguồn của chúng.
7.2. Hướng dẫn cụ thể
7.2.1. Khi lập báo cáo kết quả đo và khi thước đo độ không đảm bảo là độ không đảm bảo chuẩn tổng hợp uc(y) thì cần:
a) đưa ra mô tả đầy đủ về cách xác định đại lượng đo Y;
b) đưa ra ước lượng y của đại lượng đo Y và độ không đảm bảo chuẩn tổng hợp uc(y); đơn vị của y và uc(y) cần luôn được đưa ra;
c) tính đến độ không đảm bảo chuẩn tổng hợp tương đối uc(y)/|y|, |y| # 0, khi thích hợp;
d) đưa ra thông tin được phác thảo trong 7.2.7 hoặc viện dẫn tới tài liệu đã công bố có chứa thông tin.
Nếu thấy có ích đối với người sử dụng kết quả đo dự kiến, ví dụ, để hỗ trợ tính toán sau này cho hệ số phủ hoặc giúp hiểu phép đo thì có thể chỉ ra:
– bậc tự do hiệu dụng ước lượng veff (xem G.4);
– độ không đảm bảo chuẩn tổng hợp Loại A và Loại B ucA(y) và ucB(y) và bậc tử đo hiệu dụng ước lượng của chúng veffA và veffB (xem G.4.1, Chú thích 3).
7.2.2. Khi thước đo độ không đảm bảo là uc(y), ưu tiên trình bày kết quả đo bằng số theo một trong bốn cách sau đây để tránh hiểu nhầm. (Đại lượng có giá trị được báo cáo được giả định là chuẩn khối lượng 100g danh nghĩa ms; các chữ trong ngoặc đơn có thể được bỏ qua cho ngắn gọn nếu uc được định nghĩa ở chỗ khác trong văn bản báo cáo kết quả).
1) “ms = 100,021 47 g với độ không đảm bảo chuẩn tổng hợp) uc = 0,35 mg.”
2) “ms = 100,021 47 (35) g, trong đó số trong ngoặc đơn là trị số của uc( độ không đảm bảo chuẩn tổng hợp) viện dẫn đến các chữ số cuối tương ứng của kết quả trích dẫn.”
3) “ms = 100,021 47 (0,000 35) g, trong đó số trong ngoặc đơn là trị số của uc (độ không đảm bảo chuẩn tổng hợp) trình bày theo đơn vị của kết quả trích dẫn.”
4) “ms = (100,021 47 ± 0,000 35) g, trong đó số nằm sau dấu ± là trị số của uc (độ không đảm bảo chuẩn tổng hợp) và không phải là khoảng tin cậy.”
CHÚ THÍCH: Cần tránh dạng thức ± bất kỳ khi có thể vì nó thường được sử dụng theo truyền thống để ấn định khoảng tương ứng với mức tin cậy cao và do đó có thể bị hiểu nhầm với độ không đảm bảo mở rộng (xem 7.2.4). Ngoài ra, mặc dù mục đích của lời cảnh báo ở điểm 4) là để tránh sự hiểu nhầm này, viết Y = y ± uc(y) vẫn có thể bị hiểu nhầm là hàm ý, đặc biệt nếu lời cảnh báo bị bỏ qua ngẫu nhiên, về độ không đảm bảo mở rộng với k = 1 được mong đợi và khoảng y – uc(y) £ Y £ y + uc(y) có mức tin cậy quy định p, cụ thể là, được kèm theo phân bố chuẩn (xem G.1.3). Như được trình bày trong 6.3.2 và Phụ lục G, giải thích uc(y) theo cách này thường khó chứng minh.
7.2.3. Khi lập báo cáo kết quả đo và khi thước đo độ không đảm bảo là độ không đảm bảo mở rộng U = kuc(y) thì cần:
a) mô tả đầy đủ về cách xác định đại lượng đo Y;
b) tuyên bố kết quả đo là Y = y ± U và đưa ra đơn vị của y và U;
c) tính đến độ không đảm bảo mở rộng tương đối U/|y|, |y| # 0, khi thích hợp;
d) đưa ra giá trị của k sử dụng để thu được U [hoặc, để thuận tiện cho người sử dụng kết quả, đưa ra cả k và uc(y)];
e) đưa ra mức tin cậy gần đúng kèm theo khoảng y ± U và công bố cách xác định;
f) đưa ra thông tin được nêu trong 7.2.7 hoặc viện dẫn đến tài liệu xuất bản có chứa thông tin đó.
7.2.4. Khi thước đo độ không đảm bảo là U, để rõ ràng tối đa, thích hợp hơn là nên trình bày kết quả đo bằng số như trong ví dụ dưới đây. (Các chữ trong dấu ngoặc đơn có thể được bỏ qua cho ngắn gọn nếu U, uc và k được định nghĩa ở chỗ khác trong văn bản báo cáo kết quả)
“ms = (100,021 47 ± 0,000 79) g, khi số nằm sau dấu ± là trị số (độ không đảm bảo mở rộng) U = kuc, với U được xác định từ (độ không đảm bảo chuẩn tổng hợp) uc = 0,35 mg và (hệ số phủ) k = 2,26 dựa trên phân bố t đối với v = 9 bậc tự do và xác định khoảng được ước lượng để có mức tin cậy 95%.”
7.2.5. Nếu phép đo xác định đồng thời nhiều hơn một đại lượng đo, nghĩa là, nếu nó cung cấp hai hoặc nhiều ước lượng đầu ra yi( xem H.2, H.3 và H.4), thì, ngoài việc đưa ra yi và uc(yi), cần đưa ra các phần tử ma trận hiệp phương sai u(yi,yj) hoặc các phần tử r(yi,yj) của ma trận hệ số tương quan (C.3.6, Chú thích 2) (và tốt nhất là cả hai).
7.2.6. Trị số của ước lượng y và độ không đảm bảo chuẩn của nó uc(y) hoặc độ không đảm bảo mở rộng U không nên có số các chữ số nhiều hơn. Thường đủ để trích dẫn uc(y) và U [cũng như độ không đảm bảo chuẩn u(xi) của ước lượng đầu vào xi] có nhiều nhất hai chữ số có nghĩa, mặc dù trong một số trường hợp có thể cần giữ thêm các chữ số bổ sung để tránh sai số làm tròn trong phép tính tiếp theo.
Khi báo cáo kết quả cuối cùng, đôi khi có thể thích hợp làm tròn độ không đảm bảo lên chữ số gần nhất. Ví dụ, uc(y) = 10,47mW có thể được làm tròn lên thành 11 mW. Tuy nhiên, theo ý nghĩa chung cần phổ biến và giá trị như u(xi) = 28,05 kHz cần được làm tròn xuống là 28 kHz. Các ước lượng đầu ra và đầu vào cần được làm tròn phù hợp với độ không đảm bảo của chúng; ví dụ, nếu y = 10,057 62 W với uc(y) = 27 mW thì y cần được làm tròn thành 10,058W. Hệ số tương quan cần được đưa ra với độ chính xác ba con số nếu giá trị tuyệt đối là xấp xỉ một.
7.2.7. Trong báo cáo chi tiết mô tả cách thu được kết quả đo và độ không đảm bảo, cần tuân theo các khuyến nghị của 7.1.4 và do đó:
a) cung cấp giá trị của từng ước lượng đầu vào xi và độ không đảm bảo chuẩn u(xi) cùng với mô tả cách thu được chúng.
b) cung cấp hiệp phương sai ước lượng hoặc hệ số tương quan ước lượng (tốt nhất là cả hai) kèm theo tất cả ước lượng đầu vào có tương quan và phương pháp sử dụng để thu được chúng;
c) cung cấp bậc tự do đối với độ không đảm bảo chuẩn của từng ước lượng đầu vào và cách thu được chúng;
d) cung cấp quan hệ hàm số Y = f(X1, X2, …, XN) và, khi chúng được cho là có ích, đạo hàm riêng hoặc hệ số độ nhạy ![]() /
/![]() . Tuy nhiên, cần đưa ra mọi hệ số như trên được xác định bằng thực nghiệm.
. Tuy nhiên, cần đưa ra mọi hệ số như trên được xác định bằng thực nghiệm.
CHÚ THÍCH: Vì mối quan hệ hàm số f có thể vô cùng phức tạp hoặc có thể không tồn tại rõ ràng mà chỉ như chương trình máy tính, không phải luôn có thể đưa ra f và đạo hàm của nó. Hàm f khi đó có thể được mô tả theo cách chung hoặc chương trình được sử dụng có thể được trích dẫn bằng việc viện dẫn phù hợp. Trong trường hợp đó, quan trọng là làm rõ cách thu được ước lượng y của đại lượng đo Y và độ không đảm bảo chuẩn tổng hợp uc(y)
8. Tóm tắt thủ tục đánh giá và trình bày độ không đảm bảo
Các bước được tuân theo để đánh giá và trình bày độ không đảm bảo của kết quả đo như được trình bày trong tiêu chuẩn này có thể được tóm tắt như sau:
1) Biểu thức toán học mối quan hệ giữa đại lượng đo Y và các đại lượng đầu vào Xi mà Y phụ thuộc: Y = f(X1, X2,…, XN). Hàm f cần chứa mọi đại lượng, bao gồm tất cả các hiệu chính và thừa số hiệu chính, có thể đóng góp thành phần độ không đảm bảo có ý nghĩa vào kết quả đo (xem 4.1.1 và 4.1.2).
2) Xác định xi, giá trị ước lượng của đại lượng đầu vào Xi, trên cơ sở phân tích thống kê các dãy quan trắc hoặc bằng các phương pháp khác (xem 4.1.3).
3) Đánh giá độ không đảm bảo chuẩn u(xi) của từng ước lượng đầu vào xi. Đối với đại lượng đầu vào thu được từ phân tích thống kê các dãy quan trắc, độ không đảm bảo chuẩn được đánh giá như thu được từ phân tích thống kê các dãy quan trắc, độ không đảm bảo chuẩn được đánh giá như mô tả trong 4.2 (đánh giá độ không đảm bảo chuẩn Loại A). Đối với ước lượng đầu vào thu được bằng phương pháp khác, độ không đảm bảo chuẩn u(xi) được đánh giá như mô tả trong 4.3 (đánh giá độ không đảm bảo chuẩn Loại B).
4) Đánh giá hiệp phương sai kèm theo các ước lượng đầu vào có tương quan (xem 5.2).
5) Tính toán kết quả đo, đó là, ước lượng y của đại lượng đo Y, từ mối quan hệ hàm số f sử dụng cho ước lượng xi của đại lượng đầu vào Xi thu được từ bước 2 (xem 4.1.4).
6) Xác định độ không đảm bảo chuẩn tổng hợp uc(y) của kết quả đo y từ độ không đảm bảo chuẩn và hiệp phương sai kèm theo ước lượng đầu vào, như được mô tả trong Điều 5. Nếu phép đo xác định đồng thời nhiều đại lượng đầu ra thì tính hiệp phương sai (xem 7.2.5, H.2, H.3 và H.4).
7) Nếu cần đưa ra độ không đảm bảo mở rộng U, mục đích của nó là cung cấp khoảng y – U đến y + U có thể được kỳ vọng chứa phần lớn phân bố các giá trị có thể quy cho đại lượng đo Y một cách hợp lý, nhân độ không đảm bảo chuẩn tổng hợp uc(y) với hệ số phủ k, thường trong khoảng 2 đến 3, để có được U = kuc(y). Lựa chọn k trên cơ sở mức tin cậy yêu cầu của khoảng trên (xem 6.2, 6.3 và đặc biệt Phụ lục G, thảo luận về sự lựa chọn giá trị k, tạo ra khoảng có mức tin cậy gần với giá trị quy định).
8) Báo cáo kết quả đo y cùng với độ không đảm bảo chuẩn tổng hợp uc(y) hoặc độ không đảm bảo mở rộng U như thảo luận trong 7.2.1 và 7.2.3; sử dụng một trong các mô hình khuyến nghị trong 7.2.2 và 7.2.4. Mô tả cách thu được y và uc(y) hoặc U, như được nêu trong Điều 7.
PHỤ LỤC A
(tham khảo)
KHUYẾN NGHỊ CỦA NHÓM CÔNG TÁC VÀ CIPM
A.1. Khuyến nghị INC-1 (1980)
Nội dung của Khuyến nghị INC-1 (1980) được trình bày trong 0.7 của tiêu chuẩn này.
A.2. Khuyến nghị 1 (CI-1981)
CIPM đã xem xét báo cáo được đệ trình bởi Nhóm công tác về Trình bày độ không đảm bảo và đã thông qua các khuyến nghị sau ở cuộc họp lần thứ 70 được tổ chức vào tháng mười năm 1081 [3]:
Khuyến nghị 1 (CI-1981)
Trình bày độ không đảm bảo thực nghiệm
Ủy ban cân, đo quốc tế
xem xét
– sự cần thiết tìm ra cách thống nhất trình bày độ không đảm bảo đo trong đo lường,
– sự nỗ lực của nhiều tổ chức trong nhiều năm dành cho việc này,
– sự tiến triển đáng khích lệ trong việc tìm giải pháp được chấp nhận, thu được từ các cuộc thảo luận của Nhóm công tác về Trình bày độ không đảm bảo tại BIPM năm 1980,
thừa nhận
– đề xuất của Nhóm công tác có thể lập thành cơ sở của thỏa thuận cuối cùng về trình bày độ không đảm bảo,
khuyến nghị
– đề xuất của Nhóm công tác được phổ biến rộng rãi;
– BIPM cố gắng áp dụng các nguyên tắc trong đó các so sánh quốc tế được thực hiện dưới sự bảo hộ của BIPM trong những năm sắp tới;
– các tổ chức quan tâm khác được khuyến khích xem xét và kiểm chứng các đề xuất này và đưa ra cho BIPM các nhận xét;
– sau hai hoặc ba năm BIPM báo cáo lại về việc áp dụng của các đề xuất này.
A.3. Khuyến nghị 1 (CI-1986)
CIPM đã xem xét thêm vấn đề trình bày độ không đảm bảo ở cuộc họp lần thứ 75 tổ chức vào tháng mười năm 1986 và thông qua khuyến nghị sau đây [4]:
Khuyến nghị 1 (CI-1986)
Việc trình bày độ không đảm bảo trong công tác được tiến hành dưới sự bảo trợ của CIPM.
Ủy ban cân đo quốc tế
xem xét việc Nhóm công tác về Trình bày độ không đảm bảo thông qua Khuyến nghị INC-1 (1980) và việc CIPM thông qua Khuyến nghị 1 (CI-1981).
xem xét thành viên nào đó của Ủy ban Tư vấn mong muốn thông tin chi tiết của Khuyến nghị này cho mục đích công việc thuộc phạm vi hoạt động của họ, đặc biệt đối với so sánh quốc tế.
thừa nhận đoạn 5 của Khuyến nghị INC-1 (1980) liên quan tới các ứng dụng cụ thể, đặc biệt là các ứng dụng có ý nghĩa thương mại, hiện nay đang được xem xét bởi nhóm công tác của Tổ chức Tiêu chuẩn Quốc tế (ISO) chung cho ISO, OIML và IEC, với sự nhất trí và hợp tác của CIPM.
yêu cầu đoạn 5 của Khuyến nghị INC-1 (1980) cần được áp dụng bởi tất cả các bên tham gia khi đưa ra kết quả so sánh quốc tế hoặc công việc khác dưới sự bảo trợ của CIPM và Ủy ban Tư vấn và cần đưa ra độ không đảm bảo tổng hợp của độ không đảm bảo Loại A và Loại B liên quan đến một độ lệch chuẩn.
PHỤ LỤC B
(tham khảo)
THUẬT NGỮ CHUNG VỀ ĐO LƯỜNG
B.1. Nguồn định nghĩa
Định nghĩa của các thuật ngữ đo lường chung liên quan đến tiêu chuẩn này nêu ở đây được lấy từ Từ vựng quốc tế về thuật ngữ chung và cơ bản trong đo lường học (viết tắt là VIM), xuất bản lần hai, 1993 [6], do Tổ chức Tiêu chuẩn Quốc tế (ISO) ban hành, dưới tên của bảy tổ chức hỗ trợ xây dựng và chỉ định chuyên gia soạn thảo tiêu chuẩn: Viện cân đo quốc tế (BIPM), Ủy ban kỹ thuật điện quốc tế (IEC), Liên đoàn quốc tế về hóa học lâm sàng (IFCC), ISO, Liên đoàn quốc tế về hóa học tinh khiết và ứng dụng (IUPAC), Liên đoàn quốc tế về vật lý thuần túy và ứng dụng (IUPAP) và Tổ chức quốc tế về đo lường pháp định (OIML). VIM cần là nguồn đầu tiên tra cứu định nghĩa của các thuật ngữ không có ở đây hoặc trong tài liệu.
CHÚ THÍCH: Một số thuật ngữ và khái niệm cơ bản về thống kê được nêu trong Phụ lục C, trong khi thuật ngữ “giá trị thực”, “sai số” và “độ không đảm bảo” được thảo luận chi tiết hơn trong Phụ lục D.
B.2. Định nghĩa
Như trong Điều 0, trong các định nghĩa sau đây, việc sử dụng dấu ngoặc đơn cho một số từ của một số thuật ngữ có nghĩa là các từ đó có thể bỏ qua nếu không có khả năng gây nhầm lẫn.
Thuật ngữ in đậm trong một số chú thích là thuật ngữ đo lường học bổ sung được định nghĩa trong các chú thích đó, rõ ràng hoặc ẩn ý (xem Tài liệu tham khảo [6]).
B.2.1. Đại lượng (đo được) [(measurable quantity)]
Thuộc tính của hiện tượng, vật hoặc chất có thể phân biệt định tính và xác định định lượng.
CHÚ THÍCH 1: Thuật ngữ đại lượng có thể quy cho đại lượng theo giác quan chung (xem Ví dụ 1) hoặc đại lượng cụ thể (xem Ví dụ 2).
VÍ DỤ 1: Đại lượng theo giác quan chung: chiều dài, thời gian, khối lượng, nhiệt độ, điện trở, nồng độ lượng chất.
VÍ DỤ 2: Đại lượng cụ thể:
– độ dài của thanh cho trước;
– điện trở của mẫu dây kim loại cho trước;
– nồng độ lượng chất của etanol trong mẫu rượu vang cho trước.
CHÚ THÍCH 2: Đại lượng có thể được sắp xếp theo thứ tự độ lớn so với đại lượng khác được gọi là đại lượng cùng loại.
CHÚ THÍCH 3: Đại lượng cùng loại có thể được nhóm lại cùng nhau thành loại đại lượng, ví dụ:
– công, nhiệt, năng lượng;
– độ dày, chu vi, bước sóng.
CHÚ THÍCH 4: Ký hiệu đại lượng được nêu trong TCVN 6398 (ISO 31)1)
[VIM: 19932), định nghĩa 1.1]
B.2.2. Giá trị (của đại lượng) [value (of a quantity)]
Độ lớn của đại lượng cụ thể được trình bày chung bằng đơn vị của phép đo nhân với một số.
VÍ DỤ 1: Độ dài của thanh: 5,34 m hoặc 534 cm.
VÍ DỤ 2: Khối lượng của vật 0,152 kg hoặc 152 g.
VÍ DỤ 3: Nồng độ lượng chất của mẫu nước (H2O): 0,012 mol hoặc 12 mmol.
CHÚ THÍCH 1: Giá trị của đại lượng có thể dương, âm hoặc bằng “không”
CHÚ THÍCH 2: Giá trị của đại lượng có thể được trình bày bằng nhiều cách.
CHÚ THÍCH 3: Giá trị của đại lượng thứ nguyên một thường được trình bày như số thuần túy.
CHÚ THÍCH 4: Đại lượng không thể được thể hiện bằng đơn vị của phép đo nhân với một số có thể được trình bày bằng cách viện dẫn tới thang quy chiếu quy ước hoặc tới thủ tục đo hoặc cả hai.
[VIM: 1993, định nghĩa 1.18]
B.2.3. Giá trị thực (của đại lượng) [true value (of a quantity)]
Giá trị phù hợp với định nghĩa của đại lượng cụ thể đã cho.
CHÚ THÍCH 1: Đây là giá trị có thể thu được bằng phép đo đúng.
CHÚ THÍCH 2: Giá trị thực là bất định.
[VIM: 1993, định nghĩa 1.19]
Bình luận: Xem Phụ lục D, cụ thể là D.3.5 về lý do tại sao thuật ngữ “giá trị thực” không được sử dụng trong tiêu chuẩn này và tại sao thuật ngữ “giá trị thực của đại lượng đo” (hoặc của một đại lượng) và “giá trị của đại lượng đo” (hoặc của đại lượng) được coi là tương đương.
B.2.4. Giá trị thực quy ước (của đại lượng) [conventional true value (of a quantity)]
Giá trị quy cho đại lượng cụ thể và được chấp nhận, đôi khi theo quy ước, là có độ không đảm bảo phù hợp với một mục đích đã cho.
VÍ DỤ 1: Ở địa điểm đã cho, giá trị được ấn định cho đại lượng thể hiện bằng chuẩn chính có thể được xem là giá trị thực quy ước.
VÍ DỤ 2: CODATA (1986) khuyến nghị giá trị đối với hằng số Avogadro: 6,022 136 7 x 1023 mol-1.
CHÚ THÍCH 1: “Giá trị thực quy ước” đôi khi được gọi là giá trị ấn định, ước lượng tốt nhất của giá trị, giá trị quy ước hoặc giá trị quy chiếu. “Giá trị quy chiếu”, theo ý nghĩa này, không nên nhầm lẫn với “giá trị quy chiếu” theo ý nghĩa được sử dụng trong Chú thích của VIM: 1993, định nghĩa 5.7.
CHÚ THÍCH 2: Thông thường, một số kết quả đo đại lượng được sử dụng để thiết lập giá trị thực quy ước.
[VIM: 1993, định nghĩa 1.20]
Bình luận: Xem Bình luận của B.2.3.
B.2.5. Phép đo (measurement)
Tập hợp các thao tác có đối tượng xác định là giá trị của đại lượng.
CHÚ THÍCH; Các thao tác này có thể được thực hiện tự động.
[VIM: 1993, định nghĩa 2.1]
B.2.6. Nguyên lý đo (principle of measurement)
Cơ sở khoa học của phép đo.
VÍ DỤ 1: Hiệu ứng nhiệt điện áp dụng cho phép đo nhiệt độ.
VÍ DỤ 2: Hiệu ứng Josephson áp dụng cho phép đo hiệu điện thế.
VÍ DỤ 3: Hiệu ứng Dophler áp dụng cho phép đo vận tốc.
VÍ DỤ 4: Hiệu ứng Raman áp dụng cho phép đo số sóng của dao động phân tử.
[VIM: 1993, định nghĩa 2.3]
B.2.7. Phương pháp đo (method of measurement)
Chuỗi các thao tác hợp lý, mô tả chung, được sử dụng khi thực hiện phép đo.
CHÚ THÍCH: Có thể phân loại phương pháp đo theo những cách khác nhau như:
– phương pháp thế,
– phương pháp vi sai,
– phương pháp chỉ không.
[VIM: 1993, định nghĩa 2.4]
B.2.8. Thủ tục đo (measurement procedure)
Chuỗi các thao tác, mô tả cụ thể, được sử dụng khi thực hiện phép đo cụ thể theo phương pháp đã cho.
CHÚ THÍCH: Thủ tục đo thường được ghi trong tài liệu đôi khi được gọi là “thủ tục đo” (hoặc phương pháp đo) và thường đủ chi tiết cho phép người vận hành thực hiện phép đo mà không cần thêm thông tin.
[VIM: 1993, định nghĩa 2.5]
B.2.9. Đại lượng đo (measurand)
Đại lượng cụ thể được đo.
VÍ DỤ: Áp suất hơi của mẫu nước đã cho ở 200C.
CHÚ THÍCH; Quy định kỹ thuật của đại lượng đo có thể yêu cầu tuyên bố về các đại lượng như thời gian, nhiệt độ và áp suất.
[VIM: 1993, định nghĩa 2.6]
B.2.10. Đại lượng ảnh hưởng (influence quantity)
Đại lượng không phải là đại lượng đo nhưng ảnh hưởng đến kết quả đo.
VÍ DỤ 1: Nhiệt độ của panme dùng để đo độ dài.
VÍ DỤ 2: Tần số trong phép đo biên độ của hiệu điện thế xoay chiều.
VÍ DỤ 3: Nồng độ sắc tố da cam trong phép đo nồng độ hemoglobin trong mẫu huyết tương máu người.
[VIM: 1993, định nghĩa 2.7]
Bình luận: Định nghĩa về đại lượng ảnh hưởng được hiểu bao gồm các giá trị gắn với chuẩn đo lường, mẫu chuẩn và số liệu tra cứu mà kết quả đo có thể phụ thuộc vào đó, cũng như hiện tượng như sự thay đổi bất thường của phương tiện đo ngắn hạn và các đại lượng như nhiệt độ môi trường, áp suất khí quyển và độ ẩm không khí.
B.2.11. Kết quả đo (result of a measurement)
Giá trị quy cho đại lượng đo, thu được nhờ phép đo.
CHÚ THÍCH 1: Khi đưa ra kết quả cần làm rõ nó có liên quan với:
– số chỉ,
– kết quả chưa hiệu chính,
– kết quả đã hiệu chính.
Và một số kết quả có được tính trung bình hay không.
CHÚ THÍCH 2: Bản tóm tắt kết quả đo đầy đủ bao gồm thông tin về độ không đảm bảo của phép đo.
[VIM:1993, định nghĩa 3.1]
B.2.12. Kết quả chưa hiệu chính (uncorrected result)
Kết quả đo trước khi hiệu chính sai số hệ thống.
[VIM:1993, định nghĩa 3.3]
B.2.13. Kết quả đã hiệu chính (corrected result)
Kết quả đo sau khi hiệu chính sai số hệ thống.
[VIM:1993, định nghĩa 3.4]
B.2.14. Độ chính xác của phép đo (accuracy of measurement)
Mức độ gần nhau theo thỏa thuận giữa kết quả của phép đo và giá trị thực của đại lượng đo.
CHÚ THÍCH 1: “Độ chính xác” là khái niệm định tính.
CHÚ THÍCH 2: Thuật ngữ độ chụm không nên dùng cho “độ chính xác”.
[VIM:1993, định nghĩa 3.5]
Bình luận: Xem Bình luận của B.2.3.
B.2.15. Độ lặp lại (của kết quả đo) [repeatabilty (of results of measurements)]
Mức độ gần nhau theo thỏa thuận giữa các kết quả đo liên tiếp cùng đại lượng đo được tiến hành trong cùng điều kiện đo.
CHÚ THÍCH 1: Các điều kiện này được gọi là điều kiện lặp lại.
CHÚ THÍCH 2: Điều kiện lặp lại bao gồm:
– cùng thủ tục đo,
– cùng người quan trắc,
– cùng phương tiện đo, sử dụng trong cùng điều kiện,
– cùng địa điểm,
– lặp lại trong một khoảng thời gian ngắn.
CHÚ THÍCH 3: Độ lặp lại có thể được thể hiện định lượng theo đặc điểm phân tán của các kết quả.
[VIM:1993, định nghĩa 3.6]
B.2.16. Độ tái lập (của kết quả đo) [reproducibility (of results of measurements)]
Mức độ gần nhau theo thỏa thuận giữa các kết quả đo cho cùng đại lượng đo được tiến hành dưới điều kiện thay đổi cho phép đo.
CHÚ THÍCH 1: Biểu thức hợp lý độ tái lập yêu cầu các quy định kỹ thuật về điều kiện thay đổi.
CHÚ THÍCH 2: Điều kiện thay đổi bao gồm:
– nguyên lý đo,
– phương pháp đo,
– người quan trắc,
– phương tiện đo,
– chuẩn chính,
– địa điểm,
– điều kiện sử dụng,
– thời gian.
CHÚ THÍCH 3: Độ tái lập có thể được thể hiện định lượng theo đặc điểm phân tán của kết quả.
CHÚ THÍCH 4: Kết quả ở đây thường được hiểu là kết quả đã hiệu chính.
[VIM:1993, định nghĩa 3.7]
B.2.17. Độ lệch chuẩn thực nghiệm (experimental standard deviation)
Đối với dãy n phép đo của cùng đại lượng đo, đại lượng s(qb) đặc trưng cho sự phân tán kết quả và được cho bằng công thức:
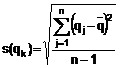
qk là kết quả đo thứ k và q là trung bình cộng của n kết quả được xem xét.
CHÚ THÍCH 1: Coi loạt n giá trị là mẫu phân bố, ![]() là ước lượng không lệch của trung bình mq và s2(qk) là ước lượng không chệch của phương sai s2, của phân bố đó.
là ước lượng không lệch của trung bình mq và s2(qk) là ước lượng không chệch của phương sai s2, của phân bố đó.
CHÚ THÍCH 2: Biểu thức s(qk)/![]() là ước lượng về độ lệch chuẩn của phân bố q và được gọi là độ lệch chuẩn thực nghiệm của trung bình.
là ước lượng về độ lệch chuẩn của phân bố q và được gọi là độ lệch chuẩn thực nghiệm của trung bình.
CHÚ THÍCH 3: “Độ lệch chuẩn thực nghiệm của trung bình” đôi khi được gọi không chính xác là sai số chuẩn của trung bình.
CHÚ THÍCH 4: Lấy từ VIM:1993, định nghĩa 3.8.
Bình luận: Một số ký hiệu được sử dụng trong VIM đã được thay đổi để đạt được sự nhất quán với ký hiệu được sử dụng trong 4.2 của tiêu chuẩn này.
B.2.18. Độ không đảm bảo (của phép đo) [uncertainty (of measurement)]
Tham số, kèm theo kết quả đo, đặc trưng cho sự phân tán của các giá trị có thể được quy thích hợp cho đại lượng đo một cách hợp lý.
CHÚ THÍCH 1: Tham số có thể là, ví dụ, độ lệch chuẩn (hoặc bội số đã cho của nó) hoặc nửa độ rộng của khoảng có mức tin cậy quy định.
CHÚ THÍCH 2: Thông thường, độ không đảm bảo của phép đo bao gồm nhiều thành phần. Một số trong các thành phần này có thể được đánh giá từ phân bố thống kê kết quả của các dãy phép đo và có thể được đặc trưng bằng độ lệch chuẩn thực nghiệm. Các thành phần khác, cũng có thể được đặc trưng bằng độ lệch chuẩn, được đánh giá từ phân bố xác suất giả định dựa trên cơ sở kinh nghiệm hoặc thông tin khác.
CHÚ THÍCH 3: Kết quả đo được hiểu là ước lượng tốt nhất giá trị của đại lượng đo và tất cả các thành phần của độ không đảm bảo, bao gồm thành phần xuất hiện từ ảnh hưởng hệ thống, như các thành phần kèm theo sự hiểu chính và chuẩn chính, góp phần vào sự phân tán.
[VIM:1993, định nghĩa 3.9]
Bình luận: Theo VIM, định nghĩa này và các chú thích giống như trong tiêu chuẩn này (xem 2.2.3).
B.2.19. Sai số (của phép đo) [error (of measurement)]
Kết quả đo trừ đi giá trị thực của đại lượng đo.
CHÚ THÍCH 1: Vì giá trị thực không thể xác định được nên trong thực tế sử dụng giá trị thực quy ước [xem VIM:1993, định nghĩa 1.19 (B.2.3) và 1.20 (B.2.4)].
CHÚ THÍCH 2: Khi cần phân biệt “sai số” với “sai số tương đối”, khái niệm “sai số” đôi khi được gọi là sai số tuyệt đối của phép đo. Không nên nhầm lẫn với giá trị tuyệt đối của sai số, là mô đun của sai số.
[VIM:1993, định nghĩa 3.10]
Bình luận: Nếu kết quả đo phụ thuộc vào giá trị các đại lượng không phải đại lượng đo thì sai số giá trị đo được của các đại lượng này góp phần vào sai số của kết quả đo. Xem thêm Bình luận của B.2.22 và B.2.3.
B.2.20. Sai số tương đối (relative error)
Sai số của phép đo chia cho giá trị thực của đại lượng đo.
CHÚ THÍCH: Vì giá trị thực không thể xác định được nên trong thực tế sử dụng giá trị thực quy ước [xem VIM:1993, định nghĩa 1.19 (B.2.3) và 1.20 (B.2.4)]
[VIM:1993, định nghĩa 3.12)]
Bình luận: Xem Bình luận của B.2.3.
B.2.21. Sai số ngẫu nhiên (random error)
Kết quả đo trừ đi trung bình thu được từ một số vô hạn các phép đo của cùng đại lượng đo được thực hiện dưới điều kiện lặp lại.
CHÚ THÍCH 1: Sai số ngẫu nhiên bằng sai số đo trừ đi sai số hệ thống.
CHÚ THÍCH 2: Vì chỉ có thể thực hiện số phép đo có hạn nên có thể chỉ xác định được ước lượng của sai số ngẫu nhiên.
[VIM:1993, định nghĩa 3.13]
Bình luận: Xem Bình luận của B.2.22.
B.2.22. Sai số hệ thống (systematic error)
Trung bình nhận được từ số phép đo có hạn của cùng đại lượng đo được thực hiện dưới điều kiện lặp lại trừ đi giá trị thực của đại lượng đo.
CHÚ THÍCH 1: Sai số hệ thống bằng sai số đo trừ đi sai số ngẫu nhiên.
CHÚ THÍCH 2: Giống như giá trị thực, không thể biết chính xác sai số hệ thống và nguyên nhân của nó.
CHÚ THÍCH 3: Với phương tiện đó, xem “độ chệch” (VIM:1993, định nghĩa 5.25)
[VIM:1993, định nghĩa 3.14]
Bình luận: Sai số kết quả đo (xem B.2.19) thường có thể được coi là xuất hiện từ một số ảnh hưởng ngẫu nhiên và hệ thống đóng góp các thành phần sai số riêng lẻ vào sai số của kết quả. Xem thêm Bình luận của B.2.19 và B.2.3.
B.2.23. Hiệu chính (correction)
Giá trị được bổ sung theo phương pháp đại số vào kết quả chưa được hiệu chính của phép đo để bù cho sai số hệ thống.
CHÚ THÍCH 1: Hiệu chính bằng giá trị âm của sai số hệ thống được ước lượng.
CHÚ THÍCH 2: Vì không thể biết được đầy đủ sai số hệ thống nên việc bù không thể hoàn toàn.
[VIM:1993, định nghĩa 3.15]
B.2.24. Thừa số hiệu chính (correction factor)
Thừa số được nhân với kết quả đo chưa được hiệu chính của phép đo để bù cho sai số hệ thống.
CHÚ THÍCH: Vì không thể biết được đầy đủ sai số hệ thống nên việc bù không thể hoàn toàn.
[VIM:1993, định nghĩa 3.16]
PHỤ LỤC C
(tham khảo)
THUẬT NGỮ VÀ KHÁI NIỆM THỐNG KÊ CƠ BẢN
C.1. Nguồn định nghĩa
Định nghĩa của các thuật ngữ thống kê cơ bản cho trong phụ lục này được lấy từ tiêu chuẩn ISO 3534-1:1993* [7]. Đây cần là nguồn tra cứu đầu tiên cho định nghĩa của các thuật ngữ không có ở đây. Để tạo thuận lợi cho việc sử dụng tiêu chuẩn này, một số trong các thuật ngữ này và khái niệm cơ bản của chúng được nêu chi tiết trong C.3 sau phần trình bày định nghĩa chính thức của chúng ở C.2. Tuy nhiên, C.3 cũng bao gồm các định nghĩa của một số thuật ngữ liên quan, không căn cứ trực tiếp vào ISO 3534-1:1993.
C.2. Định nghĩa
Như trong Điều 0 và Phụ lục B, việc sử dụng dấu ngoặc đơn cho các từ nào đó nghĩa là các từ này có thể được bỏ qua nếu điều này không gây nhầm lẫn.
Các thuật ngữ từ C.2.1 đến C.2.14 được định nghĩa theo tính chất của tổng thể. Định nghĩa của các thuật ngữ từ C.2.15 đến C.2.31 liên quan đến tập hợp các quan trắc (xem tài liệu tham khảo [7]).
C.2.1. Xác suất (probability)
Số thực trong thang từ 0 đến 1 kèm theo biến cố ngẫu nhiên.
CHÚ THÍCH: Nó có thể liên quan đến tần suất xuất hiện tương đối trong một thời gian dài hoặc mức độ tin tưởng vào khả năng xuất hiện biến cố. Đối với mức độ tin tưởng cao, xác suất gần bằng 1.
[ISO 3534-1:1993, định nghĩa 1.1]
C.2.2. Biến ngẫu nhiên (random variable)
Biến (variate)
Biến có thể nhận giá trị bất kỳ của tập hợp các giá trị quy định và với giá trị kèm theo phân bố xác suất [ISO 3534-1:1993, định nghĩa 1.3 (C.2.3)].
CHÚ THÍCH 1: Biến ngẫu nhiên có thể chỉ lấy các giá trị tách biệt được gọi là “rời rạc”. Biến ngẫu nhiên có thể lấy giá trị bất kỳ trong khoảng có hạn hoặc vô hạn được gọi là “liên tục”.
CHÚ THÍCH 2: Xác suất của biến cố A được ký hiệu là Pr(A) hoặc P(A).
[ISO 3534-1:1993, định nghĩa 1.2]
Bình luận: Ký hiệu Pr(A) được sử dụng trong tiêu chuẩn này thay cho Pr(A) được sử dụng trong ISO 3534-1:1993.
C.2.3. Phân bố xác suất (của biến ngẫu nhiên) [probability distribution (of a random variable)]
Hàm đưa ra xác suất mà biến ngẫu nhiên lấy giá trị bất kỳ đã cho hoặc thuộc tập hợp các giá trị đã cho.
CHÚ THÍCH; Xác suất trên toàn bộ tập hợp giá trị của biến ngẫu nhiên bằng 1.
[ISO 3534-1:1993, định nghĩa 1.3]
C.2.4. Hàm phân bố (distribution function)
Hàm đưa ra xác suất, với mỗi giá trị x, mà biến ngẫu nhiên X nhỏ hơn hoặc bằng x:
F(x) = Pr(X £ x)
[ISO 3534-1:1993, định nghĩa 1.4]
C.2.5. Hàm mật độ xác suất (đối với biến ngẫu nhiên liên tục)[probability density function (for a continuous random variable)]
Đạo hàm (nếu có) của hàm phân bố:
f(x) = dF(x)/dx
CHÚ THÍCH; f(x)dx là “phần tử xác suất””
f(x)dx = Pr(x < X < x + dx)
[ISO 3534-1:1993, định nghĩa 1.5]
C.2.6. Hàm khối lượng xác suất (probability mass function)
Hàm đưa ra xác suất, với mỗi giá trị xj của biến ngẫu nhiên rời rạc X, xác suất pi biến ngẫu nhiên bằng xi:
pi = Pr (X = x)
[ISO 3534-1:1993, định nghĩa 1.6]
C.2.7. Tham số (parameter)
Đại lượng được sử dụng trong việc mô tả phân bố xác suất của biến ngẫu nhiên.
[ISO 3534-1:1993, định nghĩa 1.12]
C.2.8. Tương quan (correlation)
Mối quan hệ giữa hai hoặc nhiều biến ngẫu nhiên trong phân bố hai hoặc nhiều biến ngẫu nhiên.
CHÚ THÍCH: Hầu hết thước đo thống kê của tương quan chỉ đo mức độ của quan hệ tuyến tính.
[ISO 3534-1:1993, định nghĩa 1.13]
C.2.9. Kỳ vọng (của biến ngẫu nhiên hoặc của phân bố xác suất) [expectation (of a random variable or of a probability distribution)]
Giá trị kỳ vọng (expected value)
Trung bình (mean)
1) Đối với biến ngẫu nhiên rời rạc X lấy giá trị xi với xác suất pi, thì kỳ vọng, nếu có, bằng:
m = E(X) = ![]()
Tổng được mở rộng cho tất cả các giá trị xi có thể được lầy bởi X.
2) Đối với biến ngẫu nhiên liên tục X có hàm mật độ xác suất f(x), thì kỳ vọng, nếu có, bằng:
m = E(X) = ![]()
[ISO 3534-1:1993, định nghĩa 1.18]
C.2.10. Biến ngẫu nhiên quy tâm (centred random variable)
Biến ngẫu nhiên có kỳ vọng bằng “không”.
CHÚ THÍCH: Nếu biến ngẫu nhiên X có kỳ vọng bằng m thì biến ngẫu nhiên quy tâm tương ứng là (X – m).
[ISO 3534-1:1993, định nghĩa 1.21]
C.2.11. Phương sai (của biến ngẫu nhiên của phân bố xác suất) [variance (of a random variable or of a probability distribution)]
Kỳ vọng của bình phương biến ngẫu nhiên quy tâm [ISO 3534-1:1993, định nghĩa 1.21 (C.2.10)]:
![]()
[ISO 3534-1:1993, định nghĩa 1.22]
C.2.12. Độ lệch chuẩn (của biến ngẫu nhiên hoặc của phân bố xác suất) [standard deviation (of a random variable or of a probability distribution)]
Dương căn bậc hai của phương sai:
![]()
[ISO 3534-1:1993, định nghĩa 1.23]
C.2.13. Mômen* quy tâm bậc q (central moment of order q)
Trong phân bố đơn biến, kỳ vọng của biến ngẫu nhiên quy tâm (X – m) lũy thừa q:
E[(X – m)q]
CHÚ THÍCH: Mômen quy tâm bậc 2 là phương sai [ISO 3534-1:1993, định nghĩa 1.22 (C.2.11)] của biến ngẫu nhiên X.
[ISO 3534-1:1993, định nghĩa 1.28]
C.2.14. Phân bố chuẩn (normal distribution)
Phân bố Laplace-Gauss (Laplace-Gauss distribution)
Phân bố xác suất của biến ngẫu nhiên liên tục X với hàm mật độ xác suất của nó là:
![]()
Với –¥ < x < +¥
CHÚ THÍCH: m là kỳ vọng và s là độ lệch chuẩn của phân bố chuẩn.
[ISO 3534-1:1993, định nghĩa 1.37]
C.2.15. Đặc trưng (characteristic)
Tính chất giúp nhận biết hoặc phân biệt giữa các cá thể trong tổng thể đã cho.
CHÚ THÍCH: Đặc trưng có thể là định lượng (bằng biến) hoặc định tính (bằng thuộc tính).
[ISO 3534-1:1993, định nghĩa 2.2]
C.2.16. Tổng thể (population)
Toàn thể cá thể được xem xét.
CHÚ THÍCH: Trong trường hợp biến ngẫu nhiên, phân bố xác suất [ISO 3534-1:1993, định nghĩa 1.3 (C.2.3)] được xem xét để xác định tổng thể của biến đó.
[ISO 3534-1:1993, định nghĩa 2.3]
C.2.17. Tần suất (frequency)
Số lần xuất hiện của loại biến cố đã cho hoặc số lần quan trắc trong một lớp quy định.
[ISO 3534-1:1993, định nghĩa 2.11]
C.2.18. Phân bố tần suất (frequency distribution)
Mối quan hệ thực nghiệm giữa các giá trị của đặc trưng và tần suất của chúng hoặc tần suất tương đối của chúng.
CHÚ THÍCH: Phân bố cụ thể được trình bày bằng đồ thị như biểu đồ tần suất (ISO 3534-1:1993, định nghĩa 2.17), biểu đồ cột (ISO 3534-1:1993, định nghĩa 1.18), đa giác tần số tích lũy (ISO 3534-1:1993, định nghĩa 2.19) hoặc bảng hai chiều (ISO 3534-1:1993, định nghĩa 2.22).
[ISO 3534-1:1993, định nghĩa 2.15]
C.2.19. Trung bình cộng (arthmetic mean)
Trung bình (average)
Tổng các giá trị chia cho số giá trị.
CHÚ THÍCH 1: Thuật ngữ “trung bình” (mean) được sử dụng chung khi đề cập đến tham số của tổng thể và thuật ngữ “trung bình) average) khi đề cập đến kết quả tính toán số liệu thu được trong mẫu.
CHÚ THÍCH 2: Trung bình (average) của một mẫu ngẫu nhiên đơn giản được lấy từ tổng thể là một ước lượng không chệch của trung bình (mean) của tổng thể này. Tuy nhiên, các ước lượng khác, như trung bình hình học hoặc hàm điều hòa, trung vị hoặc mốt, đôi khi được sử dụng.
[ISO 3534-1:1993, định nghĩa 2.26]
C.2.20. Phương sai (variance)
Thước đo độ phân tán, là tổng bình phương độ lệch của các quan trắc so với trung bình của chúng chia cho số quan trắc trừ một.
VÍ DỤ: Với n quan trắc x1, x2, …, xN với trung bình
![]()
phương sai bằng:
![]()
CHÚ THÍCH 1: Phương sai mẫu là ước lượng không lệch của phương sai tổng thể.
CHÚ THÍCH 2: Phương sai là n/(n-1) lần mômen quy tâm bậc 2 (xem chú thích ISO 3534-1:1993, định nghĩa 2.39).
[ISO 3534-1:1993, định nghĩa 2.23]
Bình luận: Phương sai được định nghĩa ở đây có tên gọi thích hợp hơn “ước lượng mẫu của phương sai tổng thể”. Phương sai của mẫu thường được xác định là mômen quy tâm bậc 2 của mẫu (xem C.2.13 và C.2.22).
C.2.21. Độ lệch chuẩn (standard deviation)
Dương căn bậc hai của phương sai.
VÍ DỤ; Độ lệch chuẩn mẫu là ước lượng chệch của độ lệch chuẩn tổng thể.
[ISO 3534-1:1993, định nghĩa 2.34]
C.2.22. Mômen quy tâm bậc q (central moment of order q)
Trong phân bố của đặc trưng đơn, trung bình cộng lũy thừa q của hiệu giữa các giá trị quan trắc và trung bình x của chúng:
![]()
Trong đó n là số lượng quan trắc.
CHÚ THÍCH: Mômen quy tâm bậc 1 bằng “không”.
[ISO 3534-1:1993, định nghĩa 2.37]
C.2.23. Thống kê (statistic)
Hàm số của các biến ngẫu nhiên của mẫu.
CHÚ THÍCH: Thống kê, như hàm số của các biến ngẫu nhiên, cũng là biến ngẫu nhiên và như vậy nó giả định các giá trị khác nhau giữa các mẫu. Giá trị của thống kê thu được nhờ sử dụng các giá trị quan trắc trong hàm này có thể được sử dụng trong kiểm nghiệm thống kê hoặc như một ước lượng của tham số tổng thể, ví dụ trung bình hoặc độ lệch chuẩn.
[ISO 3534-1:1993, định nghĩa 2.45]
C.2.24. Phép ước lượng (estimation)
Phép tính ấn định, từ các quan trắc trong mẫu, trị số cho các tham số của phân số được chọn làm mô hình thống kê của tổng thể từ đó mẫu này được lấy.
CHÚ THÍCH: Kết quả của phép tính này có thể được thể hiện như một giá trị [ước lượng điểm: xem ISO 3534-1:1993, định nghĩa 2.51 (C.2.26)] hoặc ước lượng khoảng [xem ISO 3534-1:1993, định nghĩa 2.57 (C.2.27) và 2.58 (C.2.28)].
[ISO 3534-1:1993, định nghĩa 2.49]
C.2.25. Hàm ước lượng (estimator)
Thống kê dùng để ước lượng tham số tổng thể.
[ISO 3534-1:1993, định nghĩa 2.50]
C.2.26. Ước lượng (estimate)
Giá trị của hàm ước lượng thu được như kết quả của phép ước lượng.
[ISO 3534-1:1993, định nghĩa 2.51]
C.2.27. Khoảng tin cậy hai phía (two-sided confidence interval)
Khi T1 và T2 là hai hàm giá trị quan trắc sao cho, θ là tham số tổng thể được ước lượng, xác suất Pr(T1 £ θ £T2) ít nhất bằng (1 – a) [trong đó (1 – a) là số cố định, dương và nhỏ hơn 1], khoảng giữa T1 và T2 là khoảng tin cậy (1 – a) hai phía đối với θ.
CHÚ THÍCH 1: Giới hạn T1 và T2 của khoảng tin cậy là các thống kê [ISO 3534-1:1993, định nghĩa 2.45 (C.2.23)] và như thế sẽ thường giả định các giá trị khác nhau cho các mẫu.
CHÚ THÍCH 2: Trong dãy mẫu dài, tần suất tương đương trong trường hợp giá trị thực của tham số tổng thể θ được khoảng tin cậy phủ lớn hơn hoặc bằng (1 – a).
[ISO 3534-1:1993, định nghĩa 2.57]
C.2.28. Khoảng tin cậy một phía (one-sided confidence interval)
Khi T là hàm giá trị quan trắc sao cho, θ là tham số tổng thể được ước lượng, xác suất Pr(T³θ) [hoặc xác suất Pr(T £ θ)] ít nhất bằng (1 – a) là số cố định, dương và nhỏ hơn 1, khoảng từ giá trị dương nhỏ nhất của θ tới T (hoặc khoảng từ T tới giá trị dương lớn nhất của θ) là khoảng tin cậy (1 – a) một phía đối với θ.
CHÚ THÍCH 1: Giới hạn T của khoảng tin cậy là thống kê [ISO 3534-1:1993, định nghĩa 2.45 (C.2.23)] và như thế sẽ thường giả định các giá trị khác nhau cho các mẫu.
CHÚ THÍCH 2: Xem Chú thích 2 của ISO 3534-1:1993, định nghĩa 2.57 (C.2.27).
[ISO 3534-1:1993, định nghĩa 2.58]
C.2.29. Hệ số tin cậy ( confidence coefficient)
Mức tin cậy (confidence level)
Giá trị (1 – a) của xác suất gắn với khoảng tin cậy hoặc khoảng phủ thống kê. [Xem ISO 3534-1:1993, định nghĩa 2.57 (C.2.27), 2.58 (C.2.28) và 2.61 (C.2.30).]
CHÚ THÍCH: (1 – a) thường được thể hiện theo phần trăm.
[ISO 3534-1:1993, định nghĩa 2.59]
C.2.30. Khoảng phủ thống kê (statistical coverage interval)
Khoảng có thể được quy định với mức tin cậy đã cho rằng nó chứa ít nhất một tỷ lệ quy định của tổng thể.
CHÚ THÍCH 1: Khi cả hai giới hạn được xác định bằng thống kê, khoảng đó là hai phía. Khi một trong hai giới hạn không hữu hạn hoặc biến số có biên thì khoảng đó là một phía.
CHÚ THÍCH 2: Kết quả này còn được gọi là “khoảng dung sai thống kê”. Không nên sử dụng thuật ngữ này vì có thể gây nhầm lẫn với “khoảng dung sai” được định nghĩa trong ISO 3534-2:1993.
[ISO 3534-1:1993, định nghĩa 2.61]
C.2.31. Bậc tự do (degrees of freedom)
Nói chung, số các số hạng trong một tổng trừ đi số các ràng buộc đối với các số hạng của tổng đó.
[ISO 3534-1:1993, định nghĩa 2.85]
C.3. Soạn thảo thuật ngữ và khái niệm
C.3.1. Kỳ vọng
Kỳ vọng của hàm g(z) trên hàm mật độ xác suất p(z) của biến ngẫu nhiên z được định nghĩa bằng
![]()
Trong đó, từ định nghĩa của p(z), ![]() = 1. Kỳ vọng của biến ngẫu nhiên z , được ký hiệu là mz, và cũng được gọi là giá trị kỳ vọng hoặc trung bình của z, được cho bởi:
= 1. Kỳ vọng của biến ngẫu nhiên z , được ký hiệu là mz, và cũng được gọi là giá trị kỳ vọng hoặc trung bình của z, được cho bởi:
![]()
Kỳ vọng được ước lượng thống kê bằng ![]() , trung bình cộng hoặc trung bình của n quan trắc độc lập zi của biến ngẫu nhiên z, hàm mật độ xác suất là p(z):
, trung bình cộng hoặc trung bình của n quan trắc độc lập zi của biến ngẫu nhiên z, hàm mật độ xác suất là p(z):
![]()
C.3.2. Phương sai
Phương sai của biến ngẫu nhiên là kỳ vọng của độ lệch toàn phương về kỳ vọng của nó. Do đó phương sai của biến ngẫu nhiên z với hàm mật độ xác suất p(z) được cho bởi:
![]()
Trong đó mz là kỳ vọng của z. Phương sai ![]() có thể được ước lượng bằng:
có thể được ước lượng bằng:
![]()
Trong đó
![]()
Và zi là n quan trắc độc lập của z.
CHÚ THÍCH 1: Thừa số n-1 trong biểu thức tính s2(zi) phát sinh từ mối tương quan giữa zi và ![]() , phản ánh thực tế là chỉ có n-1 cá thể độc lập trong tập hợp {zi –
, phản ánh thực tế là chỉ có n-1 cá thể độc lập trong tập hợp {zi – ![]() }.
}.
CHÚ THÍCH 2: Nếu biết trước kỳ vọng mz của z thì phương sai có thể được ước lượng bằng:
![]()
Phương sai của trung bình cộng hoặc trung bình các quan trắc, không phải phương sai của các quan trắc riêng, là thước đo thích hợp độ không đảm bảo của kết quả đo. Phương sai của biến z cần được phân biệt cẩn thận với phương sai của trung bình ![]() . Phương sai của trung bình cộng của dãy n quan trắc độc lập zi của z được cho bằng s2(
. Phương sai của trung bình cộng của dãy n quan trắc độc lập zi của z được cho bằng s2(![]() ) = s2(zi)/n và được ước lượng bằng phương sai thực nghiệm của trung bình:
) = s2(zi)/n và được ước lượng bằng phương sai thực nghiệm của trung bình:
s2(![]() ) =
) = ![]()
C.3.3. Độ lệch chuẩn
Độ lệch chuẩn là dương căn bậc hai của phương sai. Trong khi độ không đảm bảo chuẩn Loại A thu được bằng cách lấy căn bậc hai của phương sai được đánh giá thống kê, thường thuận tiện hơn khi xác định độ không đảm bảo chuẩn Loại B để đánh giá độ lệch chuẩn tương đương phi thống kê trước, sau đó thu được phương sai tương đương bằng cách lấy bình phương độ lệch chuẩn.
C.3.4. Hiệp phương sai
Hiệp phương sai của hai biến ngẫu nhiên là thước đo sự phụ thuộc lẫn nhau của chúng. Hiệp phương sai của biến ngẫu nhiên y và z được xác định bằng:
cov(y,z) = cov(z,y) = E{[y – E(y)][z – E(z)]}
dẫn tới:
cov(y,z) = cov(z,y)
= 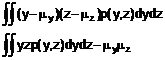
Trong đó p(y,z) là hàm mật độ xác suất chung của hai biến y và z. Hiệp phương sai cov(y,z) [còn được ký hiệu là v(y,z)] có thể được ước lượng bằng s(yi,zi) thu được từ n cặp quan trắc đồng thời độc lập yi và zi của y và z.
s(yi,zi) = ![]()
trong đó
![]()
và
![]()
CHÚ THÍCH: Hiệp phương sai ước lượng của hai trung bình ![]() và
và ![]() được cho bằng s(
được cho bằng s(![]() ,
,![]() ) = s(yi,si)/n.
) = s(yi,si)/n.
C.3.5. Ma trận hiệp phương sai
Với phân bố xác suất đa biến, ma trận V với các phần tử bằng các phương sai và hiệp phương sai của biến được gọi là ma trận hiệp phương sai. Các phần tử đường chéo, v(y,z) º s2(z) hoặc s(zi,zi) º s2(zi), là các phương sai, trong khi các phần thử không thuộc đường chéo, v(y,z) hoặc s(yi,zi) là hiệp phương sai.
C.3.6. Hệ số tương quan
Hệ số tương quan là thước đo sự phụ thuộc lẫn nhau tương đối của hai biến, bằng tỉ số của hiệp phương sai của biến trên dương căn bậc hai của phương sai. Do đó
![]()
với các ước lượng
![]()
Hệ số tương quan đơn thuần là số sao cho -1 £ r £ +1 hoặc -1 £ r(yi,zi) £ +1.
CHÚ THÍCH 1: vì r và r đơn thuần là các số trong dãy và bao gồm cả -1 và +1, trong khi hiệp phương sai thường là đại lượng có kích thước và độ lớn vật lý phức tạp nên hệ số tương quan thường hữu ích hơn hiệp phương sai.
CHÚ THÍCH 2: Với phân bố xác suất đa biến, ma trận hệ số tương quan thường được đưa ra thay cho ma trận hiệp phương sai. Vì r(y,y) = 1 và r(yi,yi) =1 nên các phần tử đường chéo của ma trận này bằng một.
CHÚ THÍCH 3: Nếu các ước lượng đầu vào xi và xj có tương quan (xem 5.2.2) và nếu thay đổi di trong xi dẫn đến thay đổi dj trong xj thì hệ số tương quan gắn với xi và xi được ước lượng xấp xỉ bằng
r(xi,xj) » u(xi)dj/[u(xj)di]
Quan hệ này có thể dùng làm cơ sở ước lượng hệ số tương quan thực nghiệm. Nó cũng có thể được sử dụng để tính sự thay đổi gần đúng trong một ước lượng đầu vào do sự thay đổi trong một ước lượng khác nếu đã biết hệ số tương quan của chúng.
C.3.7. Tính độc lập
Hai biến ngẫu nhiên độc lập về thống kê nếu phân bố xác suất chung của chúng là kết quả của các phân bố xác suất riêng lẻ.
CHÚ THÍCH: Nếu hai biến ngẫu nhiên độc lập thì hiệp phương sai và hệ số tương quan của chúng bằng “không” nhưng trường hợp ngược lại thì không chắc như vậy.
C.3.8. Phân bố t; Phân bố Student
Phân bố t và phân bố Student là phân bố xác suất của biến ngẫu nhiên liên tục t có hàm mật độ xác suất bằng:
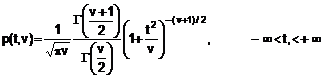
Trong đó G là hàm gamma và v > 0. Kỳ vọng của phân bố t bằng “không” và phương sai của nó là v/(v – 2) với v > 2. Khi v -> ¥, phân bố t tiến gần đến phân bố chuẩn với m = 0 và s = 1 (xem C.2.14).
Phân bố xác suất của biến (![]() – mz)/s(
– mz)/s(![]() ) là phân bố t nếu biến ngẫu nhiên z có phân bố chuẩn với kỳ vọng mz, trong đó
) là phân bố t nếu biến ngẫu nhiên z có phân bố chuẩn với kỳ vọng mz, trong đó ![]() là trung bình cộng của n quan trắc độc lập zi của z, s(zi) là độ lệch chuẩn thực nghiệm của n quan trắc, và s(
là trung bình cộng của n quan trắc độc lập zi của z, s(zi) là độ lệch chuẩn thực nghiệm của n quan trắc, và s(![]() ) = s(zi)/
) = s(zi)/![]() là độ lệch chuẩn thực nghiệm của trung bình
là độ lệch chuẩn thực nghiệm của trung bình ![]() với v = n -1 bậc tự do.
với v = n -1 bậc tự do.
PHỤ LỤC D
(tham khảo)
GIÁ TRỊ “THỰC”, SAI SỐ VÀ ĐỘ KHÔNG ĐẢM BẢO
Thuật ngữ giá trị thực (B.2.3) đã được sử dụng trước đây trong các tài liệu về độ không đảm bảo nhưng không được dùng trong tiêu chuẩn này vì những lý do được trình bày trong phụ lục này. Vì thuật ngữ “đại lượng đo”, “sai số” và “độ không đảm bảo” thường xuyên bị hiểu sai nên phụ lục này cũng cung cấp thêm thông tin về ý tưởng cơ bản của chúng để bổ sung cho thông tin được nêu trong Điều 3. Hai hình được trình bày để minh họa vì sao khái niệm độ không đảm bảo được chấp nhận trong tiêu chuẩn này được dựa trên kết quả đo và độ không đảm bảo được đánh giá của nó mà không dựa trên giá trị “thực” và sai số của đại lượng chưa biết.
D.1. Đại lượng đo
D.1.1. Bước đầu tiên trong việc thực hiện phép đo là xác định đại lượng đo – đại lượng được đo; đại lượng đo không thể được xác định bằng giá trị mà chỉ bằng mô tả đại lượng. Tuy nhiên, về nguyên tắc, đại lượng đo không thể được mô tả đầy đủ mà không có một lượng vô hạn thông tin. Do đó, trong phạm vi có thể giải thích, việc định nghĩa không đầy đủ của đại lượng đo đưa vào trong độ không đảm bảo của kết quả đo thành phần của độ không đảm bảo có thể đáng kể hoặc không đáng kể so với độ chính xác yêu cầu của phép đo.
D.1.2. Thông thường, định nghĩa của đại lượng đo xác định trạng thái vật lý và điều kiện cụ thể.
VÍ DỤ: Vận tốc của âm thanh trong không khí khô của thành phần (phần mol) N2 = 0,780 8, O2 = 0,209 5, Ar = 0,009 35 và CO2 = 0,000 35 ở nhiệt độ T = 273,15 K và áp suất p = 101 325 Pa.
D.2. Đại lượng được thể hiện
D.2.1. Lý tưởng là đại lượng được thể hiện cho phép đo hoàn toàn phù hợp với định nghĩa của đại lượng đo. Tuy nhiên, đại lượng này thường không thể được thể hiện và phép đo thực hiện trên đại lượng là đại lượng xấp xỉ của đại lượng đo.
D.3. Giá trị “thực” và giá trị được hiệu chính
D.3.1. Kết quả đo đại lượng thể hiện được hiệu chỉnh cho sự khác nhau giữa đại lượng đó và đại lượng đo để dự đoán kết quả đo có được nếu đại lượng thể hiện thực sự thỏa mãn đầy đủ định nghĩa về đại lượng đo. Kết quả đo đại lượng thể hiện cũng được hiệu chính đối với tất cả các ảnh hưởng hệ thống có ý nghĩa được công nhận khác. Mặc dù kết quả hiệu chính cuối cùng đôi khi được coi là ước lượng tốt nhất của giá trị “thực” của đại lượng đo, nhưng thực tế kết quả đơn giản là ước lượng tốt nhất của giá trị đại lượng dự định được đo.
D.3.2. Ví dụ, giả sử đại lượng đo là độ dày của miếng vật liệu đã cho ở nhiệt độ xác định. Mẫu đó được đưa tới nhiệt độ gần với nhiệt độ xác định trên và độ dày của nó ở vị trí cụ thể được đo bằng micrômét kế. Độ dày của vật liệu ở vị trí và nhiệt độ đó, dưới áp suất do micrômét kế tác dụng là đại lượng thể hiện.
D.3.3. Nhiệt độ của vật liệu ở thời điểm đó và áp suất áp dụng được xác định. Kết quả chưa được hiệu chính của phép đo đại lượng thể hiện sau đó được hiệu chính bằng cách tính đến đường cong hiệu chuẩn của micrômét kế, chênh lệch nhiệt độ của mẫu vật so với nhiệt độ xác định và sự nén nhẹ mẫu vật dưới áp suất áp dụng.
D.3.4. Kết quả đã hiệu chính có thể được gọi là ước lượng tốt nhất của giá trị “thực”, “thực” với nghĩa giá trị của đại lượng được tin là đáp ứng hoàn toàn định nghĩa về đại lượng đo; nhưng khi micrômét kế được sử dụng cho phần khác của vật liệu thì đại lượng thể hiện khác với một giá trị “thực” khác. Tuy nhiên, giá trị “thực” phù hợp với định nghĩa của đại lượng đo vì phần nói đến sau không quy định rằng độ dày được xác định ở vị trí cụ thể trên miếng vật liệu đó. Vì vậy trong trường hợp này, do định nghĩa không đầy đủ của đại lượng đo nên giá trị “thực” có độ không đảm bảo có thể đánh giá được từ các phép đo được thực hiện ở các vị trí khác nhau trên miếng vật liệu đó. Ở mức độ nhất định, mỗi đại lượng đo có một độ không đảm bảo “nội tại”, về nguyên tắc có thể ước lượng được bằng một cách thức nào đó. Đây là độ không đảm bảo tối thiểu có thể xác định được cho đại lượng đo và mỗi phép đo đạt được độ không đảm bảo đó có thể được coi là phép đo tốt nhất có thể có của đại lượng đo. Để thu được giá trị đại lượng có độ không đảm bảo nhỏ hơn cần định nghĩa đại lượng đo đầy đủ hơn.
CHÚ THÍCH 1: Trong ví dụ, quy định kỹ thuật của đại lượng đo còn nhiều vấn để nghi ngờ khác có thể ảnh hưởng thấy được đến độ dày như: áp suất khí quyển, độ ẩm, tư thế của miếng vật liệu trong trường hấp dẫn, cách gá lắp, v.v…
CHÚ THÍCH 2: Mặc dù đại lượng đo cần được định nghĩa đủ chi tiết rằng độ không đảm bảo bất kỳ phát sinh từ định nghĩa không đầy đủ của nó là không đáng kể so với độ chính xác yêu cầu của phép đo, nhưng phải thừa nhận rằng điều này không phải lúc nào cũng khả thi. Ví dụ, định nghĩa có thể không đầy đủ vì nó không quy định tham số có thể được giả định, không hợp lý, có ảnh hưởng không đáng kể; hoặc nó có thể gợi ý các điều kiện không bao giờ có thể đáp ứng đầy đủ và khó tính đến việc thể hiện không hoàn hảo. Ví dụ, trong ví dụ của D.1.2, vận tốc của âm thanh hàm ý là sóng phẳng vô hạn có biên độ vô cùng nhỏ. Trong chừng mực phép đo không đáp ứng các điều kiện này thì hiệu ứng nhiễu xạ và phi tuyến cần được xem xét.
CHÚ THÍCH 3: Quy định kỹ thuật không đầy đủ về đại lượng đo có thể dẫn tới sự không nhất quán giữa kết quả đo của cùng một đại lượng được thực hiện ở các phòng thí nghiệm khác nhau.
D.3.5. Thuật ngữ “giá trị thực của đại lượng đo” hoặc của đại lượng (thường được viết tắt là “giá trị thực”) được tránh trong tiêu chuẩn này vì từ “thực” bị coi là thừa. “Đại lượng đo” (xem B.2.9) có nghĩa là “đại lượng cụ thể được đo”, vì lý do đó “giá trị của đại lượng đo” có nghĩa là “giá trị của đại lượng cụ thể tùy theo phép đo”. Do “đại lượng cụ thể: thường được hiểu là đại lượng xác định hoặc quy định (xem B.2.1, Chú thích 1), tính từ “thực” trong “giá trị thực của đại lượng đo” (hoặc trong “giá trị thực của đại lượng” là không cần thiết – giá trị “thực” của đại lượng đo (hoặc đại lượng) đơn giản là giá trị của đại lượng đo (hoặc đại lượng). Hơn nữa, như đã trình bày trong phần thảo luận ở trên, giá trị “thực” duy trì chỉ là khái niệm lý tưởng hóa.
D.4. Sai số
Kết quả đo đã hiệu chính không phải là giá trị của đại lượng đo – đó là do, nó có sai số – vì phép đo đại lượng được thể hiện không hoàn hảo do sự biến đổi ngẫu nhiên các quan trắc (ảnh hưởng ngẫu nhiên), việc xác định không thích hợp các số hiệu chính cho ảnh hưởng hệ thống và sự hiểu biết không đầy đủ về hiện tượng vật lý cụ thể (cũng là ảnh hưởng hệ thống). Giá trị của đại lượng được thể hiện và giá trị của đại lượng đo chưa bao giờ có thể được biết chính xác; tất cả những gì có thể biết là giá trị ước lượng của chúng. Trong ví dụ ở trên, độ dày đo được của tấm vật liệu có thể có sai số, nghĩa là, có thể khác so với giá trị của đại lượng đo (độ dày của tấm vật liệu), vì mỗi trong số các yếu tố sau có thể kết hợp đóng góp vào sai số chưa biết với kết quả đo:
a) khác biệt nhỏ giữa chỉ số của micrômét kế khi áp dụng lặp lại với cùng đại lượng được thể hiện;
b) hiệu chuẩn micrômét kế không đầy đủ;
c) phép đo nhiệt độ và áp suất áp dụng không đầy đủ;
d) hiểu biết không đầy đủ về ảnh hưởng của nhiệt độ, áp suất khí quyển và độ ẩm trên mẫu thử hoặc micromét kế hoặc cả hai.
D.5. Độ không đảm bảo
D.5.1. Trong khi giá trị chính xác của đóng góp vào sai số của kết quả đo chưa được biết và không thể biết thì có thể đánh giá được độ không đảm bảo liên quan đến các ảnh hưởng ngẫu nhiên và hệ thống làm phát sinh sai số. Nhưng, thậm chí nếu độ không đảm bảo được đánh giá là nhỏ thì vẫn không có sự đảm bảo rằng sai số trong kết quả đo là nhỏ; trong việc xác định sự hiệu chính hoặc đánh giá sự hiểu biết không đầy đủ, ảnh hưởng hệ thống có thể đã bị bỏ qua vì nó không được phát hiện. Do đó độ không đảm bảo của kết quả đo không nhất thiết là chỉ thị khả năng kết quả đo gần với giá trị của đại lượng đo; nó đơn giản là ước lượng khả năng nằm xích lại giá trị đúng nhất phù hợp với kiến thức hiện có.
D.5.2. Do đó độ không đảm bảo của phép đo là biểu thức của thực tế là, đối với đại lượng đo đã cho và kết quả đo đã cho của nó, không phải có một giá trị có vô số giá trị phân tán quanh kết quả phù hợp với tất cả các quan trắc, dữ liệu và sự hiểu biết của con người về thế giới tự nhiên, và có thể quy cho đại lượng đo các mức tin cậy khác nhau.
D.5.3. May mắn là không nhiều trường hợp đo thực tế, nhiều vấn đề đề cập trong phụ lục này không được áp dụng. Ví dụ, khi đại lượng đo được định nghĩa đủ tốt; khi các chuẩn hoặc phương tiện được hiệu chuẩn bằng cách sử dụng các chuẩn chính đã biết có thể liên kết tới chuẩn quốc gia; và khi độ không đảm bảo của các hiệu chính hiệu chuẩn là không đáng kể so với độ không đảm bảo phát sinh từ ảnh hưởng ngẫu nhiên lên số chỉ của phương tiện, hoặc từ số lượng hữu hạn các quan trắc (xem E.4.3). Tuy nhiên, sự hiểu biết không đầy đủ về các đại lượng ảnh hưởng và ảnh hưởng của chúng thường góp phần đáng kể vào độ không đảm bảo của kết quả đo.
D.6. Trình bày bằng đồ thị
D.6.1. Hình D.1 mô tả một số ý tưởng được đề cập trong Điều 3 của tiêu chuẩn này và trong phụ lục này. Hình minh họa vì sao trọng tâm của tiêu chuẩn này là độ không đảm bảo mà không phải sai số. Sai số chính xác của kết quả đo thường là không biết và không thể biết. Tất cả có thể làm là ước lượng giá trị của đại lượng đầu vào, bao gồm sự hiệu chính đối với các ảnh hưởng hệ thống được phát hiện, cùng với độ không đảm bảo chuẩn của chúng (độ lệch chuẩn ước lượng), từ các phân bố xác suất chưa biết được lấy mẫu bằng trung bình các quan trắc lặp lại hoặc từ phân bố chủ quan hoặc tiên nghiệm dựa trên tổ hợp thông tin có sẵn; và sau đó tính toán kết quả đo từ các giá trị ước lượng của đại lượng đầu vào và độ không đảm bảo chuẩn tổng hợp của kết quả đo từ độ không đảm bảo chuẩn của các giá trị ước lượng. Chỉ khi có cơ sở vững chắc để tin rằng tất cả những điều này được thực hiện đúng, không bỏ sót ảnh hưởng hệ thống đáng kể nào, thì mới có thể giả định rằng kết quả đo là ước lượng đáng tin cậy của giá trị đại lượng đo và độ không đảm bảo chuẩn tổng hợp của nó là thước đo đáng tin cậy của sai số có thể có.
CHÚ THÍCH 1: Trong Hình D.1a), các quan trắc được trình bày dưới dạng đồ thị nhằm mục đích minh họa [xem 4.4.3 và Hình 1b)].
CHÚ THÍCH 2: Sự hiệu chính sai số bằng âm của ước lượng sai số. Do đó trong Hình D.1 và Hình D.2, mũi tên minh họa sự hiệu chính sai số có độ dài bằng nhau nhưng có hướng ngược với mũi tên minh họa sai số, và ngược lại. Phần lời của hình ghi rõ mũi tên cụ thể minh họa sự hiệu chính hay sai số.
D.6.2. Hình D.2 mô tả cùng các vấn đề đã được minh họa trong Hình D.1 nhưng theo một cách khác. Hơn nữa, nó cũng mô tả ý tưởng là có thể có nhiều giá trị của đại lượng đo nếu định nghĩa của đại lượng đo không đầy đủ [mục g) của Hình D.2]. Độ không đảm bảo phát sinh từ sự không đầy đủ của định nghĩa này khi đo bởi phương sai được đánh giá từ phép đo nhiều thể hiện của đại lượng đo, bằng cách sử dụng cùng phương pháp, thiết bị … (xem D.3.4).
CHÚ THÍCH: Trong cột có tiêu đề “Phương sai”, thì phương sai được hiểu là phương sai ![]() được xác định ở Phương trình (11a) trong 5.1.3; do đó chúng bổ sung tuyến tính như đã trình bày.
được xác định ở Phương trình (11a) trong 5.1.3; do đó chúng bổ sung tuyến tính như đã trình bày.
|
Trung bình cộng chưa được hiệu chính của quan trắc |
Trung bình cộng của hiệu chính của quan trắc |
|
|
|
|
a) Khái niệm dựa trên đại lượng có thể quan trắc |
|
|
|
|
|
b) Khái niệm lý tưởng dựa trên đại lượng không thể quan trắc |
|
|
Hình D.1 – Minh họa bằng đồ thị giá trị, sai số và độ không đảm bảo |
|
|
Đại lượng |
Giá trị |
Phương sai |
|
a) Quan trắc chưa hiệu chính b) Trung bình cộng chưa hiệu chính của quan trắc c) Sự hiệu chính đối với tất cả ảnh hưởng hệ thống đã biết d) Kết quả đo e) Sai số tồn tại f) Giá trị của đại lượng đo g) Giá trị của đại lượng đo do định nghĩa không đầy đủ h) Kết quả cuối cùng của phép đo. |
|
|
Hình D.2 – Minh họa bằng đồ thị giá trị, sai số và độ không đảm bảo
PHỤ LỤC E
(tham khảo)
ĐỘNG LỰC VÀ CƠ SỞ CHO KHUYẾN NGHỊ INC-1 (1980)
Phụ lục này đưa ra thảo luận ngắn gọn về động lực và cơ sở thống kê cho Khuyến nghị INC-1 (1980) của Nhóm công tác Trình bày độ không đảm bảo mà tiêu chuẩn này dựa vào. Phần thảo luận kỹ hơn, xem Tài liệu tham khảo [1, 2, 11, 12].
E.1. “An toàn”, “ngẫu nhiên” và “hệ thống”
E.1.1. Tiêu chuẩn này trình bày phương pháp có khả năng áp dụng rộng rãi để đánh giá và trình bày độ không đảm bảo đo. Nó cung cấp một giá trị thực tế hơn là giá trị “an toàn” của độ không đảm bảo trên cơ sở quan niệm là không có sự khác nhau vốn có nào giữa thành phần độ không đảm bảo phát sinh từ ảnh hưởng ngẫu nhiên và từ sự hiệu chính ảnh hưởng hệ thống (xem 3.2.2 và 3.2.3). Do đó, phương pháp này có sự khác biệt so với các phương pháp đã biết trước đây ở hai ý tưởng dưới đây.
E.1.2. Ý tưởng thứ nhất là độ không đảm bảo được báo cáo cần “an toàn” hoặc “vừa phải”, nghĩa là không bao giờ được phạm sai lầm thiên về phía quá nhỏ. Thực tế, vì việc đánh giá độ không đảm bảo của kết quả đo là khó hiểu nên nó thường bị làm lớn có chủ ý.
E.1.3. Ý tưởng thứ hai là các ảnh hưởng gây ra độ không đảm bảo luôn nhận biết được là “ngẫu nhiên” hoặc “hệ thống” với bản chất khác nhau; độ không đảm bảo kèm theo từng loại được kết hợp theo cách riêng và được báo cáo riêng (hoặc khi một số được yêu cầu, thì tổng hợp theo một số cách nhất định). Thực tế, phương pháp tổng hợp độ không đảm bảo thường được thiết kế để đáp ứng yêu cầu an toàn.
E.2. Lý giải về đánh giá độ không đảm bảo thực tế
E.2.1. Khi giá trị của đại lượng đo được báo cáo, phải đưa ra ước lượng tốt nhất về giá trị của nó và đánh giá tốt nhất độ không đảm bảo của ước lượng đó, vì nếu độ không đảm bảo là sai, thì thường không thể quyết định theo hướng sai nào là “an toàn”. Việc nói giảm đi về độ không đảm bảo có thể gây nên sự tin tưởng quá mức vào giá trị được báo cáo, đôi khi gây lúng túng hoặc thậm chí hậu quả có hại. Việc nói quá lên có tính toán về độ không đảm bảo cũng có thể có hậu quả không mong muốn. Nó có thể làm cho người sử dụng thiết bị đo phải đầu tư cho thiết bị đắt hơn mức cần thiết, hoặc nó có thể làm cho sản phẩm đắt tiền bị loại bỏ không cần thiết hoặc dịch vụ của phòng thí nghiệm hiệu chuẩn bị từ chối.
E.2.2. Điều đó không phải để nói rằng cách đánh giá này sử dụng kết quả đo không thể áp dụng thừa số của chính nó cho độ không đảm bảo được công bố để thu được độ không đảm bảo mở rộng xác định một khoảng có mức tin cậy quy định và đáp ứng yêu cầu của chính người sử dụng, cũng không phải trong những trường hợp nhất định, các cơ quan cung cấp kết quả đo thường không thể áp dụng thừa số cung cấp độ không đảm bảo mở rộng đáp ứng yêu cầu của một nhóm người sử dụng cụ thể sử dụng kết quả của họ. Tuy nhiên, các thừa số này (luôn được công bố) phải được áp dụng cho độ không đảm bảo khi được xác định bằng phương pháp thực tế, và chỉ sau khi độ không đảm bảo được xác định sao cho khoảng được xác định bằng độ không đảm bảo mở rộng có mức tin cậy yêu cầu và có thể dễ dàng đảo lại phép tính.
E.2.3. Những người tham gia vào phép đo thường phải đưa vào phân tích của họ các kết quả đo do người khác thực hiện, mỗi kết quả đo khác này có một độ không đảm bảo của chính nó. Trong đánh giá độ không đảm bảo kết quả đo của mình, họ cần có giá trị tốt nhất, không phải giá trị “an toàn”, của độ không đảm bảo cho từng kết quả được tích hợp từ nguồn khác. Hơn nữa, phải có một cách hợp lý và đơn giản trong đó độ không đảm bảo thu được này có thể được kết hợp với độ không đảm bảo từ các quan trắc riêng để đưa ra độ không đảm bảo kết quả của riêng họ. Khuyến nghị INC-1 (1980) cung cấp cách đánh giá như vậy.
E.3. Lý giải việc xử lý tất cả các thành phần độ không đảm bảo theo cách giống nhau
Trọng tâm thảo luận của điều này là một ví dụ đơn giản minh họa cách tiêu chuẩn này xử lý thành phần độ không đảm bảo phát sinh từ ảnh hưởng ngẫu nhiên và sự hiệu chính cho ảnh hưởng hệ thống theo cùng một cách đánh giá độ không đảm bảo của kết quả đo. Do đó, ví dụ điển hình cho quan điểm được chấp nhận trong tiêu chuẩn này và trích dẫn trong E.1.1, đó là, tất cả thành phần của độ không đảm bảo có cùng bản chất và được xử lý giống nhau. Mở đầu của phần thảo luận là phép đạo hàm đơn giản biểu thức toán học đối với sự truyền độ lệch chuẩn, trong tiêu chuẩn này được gọi là định luật lan truyền độ không đảm bảo.
E.3.1. Để đại lượng đầu ra z = f(w1,w2,…,wN) phụ thuộc vào N đại lượng đầu vào w1, w2, …, wN, torng đó mỗi wi được mô tả bằng một phân bố xác suất phù hợp. Khai triển f quanh kỳ vọng của wi, E(wi) º mi, trong chuỗi Taylor bậc nhất mang lại cho các độ lệch nhỏ của z quanh mz theo các độ lệch nhỏ của wi quanh mi,
![]() (E.1)
(E.1)
Trong đó các số hạng bậc cao được giả định là không đáng kể và mz = f(m1,m2,…., mN). Khi đó bình phương độ lệch z – mz được cho bằng
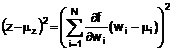 (E.2a)
(E.2a)
Có thể viết như sau
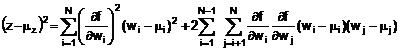 (E.2b)
(E.2b)
Kỳ vọng của độ lệch bình phương ![]() là phương sai của z, nghĩa là,
là phương sai của z, nghĩa là, ![]() , và đo đó từ phương trình (E.2b) ta có:
, và đo đó từ phương trình (E.2b) ta có:
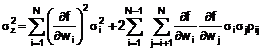 (E.3)
(E.3)
Trong biểu thức này, ![]() là phương sai của wi và pij = v(wi,wj)/(
là phương sai của wi và pij = v(wi,wj)/(![]()
![]() )1/2 là hệ số tương quan của wi và wj, trong đó v(wi,wj) = E[(wi – mi) – (wj – mj)] là hiệp phương sai của wi và wj.
)1/2 là hệ số tương quan của wi và wj, trong đó v(wi,wj) = E[(wi – mi) – (wj – mj)] là hiệp phương sai của wi và wj.
CHÚ THÍCH 1: ![]() và
và![]() tương ứng là mômen trung tâm bậc 2 (xem C.2.13 và C.2.22) của phân bố xác suất z và wi. Phân bố xác suất có thể đặc trưng đầy đủ bằng kỳ vọng, phương sai và mômen trung tâm bậc cao hơn.
tương ứng là mômen trung tâm bậc 2 (xem C.2.13 và C.2.22) của phân bố xác suất z và wi. Phân bố xác suất có thể đặc trưng đầy đủ bằng kỳ vọng, phương sai và mômen trung tâm bậc cao hơn.
CHÚ THÍCH 2: Phương trình (13) trong 5.2.2 [cùng với Phương trình (15)], được sử dụng để tính độ không đảm bảo chuẩn tổng hợp, giống với Phương trình (E.3) ngoại trừ việc Phương trình (13) được thể hiện theo ước lượng của phương sai, độ lệch chuẩn và hệ số tương quan.
E.3.2. Theo thuật ngữ truyền thống, Phương trình (E.3) thường được gọi là “định luật chung về lan truyền sai số”, tên gọi đó được áp dụng phù hợp hơn cho biểu thức dạng ![]() , trong đó ∆z là thay đổi của z theo thay đổi (nhỏ) ∆wi của wi [xem Phương trình (E.8)]. Trong thực tế, gọi Phương trình (E.3) là định luật lan truyền độ không đảm bảo như trong tiêu chuẩn này là phù hợp vì nó chỉ ra cách độ không đảm bảo của đại lượng đầu vào wi, được lấy theo các độ lệch chuẩn của phân bố xác suất của wi, kết hợp lại để đưa ra độ không đảm bảo của đại lượng đầu ra z nếu độ không đảm bảo đó được lấy bằng với độ lệch chuẩn của phân bố xác suất của z.
, trong đó ∆z là thay đổi của z theo thay đổi (nhỏ) ∆wi của wi [xem Phương trình (E.8)]. Trong thực tế, gọi Phương trình (E.3) là định luật lan truyền độ không đảm bảo như trong tiêu chuẩn này là phù hợp vì nó chỉ ra cách độ không đảm bảo của đại lượng đầu vào wi, được lấy theo các độ lệch chuẩn của phân bố xác suất của wi, kết hợp lại để đưa ra độ không đảm bảo của đại lượng đầu ra z nếu độ không đảm bảo đó được lấy bằng với độ lệch chuẩn của phân bố xác suất của z.
E.3.3. Phương trình (E.3) cũng được áp dụng cho sự lan truyền của bội các độ lệch chuẩn, nếu mỗi độ lệch chuẩn si được thay bằng tích ksi, với cùng k cho từng si thì độ lệch chuẩn của đại lượng đầu ra z sẽ được thay bằng ksz. Tuy nhiên, nó không áp dụng cho lan truyền khoảng tin cậy. Nếu mỗi si được thay bằng đại lượng di xác định khoảng tương ứng với mức tin cậy p đã cho thì đại lượng thu được với z, dz sẽ được xác định khoảng tương ứng với cùng giá trị p trừ khi tất cả wi được mô tả bằng phân bố chuẩn. Các giả định như thế về tính chuẩn của phân bố xác suất của các đại lượng wi không được bao hàm trong Phương trình (E.3). Cụ thể hơn, nếu trong Phương trình (10) ở 5.1.2 mỗi độ không đảm bảo chuẩn u(xi) được đánh giá từ các quan trắc lặp lại độc lập và nhân với hệ số t thích hợp với bậc tự do của nó đối với giá trị p cụ thể (lấy p = 95%), thì độ không đảm bảo của ước lượng y sẽ không xác định khoảng tương ứng với giá trị đó của p (xem G.3 và G.4).
CHÚ THÍCH: Yêu cầu về tính chuẩn khi lan truyền khoảng tin cậy bằng cách sử dụng Phương trình (E.3) có thể là một trong các lý do cho sự chia tách có tính lịch sử của các thành phần độ không đảm bảo thu được từ các quan trắc lặp lại, được giả định là theo phân bố chuẩn, từ đó nó được đánh giá đơn giản là cận trên và dưới.
E.3.4. Xét ví dụ sau: z chỉ phụ thuộc vào một đại lượng đầu vào w, z = f(w), trong đó w được ước lượng bằng cách lấy trung bình n giá trị wk của w; n giá trị này thu được từ n quan trắc lặp lại độc lập qk của biến ngẫu nhiên q; wk và qk liên hệ bằng:
wk = a + bqk (E.4)
Ở đây a là giá trị bù hay độ trội “hệ thống” không đổi chung cho từng quan trắc, b là hệ số thang đo chung. Giá trị bù và hằng số thang đo, mặc dù được cố định trong suốt quá trình quan trắc, nhưng vẫn được giả định là đặc trưng bởi phân bố xác suất tiên nghiệm, với a và b là các ước lượng tốt nhất của kỳ vọng trong các phân bố này.
Ước lượng tốt nhất của w là trung bình cộng hay giá trị trung bình của ![]() thu được từ:
thu được từ:
![]() (E.5)
(E.5)
Đại lượng z khi đó được ước lượng bằng f(![]() ) = f(a, b, q1, q2, …, qn) và ước lượng u2(z) của phương sai s2(z) thu được từ phương trình (E.3). Nếu để đơn giản, giả định rằng z = w sao cho ước lượng tốt nhất của z bằng z = f(
) = f(a, b, q1, q2, …, qn) và ước lượng u2(z) của phương sai s2(z) thu được từ phương trình (E.3). Nếu để đơn giản, giả định rằng z = w sao cho ước lượng tốt nhất của z bằng z = f(![]() ) =
) = ![]() , khi đó ước lượng u2(z) có thể tính được. Chú ý là phương trình (E.5):
, khi đó ước lượng u2(z) có thể tính được. Chú ý là phương trình (E.5):
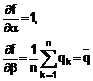
Và
![]()
Ký hiệu phương sai ước lượng của a và b tương ứng là u2(a) và u2(b), và giả định rằng các quan trắc riêng lẻ không tương quan, nhận được từ phương trình (E.3)
u2(z) = u2(a) + ![]() (E.6)
(E.6)
trong đó ![]() là phương tiện thực nghiệm của quan trắc qk tính theo phương trình (4) trong 4.2.2, và
là phương tiện thực nghiệm của quan trắc qk tính theo phương trình (4) trong 4.2.2, và ![]() /n =
/n = ![]() là phương sai thực nghiệm của trung bình
là phương sai thực nghiệm của trung bình ![]() [phương trình (5) trong 4.2.3]
[phương trình (5) trong 4.2.3]
E.3.5. Theo thuật ngữ truyền thống, số hạng thứ ba ở vế phải của phương trình (E.6) được gọi là đóng góp “ngẫu nhiên” vào phương sai ước lượng u2(z) vì nó thường giảm khi số quan trắc n tăng, trong khi hai số hạng đầu được gọi là đóng góp “hệ thống” vì chúng không phụ thuộc vào n.
Quan trọng hơn, trong một số cách xử lý không đảm bảo đo truyền thống, phương sai (E.6) bị nghi ngờ vì không có sự khác biệt được chỉ ra giữa độ không đảm bảo xuất hiện từ ảnh hưởng hệ thống và độ không đảm bảo xuất hiện từ ảnh hưởng ngẫu nhiên. Cụ thể, khi kết hợp các phương sai thu được từ phân bố xác xuất tiên nghiệm với các phương sai thu được từ phân bố trên cơ sở tần suất không được chấp nhận vì khái niệm xác suất tiên nghiệm với các phương sai thu được từ phân bố trên cơ sở tần suất không được chấp nhận vì khái niệm xác suất được coi là chỉ có khả năng áp dụng cho các biến cố có thể lặp lại nhiều lần dưới các điều kiện như nhau, với xác suất p của biến cố (0 £ p £ 1) chỉ ra rằng tần suất tương đối với biến cố này sẽ xảy ra.
Trái lại quan điểm phân bố trên cơ sở tần suất này, quan điểm hợp lý tương tự cho rằng xác suất là thước đo tin tưởng một biến cố sẽ xảy ra [13, 14]. Ví dụ, giả sử một người có khả năng thắng một khoản tiền nhỏ D và một người là người cá cược có lý trí. Độ tin tưởng của một người về sự xuất hiện biến cố A là p = 0,5 nếu người đó không quan tâm tới hai lựa chọn dưới đây:
1) nhận được D nếu biến cố A xảy ra nhưng không nhận được gì nếu biến cố không xảy ra;
2) nhận được D nếu biến cố A không xảy ra nhưng có gì nếu biến cố xảy ra.
Khuyến nghị INC-1 (1980) mà tiêu chuẩn này dựa trên đó thừa nhận quan điểm xác suất này vì nó coi biểu thức như phương trình (E.6) là cách phù hợp để tính độ không đảm bảo chuẩn tổng hợp của kết quả đo.
E.3.6. Có ba ưu điểm nổi bật để thừa nhận cách giải thích xác suất dựa trên độ tin tưởng, độ lệch chuẩn (độ không đảm bảo chuẩn) và định luật lan truyền độ không đảm bảo [phương trình (E.3)] là cơ sở cho việc đánh giá và trình bày độ không đảm bảo đo, như trong tiêu chuẩn này:
a) định luật lan truyền độ không đảm bảo cho phép độ không đảm bảo chuẩn tổng hợp của một kết quả đo được hợp nhất dễ dàng trong việc đánh giá độ không đảm bảo chuẩn tổng hợp của kết quả khác mà nó được dùng lần đầu tiên;
b) độ không đảm bảo chuẩn tổng hợp có thể dùng làm cơ sở để tính các khoảng tương ứng với độ tin cậy yêu cầu của chúng theo cách thực tế; và
c) không cần thiết phân loại các thành phần như “ngẫu nhiên” hoặc “hệ thống” (hoặc theo cách khác) khi đánh giá độ không đảm bảo vì tất cả các thành phần của độ không đảm bảo đều được xử lý theo cùng một cách.
Lợi ích c) rất lớn vì sự phân loại này thường là nguồn gốc gây nhầm lẫn; thành phần độ không đảm bảo không phải là “ngẫu nhiên” hay “hệ thống”. Bản chất của nó được quy định bởi việc sử dụng tạo ra từ đại lượng tương ứng, hoặc chính thức hơn, bởi tình huống trong đó đại lượng xuất hiện trong mô hình toán mô tả phép đo. Do đó, khi đại lượng tương ứng được sử dụng trong tình huống khác nhau thì thành phần “ngẫu nhiên” có thể trở thành thành phần “hệ thống” và ngược lại.
E.3.7. Vì lý do nêu ra trong c) ở trên, Khuyến nghị INC-1 (1980) không phân loại các thành phần của độ không đảm bảo thành “ngẫu nhiên” hay “hệ thống”. Thực tế, cho đến khi việc tính độ không đảm bảo chuẩn tổng hợp của kết quả đo được đề cập thì không có nhu cầu phân loại thành phần độ không đảm bảo và do đó thực sự không cần có bất cứ sơ đồ phân loại nào.Tuy nhiên, vì các nhãn thuận lợi đôi khi có thể có ích trong việc trao đổi thông tin và thảo luận ý tưởng, Khuyến nghị INC-1 (1980) cung cấp chương trình phân loại hai phương pháp riêng, “A” và “B”, mà theo đó thành phần độ không đảm bảo có thể được đánh giá (xem 0.7, 2.3.2 và 2.3.3).
Việc phân loại các phương pháp được sử dụng để đánh giá thành phần độ không đảm bảo nhằm tránh vấn đề chính liên quan tới phân loại bản thân các thành phần, cụ thể là, sự phụ thuộc của việc phân loại thành phần vào đại lượng tương ứng được sử dụng như thế nào. Tuy nhiên, sự phân loại phương pháp chứ không phải thành phần không cản trở việc gộp các thành phần riêng lẻ được đánh giá bằng hai phương pháp trên vào các nhóm riêng cho mục đích cụ thể trong phép đo đã cho, ví dụ, khi so sánh sự biến động quan trắc thực nghiệm và sự thay đổi dự đoán lý thuyết của các giá trị đầu ra của một hệ thống đo phức tạp (xem 3.4.3).
E.4. Độ lệch chuẩn là thước đo độ không đảm bảo
E.4.1. Phương pháp (E.3) yêu cầu rằng dù độ không đảm bảo của ước lượng đại lượng đầu vào thu được bằng cách nào thì nó phải được đánh giá như độ không đảm bảo chuẩn, nghĩa là, như độ lệch chuẩn ước lượng. Nếu thay vào đó là sự “an toàn” được đánh giá thì nó không thể được sử dụng trong phương pháp (E.3). Cụ thể, nếu “biên sai số cực đại” (độ lệch có thể hiểu lớn nhất từ ước lượng được coi là tốt nhất) sử dụng trong Phương pháp (E.3), độ không đảm bảo thu được sẽ không có ý nghĩa và sẽ không sử dụng được bởi người mong muốn đưa vào tính toán sau đó độ không đảm bảo của đại lượng khác (xem E.3.3).
E.4.2. Khi độ không đảm bảo của đại lượng đầu vào không thể đánh giá được bằng việc phân tích kết quả của một số thích hợp các quan trắc lặp lại thì phải chấp nhận phân bố xác suất dựa vào hiểu biết kém bao quát hơn so với mong muốn. Tuy nhiên, điều đó không làm phân bố mất giá trị hoặc không thực; giống như các phân bố xác suất, đó là sự thể hiện hiểu biết hiện có.
E.4.3. Các đánh giá dựa trên cơ sở các quan trắc lặp lại không hẳn là tốt hơn so với những đánh giá thu được bằng các phương pháp khác. Xét s(![]() ), độ lệch chuẩn thực nghiệm của trung bình n quan trắc độc lập qk của biến ngẫu nhiên có phân bố chuẩn q [xem phương trình (5) trong 4.2.3]. Đại lượng s(
), độ lệch chuẩn thực nghiệm của trung bình n quan trắc độc lập qk của biến ngẫu nhiên có phân bố chuẩn q [xem phương trình (5) trong 4.2.3]. Đại lượng s(![]() ) là một thống kê (xem C.2.23) để ước lượng s(
) là một thống kê (xem C.2.23) để ước lượng s(![]() ), độ lệch chuẩn của phân bố xác suất
), độ lệch chuẩn của phân bố xác suất ![]() , nghĩa là, độ lệch chuẩn của phân bố các giá trị
, nghĩa là, độ lệch chuẩn của phân bố các giá trị ![]() thu được nếu phép đo được lặp lại vô số lần. Phương sai s2[s(
thu được nếu phép đo được lặp lại vô số lần. Phương sai s2[s(![]() )] của s(
)] của s(![]() ) được cho xấp xỉ bằng:
) được cho xấp xỉ bằng:
s2[s(![]() )] = s2(
)] = s2(![]() )/(2v) (E.7)
)/(2v) (E.7)
Trong đó v = n -1 là bậc tự do của s(![]() ) (xem G.3.3). Do đó, độ lệch chuẩn tương đối của s(
) (xem G.3.3). Do đó, độ lệch chuẩn tương đối của s(![]() ), được cho bằng tỉ số s[s(
), được cho bằng tỉ số s[s(![]() )]/s(
)]/s(![]() ) và có thể được lấy làm thước đo độ không đảm bảo tương đối của s(
) và có thể được lấy làm thước đo độ không đảm bảo tương đối của s(![]() ), xấp xỉ bằng [2(n-1)]-1/2. “Độ không đảm bảo của độ không đảm bảo” này của (
), xấp xỉ bằng [2(n-1)]-1/2. “Độ không đảm bảo của độ không đảm bảo” này của (![]() ), xuất hiện thuần túy từ nguyên nhân thống kê của việc lấy mẫu hạn chế, có thể rất lớn; với n = 10 là 24%. Giá trị này và các giá trị khác được cho trong Bảng E.1, cho thấy độ lệch chuẩn của độ lệch chuẩn ước lượng thống kê là đáng kể đối với giá trị thực tế của n. Do đó có thể kết luận rằng đánh giá độ không đảm bảo Loại A không nhất thiết đáng tin cậy hơn đánh giá Loại B và trong nhiều tình huống đo thực tế, trong đó số lượng quan trắc có hạn, các thành phần thu được từ đánh giá Loại B có thể được biết tốt hơn các thành phần thu được từ đánh giá Loại A.
), xuất hiện thuần túy từ nguyên nhân thống kê của việc lấy mẫu hạn chế, có thể rất lớn; với n = 10 là 24%. Giá trị này và các giá trị khác được cho trong Bảng E.1, cho thấy độ lệch chuẩn của độ lệch chuẩn ước lượng thống kê là đáng kể đối với giá trị thực tế của n. Do đó có thể kết luận rằng đánh giá độ không đảm bảo Loại A không nhất thiết đáng tin cậy hơn đánh giá Loại B và trong nhiều tình huống đo thực tế, trong đó số lượng quan trắc có hạn, các thành phần thu được từ đánh giá Loại B có thể được biết tốt hơn các thành phần thu được từ đánh giá Loại A.
E.4.4. Có lập luận cho rằng, trong khi độ không đảm bảo gắn với việc áp dụng một phương pháp đo cụ thể là các tham số thống kê đặc trưng cho biến ngẫu nhiên, có những trường hợp “ảnh hưởng hệ thống thực sự” mà độ không đảm bảo của nó phải được xử lý khác. Ví dụ là sự bù có giá trị cố định chưa biết là như nhau đối với mọi cách xác định bằng phương pháp do sai sót có thể có trong chính nguyên lý của bản thân phương pháp hoặc của một trong các giả định cơ bản. Nhưng nếu khả năng của sự bù như vậy được thừa nhận là có và độ lớn được cho là đáng kể thì nó có thể được mô tả bằng phân bố xác suất, dù được xây dựng đơn giản đến đâu, dựa trên sự hiểu biết dẫn tới kết luận rằng nó có thể tồn tại và lớn đáng kể. Do đó, nếu coi xác suất là thước đo của sự tin tưởng một biến cố sẽ xảy ra thì đóng góp của ảnh hưởng hệ thống như vậy có thể được tính đến trong độ không đảm bảo chuẩn tổng hợp của kết quả đo bằng cách đánh giá nó như độ không đảm bảo chuẩn của phân bố xác suất tiên nghiệm và xử lý theo cách giống như độ không đảm bảo chuẩn khác của đại lượng đầu vào.
VÍ DỤ: Quy định kỹ thuật của thủ tục đo cụ thể yêu cầu một đại lượng đầu vào nào đó được tính toán từ sự khai triển chuỗi lũy thừa cụ thể mà các số hạng bậc cao không được biết chính xác. Ảnh hưởng hệ thống do không thể xử lý chính xác các số hạng này dẫn tới sự bù cố định chưa biết mà nó không thể được lấy mẫu thực nghiệm bằng cách lặp lại thủ tục. Do đó, độ không đảm bảo gắn với ảnh hưởng trên không thể được đánh giá và được tính đến trong độ không đảm bảo của kết quả đo cuối cùng nếu giải thích dựa trên tần suất của xác suất được tuân thủ chặt chẽ. Tuy nhiên, giải thích xác suất trên cơ sở độ tin tưởng cho phép độ không đảm bảo đặc trưng cho ảnh hưởng được đánh giá từ phân bố xác suất tiên nghiệm (được suy ra từ sự hiểu biết có sẵn về các số hạng được biết không chính xác) và được tính đến trong tính toán độ không đảm bảo chuẩn tổng hợp của kết quả đo giống như bất kỳ độ không đảm bảo nào khác.
Bảng E.1 – s[s(![]() )]/s(
)]/s(![]() ), độ lệch chuẩn của độ lệch chuẩn thực nghiệm của trung bình
), độ lệch chuẩn của độ lệch chuẩn thực nghiệm của trung bình ![]() của n quan trắc độc lập thuộc biến ngẫu nhiên phân bố chuẩn q, liên quan đến độ lệch chuẩn của giá trị trung bình đó (a)(b)
của n quan trắc độc lập thuộc biến ngẫu nhiên phân bố chuẩn q, liên quan đến độ lệch chuẩn của giá trị trung bình đó (a)(b)
|
Số lượng quan trắc |
s[s( |
|
2 3 4 5 10 20 30 50 |
76 52 42 36 24 16 13 10 |
|
(a) Các giá trị trên được tính từ biểu thức chính xác đối với s[s( (b) Trong biểu thức s[s(
Kỳ vọng phương sai của s được cho bằng:
trong đó G(x) là hàm gamma. Chú ý là E[S] < s với số n hữu hạn. |
|
E.5. So sánh hai quan điểm về độ không đảm bảo
E.5.1. Trọng tâm của tiêu chuẩn này là kết quả đo và độ không đảm bảo được đánh giá của nó hơn là giá trị “thực” và sai số của đại lượng không thể biết (xem Phụ lục D). Theo quan điểm thực hành thì kết quả đo đơn giản là giá trị được quy cho đại lượng đo và độ không đảm bảo của kết quả là thước đo sự phân tán của giá trị có thể quy hợp lý cho đại lượng đo, tiêu chuẩn này có tác dụng xóa bỏ sự nhầm lẫn thường xuyên giữa độ không đảm bảo, giá trị “thực” không thể biết và sai số của đại lượng.
E.5.2. Mối quan hệ này có thể được hiểu bằng cách giải thích phương trình (3), định luật lan truyền độ không đảm bảo, từ quan điểm giá trị “thực” và sai số. Trong trường hợp này, mi được coi là giá trị “thực” duy nhất, chưa biết, của đại lượng đầu vào wi và mỗi wi được giả định là liên quan đến giá trị “thực” mi bằng wi = mi + ei trong đó ei là sai số trong wi. Kỳ vọng của phân bố xác suất của từng ei được giả định bằng “không”, E(ei) = 0, với phương sai ![]() . Khi đó phương trình (E.1) trở thành:
. Khi đó phương trình (E.1) trở thành:
![]() (E.8)
(E.8)
Trong đó ez = z – mz là sai số của z và mz là giá trị “thực” của z. Nếu khi đó lấy kỳ vọng của bình phương ez thì thu được phương trình giống dạng của phương trình (E.3) nhưng trong đó ![]() là phương sai của ez và
là phương sai của ez và ![]() là hệ số tương quan của ei và ej, trong đó v(ei,ej) = E(ei,ej) là hiệp phương sai của ei và ej. Phương sai và hệ số tương quan, do đó, gắn với sai số của đại lượng đầu vào hơn là với bản thân đại lượng đầu vào.
là hệ số tương quan của ei và ej, trong đó v(ei,ej) = E(ei,ej) là hiệp phương sai của ei và ej. Phương sai và hệ số tương quan, do đó, gắn với sai số của đại lượng đầu vào hơn là với bản thân đại lượng đầu vào.
CHÚ THÍCH: Giả định rằng xác suất được coi là thước đo của sự tin tưởng là biến cố sẽ xảy ra, ngụ ý rằng sai số hệ thống có thể được xử lý theo cách giống với sai số ngẫu nhiên và ei được thể hiện theo loại này hay loại kia.
E.5.3. Trong thực tế, sự khác nhau trong quan điểm không dẫn tới sự khác nhau về trị số của kết quả đo hoặc độ không đảm bảo ấn định cho kết quả đó.
Thứ nhất, trong cả hai trường hợp, ước lượng sẵn có tốt nhất của đại lượng đầu vào wi được sử dụng để thu được ước lượng tốt nhất của z từ hàm f; nó không tạo ra sự khác nhau trong tính toán nếu ước lượng tốt nhất được xem là giá trị thích hợp nhất để quy cho đại lượng theo yêu cầu hoặc ước lượng tốt nhất của giá trị “thực” của chúng.
Thứ hai, vì ei = wi – mi, và vì mi là giá trị cố định duy nhất và do đó không có độ không đảm bảo, nên phương sai và độ lệch chuẩn của ei và wi là như nhau. Điều này có nghĩa là trong cả hai trường hợp, độ không đảm bảo chuẩn được sử dụng như ước lượng của độ lệch chuẩn si để thu độ không đảm bảo chuẩn tổng hợp của kết quả đo là như nhau và sẽ tạo ra trị số giống nhau cho độ không đảm bảo đó. Một lần nữa, nó không tạo ra sự khác nhau nào trong tính toán nếu độ không đảm bảo được xem là thước đo độ phân tán của phân bố xác suất của đại lượng đầu vào hoặc là thước đo độ phân tán phân bố xác suất của sai số của đại lượng đó.
CHÚ THÍCH: Nếu giả định trong chú thích của E.5.2 không được đưa ra thì thông tin trong điều này không được áp dụng trừ khi tất cả các ước lượng của đại lượng đầu vào và độ không đảm bảo của các ước lượng đó thu được từ phân tích thống kê các quan trắc lặp lại, nghĩa là, từ đánh giá Loại A.
E.5.4. Trong khi cách tiếp cận trên cơ sở giá trị “thực” và sai số tạo ra các kết quả bằng số giống nhau như cách tiếp cận được thực hiện trong tiêu chuẩn này (với điều kiện giả định trong chú thích của E.5.2 được thực hiện), thì khái niệm về độ không đảm bảo của tiêu chuẩn này sẽ loại trừ sự nhầm lẫn giữa sai số và độ không đảm bảo (xem Phụ lục D). Thực ra, cách tiếp cận của tiêu chuẩn này, trong đó trọng tâm là về giá trị được quan trắc (hoặc được ước lượng) của đại lượng và sự biến thiên được quan trắc (hoặc được ước lượng) của giá trị đó, làm cho mọi quan tâm về sai số là hoàn toàn không cần thiết.
PHỤ LỤC F
(tham khảo)
HƯỚNG DẪN THỰC HÀNH VỀ ĐÁNH GIÁ THÀNH PHẦN ĐỘ KHÔNG ĐẢM BẢO
Phụ lục này đưa thêm các gợi ý về đánh giá các thành phần độ không đảm bảo, chủ yếu mang tính chất thực hành nhằm bổ sung cho các gợi ý nêu trong Điều 4.
F.1. Các thành phần được đánh giá từ quan trắc lặp lại: Đánh giá độ không đảm bảo chuẩn Loại A
F.1.1. Các quan trắc ngẫu nhiên và lặp lại
F.1.1.1. Độ không đảm bảo được xác định từ các quan trắc lặp lại thường trái ngược với độ không đảm bảo được đánh giá bằng các cách khác về “tính khách quan”, “tính nghiêm ngặt thống kê”… Điều đó không có nghĩa là chúng chỉ có thể được đánh giá bằng việc áp dụng các công thức thống kê cho các quan trắc và việc đánh giá chúng không yêu cầu áp dụng việc phán đoán.
F.1.1.2. Đầu tiên phải đặt câu hỏi, “các quan trắc lặp lại hoàn toàn độc lập với sự lặp lại của thủ tục đo tới mức độ nào?” Nếu tất cả các quan trắc trên mẫu đơn và nếu việc lấy mẫu là một phần của thủ tục đo vì đại lượng đó là tính chất của vật liệu (ngược với tính chất của mẫu vật liệu đã cho), thì quan trắc không lặp lại độc lập; sự đánh giá thành phần của phương sai xuất hiện từ sự khác nhau có thể có giữa các mẫu phải được bổ sung vào phương sai quan trắc của quan trắc lặp lại được thực hiện trên mẫu đơn.
Nếu việc điều chỉnh phương tiện đo về “không” là một phần của thủ tục đo thì phương tiện đo phải được điều chỉnh lại về “không” như một phần của từng phép lặp lại, thậm chí nếu có độ trôi không đáng kể trong thời gian quan trắc được thực hiện, vì có khả năng có độ không đảm bảo xác định được bằng thống kê có thể quy cho việc điều chỉnh về “không”.
Tương tự, nếu phải đọc khí áp kế thì theo nguyên tắc cần đọc cho từng lần lặp lại của phép đo (tốt nhất là sau khi làm thay đổi nó và để nó trở về trạng thái cân bằng), vì có thể có biến động về số chỉ và việc đọc, ngay cả khi áp suất khí quyển không đổi.
F.1.1.3. Thứ hai, phải đặt câu hỏi xem tất cả các ảnh hưởng được giả định là ngẫu nhiên có thật sự ngẫu nhiên hay không. Trung bình và phương sai của phân bố có là hằng số không, hoặc có độ trôi trong giá trị của đại lượng ảnh hưởng không được đo trong suốt thời gian quan trắc lặp lại không? Nếu có đủ số quan trắc, thì trung bình cộng của kết quả thuộc nửa thứ nhất và thứ hai của chu kỳ và độ lệch chuẩn thực nghiệm có thể được tính toán và hai trung bình này được so sánh với nhau để xét đoán xem sự khác nhau giữa chúng có ý nghĩa thống kê không và do đó có sự ảnh hưởng thay đổi theo thời gian không.
F.1.1.4. Nếu giá trị của “dịch vụ chung” trong phòng thí nghiệm (điện áp nguồn và tần số, áp lực nước và nhiệt độ, áp suất nitơ…) là các đại lượng ảnh hưởng thì thường có yêu tố không ngẫu nhiên trong các biến đổi của chúng không thể bị bỏ qua.
F.1.1.5. Nếu chữ số có ý nghĩa nhỏ nhất của số chỉ dạng số thay đổi liên tục trong suốt quá trình quan trắc do “nhiễu” thì đôi khi khó để không chọn giá trị ưu tiên riêng chưa biết của số đó. Tốt hơn nên có biện pháp dừng chỉ thị ở thời điểm bất kỳ và ghi lại kết quả đo.
F.1.2. Sự tương quan
Nhiều thảo luận trong điều này cũng có thể áp dụng cho đánh giá độ không đảm bảo chuẩn Loại B.
F.1.2.1. Hiệp phương sai gắn với hai đại lượng đầu vào Xi và Xj có thể được lấy bằng “không” hoặc coi là vô nghĩa nếu
a) Xi và Xj không tương quan (các biến ngẫu nhiên, không phải là đại lượng vật lý được giả định là không đổi – xem 4.1.1, Chú thích 1), ví dụ, vì chúng được đo lặp lại nhưng không đồng thời trong các thực nghiệm độc lập khác nhau hoặc vì chúng đại diện cho đại lượng có được của các đánh giá khác nhau đã được tiến hành độc lập, hoặc nếu
b) Xi hoặc Xj có thể được coi là hằng số, hoặc là
c) thiếu thông tin để đánh giá hiệp phương sai gắn với ước lượng của Xi và Xj.
CHÚ THÍCH 1: Mặt khác, trong một vài trường hợp nhất định, như ví dụ về điện trở chuẩn của Chú thích 1 trong 5.2.2, rõ ràng các đại lượng đầu vào hoàn toàn tương quan và độ không đảm bảo chuẩn của chúng kết hợp tuyến tính.
CHÚ THÍCH 2: Các thực nghiệm khác nhau có thể không độc lập nếu, ví dụ, sử dụng cùng phương tiện trong từng thực nghiệm (xem F.1.2.3).
F.1.2.2. Dù hai đại lượng đầu vào được quan trắc lặp lại đồng thời có tương quan hay không thì vẫn có thể được xác định bằng phương trình (17) trong 5.2.3. Ví dụ, nếu tần số của bộ tạo dao động không được bù hoặc bù ít cho nhiệt độ là đại lượng đầu vào, nếu nhiệt độ môi trường cũng là đại lượng đầu vào và nếu chúng được quan trắc đồng thời, thì có thể có sự tương quan đáng kể được phát hiện bằng hiệp phương sai tính được của tần số của bộ tạo dao động và nhiệt độ môi trường.
F.1.2.3. Trong thực tế, đại lượng đầu vào thường tương quan vì cùng một chuẩn đo lường vật lý, phương tiện đo, số liệu tra cứu hoặc thậm chí phương tiện đo có độ không đảm bảo đáng kể được sử dụng trong ước lượng giá trị của chúng. Không làm mất tính tổng quát, giả định hai đại lượng đầu vào X1 và X2 được ước lượng bằng x1 và x2 phụ thuộc vào tập hợp biến không tương quan Q1, Q2, …, QL. Do đó, X1 = F(Q1, Q2,…, QL) và X2 = G(Q1, Q2, …, QL), mặc dù một số trong các biến này có thể chỉ thực sự xuất hiện trong một hàm này và không xuất hiện trong hàm khác. Nếu u2(ql) là phương sai ước lượng gắn với ước lượng ql của Ql, khi đó phương sai ước lượng gắn với x1, từ phương trình (10) trong 5.1.2 là:
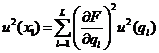 (F.1)
(F.1)
Với biểu thức tương tự cho u2(x2). Hiệp phương sai ước lượng gắn với x1 và x2 được cho bằng:
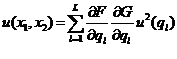 (F.2)
(F.2)
Ví chỉ các số hạng có ![]() # 0 và
# 0 và ![]() # 0 với l cho trước đóng góp vào tổng nên hiệp phương sai bằng “không” nếu không có biến chung cho F và G.
# 0 với l cho trước đóng góp vào tổng nên hiệp phương sai bằng “không” nếu không có biến chung cho F và G.
Hệ số tương quan ước lượng r(x1,x2) gắn với hai ước lượng x1 và x2 được xác định từ u(x1,x2) [phương trình (F.2)] và phương trình (14) trong 5.2.2, với u(x1) được tính toán từ phương trình (F.1) và u(x2) từ biểu thức tương tự. [Xem thêm phương trình (H.9) trong H.2.3] Cũng có khả năng hiệp phương sai ước lượng gắn với hai ước lượng đầu vào để có thành phần thống kê [xem phương trình (17) trong 5.2.3] và thành phần phát sinh như đã thảo luận trong điều này.
VÍ DỤ 1: Điện trở chuẩn Rs được sử dụng trong cùng phép đo để xác định cường độ dòng điện I và nhiệt độ t. Cường độ dòng điện được xác định bằng cách đo, hiệu điện thế đi qua các cực của chuẩn với vôn kế hiện số; nhiệt độ được xác định bằng cách đo, với cầu điện trở và chuẩn, điện trở Rt(t) của bộ cảm biến nhiệt điện trở đã được hiệu chuẩn có mối quan hệ nhiệt độ – điện trở trong dải 150C £ t £ 300C là ![]() , trong đó a và to là các hằng số đã biết. Do đó, dòng điện được xác định thông qua mối quan hệ I = Vs/Rs và nhiệt độ thông qua mối quan hệ
, trong đó a và to là các hằng số đã biết. Do đó, dòng điện được xác định thông qua mối quan hệ I = Vs/Rs và nhiệt độ thông qua mối quan hệ ![]() , trong đó b(t) là tỉ số đo được Rt(t)/Rs do cầu đo cung cấp.
, trong đó b(t) là tỉ số đo được Rt(t)/Rs do cầu đo cung cấp.
Do chỉ có đại lượng Rs là chung đối với biểu thức cho I và t, phương trình (F.2) mang lại cho hiệp phương sai của I và t:
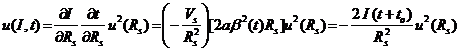
(Để đơn giản ký hiệu, trong ví dụ này một ký hiệu được sử dụng cho cả đại lượng đầu vào và ước lượng của nó.)
Để thu được trị số của hiệp phương sai, ta thay vào biểu thức này trị số của đại lượng đo được I và t, giá trị Rs và u(Rs) được cho trong giấy chứng nhận hiệu chuẩn của điện trở chuẩn. Đơn vị của u(I, t) là A0C vì thứ nguyên của phương sai tương đối [u(Rs)/Rs]2 bằng một (là đại lượng không thứ nguyên).
Hơn nữa, để đại lượng P liên hệ tới đại lượng đầu vào I và t bằng P = CoI2/(T0 + t), trong đó Co và To là các hằng số đã biết với độ không đảm bảo không đáng kể [u2(C0) » 0, u2(To) » 0]. Khi đó, phương trình (13) trong 5.2.2 dẫn tới phương sai của P theo phương sai của I và t và hiệp phương sai:
![]()
Phương sai u2(I) và u2(t) thu được nhờ áp dụng phương trình (10) của 5.1.2 vào mối quan hệ I = Vs/Rs và ![]() . Kết quả là:
. Kết quả là:
u2(I)/I2 = u2(Vs)/Vs2 + u2(Rs)/Rs2
u2(t) = 4(t + to)2u2(b)/b2 + 4(t + t0)2 u2(Rs)/Rs2
trong đó để đơn giản, giả định rằng độ không đảm bảo của hằng số t0 và a cũng không đáng kể. Các công thức này có thể sẵn sàng được đánh giá vì u2(Vs) và u2(b) có thể được xác định tương ứng từ số đọc lặp lại của vôn kế và cầu điện trở. Tất nhiên, độ không đảm bảo vốn có trong phương tiện đo và trong thủ tục đo được sử dụng cũng phải được tính đến khi xác định u2(Vs) và u2(b).
VÍ DỤ 2: Trong ví dụ ở Chú thích 1 của 5.2.2, để phép hiệu chuẩn của từng điện trở được thể hiện bằng Ri = aiRs, với u(ai) là độ không đảm bảo chuẩn của tỉ số đo được ai như thu được từ quan trắc lặp lại. Hơn nữa, cho ai » 1 đối với từng điện trở và cho u(ai) về cơ bản là như nhau đối với từng phép hiệu chuẩn sao cho u(ai) » u(a). Khi đó, phương trình (F.1) và (F.2) tạo ra ![]() và u(Ri,Rj) = u2(Rs). Điều này gợi ý thông qua phương trình (14) trong 5.2.2 là hệ số tương quan của hai điện trở bất kỳ (i # j) là:
và u(Ri,Rj) = u2(Rs). Điều này gợi ý thông qua phương trình (14) trong 5.2.2 là hệ số tương quan của hai điện trở bất kỳ (i # j) là:
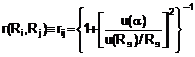
Vì u(Rs)/Rs = 10-4, nếu u(a) = 100 x 10-6, rij = 0,5; nếu u(a) = 10 x 10-6, rij = 0,990; và nếu u(a) = 1 x 10-6, rij » 1,000. Do đó u(a) -> 0, rij -> 1 và u(Ri) -> u(Rs).
CHÚ THÍCH: Nói chung, trong phép hiệu chuẩn so sánh như ví dụ này, các giá trị ước lượng được của đối tượng được hiệu chuẩn là tương quan, với độ tương quan phụ thuộc vào tỉ số độ không đảm bảo của so sánh với độ không đảm bảo của chuẩn chính. Thường xảy ra trong thực tế, khi độ không đảm bảo của phép so sánh là không đáng kể so với độ không đảm bảo của chuẩn, thì hệ số tương quan bằng +1 và độ không đảm bảo của từng đối tượng được hiệu chuẩn bằng độ không đảm bảo chuẩn.
F.1.2.4. Sự cần thiết của việc đưa vào hiệp phương sai u(xi,xj) có thể bỏ qua nếu tập hợp ban đầu các đại lượng đầu vào X1, X2, …, XN mà đại lượng đo Y phụ thuộc [xem phương trình (1) trong 4.1] được định nghĩa lại theo cách để gộp vào như đại lượng đầu vào độc lập bổ sung các đại lượng Ql đó chung cho nhiều Xi ban đầu. (Có thể cần thực hiện các phép đo bổ sung để thiết lập đầy đủ mối quan hệ giữa Ql và Xi bị ảnh hưởng). Tuy nhiên, trong một số tình huống giữ lại hiệp phương sai có thể thuận tiện hơn là tăng số lượng đại lượng đầu vào. Quá trình tương tự có thể được thực hiện trên hiệp phương sai quan trắc được của các quan trắc lặp lại đồng thời [xem phương trình (17) trong 5.2.3)] nhưng việc xác định các đại lượng đầu vào bổ sung phù hợp thường đặc biệt và phi vật lý.
VÍ DỤ; Trong ví dụ 1 của F.1.2.3, nếu biểu thức của I và t theo Rs được đưa vào biểu thức cho P, thì kết quả là:
![]()
Và sự tương quan giữa I và t tránh được khi thay thế đại lượng đầu vào I và t bằng đại lượng Vs, Rs và b. Vì các đại lượng này không tương quan nên phương sai của P có thể thu được từ phương trình (10) tron 5.1.2.
F.2. Các thành phần được đánh giá bằng cách khác: Đánh giá độ không đảm bảo chuẩn Loại B.
F.2.1. Sự cần thiết của đánh giá Loại B
Nếu phòng thí nghiệm đo lường có thời gian và nguồn lực vô hạn thì có thể tiến hành một nghiên cứu thống kê đầy đủ mọi nguyên nhân có thể biết của độ không đảm bảo, ví dụ, bằng cách sử dụng nhiều kiểu và loại phương tiện đo khác nhau, phương pháp đo khác nhau, cách áp dụng phương pháp khác nhau và phép tính gần đúng khác nhau trong các mô hình đo lý thuyết. Khi đó, độ không đảm bảo gắn với tất cả các nguyên nhân này có thể được đánh giá bằng phân tích thống kê các dãy quan trắc và độ không đảm bảo của từng nguyên nhân được đặc trưng bằng độ lệch chuẩn được đánh giá thống kê. Nói cách khác, tất cả thành phần của độ không đảm bảo thu được từ đánh giá Loại A. Vì sự nghiên cứu như vậy không có tính thực tiễn về kinh tế nên nhiều thành phần độ không đảm bảo phải được đánh giá bằng cách khác bất kỳ có tính thực tiễn.
F.2.2. Phân bố xác định theo toán học
F.2.2.1. Độ phân giải của chỉ thị hiện số
Một nguồn của độ không đảm bảo của phương tiện hiện số là độ phân giải của bộ chỉ thị. Ví dụ, thậm chí nếu số chỉ lặp lại đều giống nhau thì độ không đảm bảo của phép đo có thể quy cho độ lặp lại không phải bằng “không”, ví có dải tín hiệu đầu vào với phương tiện mở rộng khoảng đã biết để cho cùng một số chỉ. Nếu độ phân giải của bộ chỉ thị là dx, thì giá trị của kích thích tạo ra số chỉ đã cho X có thể nằm ở bất kỳ đâu với xác suất như nhau trong khoảng X – dx/2 đến X + dx/2. Do đó, sự kích thích được mô tả bằng phân bố xác suất chữ nhật (xem 4.3.7 và 4.4.5) có độ rộng dx với phương sai u2 = (dx)2/12, nghĩa là độ không đảm bảo chuẩn u = 0,29dx với mọi số chỉ.
Do đó, phương tiện cân với bộ hiển thị có chữ số có nghĩa nhỏ nhất là 1 g có phương sai do độ phân giải của phương tiện u2 = (1/12)g2 và độ không đảm bảo chuẩn u = (1/![]() )g = 0,29g
)g = 0,29g
F.2.2.2. Hiện tượng trễ
Kiểu trễ nhất định có thể gây ra một loại độ không đảm bảo tương tự. Số chỉ của phương tiện có thể khác nhau một lượng cố định và biết được tùy theo giá trị đọc liên tiếp dù tăng lên hay giảm xuống. Người vận hành có kinh nghiệm sẽ ghi lại hướng của các giá trị đọc liên tiếp và thực hiện hiệu chính thích hợp. Nhưng hướng của hiện tượng trễ không phải luôn quan sát được: có thể có dao động ẩn trong phương tiện quanh điểm cân bằng sao cho số chỉ phụ thuộc vào hướng mà từ đó điểm đó được tiếp cận cuối cùng. Nếu phạm vi của giá trị đọc có thể từ nguyên nhân đó là dx thì phương sai lại bằng u2 = (dx)2/12 và độ không đảm bảo chuẩn do trễ bằng u = 0,29dx.
F.2.2.3. Số học chính xác hữu hạn
Việc làm tròn lên hoặc bỏ bớt các chữ số xảy ra trong phép rút gọn dữ liệu tự động bằng máy tính cũng có thể là nguồn của độ không đảm bảo. Ví dụ, xét máy tính với độ dài từ 16 bít. Nếu trong quá trình tính toán, số có độ dài từ này bị trừ từ số khác nó chỉ sai khác ở bít thứ 16, thì chỉ một bit có nghĩa còn lại. Biến cố này có thể xảy ra trong sự đánh giá thuật toán “thiếu điều kiện” và chúng có thể khó dự đoán. Có thể thu được sự xác định thực nghiệm độ không đảm bảo bằng cách tăng đại lượng đầu vào quan trọng nhất cho tính toán (thường có một đại lượng tỉ lệ thuận với độ lớn của đại lượng đầu ra) bằng gia số nhỏ tới khi đại lượng đầu ra thay đổi; sự thay đổi nhỏ nhất của đại lượng đầu ra có thể thu được bằng cách này có thể lấy làm thước đo độ không đảm bảo; nếu nó là dx thì phương sai là u2 = (dx)2 / 12 và u = 0,29dx.
CHÚ THÍCH: Ta có thể kiểm tra việc đánh giá độ không đảm bảo bằng cách so sánh kết quả tính toán được thực hiện trên máy tính có độ dài từ hữu hạn với kết quả của cùng một tính toán được thực hiện trên máy có độ dài từ dài hơn đáng kể.
F.2.3. Giá trị đầu vào được đưa vào
F.2.3.1. Giá trị được đưa vào đối với đại lượng đầu vào là một giá trị, chưa được ước lượng trong phép đo đã cho nhưng đã thu được ở nguồn khác như kết quả của sự đánh giá độc lập. Giá trị được đưa vào này thường kèm theo một tuyên bố về độ không đảm bảo. Ví dụ, độ không đảm bảo có thể được đưa ra như độ lệch chuẩn, bội số của độ lệch chuẩn hoặc nửa độ rộng của khoảng có mức tin cậy được công bố. Các biên trên và dưới có thể được đưa ra hoặc không có thông tin về độ không đảm bảo có thể được cung cấp. Trong trường hợp sau, người sử dụng giá trị phải dùng chính sự hiểu biết của mình về độ lớn hợp lý của độ không đảm bảo, đưa ra bản chất của đại lượng, độ tin cậy về nguồn gốc, độ không đảm bảo thu được trong thực hành cho các đại lượng này …
CHÚ THÍCH: Thảo luận về độ không đảm bảo của các đại lượng đầu vào được kể đến trong điều này về đánh giá độ không đảm bảo chuẩn Loại B để thuận tiện; độ không đảm bảo của đại lượng này có thể bao gồm thành phần thu được từ đánh giá Loại A hoặc thành phần thu được từ đánh giá Loại A và Loại b. Do không cần phân biệt các thành phần được đánh giá bằng hai phương pháp khác nhau để tính độ không đảm bảo tổng hợp nên không cần biết thành phần độ không đảm bảo của đại lượng được đưa vào.
F.2.3.2. Một số phòng hiệu chuẩn đã chấp nhận thông lệ thể hiện “độ không đảm bảo” theo giới hạn trên và dưới xác định khoảng có mức mức tin cậy “tối thiểu”, ví dụ, “ít nhất” là 95%. Đây có thể được coi là ví dụ của việc gọi là độ không đảm bảo “an toàn” (xem E.1.2) và không thể chuyển thành độ không đảm bảo chuẩn mà không hiểu về cách tính toán. Nếu thông tin đầy đủ được đưa ra, có thể tính toán lại theo các nguyên tắc của tiêu chuẩn này; mặt khác sự đánh giá độc lập độ không đảm bảo phải được tiến hành bằng mọi cách có sẵn.
F.2.3.3. Một số độ không đảm bảo được đưa ra chỉ đơn giản là giá trị biên lớn nhất mà tất cả giá trị của đại lượng đều nằm trong đó. Đó là thực tế chung để giả định rằng tất cả giá trị nằm trong các giá trị biên đó là có xác suất như nhau (phân bố xác suất hình chữ nhật), nhưng phân bố như thế không cần được giả định nếu có lý do để kỳ vọng các giá trị ở trong nhưng gần biên ít khả năng hơn giá trị gần tâm của các giá trị biên. Phân bố chữ nhật của nửa độ rộng a có phương sai a2/3; phân bố chuẩn đối với a đó bằng nửa độ rộng của khoảng có mức tin cậy 99,73% có phương sai a2/9. Nên thận trọng khi chấp nhận thỏa hiệp giữa các giá trị, ví dụ, bằng cách giả định phân bố tam giác cho chúng với phương sai bằng a2/6 (xem 4.3.9 và 4.4.6)
F.2.4. Giá trị đầu vào đo được
F.2.4.1. Quan trắc đơn, phương tiện đã được hiệu chuẩn
Nếu ước lượng đại lượng đầu vào đã thu được từ quan trắc đơn bằng phương tiện đo cụ thể đã được hiệu chuẩn dựa vào chuẩn có độ không đảm bảo nhỏ, thì độ không đảm bảo của ước lượng chủ yếu là độ lặp lại. Phương sai của phép đo lặp lại bởi phương tiện có thể thu được ở thời điểm sớm hơn, không nhất thiết ở cùng giá trị đọc nhưng đủ gần để có ích và có khả năng giả định phương sai là có thể áp dụng vào giá trị đầu vào đang đề cập. Nếu không có sẵn thông tin như vậy thì phải tiến hành ước lượng dựa trên tính chất của dụng cụ hoặc phương tiện đo, phương sai đã biết của phương tiện khác có cấu trúc tương tự, .v.v…
F.2.4.2. Quan trắc đơn, phương tiện đã được kiểm định
Không phải tất cả phương tiện đo đều kèm giấy chứng nhận hiệu chuẩn hoặc đường cong hiệu chuẩn. Tuy nhiên, hầu hết phương tiện đo được xây dựng theo tiêu chuẩn viết sẵn và được kiểm định, bởi nhà sản xuất hoặc cơ quan có thẩm quyền độc lập, để phù hợp với tiêu chuẩn đó. Thông thường tiêu chuẩn có các yêu cầu đo lường, thường theo hình thức “sai số cho phép lớn nhất” mà phương tiện được yêu cầu phù hợp.
Sự phù hợp của phương tiện với các yêu cầu này được xác định bằng cách so sánh với phương tiện chuẩn mà độ không đảm bảo cho phép lớn nhất của nó thường được quy định trong tiêu chuẩn. Độ không đảm bảo này khi đó là thành phần độ không đảm bảo của phương tiện đã được kiểm định.
Nếu không biết về đặc trưng đường cong sai số của phương tiện đã được kiểm định thì phải giả định có một xác suất như nhau để sai số có bất kỳ giá trị trong giới hạn cho phép, nghĩa là, phân bố xác suất hình chữ nhật. Tuy nhiên, một số loại phương tiện có đường cong đặc tính sao cho sai số, ví dụ, gần như luôn dương trong một phần của phạm vi đo và âm trong các phần khác. Đôi khi thông tin như trên có thể được suy ra từ nghiên cứu tiêu chuẩn được biên soạn.
F.2.4.3. Đại lượng được kiểm soát
Phép đo thường thực hiện dưới điều kiện quy chiếu được kiểm soát với giả định được duy trì không đổi trong suốt quá trình của dãy các phép đo. Ví dụ, phép đo có thể được tiến hành trên mẫu trong bể dầu khuấy có nhiệt độ được kiểm soát bằng bộ điều nhiệt. Nhiệt độ của bể có thể được đo tại thời điểm của từng phép đo trên mẫu nhưng nếu nhiệt độ của bể theo chu kỳ thì nhiệt độ tức thời của mẫu có thể không phải là nhiệt độ được chỉ thị bởi nhiệt kế trong bể. Sự tính toán dao động nhiệt độ của mẫu dựa trên lý thuyết truyền nhiệt, và phương sai, nằm ngoài phạm vi của tiêu chuẩn này nhưng nó phải bắt đầu từ chu kỳ nhiệt độ đã biết hoặc được giả định đối với bể. Chu kỳ đó có thể được quan trắc bằng cặp nhiệt điện tốt và bộ ghi nhiệt độ, nhưng nhược điểm là phép tính gần đúng của nó có thể được suy luận từ sự hiểu biết về bản chất của việc kiểm soát.
F.2.4.4. Phân bố bất đối xứng của các giá trị có thể có
Có những trường hợp khi tất cả các giá trị có thể có của đại lượng nằm về một phía của giá trị giới hạn đơn. Ví dụ, khi đo chiều cao thẳng đứng cố định h (đại lượng đo) của cột chất lỏng trong áp kế, trục của phương tiện đo độ cao có thể lệch khỏi hướng thẳng đứng một góc nhỏ b. Khoảng cách l được xác định bằng phương tiện sẽ luôn lớn hơn h; không thể có giá trị nhỏ hơn h. Điều này là vì h bằng hình chiếu lcosb, dẫn đến l = h/cosb và tất cả giá trị của cosb nhỏ hơn một; không thể có giá trị nào lớn hơn một. Cái gọi là “sai số cosin” này cũng có thể xuất hiện theo hướng hình chiếu h’cosb của đại lượng đo h’ bằng khoảng cách l quan trắc được, nghĩa là l = h’cosb, và khoảng cách quan trắc được luôn nhỏ hơn đại lượng đo.
Néu biến mới d = 1 – cosb được đưa ra, giả sử b » 0 hoặc d << 1 như trường hợp thông thường trong thực tiễn, thì hai tình huống khác nhau là:
![]()
Ở đây ![]() , ước lượng tốt nhất của
, ước lượng tốt nhất của ![]() , là trung bình cộng hoặc trung bình của n quan trắc lặp lại độc lập
, là trung bình cộng hoặc trung bình của n quan trắc lặp lại độc lập ![]() của
của ![]() với phương sai ước lượng u2(
với phương sai ước lượng u2(![]() ) [xem phương trình (3) và (5) trong 4.2]. Do đó, từ phương trình (F.3a) và (F.3b) để thu được ước lượng của h hoặc h’ yêu cầu ước lượng của thừa số hiệu chính d trong khi để nhận được độ không đảm bảo chuẩn tổng hợp của ước lượng của h hoặc h’ đòi hỏi có u2(d), phương sai ước lượng của d. Cụ thể hơn, việc áp dụng phương trình (10) trong 5.1.2 cho phương trình (F.3a) và (F.3b) được
) [xem phương trình (3) và (5) trong 4.2]. Do đó, từ phương trình (F.3a) và (F.3b) để thu được ước lượng của h hoặc h’ yêu cầu ước lượng của thừa số hiệu chính d trong khi để nhận được độ không đảm bảo chuẩn tổng hợp của ước lượng của h hoặc h’ đòi hỏi có u2(d), phương sai ước lượng của d. Cụ thể hơn, việc áp dụng phương trình (10) trong 5.1.2 cho phương trình (F.3a) và (F.3b) được ![]() và
và ![]() (có dấu – và +, tương ứng)
(có dấu – và +, tương ứng)

Để thu được ước lượng của giá trị kỳ vọng của d và phương sai của d, giả định rằng của phương tiện được sử dụng để đo chiều cao của cột chất lỏng trong áp kế bắt buộc để cố định trong mặt phẳng thẳng đứng và phân bố các giá trị của góc nghiêng b quanh giá trị không được kỳ vọng là phân bố chuẩn với phương sai s2. Mặc dù b có thể có cả giá trị dương và âm nhưng d = 1 – cosb dương với mọi giá trị b. Nếu sự lệch trục của trục phương tiện đo được giả định là không bắt buộc thì hướng của trục có thể thay đổi theo góc khối do cũng có khả năng lệch trục trong góc phương vị nhưng khi đó b luôn là góc dương.
Trong trường hợp bắt buộc hoặc một chiều, phần tử xác suất p(b)db (C.2.5, chú thích) tỉ lệ với {exp[-b2/(2s2)]}db; trong trường hợp không bắt buộc hoặc hai chiều, phần tử xác suất tỉ lệ với {exp[-b2/(2s2)]}sinbdb. Hàm mật độ xác suất p(d) trong hai trường hợp này là biểu thức cần có để xác định kỳ vọng và phương sai của d để sử dụng trong phương trình (F.3) và (F.4). Chúng có thể dễ dàng thu được từ các phần tử xác suất này vì góc b có thể giả định là nhỏ, và do đó d = 1 – cosb và sinb có thể khai triển với bậc thấp nhất theo b. Điều này dẫn đến d » b2/2, sinb » b = ![]() và
và ![]() . Khi đó, hàm mật độ xác suất bằng:
. Khi đó, hàm mật độ xác suất bằng:
![]() (F.5a)
(F.5a)
Cho trường hợp một chiều
![]() (F.5b)
(F.5b)
Cho trường hợp hai chiều
Trong đó: ![]()
Phương trình (F.5a) và (F.5b), chỉ ra rằng hầu hết giá trị có thể có của hiệu chính d trong hai trường hợp bằng “không”, đưa ra trong trường hợp một chiều E(d) = s2/2 và var(d) = s4/2 đối với kỳ vọng và phương sai của d; trong trường hợp hai chiều E(d) = s2 và var(d) = s4. Khi đó phương trình (F.3a), (F.3b) và (F.4b) trở thành:
![]() (F.6a)
(F.6a)
![]() (F.6b)
(F.6b)
![]() (F.6c)
(F.6c)
Trong đó d là bậc (d = 1 hoặc 2) và u(b) là độ không đảm bảo chuẩn của góc b, được lấy làm ước lượng tốt nhất của độ lệch chuẩn s của phân bố chuẩn được giả định và được đánh giá từ tất cả thông tin có sẵn liên quan đến phép đo (đánh giá Loại B). Đây là ví dụ về trường hợp khi ước lượng của giá trị đại lượng đo phụ thuộc vào độ không đảm bảo của đại lượng đầu vào.
Mặc dù phương trình từ (F.6a) đến (F.6c) đặc trưng cho phân bố chuẩn, việc phân tích có thể tiến hành với giả định phân bố khác cho b. Ví dụ, nếu giả định đối với b là phân bố chữ nhật đối xứng với biên trên và dưới +bo và –bo trong trường hợp một chiều, +bo và 0 trong trường hợp hai chiều, ![]() và
và ![]() trong một chiều;
trong một chiều; ![]() và
và ![]() trong hai chiều.
trong hai chiều.
CHÚ THÍCH: Đây là tình huống sự khai triển của hàm Y = f(X1, X2, …, XN) theo chuỗi Taylor bậc một để thu được ![]() , phương trình (10) trong 5.1.2 là không đầy đủ vì tính phi tuyến của f:
, phương trình (10) trong 5.1.2 là không đầy đủ vì tính phi tuyến của f: ![]() (xem Chú thích của 5.1.2 và H.2.4). Mặc dù phân tích có thể được thực hiện đầy đủ với các số hạng của b nhưng đưa ra biến d sẽ làm đơn giản vấn đề.
(xem Chú thích của 5.1.2 và H.2.4). Mặc dù phân tích có thể được thực hiện đầy đủ với các số hạng của b nhưng đưa ra biến d sẽ làm đơn giản vấn đề.
Một ví dụ khác về tình huống khi tất cả giá trị có thể có của đại lượng nằm về một phía của giá trị giới hạn đơn là việc xác định bằng sự chuẩn độ nồng độ thành phần trong dung dịch trong đó điểm cuối được biểu thị bằng sự kích hoạt tín hiệu; lượng thuốc thử thêm vào luôn nhiều hơn cần thiết để kích hoạt tín hiệu; không bao giờ ít hơn. Lượng dư được chuẩn độ vượt quá điểm giới hạn là biến cần thiết trong phép rút gọn dữ liệu và thủ tục trong trường hợp này (và tương tự) là để giả định phân bố xác suất phù hợp cho lượng vượt quá và sử dụng nó để thu được giá trị kỳ vọng của lượng vượt quá và phương sai của nó.
VÍ DỤ: Nếu phân bố chữ nhật của biên dưới “không” và biên trên Co được giả định đối với lượng vượt quá z thì giá trị kỳ vọng của lượng dư là Co/2 với phương sai kèm theo ![]() . Nếu hàm mật độ xác suất của lượng vượt quá được lấy như của phân bố chuẩn với 0 £ z < ¥, nghĩa là,
. Nếu hàm mật độ xác suất của lượng vượt quá được lấy như của phân bố chuẩn với 0 £ z < ¥, nghĩa là, ![]() , khi đó giá trị mong muốn bằng
, khi đó giá trị mong muốn bằng ![]() với phương sai s2(1 – 2/p).
với phương sai s2(1 – 2/p).
F.2.4.5. Độ không đảm bảo khi không áp dụng sự hiệu chính từ đường cong hiệu chuẩn
Chú thích của 6.3.1 thảo luận trường hợp số hiệu chính đã biết b đối với ảnh hưởng hệ thống quan trọng không được áp dụng với kết quả báo cáo của phép đo nhưng thay vào đó được tính đến bằng cách mở rộng “độ không đảm bảo” được ấn định cho kết quả. Ví dụ là sự thay thế độ không đảm bảo mở rộng U bằng U + b, trong đó U là độ không đảm bảo mở rộng thu được dưới giả định b = 0. Thực tế này đôi khi được tuân theo trong tình huống khi tất cả điều kiện sau đây áp dụng: đại lượng đo Y được xác định nhờ dãy giá trị tham số t, như trong trường hợp đường cong hiệu chuẩn đối với cảm biến nhiệt độ; U và b cũng phụ thuộc vào t; và chỉ giá trị đơn của “độ không đảm bảo” được đưa ra cho tất cả ước lượng y(t) của đại lượng đo trên dãy giá trị dương của t. Trong tình huống như vậy kết quả đo đó thường được báo cáo là Y(t) = y(t) ± [Umax + bmax], trong đó chỉ số dưới “max” chỉ giá trị lớn nhất của U và giá trị lớn nhất của sự hiệu chính đã biết b trên toàn dãy giá trị t đã sử dụng.
Mặc dù tiêu chuẩn này khuyến nghị rằng sự hiệu chính được áp dụng cho kết quả đo đối với ảnh hưởng hệ thống quan trọng, nhưng điều này không phải luôn khả thi trong tình huống như vậy vì chi phí không thể chấp nhận cho việc tính toán và áp dụng sự hiệu chính riêng lẻ và trong việc tính toán và sử dụng độ không đảm bảo riêng lẻ cho từng giá trị y(t).
Cách tiếp cận tương đối đơn giản cho vấn đề này phù hợp với nguyên tắc của tiêu chuẩn này như sau:
Tính số hiệu chính trung bình đơn b từ:
![]() (F.7a)
(F.7a)
Trong đó t1 và t2 xác định dãy quan tâm của tham số t và lấy ước lượng tốt nhất của Y(t) là y'(t) = y(t) +![]() , trong đó y(t) là ước lượng chưa được hiệu chính tốt nhất của Y(t). Phương sai kèm theo số hiệu chính trung bình
, trong đó y(t) là ước lượng chưa được hiệu chính tốt nhất của Y(t). Phương sai kèm theo số hiệu chính trung bình ![]() trên toàn dãy quan trắc được cho bằng:
trên toàn dãy quan trắc được cho bằng:
![]() (F.7b)
(F.7b)
Không tính đến độ không đảm bảo của sự xác định thực tế số hiệu chính b(t). Phương sai trung bình của số hiệu chính b(t) do sự xác định thực tế được cho bằng:
![]() (F.7c)
(F.7c)
Trong đó u2[b(t)] là phương sai của số hiệu chính b(t). Tương tự, phương sai trung bình của y(t) xuất hiện từ tất cả các nguồn độ không đảm bảo ngoài số hiệu chính b(t) thu được từ:
![]() (F.7d)
(F.7d)
Trong đó u2[y(t)] là phương sai của y(t) do tất cả các nguồn độ không đảm bảo ngoài b(t). Giá trị đơn của độ không đảm bảo chuẩn được sử dụng đối với tất cả ước lượng y'(t) = y(t) + ![]() của đại lượng đo Y(t) khi đó bằng dương căn bậc hai của:
của đại lượng đo Y(t) khi đó bằng dương căn bậc hai của:
![]() (F.7e)
(F.7e)
Độ không đảm bảo mở rộng U có thể thu được bằng cách nhân uc(y’) với hệ số phủ được chọn phù hợp k, U = kuc(y’), dẫn tới Y(t) = y'(t) ± U = y(t) + b ± U. Tuy nhiên, việc sử dụng cùng một số hiệu chính trung bình cho tất cả giá trị t mà không phải là số hiệu chính phù hợp đối với từng giá trị t phải được thừa nhận và công bố rõ ràng được đưa ra khi trình bày U.
F.2.5. Độ không đảm bảo của phương pháp đo
F.2.5.1. Có thể thành phần của độ không đảm bảo khó đánh giá nhất là thành phần gắn với phương pháp đo, đặc biệt, nếu việc áp dụng phương pháp đó được chỉ ra cho kết quả ít thay đổi hơn kết quả của phương pháp khác đã biết. Nhưng có vẻ có các phương pháp khác, một số vẫn chưa được biết đến hoặc không thực tế theo cách nào đó có thể mang lại các kết quả khác nhau một cách hệ thống, có cơ sở dường như là ngang nhau. Điều này ám chỉ phân bố xác suất tiên nghiệm, không phải phân bố mà từ đó mẫu có thể được lấy dễ dàng và xử lý thống kê. Do đó, mặc dù độ không đảm bảo của phương pháp có thể là độ không đảm bảo chính nhưng chỉ thông tin thường có sẵn cho việc đánh giá độ không đảm bảo chuẩn mới là kiến thức hiện có về lĩnh vực vật lý. (Xem thêm E.4.4)
CHÚ THÍCH: Việc xác định cùng đại lượng đo bằng phương pháp khác nhau, trong cùng phòng thí nghiệm hay các phòng thí nghiệm khác nhau, hoặc bằng cùng phương pháp trong các phòng thí nghiệm khác nhau, thường có thể cung cấp thông tin có giá trị về độ không đảm bảo có thể quy cho phương pháp cụ thể. Nói chung, sự trao đổi chuẩn đo lường hoặc mẫu chuẩn giữa các phòng thí nghiệm đối với phép đo độc lập là cách hiệu quả để đánh giá độ tin cậy của việc đánh giá độ không đảm bảo và xác định ảnh hưởng hệ thống chưa được thừa nhận trước đây.
F.2.6. Độ không đảm bảo của mẫu
F.2.6.1. Nhiều phép đo bao gồm việc so sánh đối tượng chưa biết với chuẩn đã biết có đặc trưng tương tự để hiệu chuẩn đối tượng chưa biết. Ví dụ bao gồm các can chuẩn, nhiệt kế, bộ quả cân, điện trở và vật liệu tinh khiết cao. Trong hầu hết các trường hợp như vậy, phương pháp đo không ảnh hưởng đặc biệt tới, hoặc chịu ảnh hưởng bất lợi bởi, việc thu thập mẫu (nghĩa là, sự không biết cụ thể được hiệu chuẩn), việc xử lý mẫu, hoặc ảnh hưởng của đại lượng tác động môi trường khác nhau vì sự không biết và chuẩn thường phản ứng tương tự (và thường có thể dự đoán được) với các biến đó.
F.2.6.2. Trong một số tình huống đo thực tế, việc lấy mẫu và xử lý mẫu thử đóng vai trò lớn hơn nhiều. Đây thường là trường hợp phân tích hóa học vật liệu tự nhiên. Không giống vật liệu nhân tạo, có thể có tính đồng nhất đã được chứng minh ở mức cần thiết đối với phép đo, vật liệu tự nhiên thường rất không đồng nhất. Tính không đồng nhất này dẫn tới hai thành phần độ không đảm bảo bổ sung. Việc đánh giá thành phần thứ nhất yêu cầu xác định mẫu được chọn đại diện cho vật liệu ban đầu thích hợp đến đâu để phân tích. Việc đánh giá thành phần thứ hai yêu cầu xác định phạm vi mà thành phần (không được phân tích) thứ cấp ảnh hưởng đến phép đo và chúng được xử lý bằng phương pháp đo thích hợp đến đâu.
F.2.6.3. Trong một số trường hợp, sự thiết kế cẩn thận thực nghiệm làm cho có khả năng đánh giá thống kê độ không đảm bảo do mẫu (xem H.5 và H.5.3.2). Tuy nhiên, thông thường, đặc biệt khi tác động của đại lượng ảnh hưởng môi trường lên mẫu là đáng kể, kỹ năng và sự hiểu biết về phân tích nhận được từ thực nghiệm và tất cả thông tin có sẵn là cần thiết cho việc đánh giá độ không đảm bảo.
PHỤ LỤC G
(tham khảo)
BẬC TỰ DO VÀ MỨC TIN CẬY
G.1. Giới thiệu
G.1.1. Phụ lục này tập trung vào vấn đề chung về việc thu được từ ước lượng y của đại lượng đo Y và từ độ không đảm bảo chuẩn tổng hợp uc(y) của đại lượng đó, độ không đảm bảo mở rộng Up = kpuc(y) xác định khoảng y – Up £ Y £ y + Up có xác suất phủ cao, được quy định hoặc mức tin cậy p. Do đó, nó giải quyết vấn đề xác định hệ số phủ kp mang lại khoảng kết quả đo y có thể mở rộng để chứa phần lớn p đã được quy định của phân bố giá trị có thể quy hợp lý cho đại lượng đo Y (xem Điều 6).
G.1.2. Trong hầu hết tính huống đo thực tế, việc tính toán khoảng có mức tin cậy được quy định – thực chất là sự ước lượng hầu hết thành phần độ không đảm bảo riêng lẻ trong các tình huống đó – chỉ là gần đúng tốt nhất. Thậm chí độ lệch chuẩn thực nghiệm trung bình của 30 quan trắc lặp lại đại lượng được mô tả bằng phân bố chuẩn có độ không đảm bảo bằng khoảng 13% (xem Bảng E.1 trong Phụ lục E).
Trong hầu hết các trường hợp, không có nghĩa khi phân biệt giữa, ví dụ, khoảng có mức tin cậy 95% (1 trong 20 cơ hội là giá trị của đại lượng đo Y nằm ngoài khoảng) và 94% hoặc 96% khoảng (1 trong 17 và 20 cơ hội, tương ứng). Khoảng hợp lý thu được với mức tin cậy 99% (1 trong 100 cơ hội) và cao hơn là đặc biệt khó, thậm chí nếu giả định rằng không có ảnh hưởng hệ thống nào bị bỏ sót, vì quá ít thông tin có sẵn về phần chia x nhất hoặc “đuôi” của phân bố xác suất của đại lượng đầu vào.
G.1.3. Để thu được giá trị hệ số phủ kp tạo ra khoảng tương ứng với mức tin cậy quy định p cần hiểu biết chi tiết về phân bố xác suất đặc trưng bởi kết quả đo và độ không đảm bảo chuẩn tổng hợp. Ví dụ, đối với đại lượng z được mô tả bởi phân bố chuẩn có kỳ vọng mz và độ lệch chuẩn s, giá trị kp tạo ra khoảng mz ± kps chứa phần p của phân bố, và do đó có xác suất phủ hoặc mức tin cậy p, có thể tính được dễ dàng. Một số ví dụ được cho trong Bảng G.1.
Bảng G.1 – Giá trị hệ số phủ kp tạo ra khoảng có mức tin cậy p giả định phân bố chuẩn
|
Mức tin cậy p |
Hệ số phủ kp |
|
68,27 90 95 95,45 99 99,73 |
1 1,645 1,960 2 2,576 3 |
CHÚ THÍCH: Ngược lại, nếu z được mô tả bằng phân bố xác suất hình chữ nhật có kỳ vọng mz va độ lệch chuẩn ![]() , trong đó a bằng nửa độ rộng của phân bố, mức tin cậy p bằng 57,74% đối với kp = 1; 95% đối với kp = 1,65; 99% đối với kp = 1,71 và 100% đối với kp ³
, trong đó a bằng nửa độ rộng của phân bố, mức tin cậy p bằng 57,74% đối với kp = 1; 95% đối với kp = 1,65; 99% đối với kp = 1,71 và 100% đối với kp ³ ![]() » 1,73; phân bố chữ nhật “hẹp hơn” phân bố chuẩn theo nghĩa phạm vi có hạn và không có “đuôi”.
» 1,73; phân bố chữ nhật “hẹp hơn” phân bố chuẩn theo nghĩa phạm vi có hạn và không có “đuôi”.
G.1.4. Nếu biết phân bố xác suất của đại lượng đầu vào X1, X2, …, XN mà đại lượng đo phụ thuộc vào [kỳ vọng, phương sai và mô men bậc cao hơn của chúng (xem C.2.13 và C.2.22) nếu phân bố không phải là phân bố chuẩn] và nếu Y là hàm tuyến tính của đại lượng đầu vào, Y = c1X1 + c2X2 + … + cNXN, thì phân bố xác suất của Y có thể thu được bằng tích chập các phân bố xác suất riêng rẽ [10]. Giá trị kp tạo ra khoảng tương ứng với mức tin cậy quy định p khi đó có thể tính được từ phân bố chấp nhận được.
G.1.5. Nếu mối quan hệ hàm số giữa Y và đại lượng đầu vào không tuyến tính và sự mở rộng chuỗi Taylor bậc nhất của mối quan hệ đó không phải là phép tính gần đúng có thể chấp nhận được (xem 5.1.2 và 5.1.5) thì phân bố xác suất của Y không thể thu được bằng cách tích chập phân bố đại lượng đầu vào. Trong trường hợp đó, cần có phương pháp phân tích hoặc phương pháp số khác.
G.1.6. Trong thực tế, vì tham số đặc trưng cho phân bố xác suất của đại lượng đầu vào thường là các ước lượng, vì không thực tế khi kỳ vọng mức tin cậy gắn với khoảng đã cho có thể được biết chính xác và vì sự phức tạp của phân bố xác suất chập nên tích chập hiếm khi được thực hiện, nếu có, áp dụng khi các khoảng có mức tin cậy quy định cần được tính toán. Thay vào đó, phép tính gần đúng được sử dụng áp dụng lý thuyết giới hạn trung tâm.
G.2. Lý thuyết giới hạn trung tâm
G.2.1. Nếu Y = c1X1 + c2X2 + … + cNXN = ![]() và tất cả Xi được đặc trưng bằng phân bố chuẩn, phân bố chập thu được của Y cũng sẽ là chuẩn. Tuy nhiên, thậm chí nếu phân bố của Xi không chuẩn, phân bố của Y thường có thể được tính xấp xỉ bằng phân bố chuẩn nhờ lý thuyết giới hạn trung tâm. Định lý này tuyên bố phân bố của Y sẽ gần với chuẩn có kỳ vọng
và tất cả Xi được đặc trưng bằng phân bố chuẩn, phân bố chập thu được của Y cũng sẽ là chuẩn. Tuy nhiên, thậm chí nếu phân bố của Xi không chuẩn, phân bố của Y thường có thể được tính xấp xỉ bằng phân bố chuẩn nhờ lý thuyết giới hạn trung tâm. Định lý này tuyên bố phân bố của Y sẽ gần với chuẩn có kỳ vọng ![]() và phương sai
và phương sai ![]() , trong đó E(Xi) là kỳ vọng của Xi và
, trong đó E(Xi) là kỳ vọng của Xi và ![]() là phương sai của Xi, nếu Xi độc lập và
là phương sai của Xi, nếu Xi độc lập và ![]() lớn hơn nhiều so với bất kỳ thành phần riêng lẻ
lớn hơn nhiều so với bất kỳ thành phần riêng lẻ ![]() từ Xi không được phân bố chuẩn.
từ Xi không được phân bố chuẩn.
G.2.2. Lý thuyết giới hạn trung tâm có ý nghĩa vì nó chỉ ra vai trò rất quan trọng của phương sai của phân bố xác suất các đại lượng đầu vào, so với vai trò mô men cao hơn của phân bố đó, trong việc xác định mô hình của phân bố chập thu được của Y. Hơn nữa, nó hàm ý phân bố chập hội tụ về phân bố chuẩn khi số đại lượng đầu vào góp phần làm tăng s2(Y); sự hội tụ đó sẽ càng nhanh hơn khi các giá trị ![]() càng gần nhau hơn (tương tự trong thực tiễn với từng ước lượng đầu vào xi đóng góp độ không đảm bảo so sánh được độ không đảm bảo của ước lượng y của đại lượng đo Y); và các phân bố của Xi càng gần với phân bố chuẩn hơn, thì càng cần ít Xi hơn để tạo phân bố chuẩn đối với Y.
càng gần nhau hơn (tương tự trong thực tiễn với từng ước lượng đầu vào xi đóng góp độ không đảm bảo so sánh được độ không đảm bảo của ước lượng y của đại lượng đo Y); và các phân bố của Xi càng gần với phân bố chuẩn hơn, thì càng cần ít Xi hơn để tạo phân bố chuẩn đối với Y.
VÍ DỤ: Phân bố chữ nhật (xem 4.3.7 và 4.4.5) là một ví dụ về phân bố không chuẩn nhưng sự chấp của thậm chí ít ba phân bố có độ rộng bằng nhau đã là gần chuẩn. Nếu nửa độ rộng của từng trong ba phân bố là a thì phương sai của từng phân bố là a2/3, phương sai của phân bố chập là s2 = a2. Khoảng 95% và 99% của phân bố chập được xác định tương ứng bằng 1,937s và 2,379s, trong khi khoảng tương ứng đối với phân bố chuẩn có cùng độ lệch chuẩn s được xác định bằng 1,960s và 2,576s (xem Bảng G.1) [10].
CHÚ THÍCH 1: Với từng khoảng có mức tin cậy p lớn hơn khoảng 91,7%, giá trị của kp đối với phân bố chuẩn lớn hơn giá trị tương ứng đối với phân bố thu được từ tích chập bất kỳ số và cỡ phân bố chữ nhật nào.
CHÚ THÍCH 2: Theo lý thuyết giới hạn trung tâm, phân bố xác suất của trung bình cộng ![]() của n quan trắc qk của biến ngẫu nhiên q với kỳ vọng mq và độ lệch chuẩn hữu hạn s tiến gần đến phân bố chuẩn với trung bình mq và độ lệch chuẩn
của n quan trắc qk của biến ngẫu nhiên q với kỳ vọng mq và độ lệch chuẩn hữu hạn s tiến gần đến phân bố chuẩn với trung bình mq và độ lệch chuẩn ![]() khi n -> ¥, bất kể có thể là phân bố xác suất của q.
khi n -> ¥, bất kể có thể là phân bố xác suất của q.
G.2.3. Ý nghĩa thực hành của lý thuyết giới hạn trung tâm là khi có thể chứng minh rằng các yêu cầu của nó gần được đáp ứng, cụ thể, nếu độ không đảm bảo chuẩn tổng hợp uc(y) không bị chi phối bởi thành phần độ không đảm bảo chuẩn thu được từ đánh giá Loại A chỉ dựa trên số ít quan trắc hoặc thành phần độ không đảm bảo chuẩn thu được từ đánh giá Loại B trên cơ sở phân bố chữ nhật giả định, phép tính gần đúng đầu tiên hợp lý để tính độ không đảm bảo mở rộng Up = kpuc(y) cung cấp khoảng với mức tin cậy p là để sử dụng với kp một giá trị từ phân bố chuẩn. Các giá trị được sử dụng phổ biến nhất cho mục đích này được nêu trong Bảng G.1.
G.3. Phân bố t và bậc tự do
G.3.1. Để thu được phép tính gần đúng tốt hơn so với sử dụng đơn giản giá trị kp từ phân bố chuẩn như trong G.2.3, phải thừa nhận việc tính khoảng có mức tin cậy được quy định yêu cầu, không phải phân bố của biến [Y – E(Y)]/s(Y), mà là phân bố của biến (y – Y)/uc(y). Điều này là vì trong thực tế tất cả những cái thường có sẵn là y, ước lượng của Y như thu được từ ![]() , trong đó, xi là ước lượng của Xi; phương sai tổng hợp gắn với y,
, trong đó, xi là ước lượng của Xi; phương sai tổng hợp gắn với y, ![]() , được đánh giá từ
, được đánh giá từ ![]() , trong đó u(xi) là độ không đảm bảo chuẩn (độ lệch chuẩn ước lượng) của ước lượng xi.
, trong đó u(xi) là độ không đảm bảo chuẩn (độ lệch chuẩn ước lượng) của ước lượng xi.
CHÚ THÍCH: Nói đúng ra, trong biểu thức (y – Y)/uc(y), Y cần đọc là E(Y). Để đơn giản, sự phân biệt này chỉ thực hiện ở một vài chỗ trong tiêu chuẩn này. Nói chung, ký hiệu giống nhau được sử dụng cho đại lượng vật lý, biến ngẫu nhiên đại diện cho đại lượng đó và kỳ vọng của biến đó (xem 4.1.1, Chú thích).
G.3.2. Nếu z là biến ngẫu nhiên có phân bố chuẩn với kỳ vọng mz, độ lệch chuẩn s và ![]() là trung bình cộng của n quan trắc độc lập zk của z của s(
là trung bình cộng của n quan trắc độc lập zk của z của s(![]() ) là độ lệch chuẩn thực nghiệm của
) là độ lệch chuẩn thực nghiệm của ![]() [xem phương trình (3) và (5) trong 4.2], khi đó phân bố của biến t = (
[xem phương trình (3) và (5) trong 4.2], khi đó phân bố của biến t = (![]() – mz)/s(
– mz)/s(![]() ) là phân bố t hay phân bố Student (C.3.8) với v = n -1 bậc tự do.
) là phân bố t hay phân bố Student (C.3.8) với v = n -1 bậc tự do.
Do đó, nếu đại lượng đo Y đơn giản là đại lượng được phân bố chuẩn đơn lẻ X, Y = X, và nếu X được ước lượng bởi trung bình cộng ![]() của n quan trắc lặp lại độc lập Xk của X, với độ lệch chuẩn thực nghiệm của trung bình s(
của n quan trắc lặp lại độc lập Xk của X, với độ lệch chuẩn thực nghiệm của trung bình s(![]() ), thì ước lượng tốt nhất của Y là y =
), thì ước lượng tốt nhất của Y là y = ![]() và độ lệch chuẩn thực nghiệm của ước lượng đó là uc(y) = s(
và độ lệch chuẩn thực nghiệm của ước lượng đó là uc(y) = s(![]() ). Khi đó t = (
). Khi đó t = (![]() – mz)/s(
– mz)/s(![]() ) = (
) = (![]() – X)/s(
– X)/s(![]() ) = (y – Y)/uc(y) được phân bố theo phân bố t với:
) = (y – Y)/uc(y) được phân bố theo phân bố t với:
Pr(-tp(v) £ t £ tp(v)] = p (G.1a)
Hoặc
Pr[-tp(v) £ (y – Y)/uc(y) < tp(v)] = p (G.1b)
Có thể viết lại như sau:
Pr[y – tp(v)uc(y) £ Y £ y + tp(v)uc(y)] = p (G.1c)
Trong các biểu thức này, Pr[] nghĩa là “xác suất của” và thừa số -t, tp(v) là giá trị của t đối với giá trị đã cho của tham số v – bậc tự do (xem G.3.3) – như phần p của phân bố t được bao quanh bởi khoảng -tp(v) tới +tp(v). Do đó, độ không đảm bảo mở rộng
Up = kpuc(y) = tp(v)uc(y) (G.1d)
Xác định khoảng y – Up tới y + Up, viết ngắn gọn là Y = y ± Up, có thể được kỳ vọng chứa phần p của phân bố các giá trị có thể được gán hợp lý cho Y và p là xác suất phủ hoặc mức tin cậy của khoảng đó.
G.3.3. Bậc tự do v bằng n – 1 đối với một đại lượng được ước lượng bằng trung bình cộng của n quan trắc độc lập, như trong G.3.2. Nếu n quan trắc độc lập được sử dụng để xác định độ dốc và phần bị chặn của đường thẳng bằng phương pháp bình phương tối thiểu, thì bậc tự do của độ không đảm bảo chuẩn tương ứng là v = n -2. Đối với việc làm khớp bình phương tối thiểu của m tham số với n điểm dữ liệu, bậc tự do của độ không đảm bảo chuẩn của từng tham số là v = n – m. (Xem Tài liệu tham khảo [15] thảo luận kỹ hơn về bậc tự do.)
G.3.4. Giá trị được chọn của tp(v) với các giá trị khác nhau của v và các giá trị khác nhau của p được nêu trong Bảng G.2 ở cuối phụ lục này. Khi v -> ¥, phân bố t tiệm cận phân bố chuẩn và tp(v) » (1+2/v)1/2kp, ở đó trong biểu thức này kp là hệ số phủ yêu cầu để thu được một khoảng với mức tin cậy p đối với biến có phân bố chuẩn. Do đó giá trị tp(¥) trong Bảng G.2 đối với p đã cho bằng giá trị của kp trong Bảng G.1 đối với cùng một giá trị p.
CHÚ THÍCH; Thông thường, phân bố t được lập bảng theo các phân vị; nghĩa là, giá trị của phân vị t1-a được cho trước, trong đó 1-a chỉ xác suất tích lũy và mối quan hệ
![]()
Xác định phân vị, trong đó f là hàm mật độ xác suất của t. Do đó tp và t1-a có liên hệ bởi p = 1-2a . Ví dụ, giá trị của điểm phân vị t0,975, ứng với 1-a = 0,975 và a = 0,025 là giống như tp(v) đối với p = 0,95.
G.4. Bậc tự do hiệu dụng
G.4.1. Nói chung, phân bố t sẽ không mô tả phân bố của biến (y – Y)/uc(y) nếu ![]() là tổng của hai hay nhiều thành phần phương sai được ước lượng
là tổng của hai hay nhiều thành phần phương sai được ước lượng ![]() (xem 5.1.3), thậm chí nếu từng xi là ước lượng của đại lượng đầu vào có phân bố chuẩn Xi. Tuy nhiên, phân bố của biến đó có thể gần đúng bằng phân bố t có các bậc tự do hiệu dụng veff thu được từ công thức Welch-Satterthwaite [16], [17], [18].
(xem 5.1.3), thậm chí nếu từng xi là ước lượng của đại lượng đầu vào có phân bố chuẩn Xi. Tuy nhiên, phân bố của biến đó có thể gần đúng bằng phân bố t có các bậc tự do hiệu dụng veff thu được từ công thức Welch-Satterthwaite [16], [17], [18].
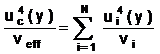 (G.2a)
(G.2a)
Hoặc
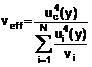 (G.2b)
(G.2b)
Với ![]() (G.2c)
(G.2c)
Trong đó ![]() (xem 5.1.3). Độ không đảm bảo mở rộng Up = kpuc(y) = tp(veff)uc(y) khi đó cho một khoảng Y = y ± Up có mức tin cậy gần đúng p.
(xem 5.1.3). Độ không đảm bảo mở rộng Up = kpuc(y) = tp(veff)uc(y) khi đó cho một khoảng Y = y ± Up có mức tin cậy gần đúng p.
CHÚ THÍCH 1: Nếu giá trị của veff thu được từ phương trình (G.2b) không phải số nguyên, trường hợp thường gặp trong thực tế, thì giá trị tương ứng của tp có thể thấy trong Bảng G.2 bằng phép nội suy hoặc làm tròn veff xuống số nguyên nhỏ hơn tiếp theo.
CHÚ THÍCH 2: Nếu ước lượng đầu vào xi thu được từ hai hay nhiều ước lượng khác thì giá trị của vi được sử dụng với ![]() trong mẫu số của công thức (G.2b) là bậc tự do hiệu dụng tính được từ biểu thức tương đương với công thức (G.2b).
trong mẫu số của công thức (G.2b) là bậc tự do hiệu dụng tính được từ biểu thức tương đương với công thức (G.2b).
CHÚ THÍCH 3: Tùy thuộc vào nhu cầu của người sử dụng kết quả đo tiềm năng, có thể có ích, nếu bổ sung cho veff, để tính và cũng để báo cáo giá trị veffA và veffB, được tính từ phương trình G.2b xử lý riêng cho độ không đảm bảo chuẩn thu được từ đánh giá Loại A và Loại B. Nếu sự đóng góp vào ![]() của một mình độ không đảm bảo chuẩn Loại A và Loại B được ký hiệu tương ứng là
của một mình độ không đảm bảo chuẩn Loại A và Loại B được ký hiệu tương ứng là ![]() và
và ![]() thì các đại lượng khác nhau có liên hệ nhờ:
thì các đại lượng khác nhau có liên hệ nhờ:
![]() =
= ![]() +
+ ![]()
![]()
VÍ DỤ: Coi Y = f(X1, X2,X3) = bX1X2X3 và ước lượng x1, x2, x3 của các đại lượng đầu vào được phân bố chuẩn X1, X2, X3 tương ứng lá trung bình cộng của n1 = 10, n2 = 5 và n3 = 15 quan trắc lặp lại độc lập với độ không đảm bảo chuẩn tương đối u(x1)/x1 = 0,25%, u(x2)/x2 = 0,57% và u(x3)/x3 = 0,82%. Trong trường hợp này, ![]() (được đánh giá tại x1, x2, x3 – xem 5.1.2, Chú thích 1),
(được đánh giá tại x1, x2, x3 – xem 5.1.2, Chú thích 1), ![]() (xem chú thích 2 của 5.1.6), phương trình (G.2b) trở thành:
(xem chú thích 2 của 5.1.6), phương trình (G.2b) trở thành:
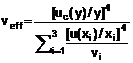
Do đó
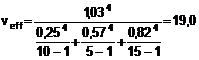
Từ Bảng G.2, giá trị của tp với p = 95% và v = 19 là t95(19) = 2,09; do đó độ không đảm bảo mở rộng tương ứng với mức tin cậy này là U95 = 2,09 x (1,03%) = 2,2%. Khi đó có thể nói rằng Y = y ± U95 = y(1 ± 0,022) (y được xác định từ y = bx1x2x3) hoặc 0,978 £ Y £ 1,022y và mức tin cậy gắn với khoảng trên gần bằng 95%.
G.4.2. Trong thực tế, uc(y) phụ thuộc vào độ không đảm bảo chuẩn u(xi) của ước lượng đầu vào cho cả đại lượng đầu vào được phân bố chuẩn và không chuẩn, u(xi) thu được từ phân bố xác suất trên cơ sở tần suất và tiên nghiệm (nghĩa là từ đánh giá Loại A và Loại B). Biểu thức tương tự áp dụng cho ước lượng y và ước lượng đầu vào xi mà y phụ thuộc. Tuy nhiên, phân bố xác suất của hàm t = (y – Y)/uc(y) có thể được tính xấp xỉ bằng phân bố t nếu được khai triển theo chuỗi Taylor quanh kỳ vọng của nó. Về cơ bản, đây là điều đạt được, theo phép tính gần đúng bậc thấp nhất, bằng công thức Welch-Satterthwaite, phương trình (G.2a) hoặc phương trình (G.2b).
Vấn đề nảy sinh là bậc tự do ấn định cho độ không đảm bảo chuẩn thu được từ đánh giá Loại B khi veff được tính từ phương trình (G.2b). Vì việc xác định thích hợp của bậc tự do thừa nhận v khi xuất hiện trong phân bố t là thước đo độ không đảm bảo của phương sai s2(![]() ), nên phương trình (E.7) trong E.4.3 có thể được sử dụng để xác định bậc tự do vi:
), nên phương trình (E.7) trong E.4.3 có thể được sử dụng để xác định bậc tự do vi:
![]() (G.3)
(G.3)
Đại lượng trong ngoặc vuông là độ không đảm bảo tương đối của u(xi); đối với đánh giá Loại B độ không đảm bảo chuẩn, đó là đại lượng chủ quan có giá trị thu được bằng đánh giá khoa học dựa trên các thông tin có sẵn.
VÍ DỤ: Coi sự hiểu biết về cách xác định ước lượng đầu vào xi và cách đánh giá độ không đảm bảo chuẩn u(xi) dẫn đến nhận định đánh giá của u(xi) tin cậy khoảng 25%. Điều này có thể có nghĩa độ không đảm bảo tương đối ![]() /
/![]() = 0,25 và do đó từ phương trình (G.3), vi = (0,25)-2/2 = 8. Nếu thay vào đó nhận định giá trị của u(xi) tin cậy chỉ khoảng 50% thì vi = 2. (Xem thêm Bảng E.1 trong Phụ lục E.)
= 0,25 và do đó từ phương trình (G.3), vi = (0,25)-2/2 = 8. Nếu thay vào đó nhận định giá trị của u(xi) tin cậy chỉ khoảng 50% thì vi = 2. (Xem thêm Bảng E.1 trong Phụ lục E.)
G.4.3. Trong thảo luận ở 4.3 và 4.4 của đánh giá độ không đảm bảo chuẩn Loại B từ một phân bố xác suất tiên nghiệm, giả định rằng giá trị của u(xi) từ đánh giá này được biết chính xác. Ví dụ, khi u(xi) thu được từ phân bố xác suất chữ nhật có nửa độ rộng được giả định a = (a+ – a–)/2 như trong 4.3.7 và 4.4.5, u(xi) = a/![]() được coi là hằng số không có độ không đảm bảo vì a+ và a–, do đó a cũng được coi như vậy (xem 4.3.9, Chú thích 2). Điều này chỉ ra thông qua phương trình (G.3) khi vi ->¥ hoặc 1/vi -> 0, nhưng nó không gây khó khăn trong việc đánh giá phương trình (G.2b). Hơn nữa, giả định vi ->¥ là rất thực tế; thực tiễn chung là chọn a+ và a– theo cách để xác suất của đại lượng đang nói tới nằm ngoài khoảng a– đến a+ là rất nhỏ.
được coi là hằng số không có độ không đảm bảo vì a+ và a–, do đó a cũng được coi như vậy (xem 4.3.9, Chú thích 2). Điều này chỉ ra thông qua phương trình (G.3) khi vi ->¥ hoặc 1/vi -> 0, nhưng nó không gây khó khăn trong việc đánh giá phương trình (G.2b). Hơn nữa, giả định vi ->¥ là rất thực tế; thực tiễn chung là chọn a+ và a– theo cách để xác suất của đại lượng đang nói tới nằm ngoài khoảng a– đến a+ là rất nhỏ.
G.5. Các xem xét khác
G.5.1. Một biểu thức được tìm thấy trong tài liệu về độ không đảm bảo đo và thường được sử dụng để nhận được độ không đảm bảo dự định cung cấp một khoảng có mức tin cậy 95% có thể được viết như sau:
![]() (G.4)
(G.4)
Ở đây ![]() được lấy từ phân bố t cho v’eff bậc tự do và p = 95%; v’eff là bậc tự do hiệu dụng tính được từ công thức Welch-Satterthwaite [phương trình (G.2b) chỉ tính đến các thành phần độ không đảm bảo chuẩn si đã được đánh giá thống kê từ các quan trắc lặp lại trong phép đo hiện hành;
được lấy từ phân bố t cho v’eff bậc tự do và p = 95%; v’eff là bậc tự do hiệu dụng tính được từ công thức Welch-Satterthwaite [phương trình (G.2b) chỉ tính đến các thành phần độ không đảm bảo chuẩn si đã được đánh giá thống kê từ các quan trắc lặp lại trong phép đo hiện hành; ![]() tính cho tất cả các thành phần khác của độ không đảm bảo, trong đó +aj và -aj là giá trị biên trên và biên dưới đã biết chính xác được giả định của Xj liên quan đến ước lượng tốt nhất xj (nghĩa là xj – aj £ Xj £ xj + aj).
tính cho tất cả các thành phần khác của độ không đảm bảo, trong đó +aj và -aj là giá trị biên trên và biên dưới đã biết chính xác được giả định của Xj liên quan đến ước lượng tốt nhất xj (nghĩa là xj – aj £ Xj £ xj + aj).
CHÚ THÍCH: Thành phần dựa trên các quan trắc lặp lại ngoài phép đo hiện hành được xử lý theo cách giống như thành phần khác được tính đến trong u2. Do đó, để thực hiện so sánh có ý nghĩa giữa phương trình (G.4) và phương trình (G.5) của điều dưới đây, giả định rằng các thành phần, nếu có, là không đáng kể.
G.5.2. Nếu độ không đảm bảo mở rộng đưa ra khoảng có mức tin cậy 95% được đánh giá theo phương pháp khuyến nghị trong G.3 và G.4, biểu thức thu được thay cho phương trình (G.4) là:
U95 = t95 (veff)(s2 + u2)1/2 (G.5)
Trong đó veff được tính từ phương trình (G.2b) và việc tính toán bao gồm tất cả thành phần độ không đảm bảo.
Trong hầu hết các trường hợp, giá trị của U95 từ phương trình (G.5) sẽ lớn hơn giá trị của U’95 từ phương trình (G.4), nếu giả định rằng trong việc đánh giá phương trình (G.5), tất cả phương trình Loại B thu được từ phân bố chữ nhật tiên nghiệm có các nửa độ rộng giống như các giá trị biên aj sử dụng để tính u2 của phương trình (G.4). Điều này có thể hiểu được bằng cách công nhận khác là cả hai thừa số đều gần 2, mặc dù trong hầu hết trường hợp t95(v’eff) sẽ lớn hơn t95 (veff); trong trường hợp (G.5) u2 được nhân với ![]() trong khi trong phương trình (G.4) nó được nhân với 3. Mặc dù hai biểu thức cho giá trị bằng nhau của U’95 và U95 với u2 << s2, U’95 sẽ nhỏ hơn U95 khoảng 13% nếu u2 << s2. Do đó, nói chung, phương trình (G.4) tạo ra độ không đảm bảo đưa ra khoảng có mức tin cậy nhỏ hơn khoảng được đưa ra bởi độ không đảm bảo mở rộng tính từ phương trình (G.5).
trong khi trong phương trình (G.4) nó được nhân với 3. Mặc dù hai biểu thức cho giá trị bằng nhau của U’95 và U95 với u2 << s2, U’95 sẽ nhỏ hơn U95 khoảng 13% nếu u2 << s2. Do đó, nói chung, phương trình (G.4) tạo ra độ không đảm bảo đưa ra khoảng có mức tin cậy nhỏ hơn khoảng được đưa ra bởi độ không đảm bảo mở rộng tính từ phương trình (G.5).
CHÚ THÍCH: Trong giới hạn u2/s2 -> ¥ và veff -> ¥, U’95 -> 1,732u trong khi U95 -> 1,960u. Trong trường hợp này U’95 đưa ra khoảng chỉ có mức tin cậy 91,7%, trong khi U95 đưa ra khoảng 95%. Trường hợp này được tính xấp xỉ trong thực tế khi thành phần thu được từ các ước lượng của biên trên và biên dưới có ưu thế hơn, nhiều về số lượng, và có giá trị của ![]() ở cỡ có thể so sánh được.
ở cỡ có thể so sánh được.
CHÚ THÍCH 2: Đối với phân bố chuẩn, hệ số phủ k = ![]() đưa ra một khoảng với mức tin cậy p = 91,673…%. Giá trị này của p là ổn định theo nghĩa độ lệch nhỏ của đại lượng đầu vào độc lập nhất so với tính chuẩn, khi so sánh với giá trị khác.
đưa ra một khoảng với mức tin cậy p = 91,673…%. Giá trị này của p là ổn định theo nghĩa độ lệch nhỏ của đại lượng đầu vào độc lập nhất so với tính chuẩn, khi so sánh với giá trị khác.
G.5.3. Đôi khi đại lượng đầu vào Xi được phân bố bất đối xứng – độ lệch khỏi giá trị kỳ vọng của một dấu có nhiều khả năng hơn độ lệch của dấu ngược lại (xem 4.3.8). Mặc dù điều này không tạo ra sự khác nhau trong sự đánh giá độ không đảm bảo chuẩn u(xi) của ước lượng xi của Xi và do đó trong đánh giá uc(y), nhưng có thể ảnh hưởng đến tính toán U.
Thường sẽ là thuận tiện khi cho khoảng đối xứng, Y = y ± U, trừ khi khoảng đó đúng như vậy thì sẽ có khác nhau lớn giữa độ lệch của một phía so với phía kia. Nếu sự bất đối xứng của Xi chỉ gây ra bất đối xứng nhỏ trong phân bố xác suất đặc trưng bằng kết quả đo y và độ không đảm bảo chuẩn tổng hợp uc(y), thì xác suất mất trên một phía do đưa ra khoảng đối xứng được bù bằng xác suất thu được ở phía kia. Sự lựa chọn là để đưa ra khoảng đối xứng về xác suất (và do đó bất đối xứng trong U): xác suất mà Y nằm dưới giới hạn dưới y – U–bằng xác suất mà Y nằm trên giới hạn trên y + U+. Nhưng để trích dẫn các giới hạn này, cần nhiều thông tin hơn các ước lượng đơn giản y và uc(y) [và do đó nhiều thông tin hơn các ước lượng đơn giản xi và u(xi) của từng đại lượng đầu vào Xi].
G.5.4. Việc đánh giá độ không đảm bảo mở rộng Up cho ở đây theo uc(y), veff và thừa số tp(veff) từ phân bố t chỉ là phép tính gần đúng và nó có mặt hạn chế. Phân bố của (y-Y)/uc(y) được cho bởi phân bố t chỉ khi phân bố của Y là chuẩn, ước lượng y và độ không đảm bảo chuẩn tổng hợp uc(y) là độc lập và nếu phân bố của ![]() là phân bố c2. Việc đưa vào veff, phương trình (G.2b), chỉ giải quyết vấn đề nói đến sau, và cung cấp phân bố c2 gần đúng cho
là phân bố c2. Việc đưa vào veff, phương trình (G.2b), chỉ giải quyết vấn đề nói đến sau, và cung cấp phân bố c2 gần đúng cho ![]() ; mặt khác của vấn đề, phát sinh từ tính không chuẩn của phân bố của Y, yêu cầu việc xem xét các mô men bậc cao hơn bổ sung cho phương sai.
; mặt khác của vấn đề, phát sinh từ tính không chuẩn của phân bố của Y, yêu cầu việc xem xét các mô men bậc cao hơn bổ sung cho phương sai.
G.6. Tổng kết và kết luận
G.6.1. Hệ số phủ kp đưa ra khoảng có mức tin cậy p gần mức quy định có thể chỉ tìm thấy nếu có sự hiểu biết rộng về phân bố xác suất của từng đại lượng đầu vào và nếu các phân bố đó được tổng hợp để thu được phân bố của đại lượng đầu ra. Bản thân ước lượng đầu vào xi và độ không đảm bảo chuẩn của chúng u(xi) là không thích hợp cho mục đích này.
G.6.2. Vì tính toán mở rộng được yêu cầu với phân bố xác suất tổng hợp hiếm khi được chứng minh bằng phạm vi và độ tin cậy của thông tin có sẵn, phép tính gần đúng cho phân bố của đại lượng đầu ra là có thể chấp nhận được. Vì lý thuyết giới hạn trung tâm thường đủ để giả định rằng phân bố xác suất của (y – Y)/uc(y) là phân bố t và lấy kp = tp(veff), với hệ số t dựa trên bậc tự do hiệu dụng veff của uc(y) thu được từ công thức Welch-Satterthwaite, phương trình (G.2b).
G.6.3. Để thu được veff từ phương trình (G.2b) cần có bậc tự do vi đối với từng thành phần độ không đảm bảo chuẩn. Đối với thành phần thu được từ đánh giá Loại A, vi thu được từ số quan trắc lặp lại độc lập mà ước lượng đầu vào dựa trên đó và số đại lượng độc lập được xác định từ các quan trắc đó (xem G.3.3). Đối với thành phần thu được từ đánh giá Loại B, vi thu được từ độ tin cậy được đánh giá của giá trị của thành phần đó [xem G.4.2 và phương trình (G.3)]
G.6.4. Sau đây tóm tắt phương pháp tính độ không đảm bảo mở rộng thường dùng Up = kpuc(y) dự định cung cấp khoảng Y = y ± Up có mức tin cậy gần đúng p:
1) Thu được y và uc(y) như mô tả trong Điều 4 và 5.
2) Tính veff từ công thức Welch-Satterthwaite, phương trình (G.2b) (được nhắc lại ở đây để tiện tham khảo)
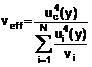 (G.2b)
(G.2b)
Nếu u(xi) thu được từ đánh giá Loại A thì xác định vi như được chỉ ra trong G.3.3. Nếu u(xi) thu được từ đánh giá Loại B và nó có thể được coi như đã biết chính xác, thường là tình huống trong thực tế, vi -> ¥; mặt khác, ước lượng vi từ phương trình (G.3).
3) Thu được t hệ số tp(veff) với mức tin cậy mong muốn p từ Bảng G.2. Nếu veff không phải là số nguyên thì nội suy hoặc làm tròn veff xuống số nguyên nhỏ hơn tiếp theo.
4) Lấy kp = tp(veff) và tính Up = kpuc(y).
G.6.5. Trong một số trường hợp, không xảy ra quá thường xuyên trong thực tế, điều kiện được yêu cầu bởi lý thuyết giới hạn trung tâm có thể không được thỏa mãn hoàn toàn và cách tiếp cận G.6.4 có thể dẫn tới kết quả không chấp nhận được. Ví dụ, nếu uc(y) bị chi phối bởi thành phần của độ không đảm bảo được đánh giá từ phân bố chữ nhật có các giá trị biên được giả định là biết chính xác thì có thể [nếu tp(veff) >![]() ] là y – Up và y + Up, giới hạn trên và dưới của khoảng được xác định bởi Up, có thể nằm ngoài giá trị biên của phân bố xác suất của đại lượng đầu ra Y. Trường hợp như vậy phải được giải quyết trên cơ sở riêng nhưng thường tuân theo xử lý phân tích gần đúng (ví dụ: bao gồm việc tích chập phân bố chuẩn của phân bố chữ nhật [10]).
] là y – Up và y + Up, giới hạn trên và dưới của khoảng được xác định bởi Up, có thể nằm ngoài giá trị biên của phân bố xác suất của đại lượng đầu ra Y. Trường hợp như vậy phải được giải quyết trên cơ sở riêng nhưng thường tuân theo xử lý phân tích gần đúng (ví dụ: bao gồm việc tích chập phân bố chuẩn của phân bố chữ nhật [10]).
G.6.6. Đối với nhiều phép đo thực tế trong nhiều lĩnh vực, các điều kiện sau chiếm ưu thế:
– ước lượng y của đại lượng đo Y thu được từ ước lượng xi của một số lượng đáng kể các đại lượng đầu vào Xi có thể được mô tả bằng phân bố xác suất thể hiện tốt nhất, như phân bố chuẩn và chữ nhật;
– độ không đảm bảo chuẩn u(xi) của các ước lượng này, có thể thu được từ đánh giá Loại A hoặc Loại B, đóng góp lượng so sánh được vào độ không đảm bảo chuẩn tổng hợp uc(y) của kết quả đo y;
– phép tính gần đúng tuyến tính được thể hiện bằng định luật lan truyền độ không đảm bảo là thích hợp (xem 5.1.2 và E.3.1);
– độ không đảm bảo của uc(y) nhỏ hợp lý vì bậc tự do hiệu dụng veff có độ lớn đáng kể, tức là lớn hơn 10.
Trong các trường hợp này, phân bố xác suất được đặc trưng bởi kết quả đo và độ không đảm bảo chuẩn tổng hợp có thể được giả định là chuẩn theo lý thuyết giới hạn trung tâm; uc(y) có thể được lấy làm ước lượng khá tin cậy của độ lệch chuẩn của phân bố chuẩn đó vì độ lớn đáng kể của veff. Khi đó, dựa trên thảo luận được nêu trong phụ lục này, bao gồm sự nhấn mạnh bản chất gần đúng của quá trình đánh giá độ không đảm bảo và tính không thực tế của việc cố gắng phân biệt khoảng có mức tin cậy khác nhau một hoặc hai phần trăm, có thể thực hiện như sau:
– cho k = 2 và giả định rằng U = 2uc(y) xác định một khoảng có mức tin cậy xấp xỉ 95%;
Hoặc, đối với nhiều ứng dụng quan trọng hơn,
– cho k = 3 và giả định rằng U = 3uc(y) xác định một khoảng có mức tin cậy xấp xỉ 99%;
Mặc dù cách tiếp cận này cần phù hợp với nhiều phép đo thực tế, khả năng ứng dụng của nó với mỗi phép đo cụ thể sẽ phụ thuộc vào k = 2 phải gần như thế nào với t95(veff) hoặc k = 3 phải gần như thế nào với t99(veff); nghĩa là mức tin cậy của khoảng được xác định bằng U = 2uc(y) hoặc U = 3uc(y) lần lượt phải gần như thế nào với 95% hoặc 99%. Mặc dù đối với veff = 11, k = 2 và k = 3 đánh giá thấp t95(11) và t99(11) lần lượt chỉ khoảng 10% và 4% (xem Bảng G.2) nhưng điều này không thể chấp nhận được trong một số trường hợp. Hơn nữa, với tất cả các giá trị của veff lớn hơn 13, k = 3 tạo ra một khoảng có mức tin cậy lớn hơn 99%. (Xem Bảng G.2, cũng chỉ ra rằng đối với veff ->¥ mức tin cậy của khoảng được tạo ra bởi k = 2 và k = 3 lần lượt là 95,45% và 99,73%). Do đó, trong thực tế, độ lớn của veff và yêu cầu đặt ra đối với độ không đảm bảo mở rộng sẽ xác định cách tiếp cận này có thể được sử dụng hay không.
Bảng G.2 – Giá trị của tp(v) từ phân bố t đối với bậc tự do v xác định khoảng -tp(v) đến +tp(v) chứa phần p của phân bố
|
Bậc tự do |
phần p theo phần trăm |
|||||
|
68,27a) |
90 |
95 |
95,45a) |
99 |
99,73a) |
|
|
1 |
1,84 |
6,31 |
12,71 |
13,97 |
63,66 |
235,80 |
|
2 |
1,32 |
2,92 |
4,30 |
4,53 |
9,92 |
19,21 |
|
3 |
1,20 |
2,35 |
3,18 |
3,31 |
5,84 |
9,22 |
|
4 |
1,14 |
2,13 |
2,78 |
2,87 |
4,60 |
6,62 |
|
5 |
1,11 |
2,02 |
2,57 |
2,65 |
4,03 |
5,51 |
|
|
|
|
|
|
|
|
|
6 |
1,09 |
1,94 |
2,45 |
2,52 |
3,71 |
4,90 |
|
7 |
1,08 |
1,89 |
2,36 |
2,43 |
3,50 |
4,53 |
|
8 |
1,07 |
1,86 |
2,31 |
2,37 |
3,36 |
4,28 |
|
9 |
1,06 |
1,83 |
2,26 |
2,32 |
3,25 |
4,09 |
|
10 |
1,05 |
1,81 |
2,23 |
2,28 |
3,17 |
3,96 |
|
|
|
|
|
|
|
|
|
11 |
1,05 |
1,80 |
2,20 |
2,25 |
3,11 |
3,85 |
|
12 |
1,04 |
1,78 |
2,18 |
2,23 |
3,05 |
3,76 |
|
13 |
1,04 |
1,77 |
2,16 |
2,21 |
3,01 |
3,69 |
|
14 |
1,04 |
1,76 |
2,14 |
2,20 |
2,98 |
3,64 |
|
15 |
1,03 |
1,75 |
2,13 |
2,18 |
2,95 |
3,59 |
|
|
|
|
|
|
|
|
|
16 |
1,03 |
1,75 |
2,12 |
2,17 |
2,92 |
3,54 |
|
17 |
1,03 |
1,74 |
2,11 |
2,16 |
2,90 |
3,51 |
|
18 |
1,03 |
1,73 |
2,10 |
2,15 |
2,88 |
3,48 |
|
19 |
1,03 |
1,73 |
2,09 |
2,14 |
2,86 |
3,45 |
|
20 |
1,03 |
1,72 |
2,09 |
2,13 |
2,85 |
3,42 |
|
|
|
|
|
|
|
|
|
25 |
1,02 |
1,71 |
2,06 |
2,11 |
2,79 |
3,33 |
|
30 |
1,02 |
1,70 |
2,04 |
2,09 |
2,75 |
3,27 |
|
35 |
1,01 |
1,70 |
2,03 |
2,07 |
2,72 |
3,23 |
|
40 |
1,01 |
1,68 |
2,02 |
2,06 |
2,70 |
3,20 |
|
45 |
1,01 |
1,68 |
2,01 |
2,06 |
2,69 |
3,18 |
|
|
|
|
|
|
|
|
|
50 |
1,01 |
1,68 |
2,01 |
2,05 |
2,68 |
3,16 |
|
100 |
1,005 |
1,660 |
1,984 |
2,025 |
2,626 |
3,077 |
|
¥ |
1,000 |
1,645 |
1,960 |
2,000 |
2,576 |
3,000 |
|
a) Đối với đại lượng z được mô tả bằng phân bố chuẩn với kỳ vọng mz và độ lệch chuẩn s, khoảng mz ± ks bao gồm p = 68,27%, 95,45% và 99,73% của phân bố tương ứng với k = 1, 2 và 3. |
||||||
PHỤ LỤC H
(tham khảo)
VÍ DỤ
Phụ lục này đưa ra sáu ví dụ, H.1 đến H.6, được đề cập khá chi tiết nhằm minh họa cho các nguyên tắc cơ bản được giới thiệu trong tiêu chuẩn này về đánh giá và trình bày độ không đảm bảo đo. Cùng với các ví dụ trong phần nội dung chính và trong một số phần của các phụ lục khác, các ví dụ này cho phép người sử dụng tiêu chuẩn áp dụng các nguyên tắc vào thực tiễn công việc.
Vì các ví dụ có mục đích minh họa nên chúng cần được đơn giản hóa. Hơn nữa, ví chúng và dữ liệu bằng số sử dụng trong đó được chọn chủ yếu để giải thích các nguyên tắc của tiêu chuẩn này nên chúng cũng như các dữ liệu không nhất thiết được hiểu là mô tả các phép đo thực sự. Trong khi dữ liệu được sử dụng như được đưa ra, để tránh sai số do làm tròn, các chữ số được giữ lại trong các phép tính trung gian nhiều hơn bình thường. Do đó kết quả tính toán công bố của phép tính có nhiều đại lượng có thể hơi khác với kết quả được biểu thị bằng trị số đã nêu trong tài liệu về các đại lượng này.
Các phần trước của tiêu chuẩn này đã chỉ rõ việc phân loại các phương pháp sử dụng để đánh giá thành phần của độ không đảm bảo như Loại A hoặc Loại B chỉ để thuận tiện; điều đó cần thiết đối với việc xác định độ không đảm bảo chuẩn tổng hợp hoặc độ không đảm bảo mở rộng của kết quả đo vì tất cả các thành phần của độ không đảm bảo, dù chúng được đánh giá như thế nào, đều được xử lý theo cùng một cách (xem 3.3.4, 5.1.2 và E.3.7). Do đó, trong các ví dụ, phương pháp được sử dụng để đánh giá thành phần cụ thể của độ không đảm bảo không được xác định cụ thể theo loại của nó. Tuy nhiên, sẽ dễ hiểu hơn nếu thảo luận về thành phần được từ đánh giá Loại A hay Loại B.
H.1. Hiệu chuẩn can mẫu
Ví dụ này chứng minh rằng thậm chí một phép đo bề ngoài đơn giản có thể bao gồm các khía cạnh chi tiết của đánh giá độ không đảm bảo.
H.1.1. Vấn đề của phép đo
Độ dài của can mẫu danh nghĩa 50 mm được xác định bằng cách so sánh với chuẩn đã biết có cùng độ dài danh nghĩa. Đầu ra trực tiếp của phép so sánh hai can mẫu này là chênh lệch d về chiều dài của chúng:
![]() (H.1)
(H.1)
Trong đó
ℓ đại lượng đo, nghĩa là, độ dài ở 200C của can mẫu được hiệu chuẩn;
ℓs độ dài của chuẩn ở 200C theo giấy chứng nhận hiệu chuẩn;
a và as là hệ số giãn nở nhiệt độ tương ứng của dụng cụ được hiệu chuẩn và chuẩn;
θ và θs là độ lệch nhiệt độ so với nhiệt độ quy chiếu 200C tương ứng của can mẫu và chuẩn.
H.1.2. Mô hình toán
Từ phương trình (H.1), đại lượng đo được cho bởi
![]() (H.2)
(H.2)
Nếu chênh lệch nhiệt độ giữa can mẫu được hiệu chuẩn và chuẩn là dθ = θ – θs và chênh lệch hệ số giãn nở nhiệt của chúng là da = a – as thì phương trình (H.2) trở thành
![]() (H.3)
(H.3)
Chênh lệch dθ và da, nhưng không phải độ không đảm bảo của chúng, được ước lượng bằng “không”; da, as, dθ và θ được giả định là không tương quan. (Nếu đại lượng đo được thể hiện theo các biến θ, θs, a và as thì cần phải tính đến sự tương quan giữa θ và θs, giữa a và as.)
Do đó theo phương trình (H.3), ước lượng giá trị của đại lượng đo ℓ có thể thu được từ biểu thức đơn giản ![]() , trong đó
, trong đó![]() là độ dài của chuẩn ở 200C như được nêu trong giấy chứng nhận hiệu chuẩn và d được ước lượng bằng
là độ dài của chuẩn ở 200C như được nêu trong giấy chứng nhận hiệu chuẩn và d được ước lượng bằng![]() , trung bình cộng của n = 5 quan trắc lặp lại độc lập. Độ không đảm bảo chuẩn tổng hợp uc(ℓ) của ℓ thu được bằng cách áp dụng phương trình (10) trong 5.1.2 vào (H.3), như được mô tả dưới đây.
, trung bình cộng của n = 5 quan trắc lặp lại độc lập. Độ không đảm bảo chuẩn tổng hợp uc(ℓ) của ℓ thu được bằng cách áp dụng phương trình (10) trong 5.1.2 vào (H.3), như được mô tả dưới đây.
CHÚ THÍCH: Trong ví dụ này và các ví dụ khác, để đơn giản hóa, cùng một ký hiệu được sử dụng cho đại lượng và ước lượng của nó.
H.1.3. Các phương sai đóng góp vào độ không đảm bảo
Các khía cạnh thích hợp của ví dụ này được thảo luận ở đây và các điều tiếp theo được tổng kết trong Bảng H.1.
Vì giả định rằng da = 0 và dθ = 0 nên việc áp dụng phương trình (10) trong 5.1.2 vào phương trình H.3 tạo ra
![]() (H.4)
(H.4)
Với
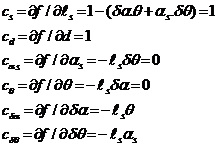
Và do đó
![]() (H.5)
(H.5)
H.1.3.1. Độ không đảm bảo của phép hiệu chuẩn chuẩn, u(ℓs)
Giấy chứng nhận hiệu chuẩn đưa ra độ không đảm bảo mở rộng của chuẩn U = 0,075 mm và nêu rõ nó thu được bằng cách sử dụng hệ số phủ k = 3. Độ không đảm bảo chuẩn khi đó là
u(ℓs) = (0,075 mm)/ 3 = 25 nm
H.1.3.2. Độ không đảm bảo của chênh lệch độ dài đo được, u(d)
Độ lệch chuẩn thực nghiệm tích lũy đặc trưng cho sự so sánh ℓ và ℓs được xác định từ độ biến động của 25 quan trắc lặp lại độc lập về chênh lệch độ dài của hai can mẫu tìm được bằng 13 nm. Trong phép so sánh của ví dụ này, tiến hành năm quan trắc lặp lại. Độ không đảm bảo chuẩn gắn với trung bình cộng của các số đọc khi đó bằng (xem 4.2.4):
![]()
Theo giấy chứng nhận hiệu chuẩn của thiết bị so sánh được sử dụng để so sánh ℓ với ℓs, độ không đảm bảo của nó “do sai số ngẫu nhiên” là ±0,01 mm ở mức tin cậy 95% và được dựa trên 6 phép đo lặp; do đó, sử dụng thừa số t t95(5) = 2,57 đối với bậc tự do v = 6 – 1 = 5 (xem Phụ lục G, Bảng G.2), độ không đảm bảo chuẩn là:
u(d1) = (0,01 mm)/2,57 = 3,9 nm
Độ không đảm bảo của thiết bị so sánh “do sai số hệ thống” được nêu trong giấy chứng nhận là 0,02 mm ở “mức ba sigma”. Vì vậy, độ không đảm bảo chuẩn do nguyên nhân này có thể được lấy bằng:
u(d2) = (0,02 mm)/3 = 6,7 nm
Đóng góp tổng hợp thu được từ tổng các phương sai ước lượng
![]()
Hoặc
u(d) = 9,7 nm
H.1.3.3. Độ không đảm bảo của hệ số giãn nở nhiệt, u(as)
Hệ số giãn nở nhiệt của thiết bị so sánh được cho là as = 11,5 x 10-6 0C-1 với độ không đảm bảo được biểu thị bằng phân bố chữ nhật với các giá trị biên ±2 x 10-6 0C-1. Khi đó, độ không đảm bảo chuẩn bằng [xem phương trình (7) trong 4.3.7]
U(as) = (2 x 10-6 0C-1)/![]() = 1,2 x 10-6 0C-1.
= 1,2 x 10-6 0C-1.
Vì ![]() như trình bày trong H.1.3, độ không đảm bảo này không góp phần vào độ không đảm bảo của ℓ ở bậc một. Tuy nhiên nó có đóng góp ở bậc hai được thảo luận ở H.1.7.
như trình bày trong H.1.3, độ không đảm bảo này không góp phần vào độ không đảm bảo của ℓ ở bậc một. Tuy nhiên nó có đóng góp ở bậc hai được thảo luận ở H.1.7.
Bảng H.1 – Tóm tắt các thành phần của độ không đảm bảo chuẩn
|
Thành phần độ không đảm bảo chuẩn |
Nguồn của độ không đảm bảo |
Giá trị của độ không đảm bảo chuẩn |
|
ui(ℓ) ≡ |ci|u(xi) |
Bậc tự do |
|
u(ℓs) |
Hiệu chuẩn can mẫu chuẩn |
25 nm |
1 |
25 |
18 |
|
u(d) u(d1) u(d2) |
Chênh lệch đo được giữa các can mẫu
quan trắc lặp lại ảnh hưởng ngẫu nhiên của thiết bị so sánh ảnh hưởng hệ thống của thiết bị so sánh |
9,7 nm
5,8 nm 3,9 nm
6,7 nm |
1 |
9,7 |
25,6
24 5
8 |
|
u(as) |
Hệ số giãn nở nhiệt của can mẫu chuẩn |
1,2 x 10-6 0C-1 |
0 |
0 |
|
|
u(θ) u(Δ) |
Nhiệt độ của bệ thử nhiệt độ trung bình của bệ biến động theo chu kỳ của nhiệt độ phòng |
0,410C 0,20C
0,350C |
0 |
0 |
|
|
u(da) |
Chênh lệch hệ số giãn nở của các can mẫu |
0,58 x 10-6 0C-1 |
-ℓsθ |
2,9 |
50 |
|
u(dθ) |
Chênh lệch nhiệt độ của các can mẫu |
0,0290C |
-ℓsas |
16,6 |
2 |
|
uc(ℓ) = 32 nm veff(ℓ) = 16 |
|||||
H.1.3.4. Độ không đảm bảo của độ lệch nhiệt độ can mẫu, u(θ)
Nhiệt độ của bệ thử được báo cáo là (19,9±0,5)0C; nhiệt độ tại thời điểm quan trắc riêng lẻ không được ghi lại. Độ bù tối đa được nêu, Δ = 0,50C, là đặc trưng cho độ lớn của biến động theo chu kỳ của nhiệt độ trong hệ nhiệt tĩnh, không phải độ không đảm bảo của nhiệt độ trung bình. Giá trị của độ lệch nhiệt độ trung bình là:
![]() = 19,90C – 200C = -0,10C
= 19,90C – 200C = -0,10C
Được báo cáo là bản thân nó có độ không đảm bảo chuẩn do độ không đảm bảo của nhiệt độ trung bình của bệ thử là:
U(![]() ) = 0,20C.
) = 0,20C.
Trong khi biến động chu kỳ theo thời gian tạo ra phân bố (arcsin) hình chữ U của nhiệt độ dẫn đến độ không đảm bảo chuẩn:
![]()
Độ lệch nhiệt độ θ có thể được lấy bằng ![]() và độ không đảm bảo chuẩn của θ thu được từ:
và độ không đảm bảo chuẩn của θ thu được từ:
![]()
Suy ra
u(θ) = 0,410C
Vì ![]() như đã trình bày trong H.1.3, độ không đảm bảo này cũng không góp phần vào độ không đảm bảo của l bậc nhất nhưng nó có đóng góp ở bậc hai được thảo luận ở H.1.7.
như đã trình bày trong H.1.3, độ không đảm bảo này cũng không góp phần vào độ không đảm bảo của l bậc nhất nhưng nó có đóng góp ở bậc hai được thảo luận ở H.1.7.
H.1.3.5. Độ không đảm bảo của chênh lệch hệ số giãn nở, u(da)
Giá trị biên ước lượng về biến đổi của da là ±1 x 10-6 0C-1 với xác suất bằng nhau của da có mọi giá trị bất kỳ trong phạm vi biên đó. Độ không đảm bảo chuẩn bằng
u(da) = (1 x 10-6 0C-1)/![]() = 0,58 x 10-6 0C-1
= 0,58 x 10-6 0C-1
H.1.3.6. Độ không đảm bảo của chênh lệch nhiệt độ của các can mẫu, u(dθ)
Chuẩn và can mẫu kiểm tra được kỳ vọng là ở cùng một nhiệt độ nhưng chênh lệch nhiệt độ có thể tồn tại với xác suất như nhau ở bất kỳ đâu trong khoảng đã ước lượng từ -0,050C đến +0,050C. Độ không đảm bảo chuẩn rằng:
u(dθ) = 0,050C/![]() = 0,0290C
= 0,0290C
H.1.4. Độ không đảm bảo chuẩn tổng hợp
Độ không đảm bảo chuẩn tổng hợp uc(ℓ) được tính từ phương trình (H.5). Các số hạng riêng lẻ được tập hợp và thay vào biểu thức này để thu được
![]() = (25nm)2 + (9,7 nm)2 + (0,05 m)2(0,10C)2(0,58×10-6 0C-1)2 (H.6a)
= (25nm)2 + (9,7 nm)2 + (0,05 m)2(0,10C)2(0,58×10-6 0C-1)2 (H.6a)
+ (0,05 m)2(11,5 x 10-6 0C-1)2 (0,029 0C)2
= (25 nm)2 + (9,7 nm)2 + (2,9 nm)2 + (16,6 nm)2 = 1 002 nm2 (H.6b)
Hoặc
![]() = 32 nm (H.6c)
= 32 nm (H.6c)
Thành phần chính của độ không đảm bảo rõ ràng là của chuẩn, u(ℓs) = 25 nm.
H.1.5. Kết quả cuối cùng
Giấy chứng nhận hiệu chuẩn đối với can mẫu chuẩn cho ℓs = 50,000 623 mm là độ dài ở 200C. Trung bình cộng ![]() của năm quan trắc lặp lại của chênh lệch độ dài giữa can mẫu chưa biết và can mẫu chuẩn là 215 nm. Do đó, vì ℓ = ℓs +
của năm quan trắc lặp lại của chênh lệch độ dài giữa can mẫu chưa biết và can mẫu chuẩn là 215 nm. Do đó, vì ℓ = ℓs + ![]() (xem H.1.2) nên độ dài ℓ của can mẫu chưa biết ở 200C là 50,000 838 mm. Theo 7.2.2, kết quả cuối cùng của phép đo có thể được nêu là:
(xem H.1.2) nên độ dài ℓ của can mẫu chưa biết ở 200C là 50,000 838 mm. Theo 7.2.2, kết quả cuối cùng của phép đo có thể được nêu là:
ℓs = 50,000 838 mm với độ không đảm bảo chuẩn tổng hợp uc = 32 nm. Độ không đảm bảo chuẩn tổng hợp tương đối tương ứng là uc/ℓ = 6,4 x 10-7.
H.1.6. Độ không đảm bảo mở rộng
Giả sử rằng, cần nhận được độ không đảm bảo mở rộng U99 = k99uc(ℓ) để đưa ra khoảng có mức tin cậy xấp xỉ 99%. Thủ tục sử dụng được tóm tắt trong G.6.4 và bậc tự do yêu cầu được trình bày trong Bảng H.1. Những bậc tự do này thu được như sau:
1) Độ không đảm bảo của phép hiệu chuẩn chuẩn, u(ℓs) [H.1.3.1]. Giấy chứng nhận hiệu chuẩn nêu rõ rằng bậc tự do hiệu dụng của độ không đảm bảo chuẩn tổng hợp từ đó thu được độ không đảm bảo mở rộng được trích dẫn là veff(ℓs) = 18.
2) Độ không đảm bảo của chênh lệch chiều dài đo được, u(d) [H.1.3.2]. Mặc dù ![]() thu được từ năm quan trắc lặp lại, vì u(
thu được từ năm quan trắc lặp lại, vì u(![]() ) thu được từ độ lệch chuẩn thực nghiệm tích lũy dựa trên 25 quan trắc nên bậc tự do của u(
) thu được từ độ lệch chuẩn thực nghiệm tích lũy dựa trên 25 quan trắc nên bậc tự do của u(![]() ) bằng v(
) bằng v(![]() ) = 25 – 1 = 24 (xem H.3.6, chú thích). Bậc tự do của u(d1), độ không đảm bảo do ảnh hưởng ngẫu nhiên của thiết bị so sánh, bằng v(d1) = 6 -1 = 5 vì d1 thu được từ sáu phép đo lặp lại. Độ không đảm bảo ±0,02 mm đối với ảnh hưởng hệ thống lên thiết bị so sánh có thể được giả định là tin cậy đến 25% và do đó bậc tự do từ phương trình (G.3) trong G.4.2 là v(d2) = 8 (xem ví dụ của G.4.2). Khi đó, bậc tự do hiệu dụng của u(d), veff(d) thu được từ phương trình (G.2b) trong G.4.1:
) = 25 – 1 = 24 (xem H.3.6, chú thích). Bậc tự do của u(d1), độ không đảm bảo do ảnh hưởng ngẫu nhiên của thiết bị so sánh, bằng v(d1) = 6 -1 = 5 vì d1 thu được từ sáu phép đo lặp lại. Độ không đảm bảo ±0,02 mm đối với ảnh hưởng hệ thống lên thiết bị so sánh có thể được giả định là tin cậy đến 25% và do đó bậc tự do từ phương trình (G.3) trong G.4.2 là v(d2) = 8 (xem ví dụ của G.4.2). Khi đó, bậc tự do hiệu dụng của u(d), veff(d) thu được từ phương trình (G.2b) trong G.4.1:
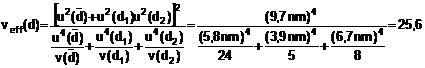
3) Độ không đảm bảo của chênh lệch hệ số giãn nở, u(da), [H.1.3.5]. Các biên ước lượng ±1 x 10-6 0C-1 trên độ biến động của da được cho là tin cậy đến 10%. Điều này, từ phương trình (G.3) trong G.4.2 suy ra v(da) = 50.
4) Độ không đảm bảo của chênh lệch nhiệt độ của các can mẫu, u(dθ), [H.1.3.6]. Khoảng được ước lượng từ – 0,050C đến + 0,050C đối với chênh lệch nhiệt độ dθ được tin là chỉ tin cậy đến 50%, từ phương trình (G.3) trong G.4.2 cho v(dθ) =2.
Việc tính toán veff(ℓ) từ phương trình (G.2b) trong G.4.1 cũng tiến hành đúng như tính toán veff(d) trong điểm 2) ở trên. Do đó từ phương trình (H.6b), (H.6c) và các giá trị của v được cho trong các điểm từ 1) đến 4).
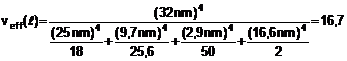
Để nhận được độ không đảm bảo mở rộng yêu cầu, giá trị này đầu tiên được làm tròn xuống số nguyên nhỏ hơn gần nhất, veff(ℓ) = 16. Khi đó, theo Bảng G.2 trong Phụ lục G t99(16) = 2,92 và do đó U99 = t99(16)uc(ℓ) = 2,92 x (32 nm) = 93 nm. Theo 7.2.4, kết quả cuối cùng của phép đo có thể được đưa ra là:
ℓ = (50,000 838 ± 0,000 093) mm, trong đó số đứng sau dấu ± là trị số của độ không đảm bảo mở rộng U = kuc, với U được xác định từ độ không đảm bảo chuẩn tổng hợp uc = 32 nm và hệ số phủ k = 2,92 được dựa trên phân bố t đối với bậc tự do v = 16 và xác định khoảng được ước lượng để có mức tin cậy 99%. Độ không đảm bảo mở rộng tương đối tương ứng là U/ℓ = 1,9 x 10-6.
H.1.7. Số hạng bậc hai
Chú thích của 5.1.2 chỉ ra rằng phương trình (10), được sử dụng trong ví dụ này để thu được độ không đảm bảo chuẩn tổng hợp uc(ℓ), phải được làm tăng lên khi tính phi tuyến của hàm Y = f(X1, X2, … XN) là rất đáng kể, như vậy không thể bỏ qua các số hạng bậc cao hơn trong khai triển chuỗi Taylor. Đây là trường hợp trong ví dụ này và do đó việc đánh giá uc(ℓ) như đã trình bày ở mục này là không đầy đủ. Việc áp dụng biểu thức được nêu trong chú thích của 5.1.2 vào phương trình (H.3) thực tế mang lại hai số hạng bậc hai riêng biệt không thể bỏ qua được cộng vào phương trình (H.5). Các số hạng này, xuất hiện từ số hạng bậc hai trong biểu thức ở chú thích là:
![]()
Nhưng chỉ các số hạng bậc một có đóng góp đáng kể vào uc(ℓ)
![]() (0,05 m)(0,58 x 10-6 0C-1)(0,410C) = 11,7 nm
(0,05 m)(0,58 x 10-6 0C-1)(0,410C) = 11,7 nm
![]() (0,05 m)(1,2 x 10-6 0C-1)(0,0290C) = 1,7 nm
(0,05 m)(1,2 x 10-6 0C-1)(0,0290C) = 1,7 nm
Các số hạng bậc hai làm uc(ℓ) tăng từ 32 nm lên 34 nm.
H.2. Phép đo điện trở và điện kháng đồng thời
Ví dụ này minh họa cách xử lý nhiều đại lượng đo hoặc đại lượng đầu vào được xác định đồng thời trong cùng một phép đo và sự tương quan giữa các ước lượng của chúng. Chỉ xem xét biến động ngẫu nhiên của các quan trắc; trong thực hành, độ không đảm bảo của sự hiệu chính cho ảnh hưởng hệ thống cũng góp phần vào độ không đảm bảo của kết quả đo. Dữ liệu được phân tích theo hai cách khác nhau, với từng cách về cơ bản thu được các trị số giống nhau.
H.2.1. Vấn đề của phép đo
Điện trở R và điện kháng X của phần tử mạch điện được xác định bằng cách đo biên độ V của hiệu điện thế xoay chiều hình sin đi qua các cực của nó, biên độ I của dòng xoay chiều đi qua và góc dịch pha Ø của hiệu điện thế xoay chiều liên quan đến dòng xoay chiều. Do đó ba đại lượng đầu vào là V, I và Ø và ba đại lượng đầu ra – đại lượng đo – là ba thành phần trở kháng R, X và Z. Vì Z2 = R2 + X2 nên chỉ có hai đại lượng đầu ra độc lập.
H.2.2. Mô hình toán và dữ liệu
Các đại lượng đo liên hệ với đại lượng đầu vào theo định luật Ôm:
![]() ;
; ![]() ;
; ![]() (H.7)
(H.7)
Xét năm tập hợp độc lập các quan trắc đồng thời của ba đại lượng đầu vào V, I và Ø thu được ở điều kiện giống nhau (xem B.2.15), dẫn đến dữ liệu được nêu trong Bảng H.2. Trung bình cộng của các quan trắc và độ lệch chuẩn thực nghiệm của các trung bình đó được tính từ phương trình (3) và (5) trong 4.2 cũng được đưa ra. Các trung bình được lấy làm ước lượng tốt nhất của giá trị mong muốn của các đại lượng đầu vào và độ lệch chuẩn thực nghiệm là độ không đảm bảo chuẩn của các trung bình đó.
Vì các trung bình, ![]() ,
, ![]() và
và ![]() thu được từ các quan trắc đồng thời nên chúng có tương quan và sự tương quan phải được tính đến trong việc đánh giá độ không đảm bảo chuẩn của các đại lượng đo R, X và Z. Hệ số tương quan được yêu cầu dễ dàng thu được từ phương trình (14) trong 5.2.2 sử dụng giá trị của s(
thu được từ các quan trắc đồng thời nên chúng có tương quan và sự tương quan phải được tính đến trong việc đánh giá độ không đảm bảo chuẩn của các đại lượng đo R, X và Z. Hệ số tương quan được yêu cầu dễ dàng thu được từ phương trình (14) trong 5.2.2 sử dụng giá trị của s(![]() ,
,![]() ), s(
), s(![]() ,
,![]() ), s(
), s(![]() ,
,![]() ) được tính từ phương trình (17) trong 5.2.3. Các kết quả được cho trong Bảng H.2, trong đó cân nhắc lại là r(xi,xj) = r(xj,xi) và r(xi,xi) = 1.
) được tính từ phương trình (17) trong 5.2.3. Các kết quả được cho trong Bảng H.2, trong đó cân nhắc lại là r(xi,xj) = r(xj,xi) và r(xi,xi) = 1.
Bảng H.2 – Giá trị của đại lượng đầu vào V, I và Ø thu được từ 5 tập hợp quan trắc đồng thời
|
Số tập hợp |
Đại lượng đầu vào |
||
|
V |
I |
Ø |
|
|
1 2 3 4 5 |
5,007 4,994 5,005 4,990 4,999 |
19,663 19,639 19,640 19,685 19,678 |
1,045 6 1,043 8 1,046 8 1,042 8 1,043 3 |
|
Trung bình cộng |
|
|
|
|
Độ lệch chuẩn thực nghiệm của trung bình |
s( |
s( |
s( |
|
Hệ số tương quan |
|||
|
r( r( r( |
|||
H.2.3. Kết quả: cách 1
Bảng H.3 tổng hợp cách 1.
Giá trị của ba đại lượng đo R, X và Z thu được từ mối quan hệ được nêu trong phương trình (H.7) sử dụng giá trị trung bình ![]() ,
, ![]() và
và ![]() của Bảng H.2 đối với V, I và Ø. Độ không đảm bảo chuẩn của R, X và Z thu được từ phương trình (16) trong 5.2.2 do, đã chỉ ra ở trên, đại lượng đầu vào
của Bảng H.2 đối với V, I và Ø. Độ không đảm bảo chuẩn của R, X và Z thu được từ phương trình (16) trong 5.2.2 do, đã chỉ ra ở trên, đại lượng đầu vào ![]() ,
, ![]() và
và ![]() có tương quan. Ví dụ, xét Z =
có tương quan. Ví dụ, xét Z = ![]() /
/ ![]() . Đặt
. Đặt ![]() là x1,
là x1, ![]() là x2 và f là Z =
là x2 và f là Z = ![]() /
/ ![]() , phương trình (16) trong 5.2.2 thu được độ không đảm bảo chuẩn tổng hợp của Z:
, phương trình (16) trong 5.2.2 thu được độ không đảm bảo chuẩn tổng hợp của Z:
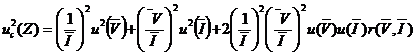 (H.8a)
(H.8a)
![]() (H.8b)
(H.8b)
Hoặc
![]() (H.8c)
(H.8c)
Trong đó ![]() ,
, ![]() , chỉ số dưới “r” trong biểu thức cuối có nghĩa u là độ không đảm bảo tương đối. Thay thế các giá trị thích hợp trong Bảng H.2 vào phương trình (H.8a) cho uc(Z) = 0,236 Ω.
, chỉ số dưới “r” trong biểu thức cuối có nghĩa u là độ không đảm bảo tương đối. Thay thế các giá trị thích hợp trong Bảng H.2 vào phương trình (H.8a) cho uc(Z) = 0,236 Ω.
Vì ba đại lượng đo hay đại lượng đầu ra phụ thuộc vào các đại lượng đầu vào giống nhau nên chúng cũng có tương quan. Các phần tử của ma trận hiệp phương sai mô tả sự tương quan này có thể được viết chung là:
![]() (H.9)
(H.9)
Trong đó yℓ = fℓ(x1, x2, …, xN) và ym = fm(x1, x2, …, xN). Phương trình (H.9) là sự tổng quát hóa của phương trình (F.2) trong F.1.2.3 khi qℓ trong biểu thức đó có tương quan. Hệ số tương quan ước lượng của đại lượng đầu ra được cho bởi r(yℓ,ym) = u(yℓ,ym)/u(yℓ)u(ym) như được trình bày trong phương trình (14) ở 5.2.2. Cần coi các phần tử đường chéo của ma trận hiệp phương sai u(yℓ,ym) ≡ u2(yℓ) là phương sai ước lượng của đại lượng đầu ra yℓ (xem 5.2.2, Chú thích 2) và đối với m = ℓ, phương trình (H.9) giống với phương trình (16) trong 5.2.2.
Để áp dụng phương trình (H.9) vào ví dụ này, đặt như sau:
y1 = R x1 = ![]() u(xi) = s(xi)
u(xi) = s(xi)
y2 = X x2 = ![]() N = 3
N = 3
y3 = Z x3 = ![]()
Kết quả phép tính của R, X, Z và phương sai ước lượng, hệ số tương quan của chúng được cho trong Bảng H.3.
Bảng H.3 – Giá trị tính được của các đại lượng đầu ra R, X và Z: cách 1
|
Chỉ số đại lượng đo |
Mối quan hệ giữa ước lượng của đại lượng đo yℓ và ước lượng đầu vào xi |
Giá trị của ước lượng yℓ, là kết quả đo |
Độ không đảm bảo chuẩn tổng hợp uc(yℓ) của kết quả đo |
|
1 |
y1 = R = |
y1 = R = 127,732 Ω |
uc(R) = 0,071 Ω uc(R)/R = 0,06 x 10-2 |
|
2 |
y2 = R = |
y2 = X = 219,847 Ω |
uc(X) = 0,295 Ω uc(X)/X = 0,13 x 10-2 |
|
3 |
y3 = Z = |
y3 = Z = 254,260 Ω |
uc(Z) = 0,236 Ω uc(Z)/Z = 0,09 x 10-2 |
|
Hệ thống tương quan r(yℓ,ym) |
|||
|
r(y1,y2) = r(R,X) = -0,588 r(y1,y3) = r(R,Z) = -0,485 r(y2,y3) = r(X,Z) = 0,993 |
|||
H.2.4. Kết quả: cách 2
Bảng H.4 tổng hợp cách 2.
Vì dữ liệu thu được là tập hợp năm quan trắc của ba đại lượng đầu vào V, I và Ø nên có thể tính toán giá trị R, X và Z từ từng tập hợp dữ liệu đầu vào, sau đó lấy trung bình cộng của năm giá trị riêng lẻ để thu được ước lượng tốt nhất của R, X và Z. Tính độ lệch chuẩn thực nghiệm của từng trung bình (là độ không đảm bảo chuẩn tổng hợp của nó) từ năm giá trị riêng lẻ theo cách thông thường [phương trình (5) trong 4.2.3]; và sau đó tính hiệp phương sai ước lượng của ba trung bình đó bằng cách áp dụng trực tiếp phương trình (17) trong 5.2.3 cho năm giá trị riêng lẻ, từ đó thu được từng trung bình. Không có sự khác nhau trong các giá trị đầu ra, độ không đảm bảo chuẩn và hiệp phương sai ước lượng thu được từ hai cách ngoại trừ ảnh hưởng bậc hai gắn với việc thay số hạng như ![]() và cos
và cos![]() bằng
bằng ![]() và cos
và cos![]() .
.
Để chứng minh cách tiếp cận này, Bảng H.4 đưa ra các giá trị R, X và Z được tính từ từng tập hợp trong các tập hợp năm quan trắc. Tính trực tiếp trung bình cộng, độ không đảm bảo chuẩn và hệ số tương quan ước lượng từ các giá trị riêng lẻ này. Các kết quả bằng số thu được theo cách này sai khác không đáng kể so với kết quả đưa ra trong Bảng H.3.
Bảng H.4 – Giá trị tính được của các đại lượng đầu ra R, X và Z: cách tiếp cận 1
|
Số tập hợp |
Giá trị riêng lẻ của đại lượng đo |
||
|
R = (V/I)cosØ |
X = (V/I)sinØ |
Z = V/I |
|
|
1 2 3 4 5 |
127,67 127,89 127,51 127,71 127,88 |
220,32 219,79 220,64 218,97 219,51 |
254,64 254,29 254,84 253,49 254,04 |
|
Trung bình cộng Độ lệch chuẩn thực nghiệm của trung bình |
y1 = s( |
y2 = s( |
y3 = s( |
|
Hệ số tương quan r(yℓ,ym) |
|||
|
r(y1,y2) = r( r(y1,y3) = r( r(y2,y3) = r( |
|||
Theo cách ký hiệu ở Chú thích của 4.1.4, cách 2 là ví dụ của việc thu được ước lượng y từ ![]()
![]() , trong khi cách 1 là ví dụ của việc thu được y từ y = f(
, trong khi cách 1 là ví dụ của việc thu được y từ y = f(![]() . Như đã trình bày trong chú thích đó, nói chung, hai cách tiếp cận sẽ cho các kết quả giống nhau nếu f là hàm tuyến tính của các đại lượng đầu vào (với điều kiện có tính đến hệ số tương quan quan trắc được từ thực nghiệm khi tiến hành cách 1). Nếu f không phải là hàm tuyến tính, thì các kết quả của cách 1 sẽ khác với kết quả của cách 2 tùy thuộc vào mức độ phi tuyến, phương sai ước lượng và hiệp phương sai của Xi. Điều này có thể thấy từ biểu thức sau:
. Như đã trình bày trong chú thích đó, nói chung, hai cách tiếp cận sẽ cho các kết quả giống nhau nếu f là hàm tuyến tính của các đại lượng đầu vào (với điều kiện có tính đến hệ số tương quan quan trắc được từ thực nghiệm khi tiến hành cách 1). Nếu f không phải là hàm tuyến tính, thì các kết quả của cách 1 sẽ khác với kết quả của cách 2 tùy thuộc vào mức độ phi tuyến, phương sai ước lượng và hiệp phương sai của Xi. Điều này có thể thấy từ biểu thức sau:
![]() (H.10)
(H.10)
Trong đó số hạng thứ hai của vế phải là số hạng bậc hai trong phép khai triển chuỗi Taylor của f đối với ![]() (Xem thêm 5.1.2, chú thích). Trong trường hợp này, cách tiếp cận 2 được ưu tiên vì tránh được phép tính gần đúng y = f(
(Xem thêm 5.1.2, chú thích). Trong trường hợp này, cách tiếp cận 2 được ưu tiên vì tránh được phép tính gần đúng y = f(![]() và phản ánh tốt hơn thủ tục đo được sử dụng – dữ liệu được thu thập thực tế theo các tập hợp.
và phản ánh tốt hơn thủ tục đo được sử dụng – dữ liệu được thu thập thực tế theo các tập hợp.
Mặt khác, cách tiếp cận 2 là không thích hợp nếu dữ liệu của Bảng H.2 thể hiện n1 = 5 quan trắc hiệu điện thế V, tiếp theo là n2 = 5 quan trắc dòng điện I, n3 = 5 quan trắc pha Ø, sẽ không khả thi nếu n1 # n2 # n3. (Trong thực tế thủ tục đo không hoàn hảo để tiến hành được phép đo theo cách này vì hiệu điện thế đi qua trở kháng cố định và dòng điện qua đó có liên quan trực tiếp.)
Nếu dữ liệu của Bảng H.2 được giải thích lại theo cách này thì cách tiếp cận 2 là không thích hợp và nếu sự tương quan giữa các đại lượng V, I và Ø được giả định là không có thì hệ số tương quan quan trắc được không có ý nghĩa và cần đặt bằng “không”. Nếu điều này được thực hiện trong Bảng H.2 thì phương trình (H.9) rút gọn về tương đương với phương trình (F.2) trong F.1.2.3, nghĩa là:
![]() (H.11)
(H.11)
Và việc áp dụng nó cho dữ liệu của Bảng H.2 dẫn đến sự thay đổi trong Bảng H.3 như được trình bày trong Bảng H.5.
Bảng H.5 – Sự thay đổi trong Bảng H.3 khi giả định hệ số tương quan của Bảng H.2 bằng “không”
|
Độ không đảm bảo chuẩn uc(yℓ) của kết quả đo |
|
uc(R) = 0,195 Ω uc(R)/R = 0,15 x 10-2 |
|
uc(X) = 0,201 Ω uc(X)/X = 0,09 x 10-2 |
|
uc(Z) = 0,204 Ω uc(Z)/Z = 0,08 x 10-2 |
|
Hệ số tương quan r(yℓ,ym) |
|
r(y1,y2) = r(R,X) = 0,056 r(y1,y3) = r(R,Z) = 0,527 r(y2,y3) = r(X,Z) = 0,878 |
H.3. Hiệu chuẩn nhiệt kế
Ví dụ này minh họa việc sử dụng phương pháp bình phương tối thiểu để nhận được đường cong hiệu chuẩn tuyến tính và cách sử dụng các tham số làm khớp, phần chặn và độ dốc, phương sai và hiệp phương sai ước lượng của chúng để thu được giá trị và độ không đảm bảo chuẩn của sự hiệu chính dự đoán từ đường cong đó.
H.3.1. Vấn đề của phép đo
Nhiệt kế được hiệu chuẩn bằng cách so sánh n = 11 số đọc nhiệt độ tk của nhiệt kế, mỗi số đọc có độ không đảm bảo không đáng kể, với nhiệt độ chuẩn đã biết tương ứng tR,k trong dải nhiệt độ từ 210C đến 270C để nhận được số hiệu chính bk = tR,k – tk cho các số đọc. Sự hiệu chính đo được bk và nhiệt độ đo được tk là các đại lượng đầu vào của đánh giá. Đường cong hiệu chuẩn tuyến tính:
bt = y1 + y2(t – t0) (H.12)
được làm khớp với sự hiệu chính và nhiệt độ đo được bằng phương pháp bình phương tối thiểu. Tham số y1 và y2, tương ứng là phần chặn và độ dốc của đường cong hiệu chuẩn, là hai đại lượng đo hoặc đại lượng đầu ra cần được xác định. Nhiệt độ to là nhiệt độ quy chiếu chính xác được chọn thích hợp; nó không phải là tham số độc lập được xác định bằng cách làm khớp bình phương tối thiểu. Khi tìm được y1 và y2, cùng với phương sai và hiệp phương sai ước lượng của chúng, có thể sử dụng phương trình (H.12) để dự báo giá trị và độ không đảm bảo chuẩn của sự hiệu chính được áp dụng cho nhiệt kế đối với mọi giá trị t của nhiệt độ.
H.3.2. Sự khớp bình phương tối thiểu
Dựa trên phương pháp bình phương tối thiểu và với các giả định được nêu ở H.3.1, đại lượng đầu ra y1 và y2, phương sai và hiệp phương sai ước lượng của chúng nhận được bằng cách làm cực tiểu tổng
![]()
Điều này dẫn đến phương trình sau đây cho y1, y2, phương sai thực nghiệm s2(y1) và s2(y2), hệ số tương quan ước lượng của chúng r(y1,y2) = s(y1,y2)/s(y1)s(y2), trong đó s(y1,y2) là hiệp phương sai ước lượng của chúng:
![]() (H.13a)
(H.13a)
![]() (H.13b)
(H.13b)
![]() (H.13c)
(H.13c)
![]() (H.13d)
(H.13d)
 (H.13e)
(H.13e)
![]() (H.13f)
(H.13f)
![]() (H.13g)
(H.13g)
Trong đó tất cả các tổng là từ k = 1 đến n, θk = tk – to, ![]() ; và
; và ![]() ; [bk – b(tk)] là chênh lệch giữa sự hiệu chính đo được hoặc quan trắc được bk ở nhiệt độ tk và sự hiệu chính b(tk) được dự đoán bằng đường cong được làm khớp b(t) = y1 + y2(t – to) ở tk. Phương sai s2 là thước đo của độ không đảm bảo tổng thể của việc làm khớp, trong đó thừa số n – 2 phản ảnh thực tế do hai tham số y1 và y2, được xác định bằng n quan trắc nên bậc tự do của s2 là v = n – 2 (xem G.3.3).
; [bk – b(tk)] là chênh lệch giữa sự hiệu chính đo được hoặc quan trắc được bk ở nhiệt độ tk và sự hiệu chính b(tk) được dự đoán bằng đường cong được làm khớp b(t) = y1 + y2(t – to) ở tk. Phương sai s2 là thước đo của độ không đảm bảo tổng thể của việc làm khớp, trong đó thừa số n – 2 phản ảnh thực tế do hai tham số y1 và y2, được xác định bằng n quan trắc nên bậc tự do của s2 là v = n – 2 (xem G.3.3).
H.3.3. Tính toán các kết quả
Dữ liệu được làm khớp cho trong cột thứ hai và ba của Bảng H.6. Lấy t0 = 200C là nhiệt độ quy chiếu, áp dụng phương trình (H.13a) vào (H.13g) thu được:
y1 = -0,171 20C s(y1) = 0,002 90C
y2 = 0,002 18 s(y2) = 0,000 67
r(y1,y2) = -0,930 s = 0,003 50C
Thực tế là độ dốc y2 lớn gấp ba lần so với độ không đảm bảo chuẩn của nó cung cấp một số chỉ báo rằng đường cong hiệu chuẩn chứ không phải sự hiệu chính trung bình cố định được yêu cầu.
Bảng H.6 – Dữ liệu được sử dụng để thu được đường cong hiệu chuẩn tuyến tính của nhiệt kế bằng phương pháp bình phương tối thiểu
|
Số phép đọc |
Số đọc nhiệt kế |
Số hiệu chính quan trắc được |
Số hiệu chính dự đoán |
Chênh lệch giữa số hiệu chính quan trắc được và dự đoán |
|
1 2 3 4 5 6 7 8 9 10 11 |
21,521 22,012 22,512 23,003 23,507 23,999 24,513 25,002 25,503 26,010 26,511 |
-0,171 -0,169 -0,166 -0,159 -0,164 -0,165 -0,156 -0,157 -0,159 -0,161 -0,160 |
-0,167 9 -0,166 8 -0,165 7 -0,164 6 -0,163 5 -0,162 5 -0,161 4 -0,160 3 -0,159 2 -0,158 1 -0,157 0 |
-0,003 1 -0,002 2 -0,000 3 +0,005 6 -0,000 5 -0,002 5 +0,005 4 +0,003 3 +0,000 2 -0,002 9 -0,003 0 |
Đường cong hiệu chuẩn khi đó có thể viết là:
b(t) = 0,171 2(29)0C + 0,002 18(67)(t – 200C) (H.14)
Trong đó các số trong ngoặc đơn là trị số của độ không đảm bảo chuẩn là các chữ số cuối cùng tương ứng của kết quả được trích dẫn đối với phần chặn và độ dốc (xem 7.2.2). Phương trình này đưa ra giá trị dự đoán của số hiệu chính b(t) ở nhiệt độ t bất kỳ và cụ thể giá trị b(tk) ở t = tk. Các giá trị này được nêu trong cột thứ tư của bảng trong khi cột cuối cùng đưa ra chênh lệch giữa các giá trị đo được và dự đoán, bk – b(tk). Có thể sử dụng phép phân tích các chênh lệch này để kiểm tra giá trị của mô hình tuyến tính; có các phép thử chính thức (xem Tài liệu tham khảo [8] nhưng không được xem xét trong ví dụ này.
H.3.4. Độ không đảm bảo của giá trị dự đoán
Biểu thức cho độ không đảm bảo chuẩn tổng hợp của giá trị dự đoán của sự hiệu chính có thể thu được dễ dàng bằng cách áp dụng định luật lan truyền độ không đảm bảo, phương trình (16) trong 5.2.2, vào phương trình (H.12). Chú ý b(t) = f(y1,y2) và đặt u(y1) = s(y1) và u(y2) = s(y2), sẽ thu được:
![]() (H.15)
(H.15)
Phương sai ước lượng ![]() là giá trị cực tiểu ở tmin = to =
là giá trị cực tiểu ở tmin = to = ![]() , trong trường hợp này là tmin = 24,008 50C.
, trong trường hợp này là tmin = 24,008 50C.
Xét một ví dụ về sử dụng phương tình (H.15), ta xem là cần có số hiệu chính nhiệt kế và độ không đảm bảo của nó ở t = 300C, nằm ngoài dải nhiệt độ mà nhiệt kế đã được hiệu chuẩn thực tế. Thay t = 300C vào phương trình (H.14) cho ra
b(300C) = – 0,149 40C
Trong khi đó phương trình (H.15) trở thành:
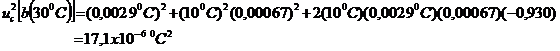
Hoặc
uc[b(300C)] = 0,004 10C
Do đó số hiệu chính ở 300C là -0,149 40C với độ không đảm bảo chuẩn tổng hợp uc = 0,004 10C và với uc có bậc tự do v = n – 2 = 9.
H.3.5. Loại trừ tương quan giữa độ dốc và phần chắn
Phương trình (H.13e) với hệ số tương quan r(y1,y2) hàm ý nếu t0 được chọn để ![]() thì r(y1,y2) = 0 và y1, y2 sẽ không tương quan, do đó làm đơn giản hóa phép tính độ không đảm bảo chuẩn của số hiệu chính dự đoán. Do
thì r(y1,y2) = 0 và y1, y2 sẽ không tương quan, do đó làm đơn giản hóa phép tính độ không đảm bảo chuẩn của số hiệu chính dự đoán. Do ![]() khi
khi ![]() và trong trường hợp này
và trong trường hợp này![]() = 24,008 50C, nên lặp lại việc làm khớp bình phương tối thiểu với
= 24,008 50C, nên lặp lại việc làm khớp bình phương tối thiểu với ![]() sẽ dẫn đến giá trị y1 và y2 không tương quan. (Nhiệt độ
sẽ dẫn đến giá trị y1 và y2 không tương quan. (Nhiệt độ ![]() cũng là nhiệt độ mà ở đó u2[b(t)] là nhỏ nhất – xem H.3.4.) Tuy nhiên, việc làm khớp lặp lại là không cần thiết vì nó có thể được chỉ ra rằng:
cũng là nhiệt độ mà ở đó u2[b(t)] là nhỏ nhất – xem H.3.4.) Tuy nhiên, việc làm khớp lặp lại là không cần thiết vì nó có thể được chỉ ra rằng:
b(t) = y’1 + y2(t – ![]() ) (H.16a)
) (H.16a)
![]() (H.16b)
(H.16b)
r(y’1,y2) = 0 (H.16c)
trong đó:
y’1 = y1 + y2(![]() – t0)
– t0)
![]() = to – s(y1) r(y1,y2)/s(y2)
= to – s(y1) r(y1,y2)/s(y2)
s2(y’1) = s2(y1)[1 – r2(y1,y2)]
Và khi viết phương trình (H.16b), việc thay u(y’1) = s(y’1) và u(y2) = s(y2) đã được thực hiện [xem phương trình (H.15)].
Áp dụng các quan hệ này vào kết quả được cho trong H.3.3 thu được:
b(t) = -0,162 5(11) + 0,002 18(67)(t – 24,008 50C) (H.17a)
![]() (0,001 1)2 + (t – 24,008 50C)2(0,000 67)2 (H.17b)
(0,001 1)2 + (t – 24,008 50C)2(0,000 67)2 (H.17b)
Các biểu thức này cho ra kết quả giống như phương trình (H.14) và (H.15) có thể kiểm tra bằng cách lặp lại phép tính b(300C) và uc[b(300C)]. Thay t = 300C vào phương trình (H.17a) và (H.17b) thu được:
b(300C) = -0,149 40C
uc[b(300C)] = 0,004 10C.
Bằng với kết quả thu được trong H.3.4. hiệp phương sai ước lượng giữa hai số hiệu chính dự đoán b(t1) và b(t2) có thể thu được từ phương trình (H.9) trong H.2.3.
H.3.6. Các xem xét khác
Phương pháp bình phương tối thiểu có thể được sử dụng để làm khớp đường cong bậc cao hơn với các điểm dữ liệu và cũng có thể áp dụng cho trường hợp các điểm dữ liệu riêng lẻ có độ không đảm bảo. Nội dung tiêu chuẩn về vấn đề này cần tham khảo chi tiết [8]. Tuy nhiên, các ví dụ sau minh họa cho hai trường hợp trong đó giả định là không biết chính xác giá trị hiệu chính đo được bk.
1) Cho từng tk có độ không đảm bảo không đáng kể, cho từng giá trị của n giá trị tR,k thu được từ loạt m số đọc lặp lại và cho ước lượng tích lũy của phương sai đối với các số đọc này dựa trên lượng lớn dữ liệu thu được trong nhiều tháng là ![]() . Khi đó, phương sai ước lượng của từng tR,k là
. Khi đó, phương sai ước lượng của từng tR,k là![]() và từng số hiệu chính quan trắc được bk = tR,k – tk có cùng độ không đảm bảo chuẩn uo. Trong những tình huống này (và giả định rằng không có lý do để tin rằng mô hình tuyến tính là không đúng),
và từng số hiệu chính quan trắc được bk = tR,k – tk có cùng độ không đảm bảo chuẩn uo. Trong những tình huống này (và giả định rằng không có lý do để tin rằng mô hình tuyến tính là không đúng), ![]() thay cho s2 trong phương trình (H.13c) và (H.13d).
thay cho s2 trong phương trình (H.13c) và (H.13d).
CHÚ THÍCH: Ước lượng tích lũy của phương sai ![]() dựa trên N dãy các quan trắc độc lập của cùng một biến ngẫu nhiên thu được từ:
dựa trên N dãy các quan trắc độc lập của cùng một biến ngẫu nhiên thu được từ:
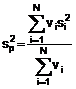
Trong đó ![]() là phương sai thực nghiệm của dãy thứ i có ni quan trắc lặp lại độc lập [phương trình 4 trong 4.2.2] và có bậc tự do vi = ni – 1. Bậc tự do của
là phương sai thực nghiệm của dãy thứ i có ni quan trắc lặp lại độc lập [phương trình 4 trong 4.2.2] và có bậc tự do vi = ni – 1. Bậc tự do của ![]() là v =
là v = ![]() . Phương sai thực nghiệm
. Phương sai thực nghiệm ![]() /m (và độ lệch chuẩn thực nghiệm
/m (và độ lệch chuẩn thực nghiệm ![]() /
/![]() ) của trung bình cộng của m quan trắc độc lập được đặc trưng bởi ước lượng tích lũy của phương sai
) của trung bình cộng của m quan trắc độc lập được đặc trưng bởi ước lượng tích lũy của phương sai ![]() cùng có v bậc tự do.
cùng có v bậc tự do.
2) Giả sử rằng mỗi tk có độ không đảm bảo không đáng kể, sự hiệu chính εk được áp dụng cho từng giá trị của n giá trị tR,k và mỗi số hiệu chính có cùng độ không đảm bảo chuẩn ua. Khi đó độ không đảm bảo chuẩn của từng bk = tR,k – tk cũng là ua và s2(y1) được thay bằng s2(y1) + ![]() và s2(y’1) được thay bằng s2(y’1) +
và s2(y’1) được thay bằng s2(y’1) + ![]() .
.
H.4. Phép đo độ phóng xạ
Ví dụ này tương tự ví dụ ở H.2, phép đo điện trở và điện kháng đồng thời, trong đó có thể phân tích dữ liệu theo hai cách khác nhau nhưng cho kết quả về cơ bản giống nhau. Cách thứ nhất minh họa lại một lần nữa sự cần thiết phải đưa sự tương quan giữa các đại lượng đầu vào quan trắc được vào tính toán.
H.4.1. Nồng độ phóng xạ cua rađon (222Rn) trong mẫu nước được xác định bằng cách đếm sự phát sáng lỏng so với mẫu chuẩn rađon trong nước có nồng độ phóng xa đã biết. Nồng độ phóng xạ chưa biết thu được bằng cách đo ba nguồn đếm có khoảng 5 g nước và 12 g chất phát sáng nhũ tương hữu cơ trong các lọ có thể tích 22 ml.
|
Nguồn (a) |
chuẩn có khối lượng dung dịch chuẩn ms với nồng độ phóng xạ biết; |
|
Nguồn (b) |
mẫu nước trắng phù hợp không chứa vật liệu phóng xạ, được sử dụng để thu được tốc độ đếm nền; |
|
Nguồn (c) |
một mẫu có khối lượng mx với nồng độ phóng xạ chưa biết. |
Sáu chu kỳ đo của ba nguồn đếm được thực hiện theo thứ tự chuẩn – mẫu trắng – mẫu; mỗi khoảng thời gian đếm đã hiệu chính thời gian chết To cho từng nguồn trong cả sáu chu kỳ là 60 phút. Mặc dù không thể giả định tốc độ đếm nền là không đổi trong toàn bộ khoảng đếm (65 giờ), nhưng được giả định rằng số lần đếm thu được đối với từng mẫu trắng có thể được sử dụng làm đại diện của vận tốc đếm nền trong toàn bộ phép đo chuẩn và mẫu trong cùng chu kỳ. Bảng H.7 cho các dữ liệu, trong đó:
|
tS, tB, tx |
là thời gian tình từ thời gian quy chiếu t = 0 đến điểm giữa của khoảng thời gian đếm đã hiệu chính thời gian chết To = 60 min tương ứng đối với bình chuẩn, mẫu trắng và mẫu; mặc dù tB được cho để đầy đủ nhưng không cần sử dụng trong phân tích; |
|
CS, CB, Cx |
là số lần đếm được ghi lại trong khoảng thời gian đếm đã hiệu chính thời gian chết To = 60 min tương ứng đối với chuẩn, mẫu trắng và mẫu. |
Các phép đếm quan trắc được có thể được thể hiện như sau:
![]() (H.18a)
(H.18a)
![]() (H.18b)
(H.18b)
Trong đó:
|
ε |
là năng suất phát hiện sự phát sáng chất lỏng của 222Rn đối với thành phần nguồn đã cho, được giả định là độc lập với mức phóng xạ; |
|
AS |
là nồng độ phóng xạ của chuẩn ở thời điểm quy chiếu t = 0; |
|
Ax |
là đại lượng đo và được xác định là nồng độ phóng xạ chưa biết của mẫu ở thời gian quy chiếu t = 0; |
|
mS |
là khối lượng của dung dịch chuẩn; |
|
mx |
là khối lượng của mẫu; |
|
l |
là hằng số phân rã của 222Rn: l = (ln2)/T1/2 = 1,258 94 x 10-4 min-1 (T1/2 = 5 505,8 min) |
Bảng H.7 – Dữ liệu đếm để xác định nồng độ phóng xạ của mẫu chưa biết
|
Chu trình |
Chuẩn |
Mẫu trắng |
Mẫu |
|||
|
k |
ts |
Cs |
tB |
CB |
tx |
Cx |
|
1 |
243,74 |
15 380 |
305,56 |
4 054 |
367,37 |
41 432 |
|
2 |
984,53 |
14 978 |
1 046,10 |
3 922 |
1 107,66 |
38 706 |
|
3 |
1 723,87 |
14 394 |
1 785,43 |
4 200 |
1 846,99 |
35 860 |
|
4 |
2 463,17 |
13 254 |
2 524,73 |
3 830 |
2 586,28 |
32 238 |
|
5 |
3 217,56 |
12 516 |
3 279,12 |
3 956 |
3 340,68 |
29 640 |
|
6 |
3 956,83 |
11 058 |
4 018,38 |
3 980 |
4 079,94 |
26 356 |
Phương trình (H.18a) và (H.18b) chỉ ra rằng sáu giá trị riêng lẻ của CS hay Cx được cho trong Bảng H.7 không thể tính trung bình trực tiếp vì sự phân rã dạng hàm mũ độ phóng xạ của chuẩn và mẫu, và sự biến động nhẹ đếm nền từ chu trình này đến chu trình kia. Thay vào đó, ta phải giải quyết các phép đếm phân rã được hiệu chính và các phép đếm nền được hiệu chính (hoặc tốc độ đếm được xác định là số phép đếm chia cho To = 60 min). Điều này đề xuất kết hợp phương trình (H.18a) và (H.18b) đê thu được biểu thức sau đây cho nồng độ chưa biết theo các đại lượng đã biết:
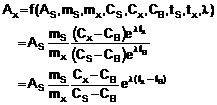 (H.19)
(H.19)
Trong đó ![]() và
và ![]() tương ứng là phép đếm nền được hiệu chính của mẫu và chuẩn ở thời gian quy chiếu t = 0 và với khoảng thời gian T0 = 60 min. Ngoài ra, có thể viết đơn giản là:
tương ứng là phép đếm nền được hiệu chính của mẫu và chuẩn ở thời gian quy chiếu t = 0 và với khoảng thời gian T0 = 60 min. Ngoài ra, có thể viết đơn giản là:
![]() (H.20)
(H.20)
Trong đó tốc độ đếm nền được hiệu chính và tốc độ đếm phân rã được hiệu chính Rx và RS được cho bằng:
![]() (H.21a)
(H.21a)
![]() (H.21b)
(H.21b)
H.4.2. Phân tích dữ liệu
Bảng H.8 tổng kết các giá trị của tốc độ đếm nền được hiệu chính và tốc độ đếm phân rã được hiệu chính RS và Rx được tính từ phương trình (H.21a) và (H.21b) sử dụng dữ liệu của Bảng H.7 và l = 1,258 94 x 10-4 min-1 như được cho ở trên. Cần chú ý rằng tỉ số R = Rx/RS được tính đơn giản nhất từ công thức:
![]()
Các trung bình cộng ![]() và độ lệch chuẩn thực nghiệm của chúng s(
và độ lệch chuẩn thực nghiệm của chúng s(![]() ), s(
), s(![]() ), s(
), s(![]() ) được tính theo cách thông thường [phương trình (3) và (5) trong 4.2]. Tính hệ số tương quan r(
) được tính theo cách thông thường [phương trình (3) và (5) trong 4.2]. Tính hệ số tương quan r(![]() ,
,![]() ) được tính từ phương trình (17) trong 5.2.3 và phương trình (14) trong 5.2.2.
) được tính từ phương trình (17) trong 5.2.3 và phương trình (14) trong 5.2.2.
Vì độ biến thiên nhỏ so sánh được của giá trị Rx và RS nên tỉ số của trung bình ![]() /
/![]() và độ không đảm bảo chuẩn u(
và độ không đảm bảo chuẩn u(![]() /
/![]() ) của tỉ số này gần như bằng, tương ứng, tỉ số trung bình
) của tỉ số này gần như bằng, tương ứng, tỉ số trung bình ![]() và độ lệch chuẩn thực nghiệm s(
và độ lệch chuẩn thực nghiệm s(![]() ) như cho trong cột cuối cùng của Bảng H.8 [xem H.2.4 và phương trình H.10 trong đó]. Tuy nhiên, trong việc tính độ không đảm bảo chuẩn u(
) như cho trong cột cuối cùng của Bảng H.8 [xem H.2.4 và phương trình H.10 trong đó]. Tuy nhiên, trong việc tính độ không đảm bảo chuẩn u(![]() /
/![]() ), tương quan giữa
), tương quan giữa ![]() và
và ![]() như được đại diện bằng hệ số tương quan r(
như được đại diện bằng hệ số tương quan r(![]() ,
,![]() ) phải được tính đến bằng việc sử dụng phương trình (16) trong 5.2.2. [Phương trình đó mang lại cho phương sai ước lượng tương đối với
) phải được tính đến bằng việc sử dụng phương trình (16) trong 5.2.2. [Phương trình đó mang lại cho phương sai ước lượng tương đối với ![]() /
/![]() ba số hạng cuối cùng của phương trình (H.22b).]
ba số hạng cuối cùng của phương trình (H.22b).]
Cần thừa nhận là độ lệch chuẩn thực nghiệm tương ứng của Rx và RS, ![]() và
và ![]() chỉ ra độ biến thiên trong các đại lượng này là lớn hơn từ hai đến ba lần độ biến thiên được bao hàm trong thống kê Poison các quá trình đếm; biến động sau cùng được bao gồm trong độ biến động quan trắc được của phép đếm và không cần tính riêng rẽ.
chỉ ra độ biến thiên trong các đại lượng này là lớn hơn từ hai đến ba lần độ biến thiên được bao hàm trong thống kê Poison các quá trình đếm; biến động sau cùng được bao gồm trong độ biến động quan trắc được của phép đếm và không cần tính riêng rẽ.
Bảng H.8 – Tính độ đếm phân rã được hiệu chính và tốc độ đếm nền được hiệu chính
|
Chu kỳ |
Rx |
RS |
tx – tS |
R = Rx/RS |
|
1 2 3 4 5 6 |
652,46 666,48 665,80 655,68 651,87 623,31 |
194,65 208,58 211,08 214,17 213,92 194,13 |
123,63 123,13 123,12 123,11 123,12 123,11 |
3,352 0 3,195 3 3,154 3 3,061 5 3,047 3 3,210 7 |
|
|
|
|
|
|
|
|
||||
|
Hệ số tương quan |
||||
|
r( |
||||
H.4.3. Tính toán kết quả cuối cùng
Để thu được nồng độ phóng xạ chưa biết Ax và độ không đảm bảo chuẩn tổng hợp uc(Ax) từ phương trình (H.20) cần biết AS, mx, mS và độ không đảm bảo chuẩn của chúng. Chúng được cho như sau:
As = 0,136 8 Bq/g;
u(As) = 0,001 8 Bq/g; u(AS)/AS = 1,32 x 10-2
mS = 5,019 2g
u(mS) = 0,005 0 g; u(mS)/mS = 0,10 x 10-2
mx = 5,057 1g
u(mx) = 0,001 0 g; u(mx)/mx = 0,02 x 10-2
Các nguồn khác của độ không đảm bảo có thể có được đánh giá là không đáng kể:
– độ không đảm bảo chuẩn của số lần phân rã, u(tS,k) và u(tx,k);
– độ không đảm bảo chuẩn của hằng số phân rã của 222Rn, u(l) = 1 x 10-7 min-1. (Đại lượng có ý nghĩa là thừa số phân rã exp[l(tx – tS)], biến thiên từ 1,015 63 đối với chu kỳ k = 4 và 6 tới 1,01570 đối với chu kỳ k = 1. Độ không đảm bảo chuẩn của các giá trị này là u = 1,2×10-5);
– độ không đảm bảo gắn với sự phụ thuộc có thể có của hiệu suất phát hiện của thiết bị đếm sự phát sáng trên nguồn được sử dụng (chuẩn, mẫu trắng và mẫu);
– độ không đảm bảo của sự hiệu chính thiết bị đếm thời gian chết và của sự hiệu chính sự phụ thuộc của hiệu suất đếm vào mức phóng xạ.
H.4.3.1. Kết quả: cách tiếp cận 1
Như đã nói ở trên, Ax và uc(Ax) có thể thu được theo hai cách khác nhau từ phương trình (H.20). Ở cách tiếp cận đầu tiên, Ax được tính bằng cách sử dụng trung bình cộng ![]() và
và ![]() , dẫn tới:
, dẫn tới:
![]() (H.22a)
(H.22a)
Việc áp dụng phương trình (16) trong 5.2.2 cho công thức này mang lại đối với phương sai tổng hợp ![]()
![]() (H.22b)
(H.22b)
Trong đó, như đã chú thích trong H.4.2, ba số hạng sau cùng cho ![]()
![]() /
/![]() )/(
)/(![]() /
/![]() )2, phương sai tương đối ước lượng của
)2, phương sai tương đối ước lượng của ![]() /
/![]() ; Phù hợp với thảo luận của H.2.4, các kết quả trong Bảng H.8 chỉ ra rằng
; Phù hợp với thảo luận của H.2.4, các kết quả trong Bảng H.8 chỉ ra rằng ![]() không đúng bằng
không đúng bằng ![]() /
/![]() ; và độ không đảm bảo chuẩn u(
; và độ không đảm bảo chuẩn u(![]() /
/![]() ) của
) của ![]() /
/![]() không đúng bằng độ không đảm bảo chuẩn s(
không đúng bằng độ không đảm bảo chuẩn s(![]() ) của
) của ![]() .
.
Thay các giá trị của đại lượng liên quan vào phương trình (H.22a) và (H.22b) mang lại:
![]()
uc(Ax) = 0,008 3 Bq/g
Kết quả đo khi đó có thể được công bố là:
Ax = 0,430 0 Bq/g với độ không đảm bảo chuẩn tổng hợp uc = 0,008 3 Bq/g.
H.4.3.2. Kết quả: cách tiếp cận 2
Trong cách tiếp cận thứ hai, tránh được sự tương quan giữa ![]() và
và ![]() , Ax được tính bằng cách sử dụng trung bình cộng
, Ax được tính bằng cách sử dụng trung bình cộng ![]() . Do đó
. Do đó
![]() (H.23a)
(H.23a)
Biểu thức cho ![]() đơn giản là:
đơn giản là:
![]() (H.23b)
(H.23b)
Suy ra:
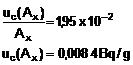
Khi đó, kết quả đo có thể được trình bày như sau:
Ax = 0,430 4 Bq/g với độ không đảm bảo chuẩn tổng hợp uc = 0,008 4 Bq/g.
Bậc tự do hiệu dụng của uc có thể được đánh giá bằng công thức Welch-Satterthwaite theo cách được minh họa trong H.1.6.
Như trong H.2, trong hai kết quả, kết quả thứ hai được ưu tiên hơn vì nó tránh tính xấp xỉ trung bình của tỉ số hai đại lượng bằng tỉ số của trung bình của hai đại lượng đó; và nó phản ánh tốt hơn thủ tục đo đã được sử dụng – dữ liệu được thu thập thực tế trong các chu kỳ riêng biệt.
Tuy nhiên, chênh lệch giữa các giá trị của Ax do hai cách tiếp cận rõ ràng là nhỏ so với độ không đảm bảo chuẩn được gán cho một trong hai và sự khác nhau giữa hai độ không đảm bảo chuẩn là hoàn toàn không đáng kể. Sự thống nhất này chứng tỏ hai cách tiếp cận là tương đương khi sự tương quan quan trắc được tính đến một cách phù hợp.
H.5. Phân tích phương sai
Ví dụ này đưa ra giới thiệu ngắn gọn về các phương pháp phân tích phương sai (ANOVA). Các kỹ thuật thống kê được sử dụng để xác định và định hướng các ảnh hưởng ngẫu nhiên riêng biệt của phép đo để chúng có thể được tính đến thích đáng khi đánh giá độ không đảm bảo của kết quả đo. Mặc dù phương pháp ANOVA có thể áp dụng cho phạm vi rộng các phép đo, ví dụ, hiệu chuẩn các chuẩn chính như chuẩn điện áp Zener, chuẩn khối lượng và chứng nhận mẫu chuẩn, nhưng bản thân phương pháp ANOVA không thể xác định ảnh hưởng hệ thống có thể có.
Tên gọi chung ANOVA bao gồm nhiều mô hình khác nhau. Vì tầm quan trọng của nó, mô hình cụ thể được thảo luận trong ví dụ này là thiết kế lồng nhau cân bằng. Minh họa bằng số của mô hình này gồm có phép hiệu chuẩn chuẩn điện áp Zener; việc phân tích cần phù hợp với sự thay đổi của các tình huống đo thực tế.
Phương pháp ANOVA đặc biệt quan trọng trong chứng nhận mẫu chuẩn (RM) bằng thử nghiệm liên phòng, đó là chủ đề bao trùm toàn bộ TCVN 8245:2009 (ISO Guide 35) [19] (xem H.5.3.2, mô tả ngắn gọn việc chứng nhận RM như vậy). Do nhiều nội dung trong ISO Guide 35 có thể áp dụng rộng rãi trong thực tế nên có thể tham khảo tiêu chuẩn đó về các chi tiết bổ sung liên quan đến ANOVA, bao gồm các thiết kế lồng nhau không cân bằng. Tương tự có thể tham khảo [15] và [20].
H.5.1. Vấn đề của phép đo
Xét chuẩn điện áp Zener 10 V danh nghĩa được hiệu chuẩn so với điện áp quy chiếu ổn định trong khoảng thời gian hai tuần. Mỗi ngày trong J ngày trong suốt khoảng thời gian này, thực hiện K quan trắc lặp lại độc lập hiệu điện thế VS của chuẩn. Nếu Vjk ký hiệu cho quan trắc thứ k của Vs (k = 1, 2, …, K) ở ngày thứ j (j = 1, 2, …, J) thì ước lượng tốt nhất hiệu điện thế của chuẩn là trung bình cộng V của JK quan trắc [xem phương trình (3) trong 4.2.1]
![]() (H.24a)
(H.24a)
Độ lệch chuẩn thực nghiệm của trung bình s(![]() ), là thước đo độ không đảm bảo của
), là thước đo độ không đảm bảo của ![]() là ước lượng hiệu điện thế của chuẩn, thu được từ [xem phương trình (5) trong 4.2.3]:
là ước lượng hiệu điện thế của chuẩn, thu được từ [xem phương trình (5) trong 4.2.3]:
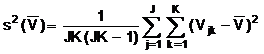 (H.24b)
(H.24b)
CHÚ THÍCH: Giả định trong toàn bộ ví dụ này là tất cả sự hiệu chính đã được áp dụng cho quan trắc để bù các ảnh hưởng hệ thống có độ không đảm bảo không đáng kể hoặc độ không đảm bảo của chúng có thể được tính đến ở cuối phép phân tích. Sự hiệu chính ở loại sau này, và sự hiệu chính có thể được áp dụng cho trung bình của các quan trắc ở cuối phép phân tích, là sự khác nhau giữa các giá trị được chứng nhận (được giả định có độ không đảm bảo đã cho) và giá trị làm việc của điện áp quy chiếu ổn định so với chuẩn điện thế Zener đã được hiệu chuẩn. Do đó ước lượng hiệu điện thế của chuẩn thu được bằng thống kê từ các quan trắc không nhất thiết là kết quả cuối cùng của phép đo; và độ lệch chuẩn thực nghiệm của ước lượng đó không nhất thiết là độ không đảm bảo chuẩn tổng hợp của kết quả cuối cùng.
Độ lệch chuẩn thực nghiệm của trung bình s(![]() ) như thu được từ phương trình (H.24b) là thước đo thích hợp độ không đảm bảo của
) như thu được từ phương trình (H.24b) là thước đo thích hợp độ không đảm bảo của ![]() chỉ khi độ biến thiên từ ngày này sang ngày khác của quan trắc bằng độ biến thiên của các quan trắc được thực hiện trong một ngày. Nếu có bằng chứng rằng độ biến thiên giữa các ngày lớn đáng kể so với độ biến thiên có thể kỳ vọng trong ngày thì việc sử dụng công thức này có thể dẫn tới sự giảm nhẹ đáng kể độ không đảm bảo của
chỉ khi độ biến thiên từ ngày này sang ngày khác của quan trắc bằng độ biến thiên của các quan trắc được thực hiện trong một ngày. Nếu có bằng chứng rằng độ biến thiên giữa các ngày lớn đáng kể so với độ biến thiên có thể kỳ vọng trong ngày thì việc sử dụng công thức này có thể dẫn tới sự giảm nhẹ đáng kể độ không đảm bảo của ![]() . Do đó, hai câu hỏi đặt ra: Cần quyết định thế nào nếu độ biến thiên giữa các ngày (được đặc trưng bằng thành phần phương sai giữa các ngày) là đáng kể khi so với độ biến thiên trong ngày (được đặc trưng bằng thành phần phương sai trong ngày) và, nếu như vậy thì, cần đánh giá độ không đảm bảo của trung bình thế nào?
. Do đó, hai câu hỏi đặt ra: Cần quyết định thế nào nếu độ biến thiên giữa các ngày (được đặc trưng bằng thành phần phương sai giữa các ngày) là đáng kể khi so với độ biến thiên trong ngày (được đặc trưng bằng thành phần phương sai trong ngày) và, nếu như vậy thì, cần đánh giá độ không đảm bảo của trung bình thế nào?
H.5.2. Ví dụ hằng số
H.5.2.1. Bảng H.9 đưa ra các dữ liệu cho việc giải đáp các câu hỏi ở trên, trong đó
J = 10 là số ngày thực hiện các quan trắc hiệu điện thế;
K = 5 là số quan trắc hiệu điện thế được thực hiện trong một ngày;
![]() (H.25a)
(H.25a)
Là trung bình cộng của K = 5 quan trắc hiệu điện thế thực hiện vào ngày thứ j (có J = 10 trung bình theo ngày như vậy):
![]() (H.25b)
(H.25b)
Là trung bình cộng của J = 10 trung bình theo ngày và do đó trung bình tổng thể của JK = 50 quan trắc:
![]() (H.25c)
(H.25c)
Là phương sai thực nghiệm của K = 5 quan trắc được thực hiện vào ngày thứ J (có J = 10 ước lượng phương sai như vậy); và
![]() (H.25d)
(H.25d)
Là phương sai thực nghiệm của J = 10 trung bình theo ngày (chỉ có một ước lượng phương sai như vậy).
H.5.2.2. Tính nhất quán của độ biến thiên trong ngày và độ biến thiên giữa các ngày của các quan trắc có thể được nghiên cứu bằng cách so sánh hai ước lượng độc lập của![]() , thành phần của phương sai trong ngày (nghĩa là, phương sai của các quan trắc được thực hiện trong cùng một ngày).
, thành phần của phương sai trong ngày (nghĩa là, phương sai của các quan trắc được thực hiện trong cùng một ngày).
Ước lượng thứ nhất của![]() , ký hiệu là
, ký hiệu là ![]() , thu được từ phương sai quan trắc được của các trung bình theo ngày
, thu được từ phương sai quan trắc được của các trung bình theo ngày ![]() . Do
. Do ![]() là trung bình của K quan trắc, phương sai ước lượng của nó s2(
là trung bình của K quan trắc, phương sai ước lượng của nó s2(![]() ), ước lượng
), ước lượng ![]() /K, với giả định là thành phần phương sai giữa các ngày bằng “không”. Khi đó, theo phương trình (H.25d):
/K, với giả định là thành phần phương sai giữa các ngày bằng “không”. Khi đó, theo phương trình (H.25d):
![]() (H.26a)
(H.26a)
Là ước lượng của ![]() có va = J – 1 = 9 bậc tự do.
có va = J – 1 = 9 bậc tự do.
Ước lượng thứ hai của ![]() , ký hiệu là
, ký hiệu là ![]() , là ước lượng tích lũy của phương sai thu được từ J = 10 giá trị riêng lẻ của s2(
, là ước lượng tích lũy của phương sai thu được từ J = 10 giá trị riêng lẻ của s2(![]() ) bằng cách sử dụng phương trình trong chú thích ở H.3.6, trong đó mười giá trị riêng lẻ được tính từ phương trình (H.25c). Vì bậc tự do của mỗi giá trị này là vi = K – 1 nên công thức thu được cho
) bằng cách sử dụng phương trình trong chú thích ở H.3.6, trong đó mười giá trị riêng lẻ được tính từ phương trình (H.25c). Vì bậc tự do của mỗi giá trị này là vi = K – 1 nên công thức thu được cho ![]() đơn giản là trung bình của chúng. Do đó:
đơn giản là trung bình của chúng. Do đó:
![]() (H.26b)
(H.26b)
Là ước lượng của ![]() có vb = J(K – 1) = 40 bậc tự do.
có vb = J(K – 1) = 40 bậc tự do.
Ước lượng của ![]() được cho bởi phương trình (H.26a) và (H.26b) tương ứng là
được cho bởi phương trình (H.26a) và (H.26b) tương ứng là ![]() và
và ![]() (xem Bảng H.9). Vì ước lượng
(xem Bảng H.9). Vì ước lượng ![]() dựa trên độ biến thiên của các trung bình theo ngày trong khi ước lượng
dựa trên độ biến thiên của các trung bình theo ngày trong khi ước lượng ![]() dựa trên độ biến thiên của các quan trắc hàng ngày, sự khác nhau của chúng cho thấy có thể có sự có mặt của ảnh hưởng do thay đổi từ ngày này sang ngày khác nhưng vẫn duy trì tính không thay đổi tương đối khi thực hiện quan trắc vào một ngày bất kỳ. Sử dụng phép kiểm nghiệm F để kiểm tra khả năng này, do đó giả định thành phần của phương sai giữa các ngày bằng “không”.
dựa trên độ biến thiên của các quan trắc hàng ngày, sự khác nhau của chúng cho thấy có thể có sự có mặt của ảnh hưởng do thay đổi từ ngày này sang ngày khác nhưng vẫn duy trì tính không thay đổi tương đối khi thực hiện quan trắc vào một ngày bất kỳ. Sử dụng phép kiểm nghiệm F để kiểm tra khả năng này, do đó giả định thành phần của phương sai giữa các ngày bằng “không”.
H.5.2.3. Phân bố F là phân bố xác suất là tỉ số ![]() của hai ước lượng độc lập,
của hai ước lượng độc lập, ![]() và
và ![]() , của phương sai s2 của biến ngẫu nhiên phân bố chuẩn [15]. Các tham số va và vb là bậc tự do tương ứng của hai ước lượng và 0 £ F(va,vb) <¥. Giá trị của F được lập thành bảng đối với các giá trị khác nhau của va, vb và các điểm phân vị khác nhau của phân bố F. Giá trị của F(va,vb) > F0,95 hoặc F(va,vb) > F0,975 (giá trị tới hạn) thường được hiểu như là một chỉ báo cho thấy
, của phương sai s2 của biến ngẫu nhiên phân bố chuẩn [15]. Các tham số va và vb là bậc tự do tương ứng của hai ước lượng và 0 £ F(va,vb) <¥. Giá trị của F được lập thành bảng đối với các giá trị khác nhau của va, vb và các điểm phân vị khác nhau của phân bố F. Giá trị của F(va,vb) > F0,95 hoặc F(va,vb) > F0,975 (giá trị tới hạn) thường được hiểu như là một chỉ báo cho thấy ![]() lớn hơn
lớn hơn ![]() một lượng có ý nghĩa thống kê; và xác suất của giá trị F lớn bằng quan trắc được, nếu hai ước lượng đó là ước lượng của cùng một phương sai, tương ứng sẽ nhỏ hơn 0,05 hoặc 0,025 (cũng có thể chọn các giá trị tới hạn khác, ví dụ F0,99).
một lượng có ý nghĩa thống kê; và xác suất của giá trị F lớn bằng quan trắc được, nếu hai ước lượng đó là ước lượng của cùng một phương sai, tương ứng sẽ nhỏ hơn 0,05 hoặc 0,025 (cũng có thể chọn các giá trị tới hạn khác, ví dụ F0,99).
Bảng H.9 – Tổng hợp dữ liệu hiệu chuẩn chuẩn điện thế thu được trong J = 10 ngày, với mỗi trung bình hàng ngày ![]() và độ lệch chuẩn thực nghiệm s2(
và độ lệch chuẩn thực nghiệm s2(![]() k) dựa trên K = 5 quan trắc lặp lại độc lập
k) dựa trên K = 5 quan trắc lặp lại độc lập
|
Đại lượng |
Ngày, j |
|||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
10,000 172 |
10,000 116 |
10,000 013 |
10,000 144 |
10,000 106 |
10,000 031 |
10,000 060 |
10,000 125 |
10,000 163 |
10,000 041 |
|
s(Vjk)/mV |
60 |
77 |
111 |
101 |
67 |
93 |
80 |
73 |
88 |
86 |
|
|
|
|
||||||||
H.5.2.4. Việc áp dụng phép kiểm tra F vào vị trí bằng số đang xét dẫn tới:
![]() (H.27)
(H.27)
Với va = J – 1 = 9 bậc tự do trong tử số và vb = J(K – 1) = 40 bậc tự do trong mẫu số. Do F0,95(9,40) = 2,12 và F0,975(9,40) = 2,45 nên kết luận rằng có sự ảnh hưởng đáng kể về mặt thống kê giữa các ngày có mức ý nghĩa 5% nhưng không có ở mức ý nghĩa 2,5%.
H.5.2.5. Nếu sự tồn tại của ảnh hưởng giữa các ngày bị loại bỏ vì không xem sự khác nhau giữa ![]() và
và ![]() là có ý nghĩa thống kê (một quyết định không thận trọng vì có thể dẫn đến đánh giá thấp độ không đảm bảo) thì phương sai ước lượng
là có ý nghĩa thống kê (một quyết định không thận trọng vì có thể dẫn đến đánh giá thấp độ không đảm bảo) thì phương sai ước lượng ![]() ) và
) và ![]() cần được tính theo phương trình (H.24b). Mối quan hệ đó tương đương với việc gộp các ước lượng
cần được tính theo phương trình (H.24b). Mối quan hệ đó tương đương với việc gộp các ước lượng ![]() và
và ![]() (nghĩa là, lấy trung bình có trọng số của
(nghĩa là, lấy trung bình có trọng số của ![]() và
và ![]() , từng số được lấy trọng số bằng bậc tự do riêng của nó va và vb – xem H.3.6, chú thích) để thu được ước lượng phương sai tốt nhất của các quan trắc; chia ước lượng đó cho JK, số quan trắc, để thu được ước lượng phương sai tốt nhất
, từng số được lấy trọng số bằng bậc tự do riêng của nó va và vb – xem H.3.6, chú thích) để thu được ước lượng phương sai tốt nhất của các quan trắc; chia ước lượng đó cho JK, số quan trắc, để thu được ước lượng phương sai tốt nhất ![]() ) của trung bình các quan trắc. Theo quy trình này thu được:
) của trung bình các quan trắc. Theo quy trình này thu được:
![]() (H.28a)
(H.28a)
![]() hoặc
hoặc ![]() (H.28b)
(H.28b)
Với ![]() có JK – 1 = 49 bậc tự do.
có JK – 1 = 49 bậc tự do.
Nếu giả định rằng đã tính đến tất cả sự hiệu chính đối với ảnh hưởng hệ thống và tất cả các thành phần khác của độ không đảm bảo là không đáng kể thì kết quả phép hiệu chuẩn có thể được diễn tả là VS = ![]() = 10,000 097 V (xem Bảng H.9) với độ không đảm bảo chuẩn tổng hợp
= 10,000 097 V (xem Bảng H.9) với độ không đảm bảo chuẩn tổng hợp ![]() = uc = 13mV và với uc có bậc tự do là 49.
= uc = 13mV và với uc có bậc tự do là 49.
CHÚ THÍCH 1: Trong thực tế, rất có khả năng các thành phần của độ không đảm bảo có ý nghĩa và do đó phải tổng hợp các thành phần độ không đảm bảo thống kê thu được từ các quan trắc (xem H.5.1, Chú thích).
CHÚ THÍCH 2: Phương trình (H.28a) cho ![]() có thể được chỉ là bằng phương trình (H.24b) bằng cách viết tổng kép, được ký hiệu là S, trong phương trình đó như sau:
có thể được chỉ là bằng phương trình (H.24b) bằng cách viết tổng kép, được ký hiệu là S, trong phương trình đó như sau:
![]()
H.5.2.6. Nếu sự có mặt của ảnh hưởng giữa các ngày là chấp nhận được (một quyết định khôn ngoan vì nó tránh được việc đánh giá thấp độ không đảm bảo) và được giả định là ngẫu nhiên, khi đó phương sai ![]() được tính từ J = 10 trung bình theo ngày theo phương trình (H.25d) ước lượng không phải
được tính từ J = 10 trung bình theo ngày theo phương trình (H.25d) ước lượng không phải ![]() /k như đặt ra trong H.5.2.2 mà là
/k như đặt ra trong H.5.2.2 mà là ![]() /k +
/k + ![]() , trong đó
, trong đó ![]() là thành phần phương sai ngẫu nhiên giữa các ngày. Điều này nghĩa là:
là thành phần phương sai ngẫu nhiên giữa các ngày. Điều này nghĩa là:
![]() =
= ![]() /K +
/K + ![]() (H.29)
(H.29)
Trong đó ![]() ước lượng
ước lượng ![]() và
và ![]() ước lượng
ước lượng ![]() . Do
. Do ![]() được tính từ phương trình (H.26b) chỉ phụ thuộc vào độ biến động trong ngày của quan trắc, nên có thể lấy
được tính từ phương trình (H.26b) chỉ phụ thuộc vào độ biến động trong ngày của quan trắc, nên có thể lấy ![]() =
= ![]() . Do đó, tỉ số
. Do đó, tỉ số ![]() được sử dụng cho phép kiểm nghiệm F trong H.5.2.4 trở thành:
được sử dụng cho phép kiểm nghiệm F trong H.5.2.4 trở thành:
![]() (H.30)
(H.30)
Khi đó dẫn tới:
![]() (H.31a)
(H.31a)
![]() = (43 mV)2, hoặc sB = 43 mV
= (43 mV)2, hoặc sB = 43 mV
![]() =
= ![]() =(85 mV)2, hoặc sw = 85 mV (H.31b)
=(85 mV)2, hoặc sw = 85 mV (H.31b)
Phương sai ước lượng của ![]() thu được từ
thu được từ ![]() , phương trình (H.25d), vì
, phương trình (H.25d), vì ![]() phản ánh đúng thành phần ngẫu nhiên của phương sai trong ngày và phương sai giữa các ngày [xem phương trình (H.29)]. Do đó:
phản ánh đúng thành phần ngẫu nhiên của phương sai trong ngày và phương sai giữa các ngày [xem phương trình (H.29)]. Do đó:
![]() (H.32)
(H.32)
= (57 mV)2/10, hoặc ![]()
Với![]() có bậc tự do J – 1 = 9.
có bậc tự do J – 1 = 9.
Bậc tự do của ![]() (và do đó sw) là J(K – 1) = 40 [xem phương trình (H.26b)]. Bậc tự do của
(và do đó sw) là J(K – 1) = 40 [xem phương trình (H.26b)]. Bậc tự do của ![]() (và do đó sB) là bậc tự do hiệu dụng của hiệu
(và do đó sB) là bậc tự do hiệu dụng của hiệu ![]() =
= ![]() –
– ![]() /K [phương trình (H.31a)] nhưng ước lượng của nó là khó hiểu.
/K [phương trình (H.31a)] nhưng ước lượng của nó là khó hiểu.
H.5.2.7. Ước lượng tốt nhất của hiệu điện thế của chuẩn điện thế khi đó là Vs =![]() = 10,000 097 V với s(
= 10,000 097 V với s(![]() ) = uc = 18 mV như được cho trong phương trình (H.32). Giá trị này của uc và bậc tự do 9 của nó được so sánh với uc = 13 mV và bậc tự do 49, kết quả thu được trong H.5.2.5 [phương trình (H.28b)] khi loại bỏ sự có mặt của ảnh hưởng giữa các ngày.
) = uc = 18 mV như được cho trong phương trình (H.32). Giá trị này của uc và bậc tự do 9 của nó được so sánh với uc = 13 mV và bậc tự do 49, kết quả thu được trong H.5.2.5 [phương trình (H.28b)] khi loại bỏ sự có mặt của ảnh hưởng giữa các ngày.
Trong phép đo thực tế ảnh hưởng giữa các ngày rõ ràng cần được nghiên cứu thêm, nếu có thể, để xác định nguyên nhân của nó và có mặt ảnh hưởng hệ thống làm vô hiệu hóa việc sử dụng phương pháp ANOVA hay không. Như đã chỉ ra ở phần đầu của ví dụ này, kỹ thuật ANOVA được thiết kế để xác định và đánh giá các thành phần của độ không đảm bảo sinh ra từ ảnh hưởng ngẫu nhiên; chúng không thể cung cấp thông tin về thành phần sinh ra từ ảnh hưởng hệ thống.
H.5.3. Vai trò của ANOVA trong phép đo
H.5.3.1. Ví dụ về chuẩn điện thế này minh họa điều thường được gọi là thiết kế lồng nhau một giai đoạn cân bằng. Nó là thiết kế lồng nhau giai đoạn một vì có một mức “lồng” của các quan trắc với một thừa số, ngày thực hiện quan trắc, bị làm thay đổi trong phép đo. Nó cân bằng vì cùng số lượng quan trắc được thực hiện mỗi ngày. Sự phân tích được trình bày trong ví dụ có thể được sử dụng để xác định xem có “ảnh hưởng của người vận hành”, “ảnh hưởng của phương tiện đo”, “ảnh hưởng của phòng thí nghiệm”, “ảnh hưởng của mẫu” hay thậm chí “ảnh hưởng của phương pháp” trong một phép đo cụ thể không. Do đó trong ví dụ này, có thể tưởng tượng thay các quan trắc được thực hiện vào J ngày khác nhau bằng các quan trắc được thực hiện vào cùng một ngày nhưng bởi J người vận hành khác nhau; thành phần của phương sai giữa các ngày khi đó trở thành thành phần của phương sai gắn với những người vận hành khác nhau.
H.5.3.2. Như chú thích trong H.5, phương pháp ANOVA được sử dụng rộng rãi trong việc chứng nhận mẫu chuẩn (RM) bằng thử nghiệm liên phòng. Việc chứng nhận như vậy thường gồm có một số phòng thí nghiệm độc lập, thành thạo ngang nhau đo mẫu vật liệu về tính chất mà vật liệu được chứng nhận. Thường giả định rằng sự khác nhau giữa các kết quả riêng lẻ, trong và giữa các phòng thí nghiệm, về bản chất là có tính thống kê bất kể do nguyên nhân nào. Mỗi trung bình của phòng thí nghiệm được coi là một ước lượng không chệch về tính chất của vật liệu và trung bình không lấy trọng số của các trung bình phòng thí nghiệm thường được giả định là ước lượng tốt nhất của tính chất đó.
Việc chứng nhận RM có thể gồm I phòng thí nghiệm khác nhau, mỗi phòng đo tính chất yêu cầu của J mẫu vật liệu khác nhau, với mỗi phép đo của một mẫu có K quan trắc lặp lại độc lập. Do đó tổng số quan trắc là IJK và tổng số mẫu là IJ. Đây là ví dụ về thiết kế lồng nhau cân bằng, hai giai đoạn tương tự với ví dụ chuẩn điện thế một giai đoạn ở trên. Trong trường hợp này, có hai mức “lồng” các quan trắc với hai thừa số khác nhau, mẫu và phòng thí nghiệm, được thay đổi trong phép đo. Thiết kế là cân bằng vì mỗi mẫu được quan trắc với số lần giống nhau (K) trong từng phòng thí nghiệm và từng phòng thí nghiệm đo số lượng mẫu giống nhau (J). Tương tự như ví dụ chuẩn điện áp, trong trường hợp RM mục đích của phân tích dữ liệu là khảo sát khả năng có thể có ảnh hưởng giữa các mẫu, ảnh hưởng giữa các phòng thí nghiệm và xác định độ không đảm bảo thích hợp để ấn định ước lượng tốt nhất cho giá trị của tính chất được chứng nhận. Để phù hợp với nội dung trên, ước lượng được giả định là trung bình của I trung bình của phòng thí nghiệm, cũng là trung bình của IJK quan trắc.
H.5.3.3. Mục 3.4.2 trình bày tầm quan trọng của việc thay đổi đại lượng đầu vào mà kết quả đo phụ thuộc sao cho độ không đảm bảo dựa trên dữ liệu quan trắc được đánh giá thống kê. Thiết kế lồng nhau và sự phân tích dữ liệu thu được bằng phương pháp ANOVA có thể được sử dụng thành công trong nhiều tình huống đo gặp trong thực tế.
Tuy nhiên, như đã trình bày trong 3.4.1, hiếm khi có thể thực hiện việc thay đổi tất cả đại lượng đầu vào do giới hạn về thời gian và nguồn lực; tốt nhất, trong hầu hết tình huống đo thực tế, chỉ có thể đánh giá một vài thành phần của độ không đảm bảo bằng cách sử dụng phương pháp ANOVA. Như đã trình bày trong 4.3.1, nhiều thành phần phải được đánh giá bằng sự xét đoán khoa học sử dụng tất cả thông tin có sẵn về độ biến thiên có thể có của đại lượng đầu vào đang nói đến; trong nhiều trường hợp một thành phần độ không đảm bảo, như sinh ra từ ảnh hưởng giữa các mẫu, ảnh hưởng giữa các phòng thí nghiệm, ảnh hưởng giữa các phương tiện hay ảnh hưởng giữa những người vận hành không thể được đánh giá bằng phân tích thống kê các dãy quan trắc nhưng phải được đánh giá từ tổ hợp thông tin có sẵn.
H.6. Phép đo trên thang đo quy chiếu: độ cứng
Độ cứng là ví dụ về khái niệm vật lý không thể định lượng mà không viện dẫn tới một phương pháp đo; nó không có đơn vị độc lập của phương pháp như vậy. Đại lượng “độ cứng” không giống các đại lượng có thể đo được cổ điển ở chỗ không thể đưa nó vào các phương trình đại số để xác định các đại lượng có thể đo được khác (mặc dù đôi khi nó được sử dụng trong các phương trình thực nghiệm liên hệ độ cứng tới tính chất khác của một loại vật liệu). Độ lớn của nó được xác định bằng phép đo quy ước, của một kích thước thẳng của vết lõm trong khối vật liệu được quan tâm hoặc tấm mẫu. Phép đo được thực hiện theo một văn bản tiêu chuẩn, gồm có sự mô tả “mũi thử”, cấu trúc của máy mà nhờ đó mũi thử được sử dụng và cách vận hành máy. Có nhiều tiêu chuẩn được biên soạn nên có nhiều thang đo độ cứng.
H.6.1. Vấn đề của phép đo
Trong ví dụ này, độ cứng của tấm mẫu vật liệu được xác định theo thang đo “Rockwell C” sử dụng máy đã được hiệu chuẩn theo máy chuẩn quốc gia. Đơn vị thang độ cứng Rockwell-C là 0,002 mm với độ cứng mà trên đó thang đo được xác định là 100 x (0,002 mm) trừ trung bình độ sâu, đo bằng mm, của năm vết lõm. Giá trị của đại lượng đó được chia cho đơn vị thang Rockwell 0,002 mm được gọi là “chỉ số độ cứng HRC”. Trong ví dụ này, đại lượng được gọi đơn giản là “độ cứng”, ký hiệu là hRockwell C và trị số của độ cứng được thể hiện theo đơn vị độ dài Rockwell được gọi là “chỉ số độ cứng”, HRockwell C.
H.6.2. Mô hình toán
Để tính trung bình độ sâu các vết lõm được tạo ra trong tấm mẫu bằng máy được sử dụng để xác định độ cứng, hoặc máy hiệu chuẩn, phải bổ sung sự hiệu chính để xác định trung bình của độ sâu các vết lõm đã được tạo ra trong cùng một tấm mẫu bằng máy chuẩn quốc gia. Do đó:
![]() (H.33a)
(H.33a)
![]() (H.33b)
(H.33b)
Trong đó:
![]() là trung bình độ sâu của năm vết lõm do máy hiệu chuẩn tạo ra trên cùng một tấm mẫu;
là trung bình độ sâu của năm vết lõm do máy hiệu chuẩn tạo ra trên cùng một tấm mẫu;
![]() là sự hiệu chính thu được từ sự so sánh máy hiệu chuẩn với máy chuẩn quốc gia bằng cách sử dụng tấm chuẩn sao truyền, bằng trung bình độ sâu của 5m vết lõm do máy chuẩn quốc gia tạo ra trong mẫu này trừ trung bình độ sâu của 5n vết lõm do máy hiệu chuẩn tạo ra trong cùng một tấm mẫu;
là sự hiệu chính thu được từ sự so sánh máy hiệu chuẩn với máy chuẩn quốc gia bằng cách sử dụng tấm chuẩn sao truyền, bằng trung bình độ sâu của 5m vết lõm do máy chuẩn quốc gia tạo ra trong mẫu này trừ trung bình độ sâu của 5n vết lõm do máy hiệu chuẩn tạo ra trong cùng một tấm mẫu;
![]() là chênh lệch về độ cứng (được thể hiện như sự khác nhau của trung bình độ sâu của vết lõm) giữa hai phần của tấm chuẩn sao truyền tương ứng được hai máy sử dụng cho các vết lõm, giả định bằng “không”; và
là chênh lệch về độ cứng (được thể hiện như sự khác nhau của trung bình độ sâu của vết lõm) giữa hai phần của tấm chuẩn sao truyền tương ứng được hai máy sử dụng cho các vết lõm, giả định bằng “không”; và
![]() là sai số do thiếu sót về độ lặp lại của máy chuẩn quốc gia và sự định nghĩa không đầy đủ về đại lượng độ cứng. Mặc dù
là sai số do thiếu sót về độ lặp lại của máy chuẩn quốc gia và sự định nghĩa không đầy đủ về đại lượng độ cứng. Mặc dù ![]() phải được giả định bằng “không” nhưng nó vẫn có độ không đảm bảo chuẩn là u(
phải được giả định bằng “không” nhưng nó vẫn có độ không đảm bảo chuẩn là u(![]() ).
).
Do tất cả đạo hàm riêng, ![]() của hàm phương trình (H.33a) đều bằng -1 nên độ không đảm bảo chuẩn tổng hợp uc(h) của độ cứng tấm mẫu khi đó bằng máy hiệu chuẩn được cho đơn giản bằng:
của hàm phương trình (H.33a) đều bằng -1 nên độ không đảm bảo chuẩn tổng hợp uc(h) của độ cứng tấm mẫu khi đó bằng máy hiệu chuẩn được cho đơn giản bằng:
![]() (H.34)
(H.34)
Trong đó để đơn giản ký hiệu h ≡ hRockwell C.
H.6.3. Các phương sai đóng góp vào độ không đảm bảo
H.6.3.1. Độ không đảm bảo của độ sâu trung bình vết lõm![]() của tấm mẫu, u(
của tấm mẫu, u(![]() )
)
Độ không đảm bảo của quan trắc lặp lại. Lặp lại nghiêm ngặt của quan trắc là không thể vì không thể tạo ra vết lõm mới ở vị trí của vết lõm trước. Do mỗi vết lõm phải được tạo ra ở một vị trí khác nên mọi biến động trong kết quả bao gồm cả ảnh hưởng của biến động về độ cứng giữa các vị trí khác nhau. Do đó, u(![]() ), độ không đảm bảo chuẩn của trung bình độ sâu của năm vết lõm trong tấm mẫu do máy hiệu chuẩn, được lấy là sp(dk)/
), độ không đảm bảo chuẩn của trung bình độ sâu của năm vết lõm trong tấm mẫu do máy hiệu chuẩn, được lấy là sp(dk)/![]() , trong đó sp(dk) là độ lệch chuẩn thực nghiệm tích lũy của độ sâu các vết lõm được xác định bằng phép đo “lặp lại” trên tấm đã biết là có độ cứng rất đồng đều (xem 4.2.4).
, trong đó sp(dk) là độ lệch chuẩn thực nghiệm tích lũy của độ sâu các vết lõm được xác định bằng phép đo “lặp lại” trên tấm đã biết là có độ cứng rất đồng đều (xem 4.2.4).
Độ không đảm bảo của số chỉ. Mặc dù sự hiệu chính cho ![]() do sự hiển thị của máy hiệu chuẩn là bằng “không” nhưng vẫn có một độ không đảm bảo trong
do sự hiển thị của máy hiệu chuẩn là bằng “không” nhưng vẫn có một độ không đảm bảo trong ![]() do độ không đảm bảo của số chỉ vết lõm do độ phân giải d của sự hiển thị được cho bằng u2(d) = d2/12 (xem F.2.2.1). Do đó, phương sai ước lượng của
do độ không đảm bảo của số chỉ vết lõm do độ phân giải d của sự hiển thị được cho bằng u2(d) = d2/12 (xem F.2.2.1). Do đó, phương sai ước lượng của ![]() là:
là:
u2(![]() ) = s2(dk)/5 + d2/12 (H.35)
) = s2(dk)/5 + d2/12 (H.35)
H.6.3.2. Độ không đảm bảo của sự hiệu chính đối với sự khác nhau giữa hai máy, uDc
Như đã trình bày trong H.6.2, Dc là sự hiệu chính đối với sự khác nhau giữa máy chuẩn quốc gia và máy hiệu chuẩn. Sự hiệu chính này có thể được thể hiện là Dc = z’S – z’, trong đó ![]() là độ sâu trung bình của 5m vết lõm do máy chuẩn quốc gia tạo ra trong chuẩn sao truyền; và
là độ sâu trung bình của 5m vết lõm do máy chuẩn quốc gia tạo ra trong chuẩn sao truyền; và ![]() là độ sâu trung bình của 5n vết lõm do máy hiệu chuẩn tạo ra trong cùng tấm mẫu. Do giả định đối với sự so sánh độ không đảm bảo do độ phân giải hiển thị của từng máy gây ra là không đáng kể, phương sai ước lượng của Dc là:
là độ sâu trung bình của 5n vết lõm do máy hiệu chuẩn tạo ra trong cùng tấm mẫu. Do giả định đối với sự so sánh độ không đảm bảo do độ phân giải hiển thị của từng máy gây ra là không đáng kể, phương sai ước lượng của Dc là:
![]() (H.36)
(H.36)
Trong đó:
![]() là trung bình của các phương sai thực nghiệm của trung bình của từng vết lõm trong m loạt vết lõm zS,ik do máy chuẩn tạo ra;
là trung bình của các phương sai thực nghiệm của trung bình của từng vết lõm trong m loạt vết lõm zS,ik do máy chuẩn tạo ra;
![]() là trung bình của các phương sai thực nghiệm của trung bình của từng vết lõm trong n loạt vết lõm zik do máy chuẩn tạo ra.
là trung bình của các phương sai thực nghiệm của trung bình của từng vết lõm trong n loạt vết lõm zik do máy chuẩn tạo ra.
CHÚ THÍCH: Phương sai ![]() và
và ![]() là ước lượng tích lũy của phương sai – xem phần thảo luận của phương trình (H.26b) trong H.5.2.2.
là ước lượng tích lũy của phương sai – xem phần thảo luận của phương trình (H.26b) trong H.5.2.2.
H.6.3.3. Độ không đảm bảo của sự hiệu chính do biến động độ cứng của tấm chuẩn sao truyền, u(Db)
Khuyến nghị quốc tế OIML R 12, Kiểm định và hiệu chuẩn tấm độ cứng Rockwell C tiêu chuẩn hóa, yêu cầu độ sâu lớn nhất và nhỏ nhất của vết lõm thu được từ năm phép thử trên tấm chuẩn sao truyền không được chênh lệch quá một phần nhỏ x của độ sâu trung bình của vết lõm, trong đó x là hàm số của mức độ cứng. Do đó, đặt chênh lệch lớn nhất về độ sâu của vết lõm trên toàn bộ tấm là xz’, trong đó z’ được xác định như trong H.6.3.2 với n = 5. Cũng đặt chênh lệch lớn nhất được mô tả bằng phân bố xác suất tam giác quanh giá trị trung bình xz’/2 (tương tự giả thiết rằng các giá trị gần giá trị trung tâm có khả năng xuất hiện nhiều hơn các giá trị cực trị – xem 4.3.9). Khi đó, nếu phương trình (9b) trong 4.3.9 a = xz’/2, thì phương sai ước lượng của sự hiệu chính độ sâu trung bình của vết lõm do chênh lệch độ cứng thể hiện tương ứng cho máy chuẩn và máy hiệu chuẩn tạo ra là:
![]() (H.37)
(H.37)
Như đã trình bày trong H.6.2, giả định ước lượng tốt nhất của sự hiệu chính ![]() bằng “không”.
bằng “không”.
H.6.3.4. Độ không đảm bảo của máy chuẩn quốc gia và định nghĩa độ cứng, u(DS)
Độ không đảm bảo của máy chuẩn quốc gia cùng với độ không đảm bảo do định nghĩa không đầy đủ về đại lượng độ cứng được công bố là độ lệch chuẩn ước lượng u(DS) (đại lượng có thứ nguyên độ dài).
H.6.4. Độ không đảm bảo chuẩn tổng hợp, uc(h)
Tập hợp của các số hạng riêng lẻ được thảo luận trong H.6.3.1 đến H.6.3.4 và thay vào phương trình (H.34) mang lại phương sai ước lượng của phép đo độ cứng
![]() (H.38)
(H.38)
Và độ không đảm bảo chuẩn tổng hợp là uc(h).
H.6.5. Ví dụ bằng số
Bảng H.10 tổng hợp dữ liệu cho ví dụ này.
Bảng H.10 – Tổng hợp dữ liệu đối với việc xác định độ cứng của tấm mẫu trên thang đo Rockwell C
|
Nguồn độ không đảm bảo |
Giá trị |
|
Độ sâu trung bình |
36,0 đơn vị thang đo Rockwell |
|
Chỉ số độ cứng được chỉ thị của tấm mẫu từ 5 vết lõm: HRockwell C = hRockwell C/(0,002 mm) = [100(0,002 mm) – 0,072]/(0,002 mm) (Xem H.6.1) |
64,0 HRC |
|
Độ lệch chuẩn thực nghiệm tích lũy sp=(dk) của độ sâu vết lõm do máy hiệu chuẩn tạo ra trên tấm mẫu có độ cứng đồng đều. |
0,45 đơn vị thang đo Rockwell |
|
Độ phân giải d hiển thị của máy hiệu chuẩn. |
0,1 đơn vị thang đo Rockwell |
|
sav( |
0,10 đơn vị thang đo Rockwell, m =6 |
|
sav( |
0,11 đơn vị thang đo Rockwell, n =6 |
|
Phần biến đổi cho phép x của độ sâu xâm nhập vào tấm chuẩn sao truyền |
1,5 x 10-2 |
|
Độ không đảm bảo chuẩn u(DS) của máy chuẩn quốc gia và định nghĩa độ cứng |
0,5 đơn vị thang đo Rockwell |
Thang đo là Rockwell C, viết tắt là HRC. Đơn vị của thang đo Rockwell bằng 0,002 mm và do đó, trong Bảng H.10 và sau này, nó được hiểu là (ví dụ) “36,0 đơn vị thang Rockwell” có nghĩa là 36,0 x (0,002 mm) = 0,072 mm và đơn giản là cách thuận tiện để thể hiện dữ liệu và kết quả.
Nếu giá trị đối với đại lượng liên quan được cho trong Bảng H.10 được thay vào phương trình (H.38) sẽ thu được hai biểu thức sau:
![]() (đơn vị thang đo Rockwell)2
(đơn vị thang đo Rockwell)2
= 0,307 (đơn vị thang đo Rockwell)2
uc(h) = 0,55 đơn vị thang đo Rockwell = 0,001 1 mm
trong đó đối với mục đích tính độ không đảm bảo, lấy z’ = ![]() = 36,0 đơn vị thang đo Rockwell là thích hợp.
= 36,0 đơn vị thang đo Rockwell là thích hợp.
Do đó, nếu giả định rằng Dc = 0 thì độ cứng của tấm mẫu là:
hRockwell C = 64,0 đơn vị thang đo Rockwell hoặc 0,128 0 mm với độ không đảm bảo chuẩn tổng hợp uc = 0,55 đơn vị thang đo Rockwell hoặc 0,001 1 mm.
Chỉ số độ cứng của tấm là hRockwell C/(0,002 mm) = (0,128 0 mm) / (0,002 mm) hoặc
HRockwell C = 64,0 HRC với độ không đảm bảo chuẩn tổng hợp uc = 0,55 HRC.
Bổ sung cho thành phần của độ không đảm bảo do máy chuẩn quốc gia và định nghĩa của độ cứng, u(DS) = 0,5 đơn vị thang đo Rockwell, các thành phần có ý nghĩa của độ không đảm bảo là thành phần lặp lại của máy, sp(dk)/![]() = 0,20 đơn vị thang đo Rockwell; và sự thay đổi độ cứng của tấm chuẩn sao truyền, bằng (xz’)2/24 = 0,11 đơn vị thang đo Rockwell. Bậc tự do hiệu dụng của uc có thể được đánh giá bằng cách sử dụng công thức Welch-Satterthwaite theo cách được minh họa trong H.1.6.
= 0,20 đơn vị thang đo Rockwell; và sự thay đổi độ cứng của tấm chuẩn sao truyền, bằng (xz’)2/24 = 0,11 đơn vị thang đo Rockwell. Bậc tự do hiệu dụng của uc có thể được đánh giá bằng cách sử dụng công thức Welch-Satterthwaite theo cách được minh họa trong H.1.6.
PHỤ LỤC J
(tham khảo)
BẢNG CHÚ GIẢI CÁC KÝ HIỆU QUAN TRỌNG
|
a |
nửa độ rộng của phân bố chữ nhật các giá trị có thể có của đại lượng đầu vào Xi: a = (a+ – a–)/2 |
|
a+ |
giá trị biên trên của đại lượng đầu vào Xi |
|
a– |
giá trị biên dưới của đại lượng đầu vào Xi |
|
b+ |
giá trị biên trên của độ lệch của đại lượng đầu vào Xi so với ước lượng xi: b+ = a+ – xi |
|
b– |
giá trị biên dưới của độ lệch của đại lượng đầu vào Xi so với ước lượng xi: b– = xi – a– |
|
ci |
đạo hàm riêng hay hệ số độ nhạy
|
|
f |
mối quan hệ hàm số giữa đại lượng đo Y và đại lượng đầu vào Xi mà Y phụ thuộc, và giữa ước lượng đầu ra y và ước lượng đầu vào xi mà y phụ thuộc. |
|
|
đạo hàm riêng theo đại lượng đầu vào Xi của mối quan hệ hàm số f giữa đại lượng đo Y và đại lượng đầu vào Xi mà Y phụ thuộc, được đánh giá bằng ước lượng xi cho Xi |
|
k |
hệ số phủ được sử dụng để tính độ không đảm bảo mở rộng U = kuc(y) của ước lượng đầu ra y từ độ không đảm bảo chuẩn tổng hợp uc(y), trong đó U xác định khoảng Y = y ± U có mức tin cậy cao. |
|
kp |
hệ số phủ được sử dụng để tính độ không đảm bảo mở rộng Up = kpuc(y) của ước lượng đầu ra y từ độ không đảm bảo chuẩn tổng hợp uc(y), trong đó Up xác định khoảng Y = y ± Up có mức tin cậy cao, xác định p |
|
n |
số quan trắc lặp lại |
|
N |
số đại lượng đầu vào Xi mà đại lượng đo Y phụ thuộc |
|
p |
xác suất; mức tin cậy: 0 £ p £ 1 |
|
q |
đại lượng thay đổi ngẫu nhiên được mô tả bằng phân bố xác suất |
|
|
trung bình cộng hoặc trung bình của n quan trắc lặp lại độc lập qk của đại lượng thay đổi ngẫu nhiên q |
|
ước lượng của kỳ vọng hoặc trung bình mq của phân bố xác suất của q |
|
|
qk |
quan trắc lặp lại độc lập thứ k của đại lượng thay đổi ngẫu nhiên q |
|
r(xi,xj) |
hệ số tương quan ước lượng gắn với các ước lượng đầu vào xi và xj ước lượng đại lượng đầu vào Xi và Xj: r(xi,xj) = u(xi,xj)/[u(xi)u(xj)] |
|
|
hệ số tương quan ước lượng của trung bình đầu vào
|
|
r(yi,yj) |
hệ số tương quan ước lượng gắn với các ước lượng đầu ra yi và yj khi hai hay nhiều đại lượng đo hoặc đại lượng đầu ra được xác định trong cùng một phép đo |
|
|
ước lượng tổng hợp hoặc gộp của phương sai |
|
sp |
độ lệch chuẩn thực nghiệm gộp, bằng dương căn bậc hai của |
|
|
phương sai thực nghiệm của trung bình |
|
ước lượng của phương sai s2/n của |
|
|
phương sai ước lượng thu được từ đánh giá loại A |
|
|
|
độ lệch chuẩn thực nghiệm của trung bình |
|
hàm ước lượng chệch của s( |
|
|
độ không đảm bảo chuẩn thu được từ đánh giá Loại A |
|
|
|
phương sai thực nghiệm xác định từ n quan trắc lặp lại độc lập qk của q |
|
ước lượng của phương sai s2 của phân bố xác suất của q |
|
|
s(qk) |
độ lệch chuẩn thực nghiệm, bằng dương căn bậc hai của |
|
hàm ước lượng chệch của độ lệch chuẩn s của phân bố xác suất của q |
|
|
|
phương sai thực nghiệm của trung bình đầu vào |
|
phương sai ước lượng thu được từ đánh giá Loại A |
|
|
|
phương sai thực nghiệm của trung bình đầu vào |
|
độ không đảm bảo chuẩn thu được từ đánh giá Loại A |
|
|
|
ước lượng của hiệp phương sai của trung bình |
|
hiệp phương sai ước lượng thu được từ đánh giá Loại A |
|
|
|
ước lượng của hiệp phương sai của trung bình đầu vào |
|
hiệp phương sai ước lượng thu được từ đánh giá Loại A |
|
|
tp(v) |
hệ số t từ phân bố t đối với v bậc tự do ứng với xác suất p đã cho |
|
tp(veff) |
hệ số t từ phân bố t đối với veff bậc tự do ứng với xác suất p đã cho, được sử dụng để tính độ không đảm bảo mở rộng Up |
|
u2(xi) |
phương sai ước lượng gắn với ước lượng đầu vào xi ước lượng đại lượng đầu vào Xi CHÚ THÍCH: Khi xi được xác định từ trung bình cộng hoặc trung bình của n quan trắc lặp lại độc lập, u2(xi) = s2( |
|
u(xi) |
Độ không đảm bảo chuẩn của ước lượng đầu vào xi ước lượng đại lượng đầu vào Xi, bằng dương căn bậc hai u2(xi) CHÚ THÍCH: Khi xi được xác định từ trung bình cộng hoặc trung bình của n quan trắc lặp lại độc lập, u(xi) = s( |
|
u(xi,xj) |
hiệp phương sai ước lượng gắn với hai ước lượng đầu vào xi và xj ước lượng đại lượng đầu vào Xi và Xj. CHÚ THÍCH; Khi xi và xj được xác định từ n cặp quan trắc lặp lại đồng thời độc lập, u(xi,xj) = |
|
|
phương sai tổng hợp gắn với lượng đầu ra y |
|
uc(y) |
độ không đảm bảo chuẩn tổng hợp của ước lượng đầu ra y, bằng dương căn bậc hai |
|
ucA(y) |
độ không đảm bảo chuẩn tổng hợp của ước lượng đầu ra y được xác định từ độ không đảm bảo chuẩn và hiệp phương sai ước lượng thu được từ riêng đánh giá Loại A. |
|
ucB(y) |
độ không đảm bảo chuẩn tổng hợp của ước lượng đầu ra y được xác định từ độ không đảm bảo chuẩn và hiệp phương sai ước lượng thu được từ riêng đánh giá Loại B. |
|
uc(yi) |
độ không đảm bảo chuẩn tổng hợp của ước lượng đầu ra yi khi có từ hai đại lượng đo hoặc đại lượng đầu ra trở lên được xác định trong cùng một phép đo |
|
|
thành phần của phương sai tổng hợp |
|
ui(y) |
thành phần của độ không đảm bảo chuẩn tổng hợp uc(y) của ước lượng đầu ra y được tạo ra bởi độ không đảm bảo chuẩn của ước lượng đầu vào xi: |
|
u(yi,yj) |
hiệp phương sai ước lượng gắn với ước lượng đầu ra yi và yj được xác định trong cùng một phép đo. |
|
u(xi)/|xi| |
độ không đảm bảo chuẩn tương đối của ước lượng đầu vào xi |
|
uc(y)/|y| |
độ không đảm bảo chuẩn tổng hợp đối với ước lượng đầu ra y |
|
[u(xi)/|xi|]2 |
phương sai tương đối ước lượng gắn với ước lượng đầu vào xi |
|
[uc(y)/y]2 |
phương sai tổng hợp tương đối gắn với ước lượng đầu ra y |
|
|
hiệp phương sai tương đối ước lượng gắn với ước lượng đầu vào xi và xj |
|
U |
độ không đảm bảo mở rộng của ước lượng đầu ra y xác định khoảng Y = y ± U có mức tin cậy cao, bằng hệ số phủ k nhân độ không đảm bảo chuẩn tổng hợp uc(y) của y: U = kuc(y) |
|
Up |
độ không đảm bảo mở rộng của ước lượng đầu ra y xác định khoảng Y = y ± Up có mức tin cậy cao và xác định p, bằng hệ số phủ kp nhân độ không đảm bảo chuẩn tổng hợp uc(y) của Y: Up = kpuc(y) |
|
xi |
ước lượng của đại lượng đầu vào Xi CHÚ THÍCH: Khi xi được xác định từ trung bình cộng hay trung bình của n quan trắc lặp lại độc lập thì xi = |
|
Xi |
đại lượng đầu vào thứ i mà đại lượng đo Y phụ thuộc CHÚ THÍCH: Xi có thể là đại lượng vật lý hoặc biến ngẫu nhiên (xem 4.1.1, Chú thích 1) |
|
|
ước lượng giá trị của đại lượng đầu vào Xi, bằng trung bình cộng hay trung bình của n quan trắc lặp lại độc lập Xi,k của Xi |
|
Xi,k |
quan trắc lặp lại độc lập thứ k của Xi |
|
y |
ước lượng của đại lượng đo Y |
|
kết quả đo |
|
|
ước lượng đầu ra |
|
|
yi |
ước lượng của đại lượng Yi khi có từ hai đại lượng đo trở lên được xác định trong cùng một phép đo |
|
Y |
đại lượng đo |
|
|
độ không đảm bảo tương đối ước lượng của độ không đảm bảo chuẩn u(xi) của ước lượng đầu vào xi |
|
mq |
kỳ vọng hay trung bình của phân bố xác suất của đại lượng thay đổi ngẫu nhiên q |
|
v |
bậc tự do (chung) |
|
vi |
bậc tự do, hay bậc tự do hiệu dụng, của độ không đảm bảo chuẩn u(xi) của ước lượng đầu vào xi |
|
veff |
bậc tự do hiệu dụng của uc(y), được sử dụng để thu được tp(veff) để tính độ không đảm bảo mở rộng Up. |
|
veffA |
bậc tự do hiệu dụng của độ không đảm bảo chuẩn tổng hợp được xác định từ độ không đảm bảo chuẩn thu được từ riêng sự đánh giá Loại A |
|
veffB |
bậc tự do hiệu dụng của độ không đảm bảo chuẩn tổng hợp được xác định từ độ không đảm bảo chuẩn thu được từ riêng sự đánh giá Loại B |
|
s2 |
phương sai của phân bố xác suất của (ví dụ) đại lượng thay đổi ngẫu nhiên q, được ước lượng bằng s2(qk) |
|
s |
độ lệch chuẩn của phân bố xác suất, bằng dương căn bậc hai s2 |
|
s(qk) là hàm ước lượng chệch của s |
|
|
|
phương sai của |
|
|
độ lệch chuẩn của |
|
|
|
|
|
phương sai của độ chệch chuẩn thực nghiệm |
|
|
độ lệch chuẩn của độ lệch chuẩn thực nghiệm |
THƯ MỤC TÀI LIỆU THAM KHẢO
[1] CIPM (1980), BIPM Proc-Verb. Com. Int. Poids et Mesures 48, C1-C30 (tiếng Pháp); BIPM (1980), Rapport BIPM-80/3, Report on the BIPM enquiry on error statements (Báo cáo về điểm hỏi đáp của BIPM các tuyến bố về sai số), Bur. Intl. Poids et Mesures (Sèvres, Pháp) (tiếng Anh)
[2] KAARLS, R. (1981), BIPM Proc-Verb. Com. Int. Poids et Mesures 49. A1-A12 (tiếng Pháp); Giacomo, P. (1981), Metrologia 17, 73-74 (tiếng Anh)
CHÚ THÍCH: Bản dịch tiếng Anh của Khuyến khích INC-1 (1980) được cho trong Lời giới thiệu của tiêu chuẩn này (xem 0.7) là bản cuối của Khuyến nghị này và được lấy từ báo cáo quốc tế của BIPM. Nó phù hợp với bản chính thức bằng tiếng Pháp của Khuyến nghị được cho trong BIPM Proc.-Verb. Com. Int. Poids et Mesures 49. Bản dịch tiếng Anh của Khuyến nghị INC-1 (1980) được cho trong Metrologia 17 là dự thảo và hơi khác với bản dịch được nêu trong báo cáo quốc tế BIPM và như trong 0.7.
[3] CIPM (1981), BIPM Proc.-Verb. Com. Int. Poids et Mesures 49, 8-9, 26 (tiếng Pháp); Giacomo, P. (1982), Metrologia 18, 43-44 (tiếng Anh).
[4] CIPM (1986), BIPM Proc.-Verb. Com. Int. Poids et Mesures 54, 14,35 (tiếng Pháp); Giacomo, P. (1987), Metrologia 24, 49-50 (tiếng Anh).
[5] ISO 5725:1986*, Precision of test methods – Determination of repeatability and reproducibility for a standard test method by inter-laboratory tests, Tổ chức tiêu chuẩn hóa quốc tế (Geneva, Thụy Sỹ) (Độ chụm của phương pháp thử – Xác định độ lặp lại và độ tái lặp đối với phương pháp thử chuẩn bằng thử nghiệm liên phòng).
CHÚ THÍCH: Tiêu chuẩn này hiện nay đã bị hủy. Bản soát xét có tên mới, “Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo”, và gồm có sáu phần.
[6] International vocabulary of basic and general terms in metrology, bản in lần hai, 1993**, Tổ chức tiêu chuẩn hóa quốc tế (Geneva, Thụy Sỹ) (từ vựng quốc tế về thuật ngữ chung và cơ bản trong đo lường học)
Chữ viết tắt của tên từ tài liệu này là VIM.
CHÚ THÍCH 1: Định nghĩa của thuật ngữ cho trong phụ lục B được lấy từ bản soát xét của VIM bản cuối trước khi xuất bản.
CHÚ THÍCH 2: Xuất bản lần hai của VIM do Tổ chức Tiêu chuẩn hóa quốc tế (ISO) công bố với tên của bảy tổ chức dươi đây tham gia vào công tác của Nhóm Tư vấn kỹ thuật ISO 4 (TAG 4), nhóm này đã hỗ trợ việc xây dựng VIM: Viện cân đo quốc tế (BIPM), Ủy ban kỹ thuật điện quốc tế (IEC), Liên đoàn quốc tế về hóa học lâm sàng (IFCC), ISO, Liên đoàn quốc tế về hóa học tinh khiết và ứng dụng (IUPAC), Liên đoàn quốc tế về vật lý thuần túy và ứng dụng (IUPAC), và Tổ chức quốc tế về đo lường pháp định (OIML).
CHÚ THÍCH 3: Xuất bản lần thứ nhất của VIM do ISO công bố năm 1984 dưới tên của BIPM, IEC, ISO và OIML.
[7] ISO 3534-1:1993,* Statistics – Vocabulary and symbols – Part 1: Probability and general statistical terms, Tổ chức tiêu chuẩn hóa quốc tế (Geneva, Thụy Sỹ) (Thống kê học – Từ vựng và ký hiệu – Phần 1: Thuật ngữ thống kê chung và thuật ngữ dùng trong xác suất)
[8] FULLER, W.A. (1987), Measurement error models, John Wiley (New York, N.Y.) [9] ALLAN, D.W. (1987), IEEE Trans. Instrum. Meas. IM-36, 646-654 (Các mô hình sai số của phép đo)
[10] DIETRICH, C.F. (1991), Uncertainty, calibration and probability, xuất bản lần hai, Adam-Hilger (Bristol) (Độ không đảm bảo, hiệu chuẩn và xác suất)
[11] MULLER, J.W. (1979), Nucl. Instrum. Meth. 163, 241-251.
[12] MULLER, J.W. (1984), Precision measurement and fundamental constants II, Taylor, B. N., and Phillips, W.D., eds, Natl. Bur. Stand. (U.S) Spec. Publ. 617, US GPO (Washington, D.C.), 375-381 (Phép đo độ chính xác và hằng số cơ bản)
[13] JEFFREYS, H. (1983), Theory of probability, bản in lần ba, Oxford University Press (Oxford) (Lý thuyết về xác suất)
[14] PRESS, S.J. (1989), Bayesian statistics: principles, models, and applications, John Wiley (New York, N.Y.) (Thống kê Bayesian: Nguyên tắc, mô hình và áp dụng)
[15] BOX, G.E.P., HUNTER, W.G., and HUNTER, J.S. (1978), Statistics for experimenters, John Wiley (New York, N.Y). (Thống kê đối với nhà thực nghiệm).
[16] WELCH, B.L. (1936), J. R. Stat. Soc. Suppl. 3, 29-48; (1938), Biometrika 29, 350-362; (1947), ibid. 34, 28-35.
[17] FAIRFIELD-SMITH, H. (1936), J. Counc. Sci. Indust. Res. (Australia) 9(3), 211.
[18] SATTERTHWAITE, F.E. (1941), Psychometrika 6, 309-316; (1946) Biometrics Bull. 2(6), 110-114
[19] ISO Guide 35:1989, ** Certification of reference material – General and statistical principles, bản in lần hai, Tổ chức tiêu chuẩn hóa quốc tế (Geneva, Thụy Sỹ) (Chứng nhận mẫu chuẩn – nguyên tắc chung và nguyên tắc thống kê)
[20] BARKER, T.B. (1985), Quality by experimental design, Marcel Dekker (New York, N.Y.) (Chất lượng do thiết kế thực nghiệm).
MỤC LỤC TRA CỨU THEO BẢNG CHỮ CÁI
A
ANOVA 4.2.8, H.5
ảnh hưởng hệ thống 3.2.3, 3.2.4, 3.3.1, 3.3.2, 3.3.3, D.6.1, E.1.1, E.3, E.4.4
ảnh hưởng ngẫu nhiên 3.2.2, 3.3.1, 3.3.3, 4.2.2, E.1.1, E.3
B
báo cáo độ không đảm bảo 7
báo cáo độ không đảm bảo chuẩn tổng hợp 7.2.1, 7.2.2
báo cáo độ không đảm bảo mở rộng 7.2.3, 7.2.4
bản chất của độ không đảm bảo D.3.4
bậc tự do 4.2.6, C.2.31, E.4.3, G, G.3, G.3.2, G.3.3, G.6.3, G.6.4
bậc tự do hiệu dụng 6.3.3, G.4, G.4.1, G.5.4, G.6.2
bậc tự do hiệu dụng của thành phần loại A 7.2.1, G.4.1 Chú thích 3
Bậc tự do hiệu chuẩn của thành phần loại B 7.2.1, G.4.1 Chú thích 3
bậc tự do của ước lượng đóng góp của phương sai (hoặc độ lệch chuẩn thực nghiệm góp phần H.1.6, H.3.6 Chú thích
bậc tự do của độ không đảm bảo chuẩn loại A G.3.3, G.6.3, G.6.4
bậc tự do của độ đảm bảo chuẩn Loại B G.4.2, G.4.3, G.6.3, G.6.4
biến C.2.2
biến ngẫu nhiên 4.1.1 Chú thích 1, 4.2.1, 4.2.3 Chú thích 1, C.2.2, C.3.1, C.3.2, C.3.4, C.3.7, C.3.8, E.3.4, F.1.2.1, G.3.2.
biến ngẫu nhiên trung tâm C.2.10.
BIPM 0.5, 7.1.1, A.1, A.2
biểu đồ tần số 4.4.3, D.6.1 Chú thích 1
bỏ qua một thành phần của độ không đảm bảo 3.4.4
bỏ qua sự hiệu chính 3.2.4 Chú thích 2, 3.4.4, 6.3.1 Chú thích, F.2.4.5.
C
cặp quan trắc đồng thời độc lập 5.2.3, C.3.4, F.1.2.2, H.2.2, H.2.4, H.4.2
chất lượng và tính khả dụng của độ không đảm bảo trích dẫn 3.4.8
chuỗi hiệu chuẩn 4.2.8 Chú thích
chuỗi Taylor 5.1.2, E.3.1, G.1.5, G.4.2, H.1.7, H.2.4
chứng nhận mẫu chuẩn H.5, H.5.3.2
CIPM 0.5, 6.1.1, 6.1.2, A.1, A.2, A.3
con số có ý nghĩa đối với hệ số tương quan 7.2.6
công thức Welch-Satterthwaite G.4.1, G.4.2, G.6.2, G.6.4
D
đại lượng ảnh hưởng ngẫu nhiên F.1.1.3, F.1.1.4
đại lượng ảnh hưởng 3.1.5, 3.1.6, 3.2.3, 4.2.2, B.2.10
đại lượng có thể đo được B.2.1
đại lượng có thể chuyển giao đối với trình bày độ không đảm bảo 0.4
đại lượng cụ thể 3.1.1, B.2.1 Chú thích 1
đại lượng của phân bố t G.3.4 Chú thích
đại lượng đầu vào 4.1.2
đại lượng đầu vào, các giới hạn xem các giới hạn đối với đại lượng đầu vào
đại lượng đầu ra 4.1.2
đại lượng đo 1.2, 3.1.1., 3.1.3, B.2.19, D.1, D.1.1, D.1.2, D.3.4
đại lượng được kiểm soát F.2.4.3
đại lượng nhất quán nội tại đối với sự trình bày độ không đảm bảo 0.4
đại lượng thu được D.2, D.2.1, D.3.1, D.3.2, D.3.3, D.4
đánh giá Loại A hiệp phương sai 5.2.3
đánh giá Loại A độ không đảm bảo 2.3.2, 3.3.3, 3.3.4, 3.3.5, 4.1.6, 4.2, 4.2.1, 4.2.2, 4.2.3, 4.2.4, 4.2.5, 4.2.6, 4.2.7, 4.2.8, 4.3.2, 4.4.1, 4.4.2, 4.4.3, E.3.7, F.1, F.1.1.1, F.1.1.2, F.1.1.3, F.1.1.4
đại lượng Loại B hiệp phương sai 5.2.5
đánh giá Loại B độ không đảm bảo 2.3.3, 3.3.3, 3.3.4, 3.3.5, 4.1.6, 4.3, 4.3.1, 4.3.2, 4.3.3, 4.3.4, 4.3.5, 4.3.6, 4.3.7, 4.3.8, 4.3.9, 4.3.10, 4.3.11, 4.4.4, 4.4.5, 4.4.6, E.3.7, F.2
đánh giá thống kê độ không đảm bảo do thay đổi đại lượng đầu vào 3.4.1, 3.4.2, 4.2.8, F.2.1, H.5.3.3
đạo hàm riêng 5.1.3
đặc trưng C.2.15
điều kiện lặp lại 3.1.4, B.2.15 Chú thích 1
định nghĩa hay quy định của đại lượng do xem đại lượng đo
định luật lan truyền độ không đảm bảo 3.3.6, 3.4.1, 5.1.2, E.3, E.3.1, E.3.2, E.3.6, G.6.6
định luật lan truyền sai số 5.2.2, Chú thích 1, E.3.2
định lý giới hạn trung tâm G.1.6, G.2, G.2.1, G.2.2, G.2.3, G.6.2, G.6.5, G.6.6
đo lường pháp định 3.4.5
độ chính xác của phép đo 3.1.3, 3.4.1, B.2.14.
độ lệch 3.2.3 Chú thích
độ không đảm bảo mở rộng 2.3.5, 3.3.7, 6, 6.2.1, 6.2.2, 6.2.3, G.1.1, G.2.3, G.3.2, G.4.1, G.5.1, G.5.2, G.5.3, G.5.4, G.6.4, G.6.5, G.6.6
độ không đảm bảo mở rộng đối với phân bố bất đối xứng G.5.3
độ không đảm bảo mở rộng tương đối 7.2.3
độ chụm B.2.14 Chú thích 2
độ lặp lại của kết quả đo B.2.15
độ tái lập của kết quả đo B.2.16.
độ không đảm bảo chuẩn 2.3.1, 3.3.5, 3.3.6, 4.1.5, 4.1.6, 4.2.3, D.6.1, E.4.1.
độ không đảm bảo an toàn E.1.1, E.1.2, E.2.1, E.2.3, E.4.1, F.2.3.2
độ không đảm bảo đo 0.1, 0.2, 1.1, 2.2, 2.2.1, 2.2.2, 2.2.3, 2.2.4, 3.3, 3.3.1, 3.3.2, B.2.18, D, D.5, D.5.1, D.5.2, D.5.3, D.6.1, D.6.2.
độ không đảm bảo của mẫu F.2.6
độ không đảm bảo của phương pháp đo F.2.5, F.2.5.1
độ không đảm bảo của độ lệch chuẩn thực nghệm của trung bình 4.3.2 Chú thích, E.4.3
độ không đảm bảo của sự hiệu chính 3.2.3 Chú thích, 3.3.1, 3.3.3, D.6.1, E.1.1, E.3
độ không đảm bảo của quan trắc đơn thiết bị được hiệu chuẩn F.2.4.1
độ không đảm bảo của quan trắc đơn thiết bị được kiểm định F.2.4.2
độ không đảm bảo chuẩn loại A 3.3.5, 4.2.3, C.3.3.
độ không đảm bảo chuẩn tổng hợp Loại A 7.2.1, G.4.1 Chú thích 3
độ không đảm bảo chuẩn Loại B 3.3.5, 4.3.1, C.3.3
độ không đảm bảo chuẩn tổng hợp từ các thành phần Loại A 7.2.1, G.4.1, Chú thích 3
độ không đảm bảo chuẩn tổng hợp từ các thành phần Loại B 7.2.1, G.4.1, Chú thích 3.
độ không đảm bảo chuẩn tương đối 5.1.6
độ không đảm bảo chuẩn tổng hợp 2.3.4, 3.3.6, 4.1.5, 5, 5.1.1, 5.1.2, 5.1.3, 5.1.6, 5.2.2, 6.1.1, D.6.1, E.3.6
độ không đảm bảo chuẩn tổng hợp tương đối 5.1.6, 7.2.1
độ không đảm bảo chuẩn tổng hợp và Ủy ban Tư vấn 6.1.1, A.3
độ không đảm bảo chuẩn tổng hợp và so sánh quốc tế 6.1.1, A.3
độ không đảm bảo do định nghĩa không đầy đủ đại lượng đo 3.1.3 Chú thích, D.1.1, D.3.4, D.6.2
độ không đảm bảo do độ chụm hạn chế số học F.2.2.3
độ không đảm bảo do lấy mẫu giới hạn 4.3.2 Chú thích, E.4.3
độ không đảm bảo do độ phân giải của chỉ thị hiện số F.2.2.1
độ không đảm bảo do độ trễ F.2.2.2
độ không đảm bảo khi không áp dụng sự hiệu chính 3.4.4, 6.3.1 Chú thích, F.2.4.5
độ không đảm bảo nhỏ nhất D.3.4
độ không đảm bảo lớn nhất cho phép F.2.4.2
độ không đảm bảo tổng thể 2.3.5 Chú thích 3
độ lệch chuẩn là thước đo độ không đảm bảo E.3.2, E.4, E.4.1, E.4.2, E.4.3, E.4.4
độ lệch chuẩn 3.3.5, C.2.12, C.2.21, C.3.3
độ lệch chuẩn thực nghiệm 4.2.2, B.2.17.
độ lệch chuẩn thực nghiệm của trung bình 4.2.3, B.2.17 Chú thích 2
đường cong hiệu chuẩn F.2.4.2, F.2.4.5
đường cong hiệu chuẩn tuyến tính H.3
G
giá trị của đại lượng 3.1.1, 3.1.2, 3.1.3, B.2.2
giá trị thực của đại lượng 2.2.4, 3.1.1 Chú thích, B.2.3, D, D.3, D.3.1, D.3.4, D.3.5, E.5.1, E.5.2, E.5.3, E.5.4
giá trị thực quy ước của đại lượng B.2.4
giá trị hoặc đại lượng đầu vào được đưa vào F.2.3, F.2.3.1
giá trị thực nghiệm của hiệp phương sai 5.2.5, C.3.6 Chú thích 3
giới hạn an toàn 6.3.1 Chú thích
giới hạn cực đại xem giới hạn với đại lượng đầu vào
giới hạn với đại lượng đầu vào 4.3.7, 4.3.8, 4.3.9, 4.4.5, 4.4.6, F.2.3.3
giới hạn, trên và dưới, với đại lượng đầu vào xem giới hạn với đại lượng đầu vào
H
hàm khối lượng xác suất C.2.6
hàm phân bố C.2.4
hàm ước lượng 4.2.7, C.2.25
hệ đơn vị quốc tế (SI) 0.3, 3.4.6
hiệu chính 3.2, 3.2.3, 3.2.4 Chú thích 2, B.2.23
hiểu chuẩn, sự so sánh 1.2.3 Chú thích
hệ số hiệu chính 3.2.3, B.2.24
hệ số độ nhạy 5.1.3, 5.1.4
hệ số phủ 2.3.6, 3.3.7, 4.3.4 Chú thích, 6.2.1, 6.3, G.1.3, G.2.3, G.3.4, G.6.1
hệ số t E.3.3, G.3.2, G.3.4, G.4.1, G.5.4, G.6.2, G.6.4, G.6.5, G.6.6
hệ số tin cậy C.2.29
hệ số tương quan 5.2.2, 5.2.3, C.3.6, F.1.2.3, H.2.3, H.2.4, H.3.2, H.4.2
hệ thống 3.3.3, E.1.3, E.3.4, E.3.5, E.3.6, E.3.7
Hiệp hội quốc tế về hóa học tinh khiết và hóa học ứng dụng xem IUPAC
hiệp phương sai 3.3.6, 5.2.2, C.3.4, F.1.2.1, F.1.2.2, F.1.2.3, F.1.2.4
hiệp phương sai của đại lượng đo liên quan xem ước lượng hoặc đại lượng đầu vào có tương quan
hiệp phương sai của hai trung bình số học 5.2.3, C.3.4, H.2.2, H.2.4, H.4.2
hiệp phương sai tương đối của đại lượng đo xem ước lượng hoặc đại lượng đầu vào có tương quan
I
IEC A.3, B.1
IFCC B.1
ISO A.3, B.1
ISO 3534-1 2.1, C.1
IUPAC B.1
IUPAP B.1
K
kết quả của phép đo 1.3, 3.1.2, B.2.11
kết quả chưa được hiệu chính B.2.12
kết quả và độ không đảm bảo đo, tính sẵn có của thông tin mô tả 7.1.1, 7.1.3
kết quả và độ không đảm bảo đo, cách thức báo cáo 7.2.2, 7.2.4
kết quả và độ không đảm bảo đo, báo cáo chi tiết 7.1.4, 7.2.7
khoảng dung sai thống kê C.2.30 Chú thích 2
khoảng phủ thống kê C.2.30
khoảng tin cậy 4.2.3 Chú thích 1, 6.2.2, C.2.27, C.2.28, E.3.3
khoản tin cậy một phía C.2.28
khoảng tin cậy hai phía C.2.27
Khuyến nghị INC-1 (1980) 0.5, 0.7, 3.3.3, 6.1.1, 6.1.2, 6.3.3, A.1, A.3, E, E.2.3, E.3.7
Khuyến nghị 1 (CI-1981), CIPM 0.5, 6.1.1, A.2, A.3
Khuyến nghị 1 (CI-1986), CIPM 0.5, 6.1.1, 6.1.2, A.3
Khuyến nghị 1 (CI-1986), CIPM 0.5, 6.1.1, A.2, A.3
kiểm soát thống kê 3.4.2, 4.2.4
kỳ vọng (hay giá trị được kỳ vọng) 3.2.2, 3.2.3, 4.1.1 Chú thích 3, 4.2.1, 4.3.7, 4.3.8, 4.3.9, C.2.9, C.3.1, C.3.2
L
làm tròn độ không đảm bảo 7.2.6
Liên đoàn quốc tế về hóa học y học và y học phòng thí nghiệm xem IFCC
Liên đoàn quốc tế về vật lý thuần túy và ứng dụng xem IUPAP
loại trừ sự tương quan 5.2.4, 5.2.5, F.1.2.4, H.3.5
M
ma trận hệ số tương quan 7.2.5, C.3.6 Chú thích 2
ma trận hiệp phương sai 3.1.7, 5.2.2 Chú thích 2, 7.2.5, C.3.5, H.2.3.
mômen trung tâm của bậc q C.2.13, C.2.22, E.3.1 Chú thích 1
mức tin cậy 0.4, 2.2.3 Chú thích 1, 2.3.5 Chú thích 1 và 2, 3.3.5, 3.3.7, 4.3.4, 6.2.2, 6.2.3, 6.3.1, 6.3.2, 6.3.3, C.2.29, E.3.5, E.4.4, E.5.2 Chú thích, G, G.1.1, G.1.2, G.1.3, G.2.3 G.3.2, G.3.4, G.4.1, G.6.1, G.6.4, G.6.6
mức tin cậy nhỏ nhất F.2.3.2
minh họa bằng đồ thị việc đánh giá độ không đảm bảo chuẩn 4.4.
N
ngẫu nhiên 3.3.3, E.1.3, E.3.5, E.3.6, E.3.7
nhầm lẫn giữa sai số và độ không đảm bảo 3.2.2 Chú thích 2, 3.2.3 Chú thích, E.5.4
nhiều giá trị của đại lượng đo D.6.2
Nhóm công tác về công bố độ không đảm bảo 0.5, 3.3.3, 6.1.1, 6.1.2, A.1, A.2, A.3
nhu cầu đánh giá Loại B F.2.1
nguồn của độ không đảm bảo 3.3.2
nguyên tắc của entropi cực đại 4.3.8 Chú thích 2
nguyên tắc của phép đo B.2.6
O
OIML A.3, B.1
P
phân bố bất đối xứng 4.3.8, F.2.4.4, G.5.3
phân bố chữ nhật 4.3.7, 4.3.9, 4.4.5, F.2.2.1, F.2.2.2, F.2.2.3, F.2.3.3, G.2.2 Chú thích 1, G.4.3
phân bố chuẩn 4.2.3 Chú thích 1, 4.3.2 Chú thích, 4.3.4, 4.3.5, 4.3.6, 4.3.9 Chú thích 1, 4.4.2, 4.4.6, C.2.14, E.3.3, F.2.3.3, G.1.3, G.1.4, G.2.1, G.2.2, G.2.3, G.5.2 Chú thích 2.
phân bố F H.5.2.3
phân bố Laplace-Gauss C.2.14
phân bố Laplace-Gauss F xem phân bố
phân bố Student C.3.8, G.3.2
phân bố t 4.2.3 Chú thích 1, C.3.8, G.3, G.3.2, G.3.4, G.4.1, G.4.2, G.5.4, G.6.2
phân bố tần số 3.3.5, 4.1.6, C.2.18, E.3.5
phân bố tiên nghiệm 4.1.6, 4.3.1 Chú thích, 4.4.4, D.6.1, E.3.4, E.3.5, G.4.2, G.4.3
phân bố tam giác 4.3.9, 4.4.6, F.2.3.3
phân bố toán xác định F.2.2
phân bố xác suất 3.3.4, 4.1.1, Chú thích 1, 4.1.6, 4.2.3 Chú thích 1, 4.4.1, 4.4.2, 4.4.3, 4.4.4, C.2.3, E.4.2, G.1.4, G.1.5
phân bố xác suất chập 4.3.9, Chú thích 2, G.1.4, G.1.5, G.1.6, G.2.2, G.6.5
phân loại thành phần độ không đảm bảo 3.3.3, 3.3.4, E.3.6, E.3.7
phân nhóm các thành phần của độ không đảm bảo 3.3.3 Chú thích, 3.4.3, E.3.7
phân tích phương sai xem ANOVA
phân tích sai số 0.2
phần tử xác suất C.2.5 Chú thích, F.2.4.4
phép đo tốt nhất có thể có của đại lượng đo D.3.4
phép đo 3.1, 3.1.1, B.2.5
phép đo, mô hình toán 3.1.6, 3.4.1, 3.4.2, 4.1, 4.1.1, 4.1.2
phép đo, vai trò của ANOVA H.5.3
phép đo, độ chụm, nguyên tắc của tiêu chuẩn này áp dụng 1.1
phép đo, phương pháp 3.1.1, B.2.7
phép thử F H.5.2.2, H.5.2.4
phương pháp bình phương nhỏ nhất 4.2.5, G.3.3, H.3, H.3.1, H.3.2
phương pháp đo, đơn vị phụ thuộc H.6
phương pháp lý tưởng đối với sự đánh giá và trình bày độ không đảm bảo 0.4
phương pháp phổ quát đối với việc đánh giá và trình bày độ không đảm bảo 0.4
phương sai 3.1.7, 4.2.2, 4.2.3, C.2.11, C.2.20, C.3.2
phương sai Allan 4.2.7 Chú thích
phương sai của trung bình 4.2.3, C.3.2
phương sai Loại A 4.2.3
phương sai Loại B 4.3.1
phương sai ngẫu nhiên có tương quan 4.2.7
phương sai thực nghiệm của trung bình 4.2.3, C.3.2
phương sai thực nghiệm (hoặc ước lượng) 4.2.2, H.3.6 Chú thích
phương sai tổng hợp 3.3.6, 5.1.2
phương sai tổng hợp tương đối 5.1.6
phương sai tương đối 5.1.6
Q
quan hệ hàm số 4.1.1, 4.1.2
quan hệ hàm số phi tuyến tính 4.1.4 Chú thích, 5.1.2 Chú thích, F.2.4.4 Chú thích, G.1.5, H.1.7, H.2.4
quan trắc lặp lại 3.1.4, 3.1.5, 3.1.6, 3.2.2, 3.3.5, 4.2.1, 4.2.3, 4.3.1, 4.4.1, 4.4.3, 5.2.3, E.4.2, E.4.3, F.1, F.1.1, F.1.1.1, F.1.1.2, G.3.2
S
sai lầm 3.4.7
sai số, cách xác định 3.4.5
sai số của phép đo 0.2, 2.2.4, 3.2, 3.2.1 Chú thích, 3.2.2 Chú thích 2, 3.2.3 Chú thích, 3.3.1 Chú thích, 3.3.2, B.2.19, D, D.4, D.6.1, D.6.2, E.5.1
sai số, đường cong sai số của phương tiện được kiểm định F.2.4.2
sai số, giới hạn tối đa E.4.1
sai số hệ thống 3.2.1, 3.2.3, B.2.22
sai số ngẫu nhiên 3.2.1, 3.2.2, 3.2.3, B.2.21
sai số tối đa cho phép F.2.4.2
sai số tương đối B.2.20
so sánh hai quan điểm về độ không đảm bảo E.5
số hạng bậc cao 5.1.2 Chú thích, E.3.1, H.1.7
sơ đồ phép đo 7.1.1
sự độc lập 5.1, C.3.7
sự lan truyền độ lệch chuẩn E.3, E.3.1, E.3.2
sự lan truyền nhiều độ lệch chuẩn E.3.3
sự lan truyền khoảng tin cậy E.3.3
sự lặp lại độc lập F.1.1.2
sự ngẫu nhiên F.1.1, F.1.1.3, F.1.1.4, F.1.1.5
sự tuyến tính hóa đối với quan hệ hàm số 5.1.5, F.2.4.4 Chú thích, 5.1.6 Chú thích 1
sự tương quan 5.1, 5.2, C.2.8, F.1.2, F.1.2.1, F.1.2.2, F.1.2.3, F.1.2.4
sự ước lượng C.2.24
sử dụng giá trị được thừa nhận của chuẩn đo lường như một đơn vị 3.4.6, 4.2.8 Chú thích
T
tần số C.2.17
tần số tương đối E.3.5
tập hợp thông tin đối với đánh giá Loại B 3.3.5 Chú thích, 4.3.1, 4.3.2, 5.2.5
tham số C.2.7
thiết kế lồng ổn định H.5.3.1, H.5.3.2
thiếu báo cáo rõ ràng về độ không đảm bảo 7.1.3
thống kê 4.2.7, C.2.23
thủ tục đo 3.1.1, 7.1.2, B.2.8, F.1.1.2
tích chập xem xác suất
tính hai lần độ không đảm bảo 4.3.10
tính toán bằng số độ không đảm bảo chuẩn tổng hợp 5.1.3 Chú thích 2, 5.2.2 Chú thích 3
tóm tắt thủ tục đánh giá và trình bày độ không đảm bảo 8
Tổ chức quốc tế về đo lường pháp định xem OIML
Tổ chức tiêu chuẩn hóa quốc tế xem ISO
tổng thể C.2.16
trung bình C.2.9, C.3.1
trung bình cộng 4.1.4 Chú thích, 4.2.1, C.2.19
Từ vựng quốc tế các thuật ngữ chung và cơ bản trong đo lường học xem VIM
U
Ủy ban cân và đo quốc tế xem CIPM
Ủy ban kỹ thuật điện xem IEC
Ư
ước lượng 3.1.2, C.2.26
ước lượng đầu vào 4.1.4, 4.1.6, 4.2.1
ước lượng đầu vào, sự phân loại 4.1.3
ước lượng đầu ra 4.1.4, 4.1.5, 7.2.5
ước lượng độ không đảm bảo, minh họa thực tế E.2, E.2.1, E.2.2, E.2.3
ước lượng hoặc đại lượng đầu vào có tương quan xem sự tương quan
ước lượng hoặc đại lượng đầu ra có tương quan xem sự tương quan
ước lượng hoặc đại lượng đầu ra có tương quan xem sự tương quan 3.1.7, 7.2.5, H.2.3, H.2.4, H.3.2, H.4.2
ước lượng tích lũy của phương sai (hoặc độ lệch chuẩn thực nghiệm tích lũy) 4.2.4, 4.2.8 Chú thích, H.1.3.2, H.3.6 Chú thích, H.5.2.2, H.5.2.5, H.6.3.1, H.6.3.2 Chú thích
V
Viện cân đo quốc tế xem BIPM
VIM 2.1, 2.2.3, 2.2.4, B.1
X
xác định hệ số độ nhạy bằng thực nghiệm 5.1.4
xác suất 3.3.5, 4.3.7, 4.3.8, 4.3.9, C.2.1, E.3.5, E.3.6, F.2.2.3
xác suất chủ quan 3.3.5, D.6.1
xác suất phủ 0.4, 2.3.5 Chú thích 1, 3.3.7, 6.2.2, G.1.1, G.1.3, G.3.2.
MỤC LỤC
Lời nói đầu
Lới giới thiệu
1. Phạm vi áp dụng
2. Thuật ngữ và định nghĩa
2.1. Thuật ngữ chung về đo lường
2.2. Thuật ngữ “độ không đảm bảo”
2.3. Thuật ngữ riêng của tiêu chuẩn này
3. Các khái niệm cơ bản
3.1. Phép đo
3.2. Sai số, ảnh hưởng và hiệu chính
3.3. Độ không đảm bảo
3.4. Xem xét thực tế
4. Đánh giá độ không đảm bảo chuẩn
4.1. Lập mô hình phép đo
4.2. Đánh giá độ không đảm bảo chuẩn loại A
4.3. Đánh giá độ không đảm bảo chuẩn loại B
4.4. Minh họa bằng đồ thị đánh giá độ không đảm bảo chuẩn
5. Xác định độ không đảm bảo chuẩn tổng hợp
5.1. Đại lượng đầu vào không tương quan
5.2. Các đại lượng đầu vào tương quan
6. Xác định độ không đảm bảo mở rộng
6.1. Giới thiệu
6.2. Độ không đảm bảo mở rộng
6.3. Lựa chọn hệ số phủ
7. Báo cáo độ không đảm bảo
7.1. Hướng dẫn chung
7.2. Hướng dẫn cụ thể
8. Tóm tắt thủ tục đánh giá và trình bày độ không đảm bảo
Phụ lục A (tham khảo) Khuyến nghị của Nhóm công tác và CIPM
Phụ lục B (tham khảo) Thuật ngữ chung về đo lường
Phụ lục C (tham khảo) Thuật ngữ và khái niệm thống kê cơ bản
Phụ lục D (tham khảo) Giá trị “thực”, sai số và độ không đảm bảo
Phụ lục E (tham khảo) Động lực và cơ sở cho Khuyến nghị INC-1 (1980)
Phụ lục F (tham khảo) Hướng dẫn thực hành về đánh giá thành phần độ không đảm bảo
Phụ lục G (tham khảo) Bậc tự do và mức tin cậy
Phụ lục H (tham khảo) Ví dụ
Phụ lục J (tham khảo) Bảng chú giải các ký hiệu quan trọng
Thư mục tài liệu tham khảo
Mục lục tra cứu theo bảng chữ cái
* Tài liệu này hiện đã được thay thế bằng ISO/IEC Guide 99:2007 và được chấp nhận thành TCVN 6165:2009, Từ vựng quốc tế về đo lường học – Khái niệm, thuật ngữ chung và cơ bản (VIM).
1) Bộ ISO 31 đã được thay thế bằng bộ ISO 80000 và IEC 80000, và đã được chấp nhận thành bộ TCVN 7870.
2) Tiêu chuẩn này hiện đã bị hủy bỏ và được thay thế bằng ISO/IEC Guide 99:2007 và được chấp nhận thành TCVN 6165:2010.
* ISO 3534-1:1993 đã bị hủy bỏ và thay thế bằng ISO 3534-1:2006 và được chấp nhận thành TCVN 8244-1:2010. Chú ý rằng một số thuật ngữ và định nghĩa đã được soát xét lại. Để biết thêm thông tin, xem lần xuất bản mới nhất.
* Nếu trong định nghĩa momen, các đại lượng: X, X – a, Y, Y – b, … được thay bằng giá trị tuyệt đối của chúng, ví dụ |X|,|X – a|,|Y|,|Y – b|, … thì các mômen khác được gọi là “mômen tuyệt đối” được xác định.
* ISO 5725:1986 đã được thay thế bằng bộ tiêu chuẩn có sáu phần và được chấp nhận thành bộ tiêu chuản TCVN 6910. Bộ TCVN 6910 gồm các tiêu chuẩn sau đây, có tên chung Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo:
Phần 1: Nguyên tắc chung và định nghĩa
Phần 2: Phương pháp cơ bản xác định độ lặp lại và độ tái lập của phương pháp đo tiêu chuẩn
Phần 3: Thước đo trung gian độ chụm của phương pháp đo tiêu chuẩn
Phần 4: Phương pháp cơ bản xác định độ đúng của phương pháp đo tiêu chuẩn
Phần 5: Phương pháp khác xác định độ chụm của phương pháp đo tiêu chuẩn
Phần 6: Sử dụng giá trị độ chính xác trong thực tế.
** Tài liệu này hiện đã được thay thế bằng ISO/IEC Guide 99:2007 và được chấp nhận thành TCVN 6165:2009, Từ vựng quốc tế về đo lường học – Khái niệm, thuật ngữ chung và cơ bản (VIM)
* ISO 3534-1:2006 hủy bỏ, thay thế ISO 3534-1:1993 và đã được chấp nhận thành TCVN 8244-2010. Chú ý rằng một số thuật ngữ và định nghĩa đã được soát xét. Để có thêm thông tin, xem bản in mới nhất.
** ISO Guide 35:2006 hủy bỏ, thay thế ISO Guide 35:1989 và đã được chấp nhận thành TCVN 8245:2009. Để có thêm thông tin, xem bản in mới nhất.