Quy chuẩn QCVN4:2016/BQP

QCVN 4 : 2016/BQP

QUY CHUẨN KỸ THUẬT QUỐC GIA VỀ MÃ HÓA DỮ LIỆU SỬ DỤNG TRONG LĨNH VỰC NGÂN HÀNG

National technical regulation on data encryption used in banking

MỤC LỤC

Lời nói đầu

1. QUY ĐỊNH CHUNG

1.1. Phạm vi điều chỉnh

1.2. Đối tượng áp dụng

1.3. Tài liệu viện dẫn

1.4. Thuật ngữ và định nghĩa

1.5. Các ký hiệu

2. QUY ĐỊNH KỸ THUẬT

2.1. Quy định chung

2.2. Mã khối

2.2.1. TDEA – Thuật toán mã dữ liệu bội ba

2.2.2. AES

2.2.3. Camellia

2.3. Chế độ hoạt động của mã khối

2.3.1. Chế độ xích liên kết khối mã CBC (Cipher Block Chaining)

2.3.2. Chế độ phản hồi mã CFB (Cipher FeedBack)

2.3.3. Chế độ phản hồi đầu ra OFB (Output Feedback):

2.3.4. Chế độ đếm CTR (Counter)

2.4. Mã dòng

3. QUY ĐỊNH VỀ QUẢN LÝ

4. TRÁCH NHIỆM CỦA TỔ CHỨC, CÁ NHÂN

5. TỔ CHỨC THỰC HIỆN

Phụ lục A (Quy định): Mô tả DES

Phụ lục B (Quy định): Các phép biến đổi của AES

 

Lời nói đầu

QCVN 4 : 2016/BQP do Cục Quản lý mật mã dân sự và Kiểm định sản phẩm mật mã – Ban Cơ yếu Chính phủ biên soạn, Ban Cơ yếu Chính phủ trình duyệt, Bộ Khoa học và Công nghệ thẩm định và được ban hành theo Thông tư số 161/2016/TT-BQP ngày 21 tháng 10 năm 2016 của Bộ trưởng Bộ Quốc phòng.

 

QUY CHUẨN KỸ THUẬT QUỐC GIA VỀ MÃ HÓA DỮ LIỆU SỬ DỤNG TRONG LĨNH VỰC NGÂN HÀNG

National technical regulation on data encryption used in banking

1. QUY ĐỊNH CHUNG

1.1. Phạm vi điều chỉnh

Quy chuẩn kỹ thuật quốc gia này quy định mức giới hạn về đặc tính kỹ thuật mật mã của các thuật toán mã hóa dữ liệu dùng trong các sản phẩm mật mã dân sự sử dụng trong lĩnh vực ngân hàng.

1.2. Đối tượng áp dụng

Quy chuẩn này áp dụng đối với các doanh nghiệp kinh doanh sản phẩm, dịch vụ mật mã dân sự trong lĩnh vực ngân hàng; các tổ chức tín dụng (trừ quỹ tín dụng nhân dân cơ sở có tài sản dưới 10 tỷ, tổ chức tài chính vi mô) sử dụng sản phẩm, dịch vụ mật mã dân sự.

1.3. Tài liệu viện dẫn

– Recommendation for Random Number Generation Using Deterministic Random Bit Generators, NIST SP 800-90A Rev. 1, National Institute of Standards and Technology, June 2015. (Khuyến cáo cho bộ sinh số ngẫu nhiên sử dụng bộ sinh bit ngẫu nhiên tất định, NIST SP 800-90A Rev. 1, Viện tiêu chuẩn và công nghệ quốc gia (Mỹ), tháng 6 năm 2015).

– TCVN 7876:2007 Công nghệ thông tin – Kỹ thuật mật mã – Thuật toán mã dữ liệu AES.

– TCVN 11367-3:2016 (ISO/IEC 18033-3:2010) Công nghệ thông tin – Các kỹ thuật an toàn – Thuật toán mật mã – Phần 3: Mã khối.

– ISO/IEC 10116:2006 Information technology – Security techniques – Modes of operation for an n-bit block cipher.

– ISO/IEC 9797-1:2011 Information technology – Security techniques – Message Authentication Codes (MACs) – Part 1: Mechanisms using a block cipher.

1.4. Giải thích từ ngữ

Trong Quy chuẩn này, các từ ngữ dưới đây được hiểu như sau:

1.4.1. Thông tin không thuộc phạm vi bí mật nhà nước

Là thông tin không thuộc nội dung tin “tuyệt mật”, “tối mật” và “mật” được quy định tại Pháp lệnh Bảo vệ bí mật nhà nước ngày 28 tháng 12 năm 2000.

1.4.2. Mật mã

Là những quy tắc, quy ước riêng dùng để thay đổi hình thức biểu hiện thông tin nhằm bảo đảm bí mật, xác thực, toàn vẹn của nội dung thông tin.

1.4.3. Mật mã dân sự

Là kỹ thuật mật mã và sản phẩm mật mã được sử dụng để bảo mật hoặc xác thực đối với thông tin không thuộc phạm vi bí mật nhà nước.

1.4.4. Sản phẩm mật mã dân sự

Là các tài liệu, trang thiết bị kỹ thuật và nghiệp vụ mật mã để bảo vệ thông tin không thuộc phạm vi bí mật nhà nước.

1.4.5. Kỹ thuật mật mã

Là phương pháp, phương tiện có ứng dụng mật mã để bảo vệ thông tin.

1.4.6. Mã hóa

Phép biến đổi (khả nghịch) dữ liệu bởi thuật toán mật mã để tạo ra bản mã, tức là giấu nội dung thông tin của dữ liệu.

1.4.7. Giải mã

Phép toán ngược với phép mã hóa tương ứng.

1.4.8. Mã khối

Hệ mật đối xứng với tính chất là thuật toán mã hóa thao tác trên một khối của bản rõ, nghĩa là trên một xâu bit có độ dài xác định, kết quả cho ra một khối của bản mã.

1.4.9. Mã dòng

Hệ mật đối xứng với tính chất là thuật toán mã hóa bao gồm tổ hợp một dãy các ký tự của bản rõ với dãy các ký tự của khóa dòng, mỗi lần một ký tự, sử dụng một hàm khả nghịch.

1.4.10. Khóa

Dãy các ký tự điều khiển sự vận hành của các thuật toán mật mã (ví dụ, phép mã hóa, giải mã).

1.4.11. Khóa dòng

Dãy các ký tự giả ngẫu nhiên bí mật, được sử dụng bởi các thuật toán mã hóa và giải mã của mã dòng.

1.5. Các ký hiệu

n	độ dài tính bằng bit của bản rõ/bản mã đối với mã khối
Ek	hàm mã hóa với khóa K
Dk	hàm giải mã với khóa K
Nr	số vòng của thuật toán AES, bằng 10,12 hoặc 14 để chọn độ dài khóa tương ứng 128, 192, hoặc 256 bit.
Nb	Số các cột (các từ 32 bit) tạo nên Trạng thái.
Å	phép toán logic XOR trên xâu bit, nghĩa là nếu A và B là hai xâu cùng độ dài thì A Å B là xâu bit bao gồm các bit là kết quả phép toán logic XOR của A và B
Ä	phép nhân hai đa thức (mỗi đa thức có bậc bé hơn 4) theo mod x4 + 1
Ù	phép toán logic AND trên xâu bit, nghĩa là nếu A và B là các xâu bit cùng độ dài, thì A Ù B là xâu bit được tạo từ phép toán logic AND các bit tương ứng của A và B.
Ú	phép toán logic OR trên xâu bit, tức nếu A và B là hai xâu bit cùng độ dài, thì A Ú B là xâu bit gồm các bit là kết quả của phép toán logic OR của A và B.
||	phép ghép các xâu bit
•	phép nhân trên trường hữu hạn
	phép dịch vòng sang trái i bit.
	phép dịch vòng sang phải i bit
	phép bù bit của x
a mod n	với các số nguyên a và n, a mod n ký hiệu số dư (không âm) trong phép chia a cho n. Một cách tương đương, b = a mod n nếu b là số nguyên duy nhất thỏa mãn các điều kiện sau:
	(i) 0 ≤ b <>
	(ii) (b – a) là bội số nguyên của n
	phép cộng trong số học mô-đun, nghĩa là nếu A và B là hai xâu t-bit thì AB được xác định bằng (A + B) mod 2t
	phép trừ trong số học mô-đun, nghĩa là nếu A và B là hai xâu t-bit thì A B được xác định bằng (A – B)mod 2t

2. QUY ĐỊNH KỸ THUẬT

2.1. Quy định chung

– Quy định chi tiết về nguồn ngẫu nhiên:

Các số ngẫu nhiên được sử dụng cho các mục đích khác nhau như để sinh các tham số mật mã, các khóa mật mã, các giá trị ngẫu nhiên dùng một lần và các giá trị thách đố xác thực.

Một số bộ sinh bit ngẫu nhiên tất định DRBG được chấp thuận để sử dụng theo quy định chung bao gồm: HASH_DRBG, HMAC_DRBG và CTR_DRBG.

Các bộ sinh bit ngẫu nhiên RBG tuân theo SP800-90A phiên bản sửa đổi lại năm 2015 để sinh bit ngẫu nhiên cũng được chấp thuận để sử dụng tiếp.

2.2. Mã khối

Trong Quy chuẩn này quy định 3 loại mã khối áp dụng cho việc mã hóa dữ liệu để bảo vệ thông tin trong lĩnh vực ngân hàng.

Độ dài khối	Tên thuật toán	Độ dài khóa quy định áp dụng
64 bit	TDEA	Không nhỏ hơn 192 bit
128 bit	AES	Không nhỏ hơn 256 bit
	Camellia	Không nhỏ hơn 256 bit

– Quy định về ngưỡng thời gian và độ an toàn khóa cụ thể:

Độ an toàn theo bít	Thuật toán mã khối	Thời gian sử dụng quy định
112	3TDEA	Đến cuối năm 2030
256	AES-256	Từ năm 2030
	Camellia-256

2.2.1. TDEA – Thuật toán mã dữ liệu bội ba

Trong Quy chuẩn này thuật toán mã dữ liệu bội ba (TDEA-Triple Data Encryption Algorithm) xử lý các khối dữ liệu 64 bit, sử dụng khóa mật mã có độ dài không nhỏ hơn 192 bit.

Phép mã hóa/giải mã TDEA là phép toán ghép các phép toán mã hóa và giải mã DES. Khóa của TDEA gồm ba khóa K1, K₂ và K₃ là những khóa DES khác nhau (K1 ≠ K₂, K₂ ≠ K₃, và K₃ ≠ K₁)

2.2.1.1. Phép mã hóa/giải mã TDEA

2.2.1.1.1. Các định nghĩa mã hóa /giải mã

TDEA được xác định theo thuật ngữ của phép toán của DES, ở đấy E_k là phép toán mã hóa của DES với khóa K và D_k là phép giải mã của DES với khóa K.

2.2.1.1.2. Phép mã hóa

Phép biến đổi khối P có độ dài 64 bit thành khối C có độ dài 64 bit được xác định như sau:

Phép mã hóa/giải mã DES được mô tả tại Phụ lục A của Quy chuẩn này.

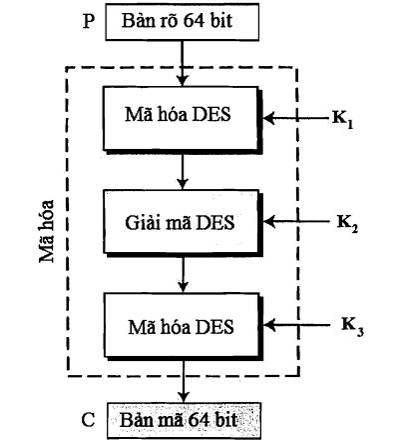
Hình 1: Sơ đồ phép mã hóa TDEA

2.2.1.1.3. Phép giải mã TDEA

Phép biến đổi khối C có độ dài 64 bit thành khối P có độ dài 64 bit được xác định như sau:

Phép mã hóa/giải mã DES được mô tả tại Phụ lục A của Quy chuẩn này.

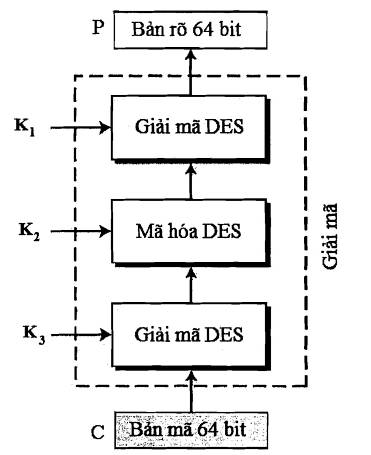
Hình 2: Sơ đồ phép giải mã TDEA

2.2.1.2. Chu trình khóa

Phần lược đồ khóa DES được mô tả tại Điều A.5.

2.2.1.3. Chế độ hoạt động của TDEA

Các chế độ hoạt động của TDEA được quy định tại Mục 2.3 của Quy chuẩn này.

2.2.1.4. Khóa

Độ dài khóa sử dụng trong mã khối TDEA được quy định:

Độ dài khối	Tên thuật toán	Độ dài khóa quy định áp dụng
64 bit	TDEA	Không nhỏ hơn 192 bit

2.2.1.4.1. Các yêu cầu về khóa

Đối với các chế độ hoạt động của mã khối TDEA, 3 khóa mật mã (K₁, K₂ và K₃) xác định khóa cho hệ mật TDEA cần:

a. Phải được giữ bí mật.

b. Được sinh ra sử dụng bộ sinh bit ngẫu nhiên được quy định trong phần 2.1 của Quy chuẩn này.

c. Là các khóa mật mã khác nhau.

d. Đảm bảo toàn vẹn mà mỗi khóa không bị thay đổi trái phép kể từ khi được sinh ra, gửi đi hoặc được lưu trữ bởi một thực thể có thẩm quyền.

e. Được sử dụng theo thứ tự thích hợp theo quy định bởi chế độ hoạt động riêng biệt.

f. Không sử dụng để mã hóa nhiều hơn 2³² khối dữ liệu 64-bit.

g. Không sử dụng các khóa yếu và bán yếu (Được quy định tại Điều 2.2.1.4.2).

2.2.1.4.2. Khóa yếu

Đối với thuật toán DES có một số khóa mật mã được coi là yếu khi sử dụng. Việc sử dụng các khóa yếu này ảnh hưởng đến độ an toàn của thuật toán TDEA. Các khóa yếu không được sử dụng trong thuật toán TDEA được liệt kê dưới đây (theo định dạng thập lục phân):

Một số cặp khóa khi mã hóa thì bản rõ và bản mã là giống hệt nhau và cũng không được sử dụng. Các khóa bán-yếu đó là (theo định dạng thập lục phân):

Ngoài ra còn 48 khóa sau chỉ tạo ra 4 khóa con khác nhau (thay vì 16 khóa con khác nhau) và cũng không được sử dụng. Đó là các khóa sau (theo định dạng thập lục phân):

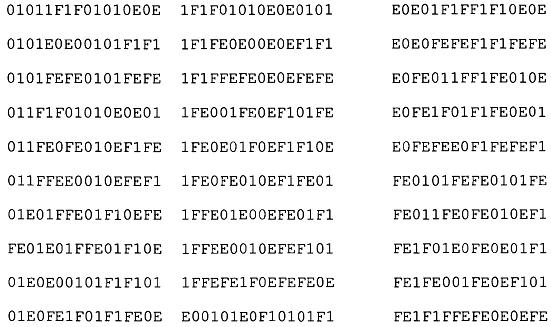
CHÚ THÍCH: Các khóa yếu và khóa bán-yếu được liệt kê ở trên được biểu diễn với tính lẻ và được chỉ ra trong phần ngoài cùng bên phải của mỗi byte.

2.2.2. AES

Đối với thuật toán AES, độ dài của khối đầu vào, khối đầu ra và Trạng thái đều là 128 bit. Như vậy Nb = 4 là số lượng các từ 32 bít (số cột) của Trạng thái.

Trong Quy chuẩn này thuật toán AES, độ dài k hóa mã K quy định áp dụng là 256 bit. Độ dài khóa được biểu diễn bằng một số Nk = 8 thể hiện số lượng các từ 32 bit (số cột) của Khóa mã. Số vòng trong quá trình thực thi thuật toán AES (được ký hiệu là Nr) với khóa độ dài 256 bit là Nr = 14.

Quy chuẩn này quy định cụ thể các giá trị được phép dùng cho độ dài khóa (Nk), kích cỡ khối (Nb) và số lượng vòng lặp (Nr) như Bảng 1.

Bảng 1: Các tổ hợp Khóa – Khối – Vòng

2.2.2.1. Phép mã hóa/giải mã AES

Đối với cả hai Phép mã hóa và Phép giải mã, thuật toán AES sử dụng hàm vòng bao gồm bốn phép biến đổi khác nhau trên byte:

1) Phép thay thế byte sử dụng bảng thay thế (S-box).

2) Dịch hàng của mảng Trạng thái bằng các offset khác nhau.

3) Trộn dữ liệu trong mỗi cột của mảng Trạng thái.

4) Bổ sung khóa vòng vào Trạng thái.

2.2.2.1.1. Phép mã hóa AES

Thuật toán AES gồm một dãy các phép toán được thực hiện trên mảng hai chiều của các byte, được gọi là Trạng thái. Trạng thái gồm bốn dòng byte, mỗi dòng chứa 4 byte. Trong mảng Trạng thái được ký hiệu bằng s, mỗi byte riêng biệt có hai chỉ số với số dòng r với 0 ≤ r < 4=”” và=”” số=”” cột=””>c, với 0 ≤ c < 4.=”” trạng=”” thái=”” được=”” ký=”” hiệu=”” là=””>S = (s_r,c).

Khi bắt đầu quá trình mã hóa, 16 byte của Trạng thái được khởi tạo với p_i byte bản rõ, tính từ trên xuống dưới và từ trái sang phải và được minh họa trên Hình 3.

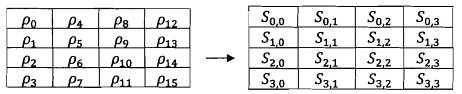
Hình 3: Khởi đầu Trạng thái

Sau khi cộng khóa vòng ban đầu, Trạng thái được biến đổi bằng cách thực thi hàm vòng Nr lần, với vòng cuối khác một ít với Nr – 1 vòng đầu. Nội dung cuối cùng của Trạng thái chính là bản mã đầu ra.

Phép mã hóa đầy đủ có thể được mô tả như sau:

(1) S = AddRoundKey(P,W₀)

(2) For i = 1 to Nr – 1

          S = SubBytes (S)

          S = ShiftRows(S)

          S = MixColumns(S)

          S = AddRoundKey(S, W_i)

(3) S = SubBytes (S),S = ShiftRows(S)

(4) C = AddRoundKey (S, W_Nr)

Các phép biến đổi riêng biệt SubBytes(), ShiftRows(), MixColumns(), AddRoundkey() xử lí Trạng thái và được mô tả tại Phụ lục B. Tất cả Nr vòng đều giống nhau, trừ vòng cuối cùng không chứa phép biến đổi MixColumns(). Trong phép toán ở trên, mảng W_i chứa các khóa vòng được mô tả tại Điều 2.2.2.2.

2.2.2.1.2. Phép giải mã AES

Tất cả các phép biến đổi sử dụng trong các phép mã hóa đều khả nghịch. Khi thực thi phép giải mã, dãy các phép biến đổi được sử dụng trong phép mã hóa vẫn được duy trì, nhưng thay bằng các phép biến đổi ngược như sau.

Phép giải mã đầy đủ có thể mô tả như sau:

(1) S = AddRoundKey (C,W_Nr)

(2) for i = Nr – 1 down to 1

          S = ShiftRows^-1(S)

          S = SubBytes^–1(S)

          S = AddRoundKey(S,W_i)

          S = MixColumns^-1(S)

(3) S = ShiftRows^–1(S)

     S = SubBytes^–1(S)

(4) P = AddRoundKey(S, W₀)

Các phép biến đổi SubBytes^–1(),ShiftRows^-1(),MixColumns^-1() thực hiện xử lí Trạng thái. Tất cả Nr vòng đều giống nhau, trừ vòng cuối không chứa phép biến đổi MixColumns^-1().

Các phép biến đổi SubBytes^-1(),ShiftRows^-1(),MixColumns^-1() thực hiện xử lí Trạng thái và được mô tả tại Phụ lục B. Tất cả Nr vòng đều giống nhau, trừ vòng cuối không chứa phép biến đổi MixColumns^-1(). Việc tính các khóa vòng W_i được mô tả tại Điều 2.2.2.2.

2.2.2.1.3. Quy định về S-Box và S-Box nghịch đảo trong AES

a) S-Box

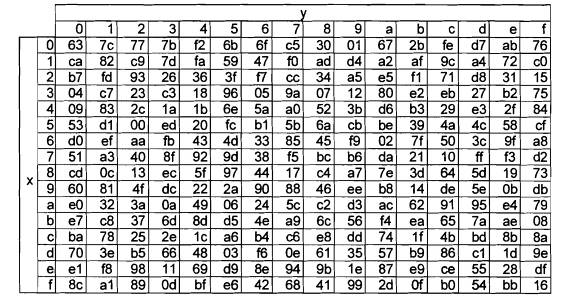
Bảng 2: S-Box: các giá trị thay thế cho byte {xy} (theo dạng thập lục phân)

b) S-Box nghịch đảo

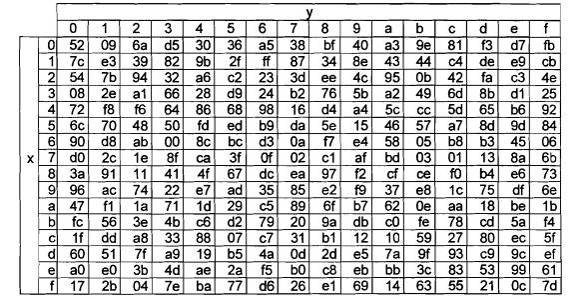
Bảng 3: S-Box nghịch: thay thế các giá trị theo byte {xy} (dạng thập lục phân)

2.2.2.2. Chu trình khóa

Thuật toán AES nhận khóa mật mã K và thực hiện thủ tục mở rộng khóa để tạo ra lược đồ khóa. Việc mở rộng khóa tạo ra tổng cộng 4(Nr + 1) từ: Thuật toán đòi hỏi tập khởi đầu gồm 4 từ, và mỗi vòng Nr vòng đòi hỏi 4 từ dữ liệu khóa. Lược đồ khóa nhận được là một mảng tuyến tính gồm các từ 4-byte, ký hiệu là w_j, với j nằm trong khoảng 0 ≤ j <>Nr + 1).

Phép mở rộng khóa đầy đủ cho AES-256 có thể được mô tả như sau:

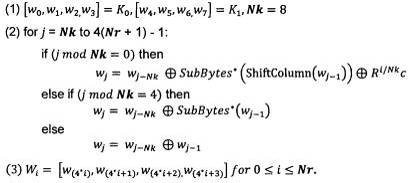
Trong phép toán trên K₀ và K₁ biểu thị hai nửa của khóa mật mã K 256-bit.

2.2.2.3. Chế độ hoạt động của AES

Các chế độ hoạt động của AES được quy định tại Mục 2.3 của Quy chuẩn này.

2.2.2.4. Khóa

Độ dài khóa sử dụng trong mã khối AES được quy định

Độ dài khối	Tên thuật toán	Độ dài khóa quy định áp dụng
128 bit	AES	Không nhỏ hơn 256 bit

2.2.3. Camellia

Trong Quy chuẩn này thuật toán mã đối xứng Camellia xử lí các khối 128 bit, sử dụng khóa mật mã độ dài không nhỏ hơn 256 bit.

2.2.3.1. Phép mã hóa/giải mã Camellia

2.2.3.1.1. Phép mã hóa Camellia

Quá trình mã hóa với khóa 256-bit làm việc trên 24 vòng, được chỉ ra trên Hình 4. Phép biến đổi khối 128 bit P vào khối 128-bit C được định nghĩa như sau (L và R là các biến độ dài 64 bit, kw, k và kl là các khóa vòng 64 bit):

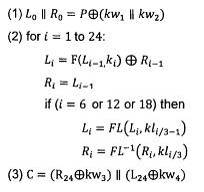
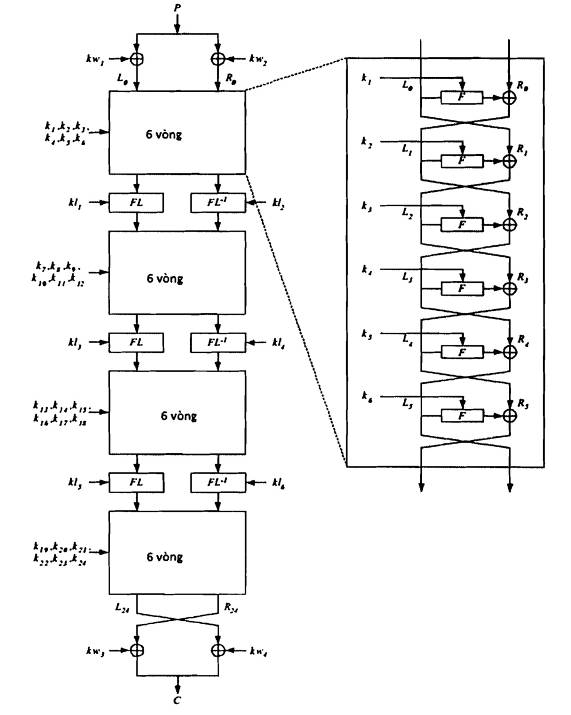
Hình 4: Thủ tục mã hóa Camellia cho khóa 256 bit

2.2.3.1.2. Phép giải mã Camellia

Quá trình giải mã cho khóa 256 bit được chỉ ra trên Hình 5, và là như nhau trong phép mã hóa, chỉ khác là vị trí và thứ tự các khóa vòng được đảo lại.

Phép giải mã được xác định như sau:

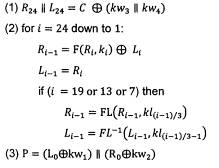
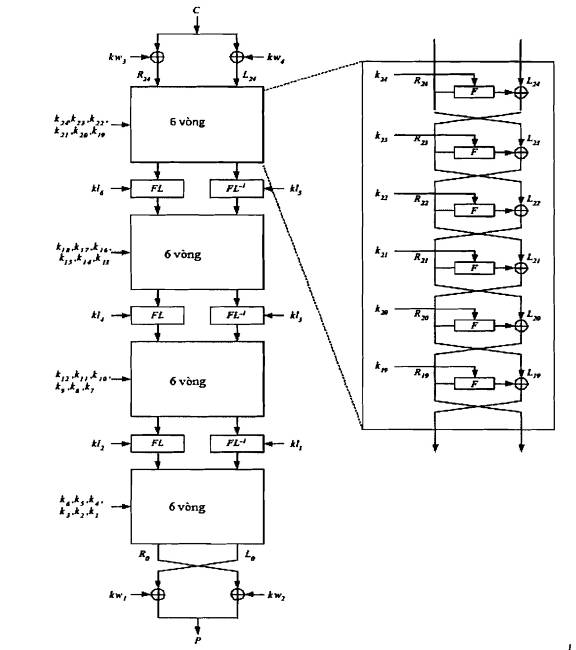
Hình 5: Thủ tục giải mã Camellia cho 256 bit

2.2.3.1.3. F-hàm

F-hàm được chỉ ra trên Hình 8. F-hàm bao gồm phép toán cộng bit XOR, tiếp đó áp dụng tám S-box song song kích thước 8×8 bit, tiếp theo tầng khuếch tán (P-hàm). x_j,y_j,z_j,z’_j là các biến, mỗi biến 8 bit; các biến L_i, k_i, L’_i là các biến 64 bit. Đầu vào 64 bit L_i trước hết được cộng XOR với khóa vòng 64-bit k_i, sau đó được chia thành 8 đoạn 8-bit y_j như sau:

y₁ || y₂ || y₃ || y₄ || y₅ || y₆ || y₇ || y₈ || = L_iÅk_i

ở đây,

L_i = x₁ || x₂ || x₃ || x₄ || x₅ || x₆ || x₇ || x₈

Mỗi y_j sau đó được đi qua S-box kích thước 8×8 bit s_t để đưa ra 8 phân đoạn độ dài 8 bit z_j, ở đây

8 phân đoạn 8 bit z_j được tác động bởi P-hàm, là lớp khuếch tán cho ra 8 phân đoạn 8-bit z’_j, trong đó

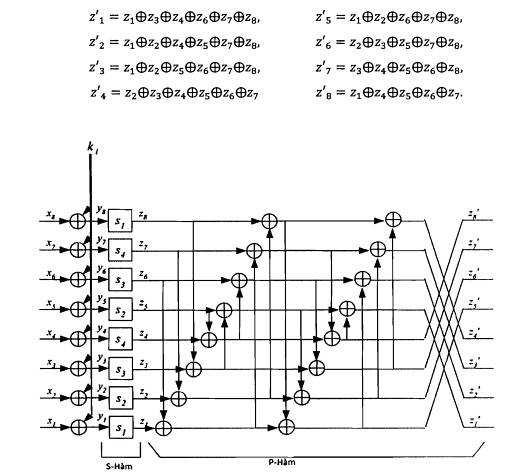
Hình 6: F-hàm

P-hàm có thể được biểu diễn cách khác, dưới dạng véc tơ ma trận như sau:

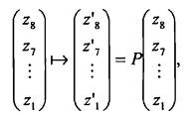
ở đây:

Sau đó đầu ra 64-bit của F-hàm L’_i được thiết lập bằng cách ghép các biến 8-bit z’_j:

2.2.3.2. Chu trình khóa

Với quy định khóa có độ dài 256 bit, khóa K là khóa 128-bit K_L và khóa 128-bit K_R. Như vậy,

K = K_L || K_R

Lược đồ tạo khóa sử dụng F-hàm của mô-đun mã hóa, và là giống nhau cho cả phép mã hóa và giải mã. Khóa K được mã bằng các phương tiện của F-hàm, sử dụng các hằng của lược đồ tạo khóa, ở đây các hằng Σ_i, được xác định như những giá trị liên tục biểu diễn trong hệ Hexa của căn bậc hai số nguyên tố thứ i. Tiếp đó các khóa vòng được tạo, một phần từ những giá trị được dịch vòng của khóa K (K = K_L II K_R) và phần còn lại từ các giá trị được dịch vòng của các khóa “được mã hóa” K_A và K_B (ở đây K_A, K_B có độ dài 128 bit).

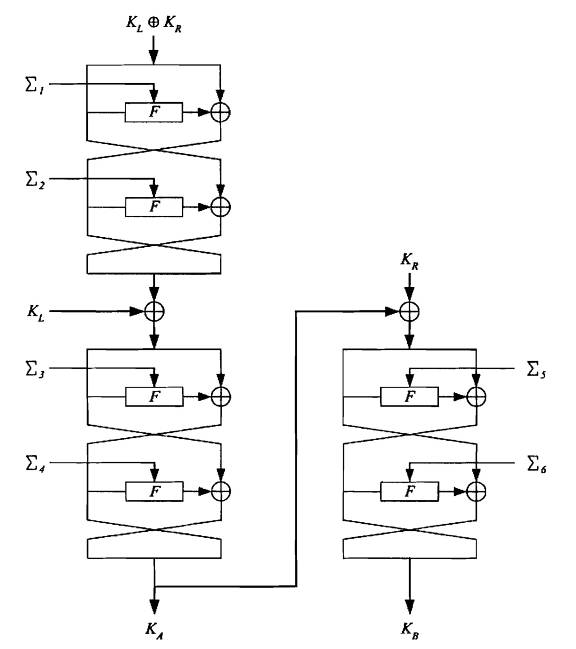
Hình 7: Phần chính của lược đồ khóa

Đối với khóa 256-bit, đầu ra của phần chính của lược đồ tạo khóa là khóa con 128 bit K_A và khóa con 128-bit K_B. Lược đồ tạo khóa bao gồm ba phép toán 2-vòng. Mỗi phép toán 2 vòng được “khóa hóa” bằng một cặp hằng Σ_i.

Đầu vào 128-bit của phép toán 2-vòng thứ nhất nằm bên trái của Hình 9 là K_LÅK_R và phép toán này được “khóa hóa” bởi hai hằng 64-bit Σ₁ và Σ₂. Tiếp đó đầu ra 128-bit từ phép toán 2-vòng thứ nhất được cộng bit XOR với K_L trước khi là đầu vào của phép toán 2-vòng thứ hai ở bên trái Hình 9. Phép toán 2-vòng thứ hai này được “khóa hóa” bởi các hằng 64 bit là Σ₃ và Σ₄. Đầu ra 128-bit của phép toán 2-vòng thứ hai là K_A, sau đó K_A lại được XOR với khóa con 128-bit K_R trước khi kết quả thu được làm đầu vào của phép toán 2-vòng thứ ba được chỉ ra ở phía phải của Hình 9. Phép toán 2-vòng thứ ba này được “khóa hóa” bởi hai hằng 64 bit là Σ₅ và Σ₆. Đầu ra 128 bit của phép toán 2-vòng thứ ba này là K_B.

Phép toán lập lược đồ tạo khóa đầy đủ được mô tả như sau (K_a, K_A và K_B có độ dài 128 bit):

(1) K_a = 2RoundFeistel(K_LÅK_R, Σ₁,Σ₂)

(2) K_A = 2RoundFeistel(K_aÅK_L, Σ₃,Σ₄)

(3) K_B = 2RoundFeistel(K_AÅK_R, Σ₅,Σ₆) (chỉ dùng cho khóa 192/256 bit)

ở đây đầu vào 128-bit cho 2RoundFeistel được tách thành hai phần 64-bit L₀ || R₀, đầu ra 128-bit từ 2RoundFeistel cũng được tách thành hai phần 64 bit L₂ || R₂ và cả hai đầu vào “khóa vòng” 64-bit của 2RoundFeistel là Σ_i và Σ_i+1.

2RoundFeistel được mô tả như sau:

(1) với j = 0,1:

          L_j+1 = F(L_j, Σ_i+j)ÅR_j

         R_j+1 = R_j

Các hằng của lược đồ khóa 64-bit được xác định trên Bảng 4

Bảng 4: Các hằng trong lược đồ khóa

Cuối cùng, các khóa vòng 64-bit, k, kw,và kl được dẫn xuất từ các khóa con 128-bit, K_L, K_R, K_A và K_B.

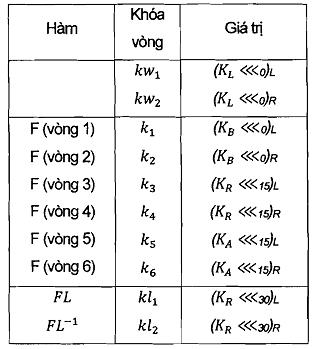
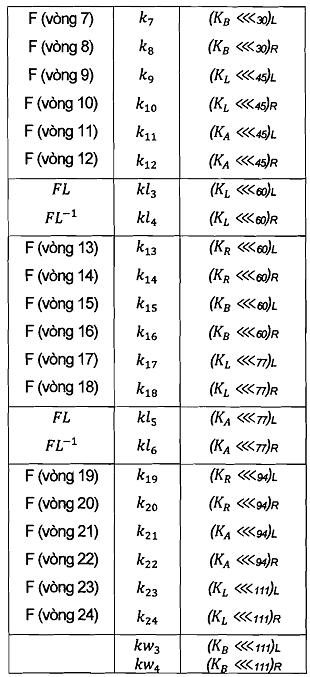
Bảng 5: Khóa vòng cho khóa bí mật 256 bit

2.2.3.3. Chế độ hoạt động của Camellia

Các chế độ hoạt động của Camellia được quy định tại Mục 2.3 của Quy chuẩn này.

2.2.3.4. Khóa

Độ dài khóa sử dụng trong mã khối Camellia được quy định

Độ dài khối	Tên thuật toán	Độ dài khóa quy định áp dụng
128 bit	Camellia	Không nhỏ hơn 256 bit

2.3. Chế độ hoạt động của mã khối

Mục này của Quy chuẩn sử dụng một số ký hiệu sau:

C	Khối bản mã
CTR	Giá trị đếm
i	Biến lặp
j	Kích thước của biến bản rõ/bản mã
K	Khóa mật mã
n	Độ dài khối bản mã/bản rõ đối với một mã khối
m	Số khối bản mã được lưu trữ
P	Khối bản rõ
q	Số các biến bản rõ/bản mã
r	Kích thước bộ đệm phản hồi
SV	Biến khởi đầu
X	Khối đầu vào mã khối
Y	Khối đầu ra mã khối

2.3.1. Chế độ xích liên kết khối mã CBC (Cipher Block Chaining)

Chế độ CBC được xác định bởi một tham số xen kẽ m > 0, số khối bản mã phải được lưu trữ trong khi xử lý trong chế độ này. Giá trị của m cần nhỏ (thông thường m = 1) và lớn nhất là 1024.

a) Các biến được sử dụng trong chế độ CBC:

1) Dãy q khối bản rõ có độ dài n bit P₁, P₂, …, P_q.

2) Khóa bí mật K.

3) Dãy các biến khởi đầu có độ dài n bit SV₁, SV, …,SV_m.

b) Các biến đầu ra là dãy q biến bản mã có độ dài n bit C₁, C₂,…, C_q

2.3.1.1. Phép mã hóa

Phép mã hóa của chế độ CBC như sau:

C_i = e_K(P_i ÅSV_i), 1 ≤ i ≤ min(m, q)

Nếu q > m, các khối bản rõ theo sau được mã hóa như sau:

C_i = e_K(P_i ÅC_i-m),m + 1 ≤ i ≤ q

CHÚ THÍCH: Tại bất kỳ thời điểm nào trong quá trình tính toán, giá trị của khối bản mã m gần nhất cần được lưu trữ.

2.3.1.2. Phép giải mã

Phép giải mã của chế độ CBC như sau:

P_i = d_K(C_i) Å SV_i, 1 ≤ i ≤ min(m, q)

Nếu q >m, các khối bản rõ theo sau được mã hóa như sau:

P_i = d_K(C_i) Å C_i-m, m+ 1 ≤ i ≤ q

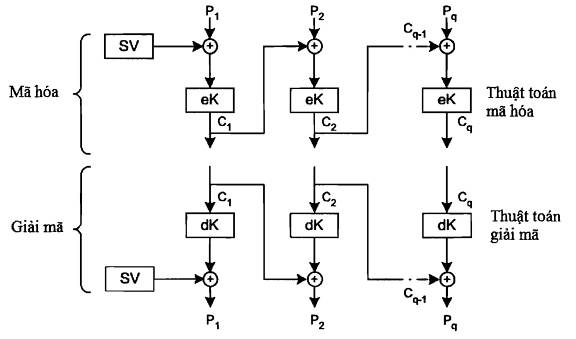
Hình 8: Chế độ xích liên kết khối mã với m = 1

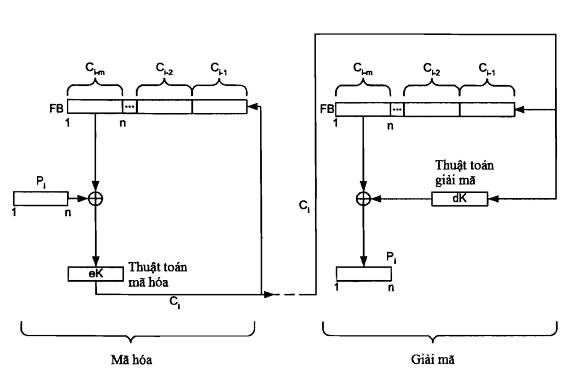
Hình 9: Chế độ xích liên kết khối mã

– Biến khởi đầu SV được sinh ngẫu nhiên, giữ bí mật và thông báo cho nhau.

– Yêu cầu về đệm (padding)

+ Nếu độ dài bản rõ không phải là bội số của n thì yêu cầu sử dụng phương pháp đệm (padding) sau để bổ sung bản rõ sao cho độ dài của bản rõ là bội số của n:

Thêm một bit 1 vào cuối bản rõ, tiếp sau là các bít 0 (có thể không cần) để được bản rõ có độ dài là bội số của n. Đây chính là phương pháp đệm 2 trong tiêu chuẩn ISO/IEC 9797-1 hoặc ISO/IEC 10118-1

2.3.2. Chế độ phản hồi mã CFB (Cipher FeedBack)

Chế độ CFB được xác định bởi 3 tham số:

– Kích thước của bộ đệm phản hồi, r, trong đó n ≤ r ≤ 1024n và r <>

– Kích thước của biến phản hồi, k, trong đó 1 ≤ K ≤ n

– Kích thước của biến bản rõ, j, trong đó 1 ≤ j ≤ k

Trong Quy chuẩn này thì giá trị của j và k bằng nhau.

Các biến được sử dụng trong chế độ CFB:

a) Các biến đầu vào

1) Dãy q biến bản rõ độ dài j bit P₁, P₂, …, P_q.

2) Khóa bí mật K.

3) Biến khởi đầu độ dài r bit.

b) Các kết quả trung gian:

1) Dãy q khối đầu vào của mã khối độ dài n bit X₁,X₂,…,X_q.

2) Dãy q khối đầu ra của mã khối độ dài n bit Y₁,Y₂,…,Y_q.

3) Dãy q biến độ dài j bit E₁,E₂,…,E_q.

4) Dãy q – 1 biến phản hồi độ dài k bit F₁,F₂,…,F_q-1.

5) dãy q nội dung bộ đệm phản hồi độ dài r bit FB₁,FB₂,…,FB_q.

c) Các biến đầu ra là dãy q biến bản mã độ dài j bit C₁,C₂,…,C_q. 

2.3.2.1. Phép mã hóa

Bộ đệm phản hồi FB được gán giá trị khởi đầu.

FB₁ = SV

Phép toán mã hóa mỗi biến bản rõ thực hiện trong 6 bước sau:

a) X_i = n~FB_i (Lựa chọn n bit tận cùng bên trái của FB).

b) Y_i = e_K(X_i) (Sử dụng mã khối).

c) E_i = j~Y_i (Lựa chọn j bit tận cùng bên trái của Y_i).

d) C_i = P_i Å E_i (Tạo biến bản mã).

e) F_i = I(k – j)|C_i (Tạo biến phản hồi).

f) FB_i+1 = S_k(FB_i|F_i) (Hàm dịch chuyển trên FB).

Các bước trên lặp với biến đếm i = 1,2,…,q, trong vòng lặp cuối dừng lại tại bước (d). j bit tận cùng bên trái của khối đầu ra Y của mã khối được sử dụng để mã hóa j-bit biến bản rõ theo phép cộng modulo 2. Các bit còn lại của Y được bỏ đi. Các bit biến bản rõ/bản mã có chỉ số từ 1 đến j.

Biến bản mã được tăng thêm bằng cách đặt k – j bit trong vị trí bit tận cùng bên trái của mình để tạo biến phản hồi F độ dài k-bit. Sau đó các bit của bộ đệm phản hồi FB được dịch trái đi k vị trí và F được thêm vào vị trí k tận cùng bên phải để tạo ra giá trị mới của bộ đệm phản hồi FB. Trong phép toán dịch, k bit tận cùng bên trái của FB được bỏ đi. n bit tận cùng bên trái mới của FB được sử dụng như là đầu vào tiếp theo của X trong quá trình mã hóa.

2.3.2.2. Phép giải mã

Bộ đệm phản hồi FB được gán giá trị khởi đầu.

FB₁ = SV

Phép toán giải mã mỗi biến bản mã thực hiện trong 6 bước sau:

a) X_i = n~FB_i (Lựa chọn n bit tận cùng bên trái của FB).

b) Y_i = e_K(X_i) (Sử dụng mã khối).

c) E_i = j~Y_i (Lựa chọn j bit tận cùng bên trái của Y_i).

d) P_i = C_i Å E_i (Tạo biến bản rõ).

e) F_i = l(k – j)|C_i (Tạo biến phản hồi).

f) FB_i+1 = S_k(FB_i|F_i) (Hàm dịch chuyển trên FB).

Các bước trên lặp với biến đếm i = 1,2,…,q, trong vòng lặp cuối dừng lại tại bước (d). j bit tận cùng bên trái của khối đầu ra Y của mã khối được sử dụng để giải mã biến bản mã theo phép cộng modulo 2. Các bit còn lại của Y được bỏ đi. Các bit biến bản rõ/bản mã có chỉ số từ 1 đến j.

Biến bản mã được tăng thêm bằng cách đặt k – j bit trong vị trí bit tận cùng bên trái của mình để tạo biến phản hồi F độ dài k-bit. Sau đó các bit của bộ đệm phản hồi FB được dịch trái đi k vị trí và F được thêm vào vị trí k tận cùng bên phải để tạo ra giá trị mới của bộ đệm phản hồi FB. Trong phép toán dịch, k bit tận cùng bên trái của FB được bỏ đi. n bit tận cùng bên trái mới của FB được sử dụng như là đầu vào tiếp theo của X trong quá trình mã hóa.

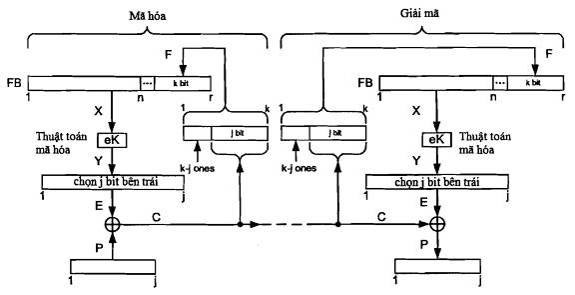
Hình 10: Chế độ phản hồi mã CFB

2.3.3. Chế độ phản hồi đầu ra OFB (Output Feedback):

Chế độ OFB được xác định bằng một tham số j là kích thước biến bản rõ với 1 ≤ j ≤ n.

Các biến được sử dụng trong chế độ OFB là:

a) Các biến đầu vào:

1) Dãy q biến bản rõ độ dài j bit P₁, P₂, ... P_q.

2) Khóa bí mật K.

3) Biến khởi đầu độ dài n bit.

b) Các kết quả trung gian:

1) Dãy q khối đầu vào của mã khối độ dài n bit X₁, X₂,…, X_q.

2) Dãy q khối đầu ra của mã khối độ dài n bit Y₁, Y₂,…, Y_q.

3) Dãy q biến độ dài j bit E₁, E₂,…, E_q.

c) Các biến đầu ra là dãy q biến bản mã độ dài j bit C₁, C₂,…, C_q.

2.3.3.1. Phép mã hóa

Khối đầu vào X được gán giá trị khởi đầu

X₁ = SV

Phép toán mã hóa mỗi biến bản rõ thực hiện trong 4 bước sau:

a) Y_i = e_k(X_i) (Sử dụng mã khối).

b) E_i = j~Y_i (Chọn j bit tận cùng bên trái).

c) C_i = P_i Å E_i (Tạo biến bản mã).

d) X_i+1 = Y_i (Phép toán phản hồi).

Các bước trên lặp với biến đếm i = 1,2,…,q, trong vòng lặp cuối dừng lại tại bước (c). Các biến bản mã và bản rõ có các bit với chỉ số từ 1 đến j.

Kết quả của mỗi lần sử dụng mã khối là Y_i và được đưa trở lại thành giá trị tiếp theo của X, đặt là X_i+1. j bit tận cùng bên trái của Y_i được sử dụng để mã hóa biến đầu vào.

2.3.3.2. Phép giải mã

Khối đầu vào X được gán giá trị khởi đầu

X₁ = SV

Phép toán giải mã mỗi biến bản mã thực hiện trong 4 bước sau:

a) Y_i = e_k(X_i) (Sử dụng mã khối).

b) E_i = j~Y_i (Chọn j bit tận cùng bên trái).

c) C_i = P_i Å E_i (Tạo biến bản mã).

d) X_i+1 = Y_i (Phép toán phản hồi).

Các bước trên lặp với biến đếm i = 1,2,…,q, trong vòng lặp cuối dừng lại tại bước (c). Các biến bản mã và bản rõ có các bit với chỉ số từ 1 đến j.

Kết quả của mỗi lần sử dụng mã khối là Y_i và được đưa trở lại thành giá trị tiếp theo của X, đặt là X_i+1. j bit tận cùng bên trái của Y_i được sử dụng để giải mã biến đầu vào.

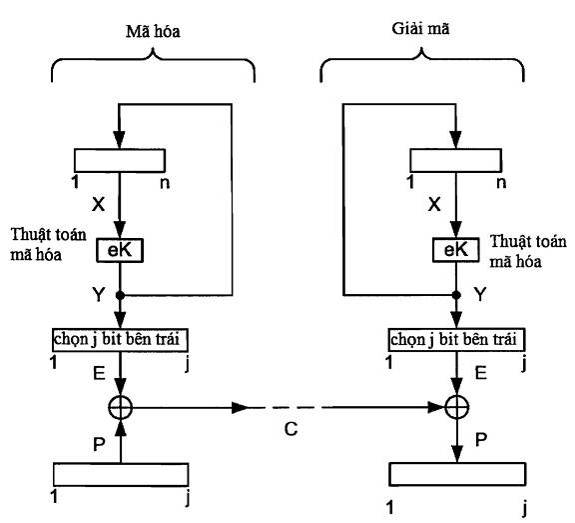
Hình 11: Chế độ phản hồi đầu ra OFB

2.3.4. Chế độ đếm CTR (Counter)

Chế độ CTR được xác định bằng một tham số j trong đó 1 ≤ j ≤ n.

Các biến được sử dụng trong chế độ CTR là:

a) Các biến đầu vào:

1) Dãy q biến bản rõ độ dài j bit P₁, P₂, …, P_q, mỗi biến có độ dài j bit.

2) Khóa bí mật K.

3) Biến khởi đầu SV có độ dài n bit.

b) Các kết quả trung gian:

1) Dãy q khối đầu vào của mã khối độ dài n bit CTR₁,CTR₂,…,CTR_q.

2) Dãy q khối đầu ra của mã khối độ dài n bit Y₁,Y₂,…,Y_q.

3) Dãy q biến độ dài j bit E₁,E₂,…,E_q.

c) Các biến đầu ra là dãy q biến bản mã độ dài j bit C₁,C₂,…,C_q. 

2.3.4.1. Phép mã hóa

CTR được gán giá trị khởi đầu

CTR₁ = SV

Các phép toán để mã hóa mỗi biến bản rõ theo 4 bước sau:

a) Y_i = e_K(CTR_i) (Sử dụng mã khối).

b) E_i = j~Y_i (Chọn j bit tận cùng bên trái của Y_i).

c) C_i = P_i Å E_i (Tạo ra biến bản mã).

d) CTR_i+1 = (CTR_i + 1)mod 2ⁿ (Tạo ra giá trị đếm mới CTR).

Các bước trên lặp với biến đếm i = 1,2,…,q, trong vòng lặp cuối dừng lại tại bước (c). Các biến bản mã và bản rõ có các bit có chỉ số từ 1 đến j.

Giá trị đếm được mã hóa để đưa ra khối đầu ra Y_i và j bit tận cùng bên trái của khối đầu ra Y_i được sử dụng để mã hóa giá trị đầu vào. CTR sau đó được tăng 1 (modulo 2ⁿ) để tạo ra giá trị đếm mới.

2.3.4.2. Phép giải mã

CTR được gán giá trị khởi đầu

CTR₁ = SV

Các phép toán để giải mã mỗi biến bản rõ theo 4 bước sau:

a) Y_i = e_K(CTR_i) (Sử dụng mã khối).

b) E_i = j~Y_i (Chọn j bit tận cùng bên trái của Y_i).

c) P_i = C_i Å E_i (Tạo biến bản rõ).

d) CTR_i+1 = (CTR_i + 1)mod 2ⁿ (Tạo ra giá trị đếm mới CTR).

Các bước trên lặp với biến đếm i = 1,2,…,q, trong vòng lặp cuối dừng lại tại bước (c). Các biến bản mã và bản rõ có các bit có chỉ số từ 1 đến j.

Giá trị đếm được mã hóa để đưa ra khối đầu ra Y_i và j bit tận cùng bên trái của khối đầu ra Y_i được sử dụng để mã hóa giá trị đầu vào. CTR sau đó được tăng 1 (modulo 2ⁿ) để tạo ra giá trị đếm mới.

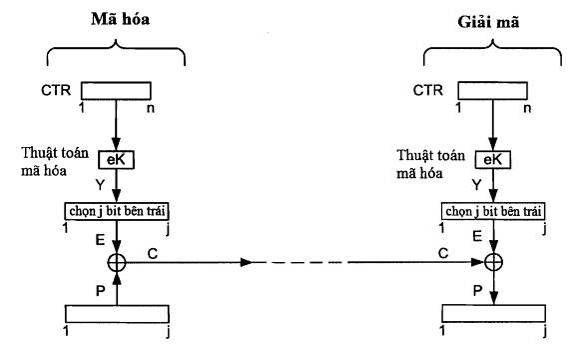
Hình 12: Chế độ đếm CTR

2.4. Mã dòng

Mã dòng là mã thực hiện biến đổi từng bit dữ liệu của bản rõ sang bản mã sử dụng khóa độ dài k  bit. Quy chuẩn này quy định sử dụng các mã khối được quy định tại Mục 2.2 sử dụng chế độ CFB, OFB hoặc CTR để thực hiện chức năng mã dòng.

3. QUY ĐỊNH VỀ QUẢN LÝ

3.1. Các mức giới hạn của đặc tính kỹ thuật mật mã và yêu cầu quản lý của các thuật toán mật mã để mã hóa dữ liệu nêu tại Quy chuẩn này là các chỉ tiêu chất lượng phục vụ được quản lý theo quy định về quản lý chất lượng sản phẩm, dịch vụ mật mã dân sự được quy định tại Luật An toàn thông tin mạng ngày 19 tháng 11 năm 2015.

3.2. Hoạt động kiểm tra chất lượng sản phẩm, dịch vụ mật mã được cơ quan quản lý nhà nước có thẩm quyền tiến hành định kỳ hàng năm hoặc đột xuất.

4. TRÁCH NHIỆM CỦA TỔ CHỨC, CÁ NHÂN

4.1. Các tổ chức tín dụng (trừ quỹ tín dụng nhân dân cơ sở có tài sản dưới 10 tỷ, tổ chức tài chính vi mô) sử dụng sản phẩm, dịch vụ mật mã dân sự có trách nhiệm đảm bảo tuân thủ Quy chuẩn này và chịu sự kiểm tra của cơ quan quản lý nhà nước theo quy định.

4.2. Doanh nghiệp cung cấp sản phẩm, dịch vụ mật mã dân sự cho các tổ chức tín dụng (trừ quỹ tín dụng nhân dân cơ sở có tài sản dưới 10 tỷ, tổ chức tài chính vi mô) có trách nhiệm thực hiện công bố hợp quy sản phẩm, dịch vụ mật mã dân sự phù hợp với Quy chuẩn này. Việc công bố hợp quy thực hiện theo Thông tư số 28/2012/TT-BKHCN ngày 12 tháng 12 năm 2012 của Bộ Khoa học và Công nghệ.

4.3. Cục Quản lý mật mã dân sự và Kiểm định sản phẩm mật mã – Ban Cơ yếu Chính phủ có trách nhiệm tiếp nhận đăng ký công bố hợp quy, thực hiện quản lý, hướng dẫn và kiểm tra việc công bố hợp quy.

5. TỔ CHỨC THỰC HIỆN

5.1. Cục Quản lý mật mã dân sự và Kiểm định sản phẩm mật mã – Ban Cơ yếu Chính phủ có trách nhiệm hướng dẫn, tổ chức triển khai quản lý kỹ thuật mật mã của thuật toán mã hóa dữ liệu theo Quy chuẩn này.

5.2. Trong trường hợp các quy định nêu tại Quy chuẩn kỹ thuật quốc gia này có sự thay đổi, bổ sung hoặc được thay thế thì thực hiện theo quy định tại văn bản mới./.

 

PHỤ LỤC A

(Quy định)

Mô tả DES

A.1. Mở đầu

Thuật toán DES là mã khối đối xứng có thể xử lí các khối dữ liệu 64 bit, sử dụng khóa bí mật độ dài 64 bit. Mỗi bit thứ tám của khóa mật mã thường được sử dụng để kiểm tra tính chẵn lẻ và được bỏ qua.

A.2. Phép mã hóa DES

Phép mã hóa được chỉ ra trên Hình A.1

Bản rõ 64-bit trước hết được biến đổi qua hoán vị ban đầu IP. Sau đó khối được chia thành hai nửa L₀ và R₀, mỗi nửa gồm 32 bit. Tiếp đó thực hiện 16 vòng biến đổi giống nhau được gọi là hàm f, trong đó dữ liệu được kết hợp với khóa. Trong mỗi vòng, nửa phải là đầu vào của hàm f được khóa hóa, hàm này nhận đầu vào 32 bit và khóa con 48 bit K_i và cho đầu ra 32-bit. Đầu ra này tiếp đó được XOR với nửa trái để tạo ra nửa trái mới đã được biến đổi. Tại phần cuối của mỗi vòng, trừ vòng cuối cùng, hai nửa trái và phải đổi chỗ cho nhau để tạo ra L_i và R_i tương ứng. Sau khi thực hiện vòng cuối cùng, hai nửa trái và phải được ghép lại với nhau và khối 64-bit nhận được lại được biến đổi qua phép hoán vị cuối IP^–1 là hoán vị nghịch đảo của hoán vị ban đầu IP. Đầu ra là bản mã 64 bit.

Phép mã hóa được xác định như sau (P và C là dữ liệu, K_i là khóa).

(1) IP(P) = L₀ || R₀

(2) Với i = 1,2…,16:

            L_i = R_i–1

            R_i = L_i-1 Åf(R_i-1,K_i)

(3) C = IP^–1(R₁₆ || L₁₆)

A.3. Phép giải mã DES

Phép giải mã cũng giống như phép mã hóa. Sự khác nhau chỉ ở chỗ, các khóa con K_i được sử dụng theo thứ tự ngược lại.

A.4. Các hàm DES

A.4.1. Phép hoán vị ban đầu IP

Phép hóa vị ban đầu IP được chỉ ra tại Bảng A.1. Hoán vị này nhận đầu vào 64-bit và cho đầu ra 64-bit, theo đó bit thứ nhất được hoán vị thành bit thứ 58, bit thứ hai thành bit thứ 50.v.v, bit cuối cùng thành bit thứ 7.

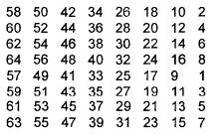
Bảng A.1 – Hoán vị khởi tạo

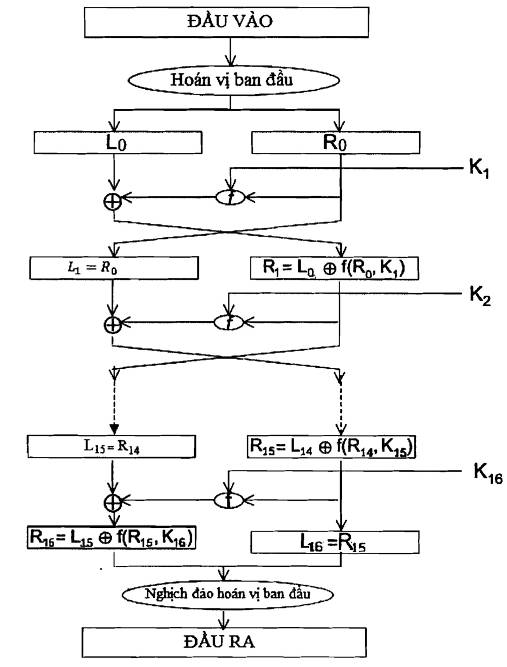
Hình A.1 – Thủ tục mã hóa

A.4.2. Hoán vị nghịch đảo IP^-1

Hoán vị nghịch đảo IP^-1 được chỉ ra trên Bảng A.2, nhận đầu vào 64-bit và cho đầu ra 64- bit. Đầu ra của Thuật toán nhận bit thứ 40 của khối đầu ra trước đó làm bit thứ nhất, bit thứ 8 làm bit thứ hai.v.v và bit thứ 25 của khối đầu ra trước đó làm bit cuối cùng.

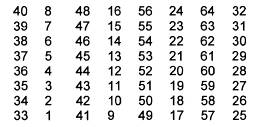
Bảng A.2 – Hoán vị nghịch đảo IP^-1

A.4.3. Hàm f

Hàm f được chỉ ra trên Hình A.2

Hàm f nhận đầu vào 32 bit R và mở rộng thành R’ có độ dài 48-bit bằng cách sử dụng phép hoán vị mở rộng E. Sau đó 48-bit R’ được XOR với khóa con 48-bit K, thu được dữ liệu 48- bit, dữ liệu này được viết thành 8 khối, mỗi khối 6-bit, bằng cách chọn các bit đầu vào của nó theo một thứ tự được qui định trên bảng. Các hàm được chọn duy nhất đó được gọi là các S – box, S₁, S₂,…,S₈ nhận đầu vào là các khối 6-bit r_i và cho đầu ra là các khối 4-bit S_i(r_i). Hàm hoán vị P cho đầu ra 32-bit R”” từ đầu vào 32-bit R”” bằng cách hoán vị các bit của khối đầu vào. R”” là đầu ra của hàm f.

Hàm f do đó được xác định như sau (P và C là dữ liệu, K_i là khóa )

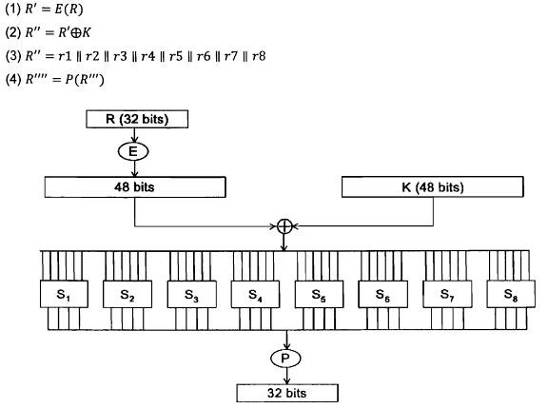
Hình A.2 – Tính f(R,K)

A.4.4. Hoán vị mở rộng E

Hoán vị mở rộng E được chỉ ra trên Bảng A.3. Hoán vị E nhận đầu vào 32- bit và cho đầu ra 48-bit. Ba bit đầu tiên của E là các bit ở các vị trí 32, 1 và 2, hai bit cuối ở các vị trí 32 và 1.

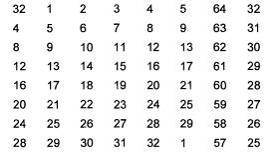
Bảng A.3 – Hoán vị mở rộng E

A.4.5. Hoán vị P

Hoán vị P được chỉ ra trên Bảng A.4. Hoán vị P nhận đầu vào 32-bit và cho đầu ra 32-bit. Đầu ra P(L) của hàm P được xác định bởi Bảng A.4, thu được từ đầu vào L bằng cách lấy bit thứ 16 của L làm bit thứ nhất của P(L), bit thứ bảy làm bit thứ hai của P(L),v.v và bit thứ 25 của L làm bit thứ 32 của P(L).

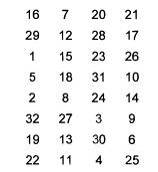
Bảng A.4 – Hoán vị P

A.4.6. S-box

S-box được chỉ ra trên Bảng A.5. Mỗi S-box có 6- bit đầu vào và 4-bit đầu ra.

Nếu S₁ là hàm được xác định trên bảng và B là khối 6-bit, thì S₁(B) được xác định như sau: các bit đầu tiên và cuối cùng của B được biểu diễn theo cơ số 2 là một số nằm trong khoảng từ 0 đến 3. Giả sử số đó là i. Bốn bit giữa của B được biểu diễn theo cơ số 2 là số nằm trong khoảng từ 0 đến 15. Giả sử số đó là j. Trên bảng đó là số nằm trên hàng thứ i và cột thứ j. Đó là số nằm trong khoảng từ 0 đến 15, và được biểu diễn duy nhất bởi khối 4-bit. Khối này là đầu ra S₁(B) của S₁ ứng với đầu vào B. Ví dụ, với đầu vào 011011, hàng được biểu diễn bởi 01 là hàng 1, cột được xác định bởi 1101 là cột 13. Nằm trên giao của hàng 1 và cột 13 là số 5, do đó đầu ra là 0101.

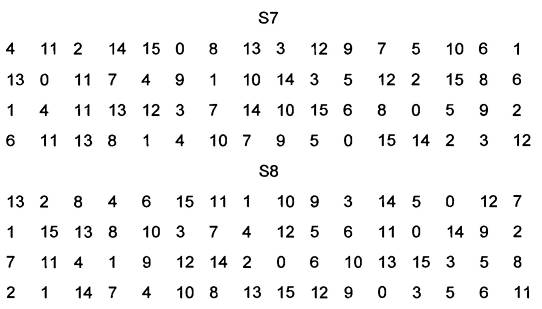
Bảng A.5 – Các S-box

A.5. Lược đồ tạo khóa DES

Phần lược đồ khóa DES được chỉ ra trên Hình A.3. Lược đồ này nhận khóa 64-bit khóa KEY và cho ra 16 khóa con 48-bit K₁, K₂,……, K₁₆.

Trong đó K_n, với 1 ≤ n ≤ 16 là khối 48-bit trong bước (2) của thuật toán. Bởi vậy để mô tả KS chỉ cần mô tả việc tính toán của K_n từ KEY với n = 1, 2…, 16. Việc tính toán này được mô tả trên Hình A.3. Do đó để xác định đầy đủ KS, chỉ cần mô tả hai lựa chọn hoán vị, cũng giống như lược đồ chuyển dịch sang trái. Một bit trong byte 8-bit của KEY có thể được khởi động để phát hiện lỗi trong tạo khóa, phân phối và lưu trữ khóa. Các bit 8,16,…, 64 được sử dụng để bảo đảm là mỗi byte có tính chất lẻ. Lựa chọn hoán vị 1 được xác định bởi Bảng A.6

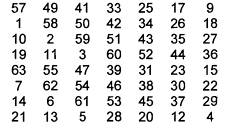
Bảng A.6 – Hoán vị khóa PC-1

Bảng trên được chia thành hai phần, phần thứ nhất xác định cách chọn các bit trong C₀, phần thứ hai xác định cách chọn các bit trong D₀. Các bit của KEY được đánh số từ 1 đến 64. Các bit trong C₀ tương ứng là 57, 49, 41,…, 44 và 36 của KEY, còn các bit trong D₀ là các bit 63, 55, 47,..,12 và 4 của KEY. Với C₀ và D₀ đã xác định, có thể xác định được C_n và D_n từ C_n-1 và D_n-1, tương ứng với n = 1, 2,…, 16. Điều này đạt được bằng cách tuân thủ vào lược đồ phép dịch sang trái các khối riêng lẻ sau:

	Số lần lặp 1 2 3 4 5 6 7 8	Số lần dịch trái 1 1 2 2 2 2 2 2
	Số lần lặp 9 10 11 12 13 14 15 16	Số lần dịch trái 1 2 2 2 2 2 2 1

Bảng A.7 – Số các bit khóa được dịch chuyển của mỗi vòng

Ví dụ, C₃ và D₃ thu được từ C₂ và D₂ tương ứng bằng hai dịch chuyển sang trái, và C₁₆ và D₁₆ thu được từ C₁₅ và D₁₅ tương ứng bằng một lần dịch sang trái. Trong tất cả các trường hợp, việc dịch một lần sang trái được hiểu là dịch các bit sang trái một vị trí sao cho sau một lần dịch các bit ở 28 vị trí là các bit trước đó ở vị trí 2, 3,…, 28, 1. Việc chọn hoán vị 2 được xác định trên Bảng A.8

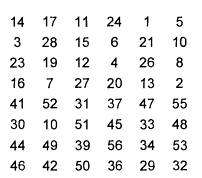
Bảng A.8 – Hoán vị nén PC-2

Bởi vậy bit thứ nhất của K_n là bit thứ 14 của C_nD_n, bit thứ hai là bit thứ 17.v.v, bit thứ 47 là bit thứ 29, bit thứ 48 là bit thứ 32.

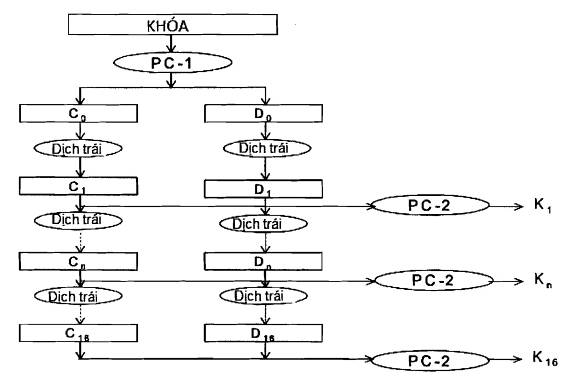
Hình A.3 – Tính toán lược đồ khóa

 

PHỤ LỤC B

(Quy định)

Các phép biến đổi của AES

B.1. Các phép biến đổi AES

B.1.1. Các phép biến đổi xác định cho AES

Thuật toán AES sử dụng các phép biến đổi SubBytes(), SubBytes^-1() ShiftRows(), ShiftRows^-1(), MixColumns(), MixColumns^-1(), AddRoundKey(), được mô tả dưới đây.

B.1.2. Phép biến đổi SubBytes()

Phép biến đổi SubBytes() thực hiện thay thế mỗi byte Trạng thái s_i,j bởi giá trị mới s’_ij, bằng cách sử dụng bảng thay thế (S-box) khả nghịch.

Hình B.1 minh họa tác động của phép biến đổi SubBytes() lên bảng Trạng thái

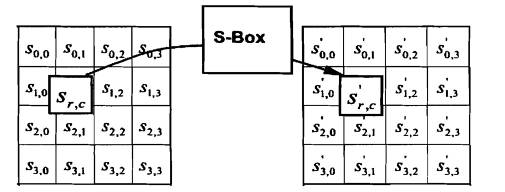
Hình B.1: SubBytes() áp dụng S-box cho từng byte của Trạng thái.

S-box được sử dụng trong phép biến đổi SubBytes() và được trình bày theo hệ Hexa trên Bảng B.1

Bảng B.1: Các S-box của AES

Ví dụ, nếu s_1,1 = {53} thì giá trị thay thế là giá trị nằm trên giao của hàng có chỉ số ‘5’ và cột có chỉ số ‘3’ của Bảng 5, điều này cho kết quả là s’_1,1 có giá trị {ed}.

B.1.3. Phép biến đổi SubBytes^-1()

SubBytes^-1() là phép biến đổi nghịch đảo của phép biến đổi SubBytes(), trong đó S-box nghịch đảo được áp dụng cho từng byte của Trạng thái. Điều này đạt được bằng cách áp dụng phép biến đổi nghịch đảo được mô tả tại Điều 5.2.4.2

S-box nghịch đảo được sử dụng trong phép biến đổi SubBytes^-1() được mô tả trong Bảng B.2.

Bảng B.2: S-box nghịch đảo AES

B.1.4. Phép biến đổi ShiftRows()

Trong phép biến đổi ShiftRows(), các byte ở ba dòng cuối của Trạng thái được dịch vòng lên một số lượng bytes khác nhau (offsets). Hàng thứ nhất, hàng 0 được giữ nguyên (không dịch chuyển).

Cụ thể, phép biến đổi ShiftRows() được thực hiện như sau:

S‘_r,c = S_{r (c+r)mod4} với 0 r < 4,=”” và=”” 0=””> c < 4,=”” ở=””> r là số thứ tự của hàng.

Theo đó các byte dịch sẽ chuyển sang trái (nghĩa là các giá trị thấp hơn của c trong một hàng cho trước), trong khi các byte phía trái ngoài cùng dịch vòng sang các vị trí phía phải ngoài cùng của hàng (tức là những giá trị cao hơn của c trong hàng cho trước).

Hình B.2 mô tả phép biến đổi ShiftRows(), trong đó các byte được dịch vòng sang trái.

B.1.5. Phép biến đổi ShiftRows^-1()

ShiftRows^-1() là phép nghịch đảo của phép biến đổi ShiftRows(). Các bytes trong ba dòng cuối của Trạng thái được dịch vòng lên một số lượng bytes khác nhau. Dòng thứ nhất, dòng 0 không dịch chuyển. Ba dòng dưới cùng được dịch vòng lên 4 – r bytes, ở đây r là số thứ tự vòng.

Cụ thể, phép biến đổi ShiftRows^-1() được thực hiện như sau:

S_r,(c+r)mod4 = S‘_r,c với 0 r < 4,=”” và=”” 0=””> c < 4.=””>

Hình B.3. mô tả phép biến đổi ShiftRows^-1()

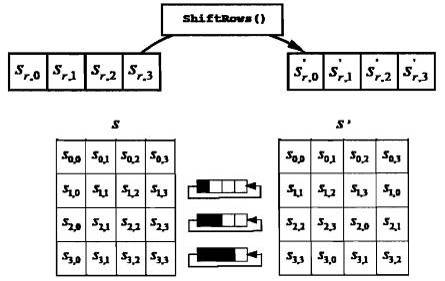
Hình B.2: ShiftRows() dịch vòng ba dòng cuối của Trạng thái

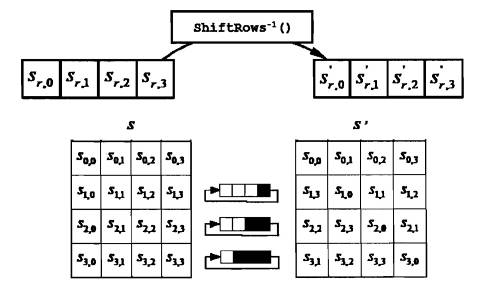
Hình B.3: ShiftRows^-1() dịch vòng ba dòng cuối của Trạng thái.

B.1.6. Phép biến đổi MixColumns()

Phép biến đổi MixColumns() thao tác trên Trạng thái, thay mỗi cột bằng cột khác. Các cột của Trạng thái được xem như những đa thức trên trường GF(2⁸) và được nhân modulo x⁴ + 1 với đa thức cố định a(x) cho trước, a(x) = {03}x³ + {01}x² + {01}x + {02}. Phép nhân này có thể viết dưới dạng phép nhân ma trận:

Kết quả của phép nhân trên là bốn byte trong cột được thay thế như sau:

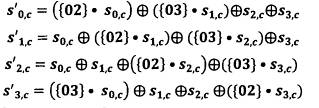
Toán tử Å trong các biểu thức trên biểu thì phép cộng trong trường GF(2⁸), với phép cộng bit XOR. Phép nhân được thực hiện theo modulo của đa thức bất khả qui của trường. Trong trường hợp thuật toán AES đó là đa thức x⁹ + x⁴ + x³ + x + 1.

Hình B.4 mô tả phép biến đổi MixColumns().

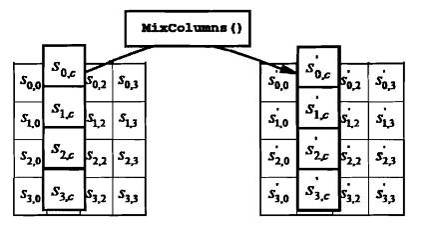
Hình B.4 – MixColumns() thao tác trên Trạng thái, thay cột bằng cột khác

B.1.7. Phép biến đổi MixColumns^-1()

MixColumns^-1() là phép biến đổi nghịch đảo của phép biến đổi MixColumns(). MixColumns^-1() thao tác trên Trạng thái, thay mỗi cột bằng cột khác. Phép biến đổi này có thể biểu diễn dưới dạng phép nhân ma trận, ở đấy mỗi byte được coi như một phần tử của trường hữu hạn GF(2⁸):

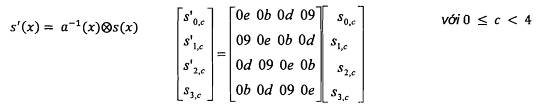
Kết quả của phép nhân là bốn byte trong mỗi cột được thay thế như sau:

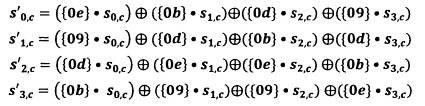
B.1.8. Phép biến đổi AddRoundKey()

Trong phép biến đổi AddRoundKey(), khóa vòng được cộng vào Trạng thái bằng phép cộng bit đơn giản XOR. Mỗi khóa vòng gồm bốn từ (128 bit) lấy từ lược đồ khóa (được mô tả tại 5.2.5). Bốn từ này được cộng vào cột Trạng thái như sau:

ở đây, 0 ≤ c < 4=”” và=””>W_(4*i+c) là các từ của lược đồ khóa thứ c của khóa vòng thứ i W_i = [w_(4*i),w_(4*i+1),w_(4*i+2),w_(4*i+3)] và i là giá trị thuộc khoảng 0 ≤ i ≤ Nr. Trong phép mã hóa, phép cộng khóa vòng ban đầu xảy ra khi i = 0, trước ứng dụng thứ nhất của hàm vòng. Việc áp dụng phép biến đổi AddRoundKey() cho Nr vòng của phép mã hóa xảy ra khi 1 ≤ i ≤ Nr.

Hoạt động của phép biến đổi AddRoundKey(), được minh họa trên Hình B.5. Địa chỉ byte trong các từ của lược đồ khóa được mô tả trong Điều 2.2.2.2.

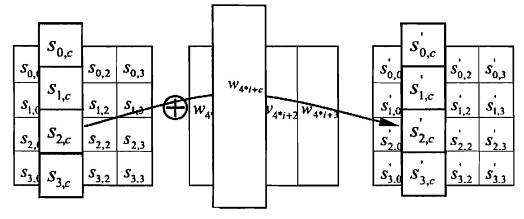
Hình B.5: AddRoundKey() cộng bit XOR từng cột của Trạng thái với mỗi từ lấy từ lược đồ khóa