Nội dung toàn văn Quy chuẩn kỹ thuật quốc gia QCVN 5:2016/BQP về Chữ ký số sử dụng trong lĩnh vực ngân hàng
QCVN 5 : 2016/BQP
QUY CHUẨN KỸ THUẬT QUỐC GIA VỀ CHỮ KÝ SỐ SỬ DỤNG TRONG LĨNH VỰC NGÂN HÀNG
National technical regulation on digital signature used in banking
MỤC LỤC
Lời nói đầu
1. QUY ĐỊNH CHUNG
1.1. Phạm vi điều chỉnh
1.2. Đối tượng áp dụng
1.3. Tài liệu viện dẫn
1.4. Giải thích từ ngữ
1.5. Các ký hiệu
2. QUY ĐỊNH KỸ THUẬT
2.1. Chữ ký số
2.1.1. Quy định kỹ thuật
2.1.2. Chữ ký số RSA-PSS
2.1.3. Chữ ký số ECDSA
2.1.4. Chữ ký số DSA
2.1.5. Chữ ký số RSASSA-PKCS1-v1_5
2.2. Hàm băm
3. QUY ĐỊNH VỀ QUẢN LÝ
4. TRÁCH NHIỆM CỦA TỔ CHỨC, CÁ NHÂN
5. TỔ CHỨC THỰC HIỆN
Lời nói đầu
QCVN 5 : 2016/BQP do Cục Quản lý mật mã dân sự và Kiểm định sản phẩm mật mã – Ban Cơ yếu Chính phủ biên soạn, Ban Cơ yếu Chính phủ trình duyệt, Bộ Khoa học và Công nghệ thẩm định và được ban hành theo Thông tư số 161/2016/TT-BQP ngày 21 tháng 10 năm 2016 của Bộ trưởng Bộ Quốc phòng.
QUY CHUẨN KỸ THUẬT QUỐC GIA VỀ CHỮ KÝ SỐ SỬ DỤNG TRONG LĨNH VỰC NGÂN HÀNG
National technical regulation on digital signature used in banking
1. QUY ĐỊNH CHUNG
1.1. Phạm vi điều chỉnh
Quy chuẩn kỹ thuật quốc gia này quy định mức giới hạn của các đặc tính kỹ thuật mật mã của chữ ký số sử dụng trong lĩnh vực ngân hàng.
1.2. Đối tượng áp dụng
Quy chuẩn này áp dụng đối với các doanh nghiệp kinh doanh sản phẩm, dịch vụ mật mã dân sự trong lĩnh vực ngân hàng; các tổ chức tín dụng (trừ quỹ tín dụng nhân dân cơ sở có tài sản dưới 10 tỷ, tổ chức tài chính vi mô) sử dụng sản phẩm, dịch vụ mật mã dân sự.
1.3. Tài liệu viện dẫn
– Recommendation for Random Number Generation Using Deterministic Random Bit Generators, NIST SP 800-90A Rev. 1, National Institute of Standards and Technology, June 2015. (Khuyến cáo cho bộ sinh số ngẫu nhiên sử dụng bộ sinh bit ngẫu nhiên tất định, NIST SP 800-90A Rev. 1, Viện tiêu chuẩn và công nghệ quốc gia (Mỹ), tháng 6 năm 2015).
– RSA Laboratories. PKCS#1 v2.1: RSA Cryptography Standard. June 2002. (Phòng thí nghiệm RSA. PKCS#1 v2.1: Tiêu chuẩn mật mã RSA. Tháng 6 năm 2002).
– TCVN 7635:2007 Kỹ thuật mật mã – Chữ ký số.
– NIST, Federal Information Processing Standards Publication 186-4, Digital Signature Standard (DSS), July 2013. (NIST, Tiêu chuẩn xử lý thông tin liên bang, Chuẩn chữ ký số (DSS), tháng 7 năm 2013).
– NIST, Federal Information Processing Standards Publication 180-4, Secure Hash Standard (SHS), August 2015. (NIST, Tiêu chuẩn xử lý thông tin liên bang, Chuẩn hàm băm an toàn (SHS), tháng 8 năm 2015).
1.4. Giải thích từ ngữ
Trong Quy chuẩn này, các từ ngữ dưới đây được hiểu như sau:
1.4.1. Thông tin không thuộc phạm vi bí mật nhà nước
Là thông tin không thuộc nội dung tin “tuyệt mật”, “tối mật” và “mật” được quy định tại Pháp lệnh Bảo vệ bí mật nhà nước ngày 28 tháng 12 năm 2000.
1.4.2. Mật mã
Là những quy tắc, quy ước riêng dùng để thay đổi hình thức biểu hiện thông tin nhằm bảo đảm bí mật, xác thực, toàn vẹn của nội dung thông tin.
1.4.3. Mật mã dân sự
Là kỹ thuật mật mã và sản phẩm mật mã được sử dụng để bảo mật hoặc xác thực đối với thông tin không thuộc phạm vi bí mật nhà nước.
1.4.4. Sản phẩm mật mã dân sự
Là các tài liệu, trang thiết bị kỹ thuật và nghiệp vụ mật mã để bảo vệ thông tin không thuộc phạm vi bí mật nhà nước.
1.4.5. Kỹ thuật mật mã
Là phương pháp, phương tiện có ứng dụng mật mã để bảo vệ thông tin.
1.4.6. Mã hóa
Phép biến đổi (khả nghịch) dữ liệu bởi thuật toán mật mã để tạo ra bản mã, tức là che giấu nội dung thông tin của dữ liệu.
14.7. Giải mã
Phép toán ngược với phép mã hóa tương ứng.
1.4.8.
Mật mã phi đối xứng
Hệ thống dựa trên kỹ thuật mật mã phi đối xứng, trong đó phép biến đổi công khai được sử dụng để mã hóa, phép biến đổi bí mật được sử dụng để giải mã.
1.4.9. Kỹ thuật mật mã phi đối xứng
Kỹ thuật mật mã phi đối xứng sử dụng hai phép biến đổi liên quan đến nhau, phép biến đổi công khai (được xác định bởi khóa công khai) và phép biến đổi bí mật (được xác định bởi khóa riêng). Cả hai phép biến đổi này có tính chất là cho biết phép biến đổi công khai, về mặt tính toán không thể có khả năng xác định được phép biến đổi bí mật.
1.4.10. Chữ ký số
Một chuỗi số, kết quả của phép biến đổi mật mã trên thông điệp dữ liệu nhằm cung cấp một phương tiện để kiểm tra tính xác thực của nguồn gốc thông điệp dữ liệu, tính toàn vẹn của dữ liệu và tính không thể chối bỏ của người đã ký.
1.5. Các ký hiệu
|
AES |
Tiêu chuẩn mã hóa tiên tiến (Advanced Encryption Standard) |
|
Octet |
Chuỗi bit có độ dài bằng 8 |
|
n |
Modulo RSA |
|
d |
Số mũ bí mật RSA |
|
e |
Số mũ công khai RSA |
|
(n,e) |
Khóa công khai RSA của người ký |
|
c |
Một biểu diễn của bản mã, là số nguyên thuộc (0,n-1) |
|
C |
Bản mã được biểu diễn ở dạng chuỗi octet |
|
EM |
Chuỗi Octet biểu diễn thông điệp đã được ghi mã |
|
emLen |
Độ dài theo Octet của EM |
|
k |
Độ dài modulo n tính theo octet |
|
m |
Một biểu diễn của thông điệp (văn bản), là số nguyên thuộc (0,n-1) |
|
M |
Thông điệp (văn bản), chuỗi octet |
|
I2OSP |
Hàm cơ sở chuyển đổi từ dạng số nguyên sang chuỗi octet (Integer-to-Octet-String Primitive) |
|
OS2IP |
Hàm cơ sở chuyển đổi từ chuỗi octet sang số nguyên (Octet- String-to-Integer-Primitive) |
|
LCM |
Bội chung nhỏ nhất (Least Common Multiplier) |
|
nlen |
Độ dài modulo n theo bit |
|
security_strength |
độ mạnh về an toàn (security_strength) là một số nguyên biểu thị lượng tính toán cần thiết để phá hệ mã |
|
N |
là ký hiệu độ dài theo bit của số nguyên tố q |
|
L |
là ký hiệu độ dài theo bit của số nguyên tố p |
|
|| |
Toán tử nối hai chuỗi |
|
PKCS |
Tiêu chuẩn mật mã khóa công khai (Puplic Key Cryptography Standard) do Phòng thí nghiệm RSA (Mỹ) ban hành. |
|
PSS |
Lược đồ ký xác suất (Probabilistic Signature Scheme) |
|
RSA |
Tên của hệ mã do ba nhà toán học Rivest, Shamir và Adleman RSA sáng tạo ra |
|
RSAVP |
Phép toán cơ sở phục vụ cho kiểm tra chữ ký RSA |
|
RSASP |
Phép toán ký RSA cơ sở |
|
RSASSA |
Lược đồ ký RSA kèm phụ lục (RSA Signature Scheme with Appendix) |
|
SHA |
Thuật toán băm an toàn (Secure Hash Algorithm). |
|
Word |
Từ (32 bit) |
|
DSA |
Thuật toán chữ ký số |
|
EC |
Đường cong Elliptic |
|
ECDSA |
Thuật toán chữ ký số dựa trên đường cong Elliptic |
2. QUY ĐỊNH KỸ THUẬT
2.1. Chữ ký số
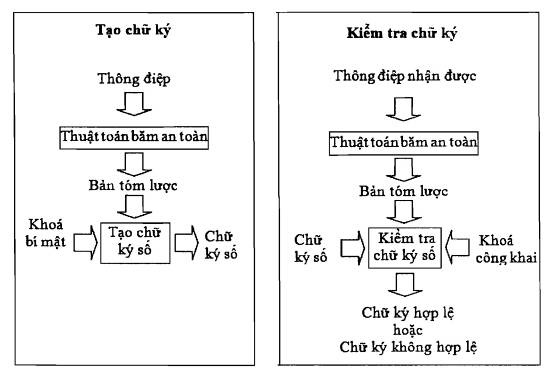
Hình 1 – Mô tả quá trình tạo và kiểm tra chữ ký số
Chữ ký số là một dạng chữ ký điện tử được tạo ra bằng sự biến đổi một thông điệp dữ liệu sử dụng hệ thống mật mã phi đối xứng theo đó người có được thông điệp dữ liệu ban đầu và khóa công khai của người ký có thể xác định được chính xác:
– Việc biến đổi nêu trên được tạo ra bằng đúng khóa bí mật tương ứng với khóa công khai trong cùng một cặp khóa;
– Sự toàn vẹn nội dung của thông điệp dữ liệu kể từ khi thực hiện việc biến đổi nêu trên.
Quá trình sinh chữ ký số trên một thông điệp dữ liệu yêu cầu sử dụng: 1) hàm băm mật mã thực hiện tính toán trên dữ liệu sẽ được ký, 2) sử dụng khóa mật mã và thuật toán ký để tạo chữ ký số trên đầu ra của hàm băm. Quy chuẩn này quy định sử dụng khóa mật mã trong thuật toán ký số, hàm băm mật mã được sử dụng trong quá trình sinh chữ ký số.
2.1.1. Quy định kỹ thuật
2.1.1.1. Quy định chung:
|
Quá trình chữ ký số |
Sử dụng |
Ghi chú |
|
Tạo chữ ký số |
Độ an toàn ≥ 112 bit: DSA: |p| ≥ 2048 và |q| ≥ 224 RSA: |n| ≥ 2048 EC: |n| ≥ 224 |
|
|
Xác thực chữ ký số |
Độ an toàn ≥ 112 bit: DSA: |p| ≥ 2048 và |q| ≥ 224 RSA: |n| ≥ 2048 EC: |n| ≥ 224 |
|
2.1.1.2. Quy định chi tiết về nguồn ngẫu nhiên:
Các số ngẫu nhiên được sử dụng cho các mục đích khác nhau như để sinh các tham số mật mã, các khóa mật mã, các giá trị ngẫu nhiên dùng một lần và các giá trị thách đố xác thực.
Một số bộ sinh bit ngẫu nhiên tất định DRBG được chấp thuận để sử dụng theo quy định chung bao gồm: HASH_DRBG, HMAC_DRBG và CTR_DRBG.
Các bộ sinh bit ngẫu nhiên RBG tuân theo SP800-90A phiên bản sửa đổi lại năm 2015 để sinh bit ngẫu nhiên cũng được chấp thuận để sử dụng tiếp.
2.1.2. Chữ ký số RSA-PSS
2.1.2.1. Các yêu cầu chung
1. Cặp khóa RSA dùng để ký thì không được dùng cho mục đích khác (chẳng hạn dùng lại để mã thông điệp);
2. Hai số nguyên tố p, q và số mũ bí mật d cần phải được giữ bí mật tránh việc bị truy cập bất hợp pháp, làm lộ hoặc sửa đổi. Modulo n và số mũ công khai e phải được công bố công khai;
3. Mỗi người sử dụng cần có Modulo n riêng;
4. Độ dài của Modulo n (nlen) không được nhỏ hơn 2048 bit và nên được thay đổi theo thời gian như sau.
|
Năm (y) |
độ an toàn |
nlen tối thiểu |
|
y<> |
112 |
2048 |
|
128 |
3072 |
Trong đó, độ mạnh về an toàn (security_strength) là một số nguyên biểu thị lượng tính toán cần thiết đề phá hệ mã.
Vì các phương pháp phá hệ mã thường xuyên được hoàn thiện nên cần phải định kỳ 3 đến 5 năm một lần xem xét lại nlen tối thiểu (có thể tham khảo chi tiết yêu cầu này trong tài liệu NIST Special Publication 800-57: Recommendation for Key Management – Part1: General, January 2016).
– Phiên bản áp dụng: Áp dụng phiên bản 2.1 của tiêu chuẩn RSA Cryptography Standard PKCS #1 v2.1.
– Áp dụng lược đồ RSAES-OAEP để mã hóa và RSASSA-PSS để ký.
2.1.2.2. Quy định chi tiết về các khóa RSA
1. Số mũ công khai e cần phải được chọn với các ràng buộc sau:
a) Số mũ công khai e cần được chọn trước khi tạo số mũ bí mật d;
b) Số mũ công khai e cần phải là số nguyên dương lẻ sao cho
65,537 ≤ e <>nlen-2security_strength
Với nlen là độ dài của modulo n theo bit.
Chú ý rằng e có thể là giá trị bất kỳ mà thỏa mãn ràng buộc 1(b); p và q sẽ được chọn (trong mục 2) sao cho e là nguyên tố cùng nhau với cả (p – 1) và (q – 1).
2. Hai số nguyên tố p và q được tạo ngẫu nhiên và giữ bí mật cần phải được chọn với các ràng buộc sau:
a) (p – 1) và (q – 1) cần phải là nguyên tố cùng nhau với số mũ công khai e;
b) Mỗi một trong bốn số (p + 1), (p – 1) và (q + 1), (q – 1) cần phải có các nhân tử nguyên tố lớn hơn 2security-strength+20;
c) Nhân tử nguyên tố bí mật p, q cần phải được chọn ngẫu nhiên từ các số nguyên tố thỏa mãn (![]() )(2(nlen/2)-1) ≤ q < p=”” ≤=””>(nlen/2) – 1);
)(2(nlen/2)-1) ≤ q < p=”” ≤=””>(nlen/2) – 1);
d) |p – q| > 2(nlen/2-100).
3. Số mũ bí mật d cần phải được lựa chọn sau khi tạo p và q với các ràng buộc:
a) Số mũ d cần phải lớn hơn 2(nlen/2), và
b) d = e–1mod(LCM((p – 1), (q – 1)))
(Chi tiết về hàm tạo các tham số RSA có thể tham khảo trong tài liệu FIPS 186-4: Digital Signature Standard).
2.1.2.3. Tạo chữ ký số
RSASSA – PSS – SIGN(K, M)
|
Đầu vào: |
K |
khóa bí mật RSA của người ký |
|
|
M |
thông điệp sẽ được ký, là một chuỗi octet |
|
Đầu ra: |
S |
chữ ký, chuỗi octet có độ dài k, với k là độ dài của modulo RSA theo octet |
|
Thông báo lỗi: |
|
“văn bản quá dài”, “lỗi định dạng” |
Các bước:
1. Mã hóa EMSA – PSS: Áp dụng thao tác EMSA – PSS – ENCODE vào văn bản M để tạo ra thông điệp được định dạng EM có độ dài é(modBits–1)/8ù octet sao cho độ dài bit của số nguyên OS2lP(EM) nhiều nhất là modBits– 1, với modBits là độ dài theo bit của số n (mođun RSA):
EM = EMSA – PSS – ENCODE (M,modBits – 1).
Chú ý rằng độ dài octet của EM sẽ bằng k -1 nếu modBits – 1 chia hết cho 8 và bằng k nếu modBits -1 không chia hết cho 8. Nếu hàm EMSA – PSS – ENCODE cho ra thông báo lỗi “văn bản quá dài” thì RSASSA – PSS – SIGN cũng cho ra thông báo lỗi “văn bản quá dài” và dừng lại. Nếu EMSA – PSS – ENCODE cho ra thông báo “lỗi định dạng” thì RSASSA – PSS – SIGN cũng cho ra thông báo “lỗi định dạng” và dừng lại.
2. Chữ ký RSA:
a. Chuyển thông điệp đã được định dạng (chuỗi octet) EM thành biểu diễn thông điệp ở dạng số nguyên m.
m = OS2IP (EM).
b. Áp dụng phép toán cơ sở RSASP với K là khóa bí mật RSA và Biểu diễn thông điệp m để tạo ra biểu diễn chữ ký là số nguyên s:
s = RSASP(K,m).
c. Chuyển chữ ký s dạng số nguyên thành chữ ký S dạng chuỗi octet có độ dài k:
s = I2OSP(s,k).
Đưa ra chữ ký S.
2.1.2.4. Xác thực chữ ký số
RSASSA – PSS – VERlFY((n, e), M, s)
|
Đầu vào: |
(n, e) |
khóa công khai RSA của người ký |
|
|
M |
thông điệp mà chữ ký của nó cần được kiểm tra, là chuỗi octet |
|
|
S |
chữ ký được kiểm tra, chuỗi octet có độ dài k, với k là độ dài theo octet của số n, modulo RSA |
|
Đầu ra: |
|
“chữ ký hợp lệ” hoặc “chữ ký không hợp lệ” |
Các bước:
1. Kiểm tra độ dài: Nếu độ dài của chữ ký S không là k octet, cho ra thông báo lỗi “chữ ký không hợp lệ” và dừng lại;
2. Kiểm tra chữ ký RSA;
a. Chuyển chữ ký S thành biểu diễn chữ ký ở dạng số nguyên s;
s = OS2IP(S)
b. Áp dụng phép toán cơ sở RSAVP với khóa công khai RSA là (n, e) và biểu diễn chữ ký s để tạo ra m là số nguyên biểu diễn thông điệp;
m = RSAVP((n,e),s)
c. Chuyển biểu diễn thông điệp m thành thông điệp đã được định dạng EM có độ dài emLen = é(modBits – 1)/8ù octet, với modBits là độ dài theo bit của số n (Modulo RSA):
EM = I2OSP (m, emLen)
Chú ý rằng emLen sẽ bằng k – 1 nếu modBits – 1 chia hết cho 8 và bằng k nếu modBits – 1 không chia hết cho 8. Nếu I2OSP cho ra thông báo lỗi “số nguyên quá lớn” thì RSASSA – PSS – VERIFY cho ra thông báo lỗi “chữ ký không hợp lệ” và dừng lại.
3. Kiểm tra EMSA – PSS: Áp dụng thao tác kiểm tra EMSA – PSS – VERIFY vào thông điệp m và thông điệp đã được định dạng EM để xác định xem chúng có tương ứng với nhau hay không;
Result = EMSA – PSS – VERIFY (M,EM,modBits – 1).
4. Nếu kết quả (Result) là “phù hợp” thì cho ra “chữ ký hợp lệ”. Ngược lại sẽ cho ra “chữ ký không hợp lệ”.
2.1.3. Chữ ký số ECDSA
2.1.3.1. Quy định chi tiết về các khóa ECDSA:
Kiểm tra tính hợp lệ của các tham số miền (p,SEED, a, b, G, n, h) như sau:
Xâu SEED dùng để sinh ngẫu nhiên đường cong Elliptic xác định trên trường Fp với p là số nguyên tố lẻ.
Trước khi sử dụng một bộ tham số miền, tính hợp lệ của nó phải được kiểm tra theo thuật toán dưới đây:
1. Kiểm tra p là một số nguyên tố lẻ.
2. Kiểm tra a, b, xG, yG là các phần tử của trường Fp.
3. Kiểm tra rằng a và b được dẫn xuất tương ứng từ SEED.
4. Kiểm tra (4a3 + 27b2) khác 0 và j(E) ≠ 0; 1728 trong Fp
5. Kiểm tra ![]() trong Fp.
trong Fp.
6. Kiểm tra n là nguyên tố và n > 4![]() .
.
7. Kiểm tra nG = 0E.
8. Kiểm tra đường cong có thuộc danh sách các đường cong yếu:
a. Thỏa mãn điều kiện MOV, (chú ý rằng một đường cong thỏa mãn điều kiện MOV sẽ không phải là đường cong siêu biến).
b. Kiểm tra đường cong không kì dị, nghĩa là #E ≠ p.
Nếu bất kỳ sự kiểm tra nào ở trên thất bại thì tham số miền phải được xem là không hợp lệ.
Điều kiện MOV được hiểu là không có giá trị k nguyên dương nào 0 k <>B để cho pk – 1 chia hết cho n. Trên thực hành hiện nay |p| = 224 bit thì người ta xét với B = 15 là đủ vì khi đó |pk| = 3360 > 2048.
Các hệ số a,b của đường cong được sinh ngẫu nhiên trên Fp từ đầu vào SEED và có thể kiểm tra được.
Khóa bí mật d phải được sinh ngẫu nhiên trong khoảng [1,n – 1].
Đường cong Elliptic xác định trên trường hữu hạn Fp với tối thiểu |p| = 224 bit và được xác định cụ thể như sau:
|
Độ dài bit của n |
Độ dài bit của p |
|
224 – 255 |
|p| = 224 |
|
256 – 383 |
|p| = 256 |
|
384-511 |
|p| = 384 |
|
≥ 512 |
|p| = 521 |
Đại lượng Cofactor được định nghĩa và ký hiệu là h = #E(Fp)/n tuân theo bảng dưới đây:
|
Độ dài bit của n |
Giá trị h cực đại cho phép |
|
224 – 255 |
214 |
|
256 – 383 |
216 |
|
384 – 511 |
224 |
|
≥ 512 |
232 |
2.1.3.2. Tạo chữ ký số
Thuật toán Chữ ký số Đường cong Elliptic (ECDSA) thực hiện việc sinh chữ ký của thông báo m, làm việc như sau:
Sinh chữ ký ECDSA
Đầu vào: Các tham số miền (E,P), khóa bí mật d, thông báo m.
Đầu ra: Chữ ký (r, s).
1. Lấy 0 k q một cách ngẫu nhiên
2. (xR,yR) ← kP
3. r ← xR mod q
4. Nếu r = 0 thì chuyển về bước 1
5. k ← k–1 mod q
6. e ← H(m)
7. s ← k(e + rd) mod q
8. Nếu s = 0 thì quay về bước 1
9. Trả về (r,s)
2.1.3.3. Xác thực chữ ký số
Để kiểm tra chữ ký số (r,s) của thông báo m, người kiểm tra tính các bước sau (Q = dP – ký hiệu khóa công khai):
Kiểm tra chữ ký ECDSA
Đầu vào: Các tham số miền (E,P), khóa công khai Q, thông báo m, chữ ký (r,s)
Đầu ra: Chấp nhận hoặc bác bỏ chữ ký.
1. Kiểm tra rằng 0 < r,s=””><>
2. s’ ← s-1 mod q
3. e ← H(m)
4. h1 ← s’e mod q
5. h2 ← s’r mod q
6. R = (xR, yR) ← h1P +h2Q
7. Nếu R = 0 thì bác bỏ chữ ký.
8. Nếu xR mod q = r thì chấp nhận, ngược lại thì bác bỏ.
2.1.4. Chữ ký số DSA
2.1.4.1. Quy định chi tiết về các khóa DSA:
Các tham số riêng bí mật k phải là số được sinh ngẫu nhiên 0 k q với độ dài |q| không nhỏ hơn 224 bit.
2.1.4.2. Tạo chữ ký số
Chọn N là độ dài bit của q,min(N, outlen) biểu thị số nguyên dương nhỏ nhất N và outlen là độ dài bit của khối đầu ra hàm băm.
Chữ ký của một thông điệp M bao gồm cặp số r và s được tính toán như sau:
r = (gk mod p) mod q.
z = các bit tận cùng bên trái min(N, outlen) của Hash(M).
s = (k-1(z + xr))mod q.
Khi tính s, xâu z thu được từ hàm Hash(M) sẽ được biến đổi sang một số nguyên.
Chú ý r có thể được tính bất cứ khi nào nếu biết k, p, q và g. Ví dụ: bất cứ khi nào các tham số miền p, q và g được biết, và k được tính toán trước thì r cũng có thể được tính trước vì thông tin của thông báo được ký không yêu cầu các tính toán của r. Việc tính trước giá trị k, k-1 và r sẽ được bảo vệ một cách tương tự như khóa riêng x tới khi tính toán xong s.
Giá trị của r và s sẽ được kiểm tra để xác định xem r = 0 hay s = 0. Nếu một trong hai r = 0 hoặc s = 0 thì một giá trị mới của k sẽ được sinh ra và chữ ký sẽ được tính toán lại. Nếu chữ ký số được sinh ra đúng đắn, thì rất hiếm khi xảy ra r = 0 hoặc s = 0.
Chữ ký (r,s) có thể được truyền đi cùng thông điệp để xác thực.
2.1.4.3. Xác thực chữ ký số
Gọi M’, r’ và s’ là các phiên bản tương ứng đã nhận được của M, r và s; gọi y là khóa công khai của người ký; gọi N là độ dài bit của q, và min(N, outlen) biểu thị số nguyên dương nhỏ nhất n và outlen, ở đây outlen là độ dài bit của khối đầu ra hàm băm.
Tiến trình xác thực chữ ký được thực hiện như sau:
1. Kiểm tra nếu một trong hai điều kiện 0 < r’=””>< q=””>và 0 < s’=””>< q=””>bị vi phạm thì chữ ký bị từ chối và được coi là không hợp lệ.
2. Nếu cả hai điều kiện ở bước 1 được thỏa mãn thì:
w = (s’)–1mod q
z = Các bit tận cùng bên trái min(N, outlen) của Hash(M’).
u1 = (zw) mod q.
u2 = ((r’)w) mod q.
v = (((g)u1 (y)u2) mod p) mod q.
3. Nếu v = r’, khi đó chữ ký được xác thực.
4. Nếu v khác r’, khi đó thông báo hoặc chữ ký có thể đã bị thay đổi, có thể do lỗi trong tiến trình sinh chữ ký hoặc chữ ký có thể bị giả mạo.
2.1.5. Chữ ký số RSASSA-PKCS1-v1_5
2.1.5.1. Các yêu cầu chung
1. Cặp khóa RSA dùng để ký thì không được dùng cho mục đích khác (chẳng hạn dùng lại để mã thông điệp);
2. Hai số nguyên tố p, q và số mũ bí mật d cần phải được giữ bí mật tránh việc bị truy cập bất hợp pháp, làm lộ hoặc sửa đổi. Modulo n và số mũ công khai e phải được công bố công khai;
3. Mỗi người sử dụng cần có Modulo n riêng;
4. Độ dài của Modulo n (nlen) không được nhỏ hơn 2048 bit và nên được thay đổi theo thời gian như sau.
|
Năm (y) |
độ an toàn |
nlen tối thiểu |
|
y<> |
112 |
2048 |
|
128 |
3072 |
Trong đó, độ mạnh về an toàn (security_strength) là một số nguyên biểu thị lượng tính toán cần thiết để phá hệ mã.
Vì các phương pháp phá hệ mã thường xuyên được hoàn thiện nên cần phải định kỳ 3 đến 5 năm một lần xem xét lại nlen tối thiểu (có thể tham khảo chi tiết yêu cầu này trong tài liệu NIST Special Publication 800-57: Recommendation for Key Management – Part1: General, January 2016).
2.1.5.2. Quy định chi tiết về các khóa RSA
1. Số mũ công khai e cần phải được chọn với các ràng buộc sau:
a) Số mũ công khai e cần được chọn trước khi tạo số mũ bí mật d;
b) Số mũ công khai e cần phải là số nguyên dương lẻ sao cho
65,537 ≤ e <>nlen-2security-strength
Với nlen là độ dài của modulo n theo bit.
Chú ý rằng e có thể là giá trị bất kỳ mà thỏa mãn ràng buộc 1(b); p và q sẽ được chọn (trong mục 2) sao cho e là nguyên tố cùng nhau với cả (p – 1) và (q – 1).
2. Hai số nguyên tố p và q được tạo ngẫu nhiên và giữ bí mật cần phải được chọn với các ràng buộc sau:
a) (p – 1) và (q – 1) cần phải là nguyên tố cùng nhau với số mũ công khai e;
b) Mỗi một trong bốn số (p + 1), (p – 1) và (q + 1), (q – 1) cần phải có các nhân tử nguyên tố lớn hơn 2security-strength+20;
c) Nhân tử nguyên tố bí mật p, q cần phải được chọn ngẫu nhiên từ các số nguyên tố thỏa mãn (![]() )(2(nlen/2)-1) ≤ q < p=”” ≤=””>(nlen/2) – 1);
)(2(nlen/2)-1) ≤ q < p=”” ≤=””>(nlen/2) – 1);
d) |p – q| > 2(nlen/2-100).
3. Số mũ bí mật d cần phải được lựa chọn sau khi tạo p và q với các ràng buộc:
a) Số mũ d cần phải lớn hơn 2(nlen/2), và
b) d = e–1mod(LCM((p – 1), (q – 1)))
(Chi tiết về hàm tạo các tham số RSA có thể tham khảo trong tài liệu FIPS 186-4: Digital Signature Standard).
2.1.5.3 Tạo chữ ký số
RSASSA – PKCS1 – V1_5 – SIGN (K,M)
|
Đầu vào: |
K |
khóa bí mật RSA của người ký |
|
|
M |
thông báo được ký theo xâu bộ 8 |
|
Đầu ra: |
S |
Chữ ký, một xâu bộ 8 của độ dài k trong đó k là độ dài theo bộ 8 của RSA modulo n |
|
Các lỗi |
|
“Thông báo quá dài”; “Modulo RSA quá ngắn” |
Các bước thực hiện:
1. Mã hóa EMSA-PKCS1–v1_5:
Áp dụng mã hóa EMSA-PKCS1-v1_5 đối với thông báo M để tạo ra bản mã EM có độ dài là k bộ 8.
EM = EMSA – PKCS1 – V1_5 – ENCODE (M,k).
2. Chữ ký RSA:
a) Biến đổi bản mã EM thành số nguyên m
m = OS2IP(EM).
b) Áp dụng chữ ký số nguyên thủy RSASP1 cho khóa riêng K và thông điệp m để tạo ra số nguyên s
s = RSASP1 (K,m).
c. Biến đổi s tương ứng thành chữ ký s có độ dài k bộ 8
S = I2OSP (s, k).
3. Đưa ra chữ ký S.
2.1.5.4. Xác thực chữ ký số
RSASSA – PKCS1 – V1-5 – VERIFY ((n,e),M,S)
|
Đầu vào: |
(n, e) |
khóa công khai RSA của người ký |
|
|
M |
thông báo (chữ ký số) cần xác thực theo xâu bộ 8 |
|
|
S |
Chữ ký cần xác thực là xâu bộ 8 độ dài k trong đó k là độ dài theo 8 bộ của RSA modulo n |
|
Đầu ra: |
|
“Chữ ký hợp lệ” hoặc “chữ ký không hợp lệ” |
|
Các lỗi: |
|
“Thông điệp quá dài”; “Modulo RSA quá ngắn” |
Các bước thực hiện:
1. Kiểm tra độ dài: Nếu độ dài của chữ ký s không phải là k các bộ 8 thì xuất đầu ra “chữ ký không hợp lệ” và dừng lại.
2. Xác thực RSA:
a. Biến đổi S thành số nguyên s
s = OS2IP(S)
b. Sử dụng RSAVP1 nguyên thủy cho khóa RSA công khai (n,e) và s để tạo ra số nguyên m
m = RSAVP1 ((n,e),s).
Nếu đầu ra RSAVP “chữ ký số đại diện nằm ngoài dải hợp lệ” thì đưa ra “chữ ký số không hợp lệ” và dừng lại.
c. Biến đổi m thành EM có độ dài k các bộ 8:
EM = I2OSP (m,k).
Nếu đầu ra I2OSP “số nguyên quá lớn” thì đưa ra “chữ ký số không hợp lệ” và dừng lại.
3. EMSA-PKCS1-v1_5 encoding:
Áp dụng mã hóa EMSA-PKCS1-v1_5 đối với thông điệp M để tạo ra bản mã thứ 2 EM’ có độ dài k các bộ 8:
EM’ = EMSA – PKCS1 – V1_5 – ENCODE (M, k).
4. So sánh EM và EM’ nếu giống nhau thì chữ ký hợp lệ, ngược lại chữ ký là không hợp lệ.
2.2. Hàm băm
Hàm băm: Một thuật toán chuyển đổi mỗi thông báo biểu diễn dưới dạng bit có độ dài bất kỳ thành một chuỗi bit có độ dài cố định. Chuỗi bit có độ dài cố định đó được gọi là “giá trị băm”, “mã băm”, hai đơn giản là “tóm lược” của thông báo đầu vào. Các thuật toán băm mật mã được thiết kế sao cho thỏa mãn các tính chất sau:
– Tính một chiều hay tính kháng tiền ảnh: Không thể tìm được trong thời gian cho phép một thông báo có giá trị băm cho trước;
– Tính kháng tiền ảnh thứ hai: Cho trước thông điệp M1, không thể tìm được trong thời gian cho phép một thông điệp M2 khác M1 sao cho giá trị băm của M1 và M2 là như nhau;
– Tính kháng xung đột: Không thể tìm được hai chuỗi bit khác nhau có cùng một giá trị băm.
Trong Quy chuẩn này các hàm băm sau đây được phép sử dụng.
|
Độ an toàn |
Hàm băm áp dụng |
|
128 |
SHA-256, SHA-512/256, SHA3–256 |
|
192 |
SHA-384, SHA3-384 |
|
≥ 256 |
SHA-512, SHA3-512 |
3. QUY ĐỊNH VỀ QUẢN LÝ
3.1. Các mức giới hạn của đặc tính kỹ thuật mật mã và yêu cầu quản lý của chữ ký số nêu tại Quy chuẩn này là các chỉ tiêu chất lượng phục vụ được quản lý theo quy định về quản lý chất lượng sản phẩm, dịch vụ mật mã dân sự được quy định tại Luật An toàn thông tin mạng ngày 19 tháng 11 năm 2015.
3.2. Hoạt động kiểm tra chất lượng sản phẩm, dịch vụ mật mã được cơ quan quản lý nhà nước có thẩm quyền tiến hành định kỳ hàng năm hoặc đột xuất.
3.3. Một số quy định về ngưỡng thời gian và độ an toàn khóa cụ thể:
– Quy định nghiệp vụ chung đối với độ an toàn khóa mật mã:
|
Độ an toàn theo bit |
Thời hạn sử dụng quy định |
|
96 |
Đến cuối năm 2020 |
|
112 |
Đến cuối năm 2030 |
|
≥ 128 |
Từ năm 2030 |
– Thời hạn sử dụng được quy định chi tiết đối với độ an toàn khóa mật mã khóa công khai tính theo bit:
|
Thời hạn Quy định |
RSA |
DSA |
ECDSA |
|
2020 |
|p| = 1536 |
|p| = 1536, |q| = 192 |
192 – 224 |
|
2030 |
|p| = 2048 |
|p| = 2048, |q| = 224 |
224 – 255 |
|
Sau 2030 |
|p| = 3072 |
|p| = 3072, |q| = 256 |
256 |
– Các hàm băm tương ứng theo Độ an toàn bit:
|
Hàm băm |
Độ an toàn |
|
SHA-224 |
112 |
|
SHA-256 |
128 |
|
SHA-512 |
256 |
|
SHA-384 |
192 |
|
WHIRLPOOL |
256 |
– Độ an toàn theo bit quy đổi giữa RSA, DSA và ECDSA như sau:
|
Độ an toàn |
ECDSA |
RSA |
DSA |
|
112 |
224 |
2048 |
2048 |
|
128 |
256 |
3072 |
3072 |
|
192 |
384 |
7680 |
7680 |
|
256 |
512 |
15360 |
15360 |
3.4. Quy định về an toàn cài đặt và sử dụng:
Các thuật toán chữ ký số khi cài đặt phần mềm và phần cứng còn cần có đủ khả năng chống lại các tấn công kênh kề nhất là chống lại việc tính ra được các bit khóa trong quá trình thực hiện thuật toán.
4. TRÁCH NHIỆM CỦA TỔ CHỨC, CÁ NHÂN
4.1. Các tổ chức tín dụng (trừ quỹ tín dụng nhân dân cơ sở có tài sản dưới 10 tỷ, tổ chức tài chính vi mô) sử dụng sản phẩm, dịch vụ mật mã dân sự có trách nhiệm đảm bảo tuân thủ Quy chuẩn này và chịu sự kiểm tra của cơ quan quản lý nhà nước theo quy định.
4.2. Doanh nghiệp cung cấp sản phẩm, dịch vụ mật mã dân sự cho các tổ chức tín dụng (trừ quỹ tín dụng nhân dân cơ sở có tài sản dưới 10 tỷ, tổ chức tài chính vi mô) có trách nhiệm thực hiện công bố hợp quy sản phẩm, dịch vụ mật mã dân sự phù hợp với Quy chuẩn này. Việc công bố hợp quy thực hiện theo Thông tư số 28/2012/TT-BKHCN ngày 12 tháng 12 năm 2012 của Bộ Khoa học và Công nghệ.
4.3. Cục Quản lý mật mã dân sự và Kiểm định sản phẩm mật mã – Ban Cơ yếu Chính phủ có trách nhiệm tiếp nhận đăng ký công bố hợp quy, thực hiện quản lý, hướng dẫn và kiểm tra việc công bố hợp quy.
5. TỔ CHỨC THỰC HIỆN
5.1. Cục Quản lý mật mã dân sự và Kiểm định sản phẩm mật mã – Ban Cơ yếu Chính phủ có trách nhiệm hướng dẫn, tổ chức triển khai quản lý kỹ thuật mật mã của Chữ ký số theo Quy chuẩn này.
5.2. Trong trường hợp các quy định nêu tại Quy chuẩn kỹ thuật quốc gia này có sự thay đổi, bổ sung hoặc được thay thế thì thực hiện theo quy định tại văn bản mới./.


