Nội dung toàn văn Tiêu chuẩn quốc gia TCVN 10431-7:2014 (ISO 11843-7:2012) về Năng lực phát hiện – Phần 7: Phương pháp luận dựa trên tính chất ngẫu nhiên của nhiễu phương tiện đo
TIÊU CHUẨN QUỐC GIA
TCVN 10431-7:2014
ISO 11843-7:2012
NĂNG LỰC PHÁT HIỆN – PHẦN 7: PHƯƠNG PHÁP LUẬN DỰA TRÊN TÍNH CHẤT NGẪU NHIÊN CỦA NHIỄU PHƯƠNG TIỆN ĐO
Capability of detection – Part 7: Methodology based on stochastic properties of instrumental noise
Lời nói đầu
TCVN 10431-7:2014 hoàn toàn tương đương với ISO 11843-7:2012;
TCVN 10431-7:2014 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Bộ TCVN 10431 (ISO 11843), Năng lực phát hiện, gồm các tiêu chuẩn sau:
– TCVN 10431-1:2014 (ISO 11843-1:1997), Phần 1: Thuật ngữ và định nghĩa;
– TCVN 10431-2:2014 (ISO 11843-2:2000), Phần 2: Phương pháp luận trong trường hợp hiệu chuẩn tuyến tính;
– TCVN 10431-3:2014 (ISO 11843-3:2003), Phần 3: Phương pháp luận xác định giá trị tới hạn đối với biến đáp ứng khi không sử dụng dữ liệu hiệu chuẩn;
– TCVN 10431-4:2014 (ISO 11843-4:2003), Phần 4: Phương pháp luận so sánh giá trị tối thiểu phát hiện được với giá trị đã cho;
– TCVN 10431-5:2014 (ISO 11843-5:2008), Phần 5: Phương pháp luận trong trường hợp hiệu chuẩn tuyến tính và phi tuyến;
– TCVN 10431-6:2014 (ISO 11843-6:2013), Phần 6: Phương pháp luận xác định giá trị tới hạn và giá trị tối thiểu phát hiện được trong phép đo có phân bố Poisson được xấp xỉ chuẩn;
– TCVN 10431-7:2014 (ISO 11843-7:2012), Phần 7: Phương pháp luận dựa trên tính chất ngẫu nhiên của nhiễu phương tiện đo.
Lời giới thiệu
Bộ TCVN 10431 (ISO 11843) dựa trên phân bố xác suất của biến trạng thái tịnh (đại lượng đo) đối với tình huống hiệu chuẩn tuyến tính và phi tuyến. Điều này ngầm hiểu, mặc dù đôi khi nói rõ, là độ không đảm bảo kèm theo ước lượng của đáp ứng đo được chủ yếu xuất phát từ nhiễu cơ sở trong phân tích phương tiện đo. Trong nhiều, nhưng không phải hầu hết, các phương tiện phân tích, nhiễu cơ sở được coi là nguyên nhân chính của độ không đảm bảo khi lượng lấy mẫu nhỏ bằng giá trị tối thiểu phát hiện được. Trong phạm vi ứng dụng của mình, phương pháp nêu trong tiêu chuẩn này có thể không cần lặp lại nhiều mẫu thực tế, do đó giúp cải thiện môi trường toàn cầu bằng việc tiết kiệm thời gian và năng lượng mà việc lặp lại đòi hỏi.
Khái niệm cơ bản của tiêu chuẩn này là mô tả toán học phân bố xác suất của biến đáp ứng dưới dạng các quá trình ngẫu nhiên xác định rõ về mặt toán học. Mô tả này dễ dàng dẫn đến giá trị tối thiểu phát hiện được. Như đối với quan hệ giữa đáp ứng và đại lượng đo, có thể áp dụng các hàm hiệu chuẩn tuyến tính và phi tuyến. Theo cách này, sự tương thích với TCVN 10431-2 (ISO 11843-2) và TCVN 10431-5 (ISO 11843-5) được đảm bảo.
Định nghĩa và khả năng áp dụng của giá trị tối thiểu phát hiện được được mô tả trong TCVN 10431-1 (ISO 11843-1) và TCVN 10431-2 (ISO 11843-2); định nghĩa và khả năng áp dụng của biên dạng độ chụm được mô tả trong TCVN 10431-5 (ISO 11843-5). Biên dạng độ chụm thể hiện cách thức các thay đổi độ chụm phụ thuộc vào biến trạng thái tịnh. Tiêu chuẩn này quy định ứng dụng thực tế của các khái niệm cơ bản trong bộ TCVN 10431 (ISO 11843) trong trường hợp nhiễu nền chiếm ưu thế trong phân tích phương tiện đo.
Giá trị tối thiểu phát hiện được, xd, thường được biểu thị theo đơn vị của biến trạng thái tịnh. Nếu hàm hiệu chuẩn là tuyến tính thì SD hoặc CV của biến đáp ứng ước lượng trong tiêu chuẩn này có thể được biến đổi tuyến tính thành SD hoặc CV của biến trạng thái tịnh, chúng lần lượt có thể sử dụng cho việc ước lượng giá trị tối thiểu phát hiện được, xd.
Nếu hàm hiệu chuẩn là phi tuyến, biên dạng độ chụm của biến đáp ứng trong tiêu chuẩn này cần được chuyển đổi thành biên dạng độ chụm của biến trạng thái tịnh như trình bày TCVN 10431-5 (ISO 11843-5). Trong trường hợp này, có thể sử dụng nội dung của TCVN 10431-5 (ISO 11843-5) cho mục đích này mà không cần sửa đổi nhỏ nào.
NĂNG LỰC PHÁT HIỆN – PHẦN 7: PHƯƠNG PHÁP LUẬN DỰA TRÊN TÍNH CHẤT NGẪU NHIÊN CỦA NHIỄU PHƯƠNG TIỆN ĐO
Capability of detection – Part 7: Methodology based on stochastic properties of instrumental noise
1. Phạm vi áp dụng
Nhiễu nền tồn tại ở mọi nơi trong các phương tiện phân tích, cho dù có sử dụng mẫu cho phương tiện đó hay không. Tiêu chuẩn này đề cập đến các phương pháp luận toán học cho việc ước lượng giá trị tối thiểu phát hiện được trong trường hợp nguồn gây ra độ không đảm bảo đo chiếm ưu thế nhất là nhiễu nền. Giá trị tối thiểu phát hiện được có thể được suy trực tiếp và tính toán từ các đặc trưng ngẫu nhiên của nhiễu nền.
Tiêu chuẩn này quy định các phương pháp cơ bản để:
– lấy ra các tính chất ngẫu nhiên của nhiễu nền,
– sử dụng các tính chất ngẫu nhiên để ước lượng độ lệch chuẩn (SD) hoặc hệ số biến động (CV) của biến đáp ứng, và
– tính giá trị tối thiểu phát hiện được dựa trên SD hoặc CV thu được ở trên.
Các phương pháp mô tả trong tiêu chuẩn này rất hữu ích cho việc kiểm tra phát hiện một chất nào đó bằng nhiều loại thiết bị đo khác nhau, trong đó nhiễu nền của đầu ra phương tiện đo chiếm ưu thế hơn các nguồn độ không đảm bảo đo khác. Các lựa chọn khả thi có thể thấy rõ và phổ hấp thụ cực tím, phổ hấp thụ nguyên tử, phổ huỳnh quang nguyên tử, phổ phát quang, sắc ký lỏng và sắc ký khí.
2. Tài liệu viện dẫn
Các tài liệu viện dẫn trong tiêu chuẩn này rất cần thiết cho việc áp dụng tiêu chuẩn. Đối với các tài liệu có ghi năm công bố thì áp dụng bản được nêu. Đối với các tài liệu không ghi năm công bố thì áp dụng phiên bản mới nhất, bao gồm cả các sửa đổi.
TCVN 10431-1:2014 (ISO 11843-1:1997), Năng lực phát hiện – Phần 1: Thuật ngữ và định nghĩa
TCVN 10431-2:2014 (ISO 11843-2:2000), Năng lực phát hiện – Phần 2: Phương pháp luận trong trường hợp hiệu chuẩn tuyến tính
TCVN 10431-5:2014 (ISO 11843-5:2008), Năng lực phát hiện – Phần 5: Phương pháp luận trong trường hợp hiệu chuẩn tuyến tính và phi tuyến
TCVN 8244-1 (ISO 3534-1), Thống kê học – Từ vựng và ký hiệu – Phần 1: Thuật ngữ chung về thống kê và thuật ngữ dùng trong xác suất
TCVN 8244-2 (ISO 3534-2), Thống kê học – Từ vựng và ký hiệu – Phần 2: Thống kê ứng dụng ISO 3534-3, Statistics − Vocabulary and symbols − Part 3: Design of experiments (Thống kê học – Từ vựng và ký hiệu – Phần 3: Thiết kế thực nghiệm)
TCVN 6910-1 (ISO 5725-1), Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 1: Nguyên tắc và định nghĩa chung
3. Thuật ngữ và định nghĩa
Tiêu chuẩn này áp dụng các thuật ngữ và định nghĩa trong TCVN 8244-1 (ISO 3534-1), TCVN 8244-2 (ISO 3534-2), ISO 3534-3, TCVN 6910-1 (ISO 5725-1), TCVN 10431-1 (ISO 11843-1), TCVN 10431-2 (ISO 11843-2), TCVN 10431-5 (ISO 11843-5) và các thuật ngữ, định nghĩa dưới đây. Danh mục ký hiệu và từ viết tắt sử dụng trong tiêu chuẩn này được cho trong Phụ lục A.
3.1.
Biên dạng độ chụm (precision profile)
sY(X)] hoặc biến trạng thái tịnh [sX(X)] như là hàm số của biến trạng thái tịnh.
[TCVN 10431-5 (ISO 11843-5), định nghĩa 3.4].
CHÚ THÍCH 1: Hệ số biến động (CV) của biến đáp ứng hoặc biến trạng thái tịnh là hàm số của biến trạng thái tịnh cũng được gọi là biên dạng độ chụm.
CHÚ THÍCH 2: Độ chụm nghĩa là SD hoặc CV của biến đáp ứng hay SD hoặc CV của biến trạng thái tịnh khi ước lượng bằng hàm hiệu chuẩn [TCVN 10431-5 (ISO 11843-5)].
3.2.
Giá trị tối thiểu phát hiện được của biến trạng thái tịnh (minimum detectable value of the net state variable)
xd
Giá trị của biến trạng thái tịnh ở trạng thái thực tế, với xác suất 1 – b, sẽ dẫn đến kết luận là hệ thống không nằm trong trạng thái cơ sở.
CHÚ THÍCH 1: Với giả định là SD, sX(X), của biến trạng thái tịnh là hằng số [sX(X) = sX], giá trị tối thiểu phát hiện được, xd, được xác định là
xd = (kc + kd)sX (1)
trong đó
kc ký hiệu cho hệ số để quy định xác suất sai lầm loại một;
kc là hệ số để quy định xác suất sai lầm loại hai.
Nếu SD, sY, của biến đáp ứng được giả định là hằng số, [sY(X) = sY], thì giá trị tối thiểu phát hiện được có thể được tính bằng công thức sau:
xd = (kc + kd)(sY/ldY/dXl (2)
trong đó ldY/dXl ký hiệu cho giá trị tuyệt đối độ dốc của hàm hiệu chuẩn tuyến tính và là hằng số.
CHÚ THÍCH 2: Nếu biến trạng thái tịnh có phân bố chuẩn thì hệ số kc = kd = 1,65 quy định xác suất sai lầm loại một và loại hai (=5 %) và công thức (1) có thể viết đơn giản là xd = 3,30sX.
CHÚ THÍCH 3: Nếu kc = kd = 1,65, công thức (1) có dạng sX /xd = 1/3,30 = 30 %. Do đó, xd có thể tìm trong biên dạng độ chụm, xd nằm tại X, CV của nó là 30 %.
CHÚ THÍCH 4: Các loại biên dạng độ chụm khác được xác định nhưng chúng có thể chuyển đổi lẫn nhau.
Ví dụ, SD, sY(X), của biến đáp ứng có thể chuyển đổi thành SD, sX(X), của biến trạng thái tịnh bằng giá trị tuyệt đối của đạo hàm, ldY/dXl, của hàm hiệu chuẩn [Y = f(X)] : sX (X) = sY(X)/ldY/dXl [TCVN 10431-5 (ISO 11843-5)]. Xử lý này là một phép tính gần đúng, mức độ của nó phụ thuộc vào đường cong cục bộ, liên quan đến d2Y/dX2.
CHÚ THÍCH 5: Lấy từ TCVN 10431-5:2014 (ISO 11843-5:2008).
4. Phân tích định lượng và nhiễu nền
4.1. Nguồn sai số của phép phân tích
Việc phân tích định lượng để thu được đại lượng đo từ mẫu thường được coi là bao gồm việc chuẩn bị, phân tích bằng phương tiện đo, xử lý dữ liệu và hiệu chuẩn. Các bước phân tích này độc lập với nhau về mặt cơ học và vì vậy cũng độc lập về mặt xác suất.
Tiêu chuẩn này chỉ áp dụng cho việc phân tích bằng phương tiện đo. Tuy nhiên, sai số từ các bước khác cũng ảnh hưởng đến sai số của giá trị cuối của đại lượng đo. Đó là, độ không đảm bảo tổng hợp đi kèm với ước lượng của đại lượng đo phụ thuộc vào sự lan truyền tất cả các độ không đảm bảo gắn với các bước liên quan. Các điều kiện dưới đây là cần thiết để sử dụng tiêu chuẩn này.
Ở những nồng độ gần bằng giá trị tối thiểu phát hiện được trong phép sắc ký, sai số từ việc đưa mẫu vào máy sắc ký thậm chí còn ít quan trọng (ví dụ, CV = 0,3 % trong thiết bị mới) hơn so với nhiễu nền (CV = 30 % theo định nghĩa). Nếu tầm quan trọng của một yếu tố không phải nhiễu so sánh được với tầm quan trọng của nhiễu thì phương pháp luận của tiêu chuẩn này không áp dụng được.
Xử lý dữ liệu thường là quá trình lấy thành phần tín hiệu từ đầu ra thiết bị có nhiễu như chiều cao hoặc diện tích đỉnh, tương ứng là chiều cao tương đối đỉnh của tín hiệu có dạng đỉnh hoặc tích hợp các cường độ trên một vùng tín hiệu. Ảnh hưởng thống kê của quá trình này là quan tâm chính của tiêu chuẩn này. Việc sử dụng bộ lọc số hoặc tương tự cũng có thể được tính đến, nếu nhiễu sau lọc được phân tích cho mục đích này.
4.2. Các quá trình ngẫu nhiên trong nền
Ví dụ điển hình về biến đáp ứng là diện tích và chiều cao đo được trên máy sắc ký. Trong tiêu chuẩn này, chênh lệch cường độ [công thức (6)] và diện tích [công thức (10) và (11)] được lấy là hiệu và tổng các cường độ Yi của đầu ra thiết bị. Các biến đáp ứng thường độc lập với nhau ngay cả khi chúng thu được từ phép đo liên tiếp bởi cùng một thiết bị đo. Mặt khác, các cường độ liên tiếp Yi được lập công thức như một quá trình ngẫu nhiên phụ thuộc thời gian, và trong nhiều trường hợp, có thể coi là 1/f nhiễu.[1]
Phổ công suất, P(f), của 1/f nhiễu có độ dốc tỷ lệ nghịch với tần số f.
P(f) ![]() (3)
(3)
khi f gần bằng “không”.
Trong lý thuyết toán, mô hình đơn giản nhất của quá trình ngẫu nhiên là nhiễu trắng. Lấy wi ký hiệu cho biến ngẫu nhiên của nhiễu trắng tại điểm i. Theo định nghĩa, trung bình của nhiễu trắng bằng “không” và SD, ![]() , của nhiễu trắng là hằng số tại mọi điểm i. Đặc điểm nổi bật của nhiễu trắng là cường độ nhiễu, wi và wj, độc lập với nhau, nếu i ¹ j.
, của nhiễu trắng là hằng số tại mọi điểm i. Đặc điểm nổi bật của nhiễu trắng là cường độ nhiễu, wi và wj, độc lập với nhau, nếu i ¹ j.
Quá trình Markov là một mô hình toán học trong đó cường độ, Mi và Mj, phụ thuộc lẫn nhau(i ¹ j). Quá trình Markov được coi như thành phần chính của những thay đổi phụ thuộc thời gian của đầu ra thiết bị [xem công thức (9)]. Quá trình Markov tại điểm i được xác định là có dạng:
Mi = rMi=1 + mi (4)
trong đó
mi ký hiệu cho biến ngẫu nhiên của nhiễu trắng tại điểm i;
r là tham số không đổi (-1 <>r <>
5. Lý thuyết độ chụm
5.1. Lý thuyết dựa trên hàm tự hiệp phương sai
Lý thuyết do Winefordner[2][3][4] và các cộng sự đề xuất dựa trên hàm tự hiệp phương sai
![]() (5)
(5)
trong đó E[×] ký hiệu cho trung bình của biến ngẫu nhiên trong ngoặc vuông tại t0.
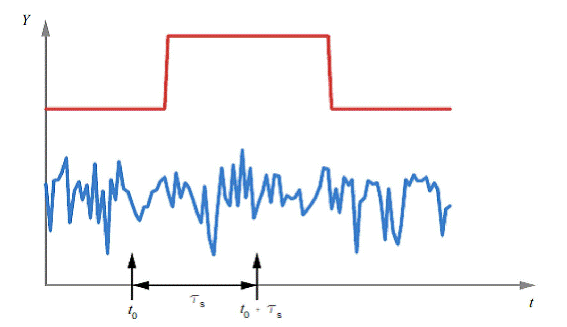
Hình 1 – Tín hiệu (đường phía trên) và nhiễu (đường phía dưới) với chênh lệch về cường độ
Phần phía trên của Hình 1 mô tả tín hiệu như (xấp xỉ với) xung chữ nhật. Nhiễu (cấu thành nhiễu nền) trên tín hiệu được mô tả như đường cong dao động ở phần phía dưới của hình. t0 ký hiệu giá trị thời gian trên tỷ lệ nền của tín hiệu và t0 + ts ký hiệu giá trị thời gian của bản thân tín hiệu. Phép đo (đọc tín hiệu) là hiệu các cường độ tại thời điểm t0 và t0+ ts. Giá trị của tín hiệu có thể bằng “không” tại t0 khi không có nhiễu nền. Tín hiệu có giá trị có hạn tại t0 + ts khi mẫu được đo. Trong mô hình đo của tiêu chuẩn này, tín hiệu và nhiễu được xếp chồng và quá trình ngẫu nhiên này có giá trị Yi tại thời điểm ti. Cường độ tại các thời điểm t0 và t0 + ts được mô tả tương ứng là ![]() và
và ![]() , và chênh lệch cường độ được cho bởi công thức (6).
, và chênh lệch cường độ được cho bởi công thức (6).
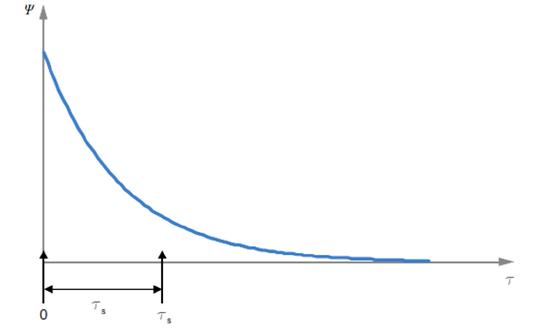
Hình 2 – Hàm tự hiệp phương sai của nhiễu
Chênh lệch giữa các giá trị của hàm tự hiệp phương sai, y(t) tại 0 và ts cho vế phải của công thức (7).
Gần giá trị tối thiểu phát hiện được, được đọc theo dao động nền, chênh lệch cường độ thường áp dụng trong quang phổ kế phân tích. Định nghĩa của chênh lệch cường độ, ví dụ số đọc tín hiệu hiệu chính cho nhiễu nền, là [2][3][4]
![]() (6)
(6)
Ở đây, DY tương ứng với biến đáp ứng Y. Phương sai của chênh lệch cường độ được viết như trong công thức (7) [2][3][4]. [Về dẫn xuất của công thức (7), xem Phụ lục B.]
sDY2 = 2[y(0) – y(ts)] (7)
Công thức (7) được sử dụng thực tế khi hàm tự hiệp phương sai thực, y(0) và y(ts) đã biết từ quan trắc nhiễu nền như thế hiện trên Hình 2. Thay thế công thức (7) cho công thức (2) (sY = sDY) sẽ dẫn đến giá trị tối thiểu phát hiện được.
Có thể sử dụng định lý WienerKhintchine [5] liên hệ hàm tự hiệp phương sai với mật độ phổ công suất thông qua biến đổi chuỗi Fourier:
![]() (8)
(8)
trong đó
Sb(f) ký hiệu cho phổ công suất của nhiễu nền quan trắc được;
G(f) là đáp ứng tần số của hệ thống chỉ thị (tuyến tính).
Công thức (8) chỉ ra ước lượng của phép đo SD, Công thức (7), thông qua phổ công suất nhiễu.
5.2. Lý thuyết dựa trên phổ công suất
Lý thuyết dựa trên phổ công suất của đường cơ sở, được gọi là FUMI (hàm thông tin tương hỗ) [6][7][8], đưa ra giá trị SD của diện tích và độ cao đo được trong phân tích bằng dụng cụ. Các giá trị đo được này là tích hợp của đầu ra phương tiện đo trong vùng tích hợp, như minh họa trên Hình 3. Nếu tín hiệu (hình dạng và cỡ) không thay đổi, thì sai số diện tích hay độ cao đo được, miễn là nó xuất phát từ riêng nhiễu, sẽ bằng diện tích tạo bởi nhiễu trong vùng tích hợp đó. Nghĩa là, sai số đo giống như với phần diện tích tạo bởi nhiễu. SD của diện tích tạo bởi nhiễu trùng với SD của độ cao hoặc diện tích đo được.
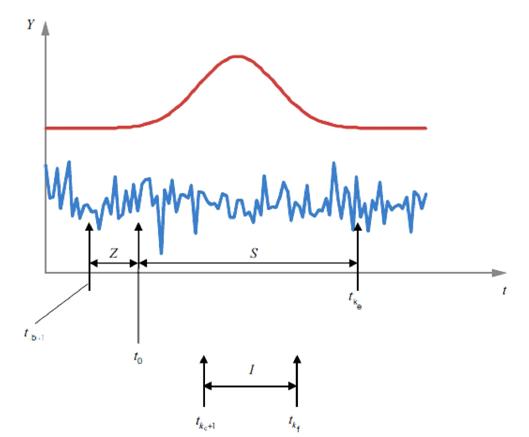
CHÚ DẪN
Z cửa sổ “không”
S vùng tín hiệu
I vùng tích hợp
(Các ký hiệu bổ sung được giải thích trong Phụ lục A.)
Hình 3 – Tín hiệu và nhiễu với cửa sổ “không” và diện tích tích hợp
Số điểm dữ liệu trong vùng tích hợp là kf – kc.
Trong lý thuyết FUMI, cường độ nhiễu, Yi, tại điểm i được mô tả như các quá trình ngẫu nhiên pha trộn của nhiễu trắng và quá trình Markov:
Yi = wi + Mi (9)
Mục đích của lý thuyết FUMI là để ước lượng SD của diện tích tạo bởi nhiễu, AF, trong vùng tích hợp (xem Hình 3).
Trên thực tế, đặc biệt là phép sắc ký, các phương thức tích hợp khác nhau được lựa chọn như minh họa trên Hình 4. Phép đo là đo các cường độ tích hợp phía trên đường cơ sở, nằm ngang hoặc nghiêng trong miền [kc + 1, kf]. Đường cơ sở nằm ngang được vẽ theo phương ngang từ cường độ (được hiệu chính) tại điểm “không”, còn đường nghiêng được vẽ giữa các cường độ tại các mép của vùng tín hiệu [0, ke]. Đường nghiêng thường hữu ích đối với nhiễu nền thay đổi chậm, gọi là “độ trôi” trong phép sắc ký.
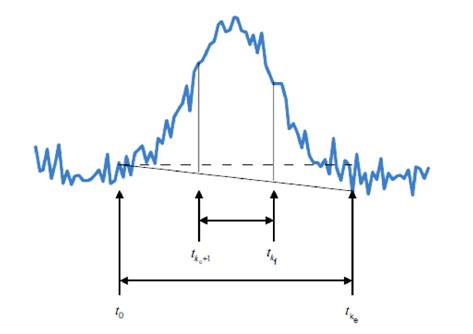
Hình 4 – Phương thức tích hợp trên đường nằm ngang (đường đứt nét) và đường nghiêng (đường liền nét) giữa ![]() và
và ![]()
Diện tích tạo bởi nhiễu, là diện tích giữa tuyến ngẫu nhiên và đường nằm ngang trong vùng tích hợp không có tín hiệu, có thể được viết là:
![]() (10)
(10)
trong đó cường độ nhiễu, Yi, được mô tả bằng công thức (9) và Dt là khoảng thời gian giữa các dữ liệu liên tiếp. Ở đây AF nghĩa là biến đáp ứng Y.
Nếu sử dụng đường nghiêng làm đường cơ sở thì diện tích tạo bởi nhiễu có dạng:
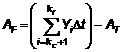 (11)
(11)
trong đó AT ký hiệu cho diện tích hình thang tạo bởi đường nghiêng, đường nằm ngang và đường thẳng tại các mép của vùng tích hợp từ kc + 1 đến kf (xem Hình 4). Diện tích của hình thang trên Hình 4 được lấy dấu âm. Diện tích này lấy dấu dương nếu đường nghiêng nằm phía trên đường nằm ngang trong vùng tích hợp còn nếu không sẽ mang dấu âm.
Biểu thức tổng quát của SD, sF, của diện tích tạo bởi nhiễu là:
sF = (E[AF2]1/2 (12)
trong đó E[×] ký hiệu cho trung bình chung của biến ngẫu nhiên trong ngoặc vuông. Cần lưu ý là E[AF] = 0 vì theo định nghĩa, trung bình chung của diện tích tạo bởi nhiễu trên đường nằm ngang [số hạng thứ nhất ở vế phải của công thức (11)] bằng “không” và trung bình chung của hình thang, AT, bằng “không” (xem thêm Phụ lục C).
Suy luận trên đây dựa vào giả định là không có độ không đảm bảo của mức “không”, nghĩa là Y0 = 0. Tuy nhiên, trên thực tế, vẫn có loại độ không đảm bảo này và cần được tính đến. Phép đo trong phép sắc ký thường được thực hiện tương ứng với mức “không”, là trung bình các cường độ nhiễu nền trong vùng mà ở đây gọi là cửa sổ “không” (xem Hình 3).
SD bình phương, ![]() , của diện tích đo được (diện tích tạo bởi nhiễu) trong vùng cửa sổ “không” có dạng[6][7][8]:
, của diện tích đo được (diện tích tạo bởi nhiễu) trong vùng cửa sổ “không” có dạng[6][7][8]:
![]() (13)
(13)
trong đó ![]() ký hiệu cho phương sai bắt nguồn từ cửa sổ “không” và
ký hiệu cho phương sai bắt nguồn từ cửa sổ “không” và ![]() là phương sai từ diện tích đo được [sF cho bởi công thức (12)]. Tổng hợp về dẫn xuất của công thức (14) và (15) được cho trong Phụ lục C. Giá trị tối thiểu phát hiện được có thể thu được bằng cách thay thế công thức (13) cho công thức (2).
là phương sai từ diện tích đo được [sF cho bởi công thức (12)]. Tổng hợp về dẫn xuất của công thức (14) và (15) được cho trong Phụ lục C. Giá trị tối thiểu phát hiện được có thể thu được bằng cách thay thế công thức (13) cho công thức (2).
Phương sai, ![]() , có thể được mô tả là [6][7][8]:
, có thể được mô tả là [6][7][8]:
![]() (14)
(14)
và ảnh hưởng của tích hợp tín hiệu trong vùng tín hiệu có dạng: [6][7][8]
![]() (số hạng thứ nhất)
(số hạng thứ nhất)
![]() (số hạng thứ hai)
(số hạng thứ hai)
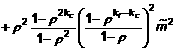 (số hạng thứ ba)
(số hạng thứ ba)
![]() (số hạng thứ tư)
(số hạng thứ tư)
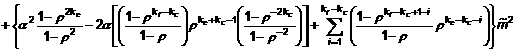 (số hạng thứ năm) (15)
(số hạng thứ năm) (15)
trong đó
![]() (16)
(16)
![]() ký hiệu cho SD của nhiễu trắng;
ký hiệu cho SD của nhiễu trắng;
![]() là SD của nhiễu trắng bao gồm trong quá trình Markov;
là SD của nhiễu trắng bao gồm trong quá trình Markov;
r là tham số không đổi của quá trình Markov;
kc, kf và ke được xác định trên Hình 3 và Hình 4;
b ký hiệu cho số điểm dữ liệu liên tục trong cửa sổ “không” [-b + 1, 0].
Năm số hạng trong công thức (15) ký hiệu cho các đóng góp ngẫu nhiên sau đây vào độ không đảm bảo đo:
– số hạng thứ nhất: sai số từ nhiễu trắng trong miền tích hợp (kf – kc điểm dữ liệu);
– số hạng thứ hai: sai số từ quá trình Markov trong miền tích hợp (kf – kc điểm dữ liệu);
– số hạng thứ ba: ảnh hưởng của kc điểm dữ liệu giữa điểm “không” và điểm bắt đầu tích hợp;
– số hạng thứ tư: ảnh hưởng của nhiễu trắng trong đường cơ sở nghiêng;
– số hạng thứ năm: ảnh hưởng của quá trình Markov trong đường cơ sở nghiêng.
6. Ứng dụng thực tiễn của lý thuyết FUMI
6.1. Ước lượng các tham số nhiễu
Tất cả các tham số cần thiết cho việc áp dụng lý thuyết FUMI, nghĩa là công thức từ (13) đến (16), có thể xác định đơn nhất từ các dữ liệu thực nghiệm. Các tham số tín hiệu (b, kc, kf, ke) có thể thiết lập theo hình dạng của đỉnh mục tiêu, như thể hiện trên Hình 3. Mặt khác, các tham số nhiễu (![]() ) được xác định tự động từ mật độ phổ công suất của nhiễu, như mô tả dưới đây.
) được xác định tự động từ mật độ phổ công suất của nhiễu, như mô tả dưới đây.
Mật độ phổ công suất nhiễu thu được từ biến đổi Fourier các dữ liệu nhiễu, Yi. Fourier và biến đổi nghịch đảo Fourier là
![]() (17)
(17)
![]() (18)
(18)
trong đó
N ký hiệu cho số điểm dữ liệu liên quan trong vùng biến đổi Fourier;
W = exp[-j(2p/ N)];
j là đơn vị ảo.
Mật độ phổ công suất, P(k), của quá trình ngẫu nhiên, Yi, được xác định là
![]() (19)
(19)
trong đó ![]() là số liên hợp của
là số liên hợp của ![]() .
.
Nếu sử dụng mô hình nhiễu mô tả bởi công thức (9), thì mật độ phổ công suất của công thức (19) có thể mô tả là[6][7][8]
![]() (20)
(20)
Các tham số nhiễu (![]() , và r) cần thiết cho lý thuyết FUMI có thể được xác định bằng cách làm khớp bình phương tối thiểu phi tuyến của công thức (20) với mật độ phổ công suất của nhiễu nền thực tế.
, và r) cần thiết cho lý thuyết FUMI có thể được xác định bằng cách làm khớp bình phương tối thiểu phi tuyến của công thức (20) với mật độ phổ công suất của nhiễu nền thực tế.
Số hạng thứ nhất của phép biến đổi Fourier, ![]() , nằm trong công thức (19) và (20) là thành phần dc, và mật độ phổ tương ứng, P(0), được bỏ qua. Tần số, k, trong công thức (20), ở đây là số nguyên, trải từ 1 đến N/2, trong đó N/2 là tần số Nyquyst. Ví dụ điển hình của công thức (20) được minh họa trên Hình 5.
, nằm trong công thức (19) và (20) là thành phần dc, và mật độ phổ tương ứng, P(0), được bỏ qua. Tần số, k, trong công thức (20), ở đây là số nguyên, trải từ 1 đến N/2, trong đó N/2 là tần số Nyquyst. Ví dụ điển hình của công thức (20) được minh họa trên Hình 5.
Trên thực tế, tần số, k, thường được tính bằng Héc. Lấy Dt là khoảng thời gian giữa các điểm dữ liệu liên tục (các khoảng của bộ chuyển đổi tương tự-số dùng cho thu nhận dữ liệu, Yi). Tần số ứng với k (= 1, 2, …, N/2) là k/(Dt N).
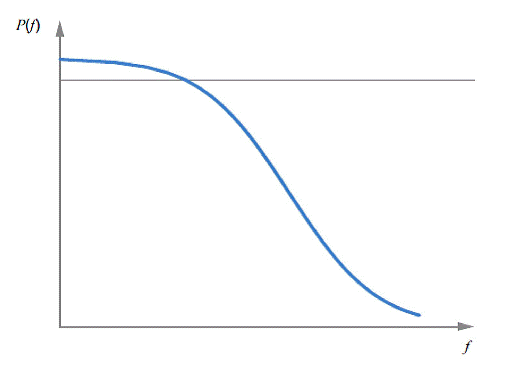
Hình 5 – Mật độ phổ công suất của mô hình nhiễu
Trên thực tế, mật độ phổ công suất sẽ kém trơn hơn trên lý thuyết ở Hình 5. Nếu đó là dạng quan trắc được thì nó có thể có dao động nhỏ quanh tín hiệu trơn.
6.2. Quy trình ước lượng SD
Lý thuyết FUMI đòi hỏi đầu ra của phương tiện đo để ước lượng SD của diện tích đo được, lần lượt sẽ dẫn đến giá trị tối thiểu phát hiện được. Tập hợp hoàn chỉnh các bước được minh họa trên Hình 6.
Đầu ra thiết bị số như máy sắc ký và quang phổ được yêu cầu để tách các tham số tín hiệu và nhiễu. Các tham số tín hiệu liên quan đến vùng tín hiệu trải từ điểm 0 đến điểm ke, vùng tích hợp từ điểm kc+1 đến điểm kf, và cửa sổ “không” từ điểm 0 đến –b + 1 (xem Hình 3). Vùng tín hiệu được tạo bởi ke+1 điểm dữ liệu, vùng tích hợp gồm ke – kc điểm dữ liệu, còn cửa sổ “không” là b điểm dữ liệu.
Các tham số tín hiệu là tùy biến, tuy nhiên chỉ dẫn dưới đây sẽ hữu ích trong thực hành. Đối với tín hiệu Gaussian như trên Hình 3, vùng tín hiệu có thể là ± 3s hoặc ± 4s quanh tâm tín hiệu, trong đó s ký hiệu cho độ lệch chuẩn (độ rộng) và tâm tín hiệu là trung bình của tín hiệu Gaussian (ke = 6s hoặc 8s). Trong nhiều trường hợp, độ cao đỉnh hoặc toàn bộ diện tích là phép đo điển hình. Đối với phép đo độ cao đỉnh, kf = kc + 1. Đối với phép đo toàn bộ diện tích, kf = ke -1 và kc = 0. Ở một trong hai phép đo, số điểm dữ liệu trong vùng tích hợp là kf – kc. Tích hợp trên một phần của vùng tín hiệu, như thể hiện trên Hình 3, cũng có hiệu lực trên quan điểm độ chụm. Cửa sổ “không” có thể thiết lập thực nghiệm là vùng thậm chí hẹp hơn vùng tín hiệu, như thể hiện trên Hình 3.
Không giống như tham số tín hiệu, tham số nhiễu (![]() , và r) được xác định đơn nhất theo các thuộc tính ngẫu nhiên của nhiễu nền. Một số ví dụ trong sắc ký lỏng được cho trong Bảng 1. Bước đầu tiên là xác định vùng không có đóng góp tín hiệu đáng kể trong nhiễu nền.
, và r) được xác định đơn nhất theo các thuộc tính ngẫu nhiên của nhiễu nền. Một số ví dụ trong sắc ký lỏng được cho trong Bảng 1. Bước đầu tiên là xác định vùng không có đóng góp tín hiệu đáng kể trong nhiễu nền.
Bước thứ hai là biến đổi Fourier nhiễu nền trong vùng này để có được mật độ phổ công suất theo công thức (20). Nếu sử dụng số, N, điểm dữ liệu trong công thức (20) giới hạn ở lũy thừa bậc n của 2 trong biến đổi Fourier nhanh (FFT) thì 512 hoặc 1 024 điểm dữ liệu sẽ thích hợp cho vùng FFT đối với vùng tín hiệu gồm 50 hoặc 100 điểm dữ liệu.
Bước thứ ba là làm khớp bình phương tối thiểu của đường cong lý thuyết [công thức (20)] với mật độ phổ công suất thu được như đề cập ở trên. Một số ít các điểm dữ liệu trong vùng FFT (ví dụ: 32), trong một số tình huống, có xu hướng chệch với ước lượng đúng của các tham số nhiễu.
Tham số tín hiệu và nhiễu xác định như đề cập ở trên được thay cho công thức (13) đến (16) để cho giá trị cuối cùng của lý thuyết FUMI (độ chụm).
Khả năng áp dụng lý thuyết FUMI tương đối rộng, nhưng có hai tình huống điển hình không áp dụng được.
– Một là nguồn sai số chiếm ưu thế không phải là nhiễu nền. Trong phép khối phổ, nếu quá trình ion hóa tạo ra quá nhiều sai số so với nhiễu thì lý thuyết FUMI sẽ ước lượng quá thấp SD của diện tích đo được.
– Tình huống còn lại là khi nhiễu thiết bị thực tế bao gồm nhiễu không thể xác định gần đúng bằng quá trình phối hợp giữa nhiễu trắng và quá trình Markov. Ví dụ như nhiễu nhọn cường độ cao.
Giá trị tối thiểu phát hiện được có thể tìm trên đồ thị từ biên dạng độ chụm như biến trạng thái tịnh tại đó CV của biến trạng thái tịnh là 30 %. Phương pháp này cũng được áp dụng cho CV của biến đáp ứng, vì biên dạng độ chụm của biến trạng thái tịnh giống như của biến đáp ứng nếu hàm hiệu chuẩn tuyến tính.[9][10] Tuy nhiên, trong trường hợp hiệu chuẩn phi tuyến, biên dạng độ chụm của biến đáp ứng và biến trạng thái tịnh sẽ khác nhau. Trong trường hợp này, phương pháp nêu trong TCVN 10431-
5 (ISO 11843-5) áp dụng cho việc biến đổi các biên dạng độ chụm khác nhau và giá trị tối thiểu phát hiện được cũng có thể ước lượng.
Bảng 1 – Ví dụ về ước lượng tham số nhiễu trong sắc ký lỏng[6]
|
|
|
|
r |
|
Thực nghiệm A |
14 |
3,7 |
0,99 |
|
Thực nghiệm B |
12 |
9,0 |
0,94 |
|
Thực nghiệm C |
14 |
5,6 |
0,99 |
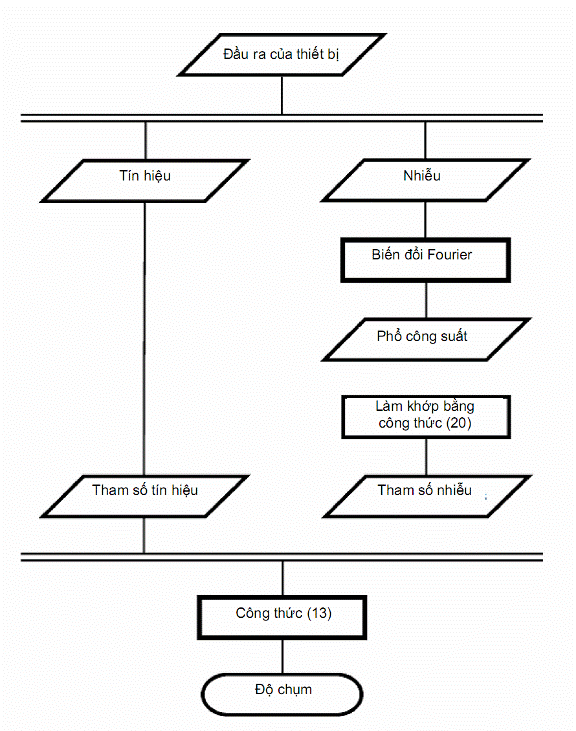
Hình 6 – Các quy trình của lý thuyết FUMI
PHỤ LỤC A
(tham khảo)
Ký hiệu và từ viết tắt sử dụng trong tiêu chuẩn này
SD độ lệch chuẩn
CV hệ số biến động (SD chia cho trung bình)
X biến trạng thái tịnh
Y biến đáp ứng (diện tích hoặc độ cao đo được)
ti một trong tập hợp các giá trị thời gian cách đều nhau t1, t2, …
Dt ti+1 – ti, độ dài khoảng thời gian cho chuyển đổi tương tự-số trong thu thập dữ liệu
Yi cường độ đầu ra thiết bị tại thời điểm ti (tổng của Yi nghĩa là Y)
Yt cường độ đầu ra thiết bị tại thời điểm t (tổng của Yt nghĩa là Y)
xd giá trị tối thiểu phát hiện được của biến trạng thái tịnh
kc hệ số để quy định xác suất sai lầm loại một
kd hệ số để quy định xác suất sai lầm loại hai
sY(X) SD của biến đáp ứng là hàm số của X
sX(X) SD của biến trạng thái tịnh là hàm số của X
½dY/dX½ đạo hàm của hàm hiệu chuẩn
E[×] trung bình của biến ngẫu nhiên trong ngoặc vuông
y(t) hàm tự hiệp phương sai với độ trễ t, xác định bởi công thức (5)
wi biến ngẫu nhiên tại điểm i của nhiễu trắng với trung bình “không” và SD ![]()
![]() SD của nhiễu trắng wi
SD của nhiễu trắng wi
Mi biến ngẫu nhiên của quá trình Markov tại điểm i
mi nhiễu trắng trong quá trình Markov tại điểm i, xác định bởi công thức (4)
![]() SD của nhiễu trắng mi trong quá trình Markov
SD của nhiễu trắng mi trong quá trình Markov
r tỷ số cho duy trì trạng thái trước đó, xác định bởi công thức (4)
AF diện tích tạo bởi nhiễu, là diện tích do riêng nhiễu tạo ra
FUMI từ viết tắt của hàm thông tin tương hỗ
PHỤ LỤC B
(tham khảo)
Dẫn xuất công thức (7)
Phương sai của chênh lệch cường độ giữa các điểm t0 và t0 + ts có thể được viết là:[2-4]
![]() (B.1)
(B.1)
Từ định nghĩa về hàm tự hiệp phương sai [công thức (5)], số hạng thứ hai ở vế phải của công thức (B.1) có thể được mô tả là
y(0) ≡ E [![]() (B.2)
(B.2)
Giả định về tính dừng của dao động nền cân bằng số hạng thứ nhất và thứ hai ở vế phải của công thức (B.1):
![]() (B.3)
(B.3)
Với giả định tính dừng, công thức này nghĩa là phương sai của dao động nền là hằng số không đổi theo thời gian. Khi đó, công thức (B.1) có thể được viết là:
σ∆Y2 = 2y(0) − 2E![]() (B.4)
(B.4)
Chú ý đến định nghĩa về tự hiệp phương sai [công thức (5)], ta có thể thu được công thức (7).
PHỤ LỤC C
(tham khảo)
Dẫn xuất các công thức từ (14) đến (16)
Giả định cơ bản về dẫn xuất của các công thức từ (14) đến (16) là biến ngẫu nhiên của nhiễu trắng độc lập nhau:
E [wiwj] = 0 nếu i ≠ j (C.1)
E [wiwj] = ![]() nếu i = j (C.2)
nếu i = j (C.2)
E [mimj] = 0 nếu i ≠ j (C.3)
E [mimj] = ![]() nếu i = j (C.4)
nếu i = j (C.4)
E [wimj] = 0 = 0 (C.5)
trong đó công thức (C.5) đúng trong mọi điều kiện. Dẫn xuất của công thức trong phụ lục này lấy trường hợp đường cơ sở nghiêng, vì các công thức thu được có thể bao gồm cả trường hợp đường cơ sở nằm ngang.
Độ dốc của đường cơ sở nghiêng đi qua điểm “không” (Y0 = 0) và cường độ tại ke là Yke /ke. Do đó, độ cao của cạnh vùng tích hợp được viết là
![]() tại kc + 1 (C.6)
tại kc + 1 (C.6)
![]() tại kf (C.7)
tại kf (C.7)
trong đó Yi được cho bởi công thức (9). Hình thang tạo bởi đường nghiêng, các đường ngang và dọc (xem Hình 4) có diện tích:
AT = ![]() (C.8)
(C.8)
trong đó a được cho bởi công thức (16). Công thức (11) đối với diện tích tạo bởi nhiễu có dạng:
![]() (C.9)
(C.9)
trong đó Dt của công thức (11) được giả định là như nhau. Phương sai của công thức (C.9) là phương trình mục tiêu [công thức (15)].
Trước khi suy luận, tổng của quá trình Markov được lấy như một ví dụ đơn giản của diện tích đo được. Nếu M0 = 0, thì quá trình Markov xác định bởi công thức (4) còn có dạng:
M1 = m1 (C.10)
M2 = rm1 + m2
…
Mk = rk-1m1 + rk-2m2 + … + rmk-1 + mk (C.12)
Tổng của quá trình Markov có thể viết là:
![]() = (1 + ρ + ρ2 +…+ρk-1)m1 + (1 + ρ + ρ2 +…+ ρk-2)m2 +…+(1+ρ)mk-1 + mk (C.13)
= (1 + ρ + ρ2 +…+ρk-1)m1 + (1 + ρ + ρ2 +…+ ρk-2)m2 +…+(1+ρ)mk-1 + mk (C.13)
Theo định nghĩa, E[mi] = 0, trung bình của công thức (13) là “không”, nhưng phương sai của nó có giá trị hữu hạn:
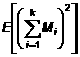 = (1 + ρ + ρ2 +…+ρk-1)2
= (1 + ρ + ρ2 +…+ρk-1)2 ![]() +(1+ ρ + ρ2 +…+ ρk-2)
+(1+ ρ + ρ2 +…+ ρk-2)![]() +…+ (1+ ρ)
+…+ (1+ ρ)![]() +
+![]() (C.14)
(C.14)
Phương trình này có dạng đơn giản là:
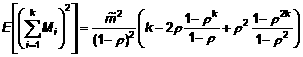 (C.15)
(C.15)
Việc thay thế kf – kc cho k trong công thức (C.15) dẫn đến số hạng thứ hai của công thức (15). Số hạng thứ nhất của công thức (15) là tổng nhiễu trắng trên kf – kc điểm. Các số hạng khác của công thức (15) có thể thu được bằng việc xem xét các công thức từ (C.1) đến (C.5) và (C.9) đến (C.15)[7]. Ngoài ra, E[AF] = 0 với giả định là E[wi] = 0 và E[mi] = 0.
Độ không đảm bảo đi kèm với giá trị đặt mức “không” có thể rút ra theo cách tương tự.[8] Mức “không”, L0, được xác định ở đây là trung bình của b dữ liệu liên tiếp:
![]() (C.16)
(C.16)
trong đó Yi được cho bởi công thức (9). Giá trị đặt mức “không” nghĩa là hiệu chính nền được thực hiện trong toàn bộ vùng tích hợp, tạo ra diện tích dưới đây trong vùng tích hợp:
(kf – kc)L0 (C.17)
Do đó, độ không đảm bảo đi kèm với mức “không” có dạng:
sZ2 = (kf – kc)2 E[L02] (C.18)
trong đó E[L0] = 0 theo định nghĩa. Nếu công thức (C.13) được sử dụng thay cho ![]() trong công thức (C.16) thì công thức thu được ứng với số hạng thứ hai của công thức (14).[8] Số hạng thứ nhất của công thức (14) chỉ chịu ảnh hưởng của nhiễu trắng.
trong công thức (C.16) thì công thức thu được ứng với số hạng thứ hai của công thức (14).[8] Số hạng thứ nhất của công thức (14) chỉ chịu ảnh hưởng của nhiễu trắng.
THƯ MỤC TÀI LIỆU THAM KHẢO
[1] INGLE, J.D.Jr and S.R. CROUCH. Spectrochemical Analysis. Prentice-Hall, Inc., New Jersey, (Phân tích quang phổ hóa học)
[2] ALKEMADE, C.Th.J., W.SNELLEMAN, G.D. BOUTILIER, B.D.POLLARD, J.D. WINEFORDNER, T.L. CHESTER and N. OMENETTO. A review and turorial discussion of noise and signal-to-noise ratios in analytical spectrometry-I. Fundamental principles of signal-to-noise ratios. Spectrochim. Acta, 33B, pp. 383-399, 1978 (Xem xét và thảo luận về nhiễu và tỷ số tín hiệu trên nhiễu trong quang phổ phân tích I. Nguyên tắc cơ bản của tỷ số tín hiệu-nhiễu)
[3] BOUTILIER, G.D., B.D.POLLARD, J.D. WINEFORDNER, T.L. CHESTER and N. OMENETTO. A review and turorial discussion of noise and signal-to-noise ratios in analytical spectrometry-II. Fundamental principles of signal-to-noise ratios. Spectrochim. Acta, 33B, pp. 401-415, 1978 (Xem xét và thảo luận về nhiễu và tỷ số tín hiệu trên nhiễu trong quang phổ phân tích II. Nguyên tắc cơ bản của tỷ số tín hiệu-nhiễu)
[4] ALKEMADE, C.Th.J., W.SNELLEMAN, G.D. BOUTILIER and J.D. WINEFORDNER. A review and turorial discussion of noise and signal-to-noise ratios in analytical spectrometry-III. Multiplicative noises. Spectrochim. Acta, 35B, pp. 261-270, 1980 (Xem xét và thảo luận về nhiễu và tỷ số tín hiệu trên nhiễu trong quang phổ phân tích III. Đa nhiễu)
[5] HINO, M. Spectral Analysis (Supekutoru Kaiseki). Asakura Shoten, Tokyo, 1982 (Phân tích phổ)
[6] HAYASHI, Y. and R.MATSUDA. Deductive prediction of measurement precision from signal and noise in liquyd chromatography. Anal. Chem., 66(18), pp. 2874-2881, 1994 (Dự đoán suy luận độ chụm đo từ tín hiệu và nhiễu trong sắc ký lỏng)
[7] HAYASHI, Y. and R.MATSUDA. Prediction of precision from signal and noise measurement in liquyd chromatography: Mathematical relationship between integration domain and precision, Chromatographia, 41, pp. 75-83, 1995 (Dự đoán độ chụm từ phép đo tín hiệu và nhiễu trong sắc ký lỏng: Quan hệ toán học giữa miền tích hợp và độ chụm)
[8] POE, R.B., HAYASHI, Y. and R.MATSUDA. Precision-optimization of wavelengths in diode-array detection in separation science. Anal. Sci., 13, pp. 951-962, 1997 (Tối ưu hóa độ chụm của bước sóng trong phát hiện chùm diot trong khoa học)
[9] KOTANI, A., Y. YUAN, B. YANG, Y. HAYASHI, R.MATSUDA and F. KUSU. Selection of the optimal solvent grade for the mobile phase in HPLC with electrotechnical detection based on FUMI theory. Anal. Sci., 25, pp. 925-929, 2009 (Lựa chọn cấp dung môi tối ưu cho giai đoạn di động trong HPLC có dò kỹ thuật điện dựa trên lý thuyết FUMI)
[10] KOTANI, A., S. KOJIMA, Y. HAYASHI, R.MATSUDA and F. KUSU. Optimization of capillary liquyd chromatography with electrotechnical detection for determining femtogram levels of baicalin and baicalein on the basis of the FUMI theory. J. Pharm. Biomed. Anal., 48, pp. 780-787, 2008 (Tối ưu hóa sắc ký lỏng mao dẫn có dò kỹ thuật điện để xác định mức femtogram của baicalin và baicalein dựa trên lý thuyết FUMI)
MỤC LỤC
Lời nói đầu
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Thuật ngữ và định nghĩa
4. Phân tích định lượng và nhiễu nền
5. Lý thuyết độ chụm
5.1. Lý thuyết dựa trên hàm tự hiệp phương sai
5.2. Lý thuyết dựa trên phổ công suất
6. Ứng dụng thực tiễn của thuyết FUMI
6.1. Ước lượng các tham số nhiễu
6.2. Quy trình ước lượng SD
Phụ lục A (tham khảo) Ký hiệu và từ viết tắt dùng trong tiêu chuẩn này
Phụ lục B (tham khảo) Dẫn xuất công thức (7)
Phụ lục C (tham khảo) Dẫn xuất các công thức từ (14) đến (16)
Thư mục tài liệu tham khảo


