Tiêu chuẩn Việt Nam TCVN12855-2:2020

TIÊU CHUẨN QUỐC GIA

TCVN 12855-2:2020

ISO/IEC 9796-2:2010

CÔNG NGHỆ THÔNG TIN – CÁC KỸ THUẬT AN TOÀN – LƯỢC ĐỒ CHỮ KÝ SỐ CHO KHÔI PHỤC THÔNG ĐIỆP – PHẦN 2: CÁC CƠ CHẾ DỰA TRÊN PHÂN TÍCH SỐ NGUYÊN

Information technology – Security techniques – Digital signature achemes giving message recovery – Part 2: Integer factorization based mechanisms

 

Lời nói đầu

TCVN 12855-2:2020 hoàn toàn tương đương với ISO/IEC 9796-2:2010.

TCVN 12855-2:2020 (ISO/IEC 9796-2:2010) do Cục Quản lý mật mã dân sự và Kiểm định sản phẩm mật mã biên soạn, Ban Cơ yếu Chính phủ đề nghị, Tổng cục Tiêu chuẩn Đo lường Chất lượng thẩm định, Bộ Khoa học và Công nghệ công bố.

Bộ tiêu chuẩn TCVN 12855:2020 Công nghệ thông tin – Các kỹ thuật an toàn – Lược đồ chữ ký số cho khôi phục thông điệp gồm các tiêu chuẩn sau:

TCVN 12855-2:2020 (ISO/IEC 9796-2:2010), Phần 2: Các cơ chế dựa trên phân tích số nguyên.

TCVN 12855-3:2020 (ISO/IEC 9796-3:2013), Phần 3: Các cơ chế dựa vào logarit rời rạc.

Bộ tiêu chuẩn này có thể có các phần tiếp theo.

 

CÔNG NGHỆ THÔNG TIN – CÁC KỸ THUẬT AN TOÀN – LƯỢC ĐỒ CHỮ KÝ SỐ CHO KHÔI PHỤC THÔNG ĐIỆP – PHẦN 2: CÁC CƠ CHẾ DỰA TRÊN PHÂN TÍCH SỐ NGUYÊN

Information technology – Security techniques – Digital signature schemes giving message recovery – Part 2: Integer factorization based mechanisms

1  Phạm vi áp dụng

Tiêu chuẩn này quy định ba lược đồ chữ ký số cho khôi phục thông điệp, hai trong số đỏ là tất định (không ngẫu nhiên) và một là ngẫu nhiên. Sự an toàn của cả ba lược đồ đều dựa trên độ phức tạp của việc phân tích các số nguyên lớn. Tất cả ba lược đồ đều có thể cung cấp sự khôi phục toàn bộ hoặc một phần thông điệp.

Tiêu chuẩn này quy định phương pháp sản xuất khóa cho ba lược đồ chữ ký. Tuy nhiên, các kỹ thuật quản lý khóa và tạo số ngẫu nhiên (theo yêu cầu của lược đồ chữ ký ngẫu nhiên) nằm ngoài phạm vi của tiêu chuẩn này.

Cơ chế đầu tiên được quy định trong tiêu chuẩn này chỉ áp dụng cho các triển khai hiện có và được giữ lại vì lý do tương thích ngược.

2  Tài liệu viện dẫn

Các tài liệu viện dẫn sau rất cần thiết cho việc áp dụng tiêu chuẩn này. Đối với những tài liệu viện dẫn có năm công bố, thì áp dụng phiên bản được nêu. Đối với tài liệu viện dẫn không ghi năm công bố, thì áp dụng phiên bản mới nhất (bao gồm cả các sửa đổi, bổ sung).

TCVN 11816 (ISO/IEC 10118) (tất cả các phần), Công nghệ thông tin – Các kỹ thuật an toàn – Hàm băm

3  Thuật ngữ và định nghĩa

Tiêu chuẩn này áp dụng các thuật ngữ và định nghĩa sau:

3.1

Khả năng (capacity)

Số nguyên dương chỉ ra số bit có trong chữ ký thuộc phần có thể khôi phục được của thông điệp

3.2

Miền chứng thư (certificate domain)

Tập hợp các thực thể sử dụng các chứng thư khóa công khai được tạo bởi cùng một Cơ quan Chứng thực (CA) hoặc một tập hợp các CA hoạt động theo cùng một chính sách bảo mật

3.3

Các tham số miền chứng thư (certificate domain parameters)

Các tham số mật mã cụ thể cho một miền chứng thư, được biết đến và đồng ý bởi tất cả các thành viên trong miền chứng thư

3.4

Hàm băm kháng va chạm (collision-resistant hash-function)

Hàm băm thỏa mãn tính chất sau đây:

Không thể tính toán để tìm được hai giá trị đầu vào khác nhau mà ánh xạ đến cùng một đầu ra

[TCVN 11816 (ISO/IEC 10118-1)]

3.5

Mã băm (hash-code)

Xâu bit giá trị đầu ra của hàm băm

[TCVN 11816 (ISO/IEC 10118-1)]

3.6

Hàm băm (hash-function)

Hàm ánh xạ các xâu bit thành các xâu có độ dài cố định, thỏa mãn hai tính chất sau đây:

– Với một giá trị đầu ra cho trước, không thể tính toán để tìm được một giá trị đầu vào ánh xạ đến giá trị đầu ra đó;

– Với một giá trị đầu vào cho trước, không thể tính toán để tìm được một giá trị đầu vào khác sao cho ánh xạ đến cùng một giá trị đầu ra

[ISO/IEC 9797-2]

3.7

Hàm tạo mặt nạ (mask generation function)

Hàm ánh xạ các xâu bit thành các xâu bit có độ dài tùy ý, thỏa mãn tính chất sau đây:

– Với một phần cho trước của giá trị đầu ra chứ không phải giá trị đầu vào, không thể tính toán để dự đoán được phần còn lại của giá trị đầu ra

3.8

Thông điệp (message)

Xâu bit có độ dài bất kỳ

[TCVN 12214-1]

3.9

Giá trị đại diện của thông điệp (message representative)

Xâu bit được lấy từ một hàm của thông điệp và được kết hợp với khóa chữ ký bí mật để thu được chữ ký

3.10

Xâu bộ bốn (nibble)

Khối bốn bit liên tiếp nhau (một nửa xâu bộ tám)

3.11

Phần không thể khôi phục (non-recoverable part)

Phần của thông điệp được lưu trữ hoặc được truyền cùng với chữ ký; là rỗng khi thông điệp được khôi phục toàn bộ

3.12

Xâu bộ tám (octet)

Xâu tám bit

3.13

Khóa riêng (private key)

Khóa trong cặp khóa phi đối xứng của một thực thể và chỉ được sử dụng bởi thực thể đó

[TCVN 11817-1]

3.14

Khóa chữ ký riêng (private signature key)

Khóa bí mật định nghĩa phép biến đổi chữ ký bí mật

[TCVN 11817-1]

3.15

Khóa công khai (public key)

Khóa trong cặp khóa phi đối xứng của một thực thể và có thể được công khai

[TCVN 11817-1]

3.16

Hệ thống khóa công khai (public key system)

Lược đồ mật mã <chữ ký số> bao gồm ba hàm số sau đây:

– Sản xuất khóa, phương thức tạo một cặp khóa gồm một khóa chữ ký bí mật và một khóa xác thực công khai;

– Tạo chữ ký, phương thức tạo một chữ ký Σ từ một giá trị đại diện của thông điệp F và một khóa chữ ký bí mật;

– Mở chữ ký, phương thức thu được giá trị đại diện của thông điệp F* từ một chữ ký Σ và một khóa xác thực công khai

CHÚ THÍCH Giá trị đầu ra của hàm này cũng chứa một số chỉ biểu thị thủ tục mở chữ ký đã thành công hay bị lỗi.

3.17

Khóa xác thực công khai (public verification key)

Khóa công khai định nghĩa phép biến đổi xác thực công khai

[TCVN 11817-1]

3.18

Phần có thể khôi phục (recoverable part)

Phần thông điệp được truyền tải bên trong chữ ký

3.19

Salt (Salt)

Mục dữ liệu ngẫu nhiên được tạo ra bởi thực thể ký trong quá trình tạo giá trị đại diện của thông điệp trong Lược đồ chữ ký 2

3.20

Chữ ký (signature)

Xâu bit kết quả của quá trình ký

[TCVN 12214-1]

3.21

Trailer (trailer)

Xâu bit có độ dài một hoặc hai xâu bộ tám, được nối vào cuối phần có thể khôi phục được của thông điệp trong quá trình tạo giá trị đại diện của thông điệp

4  Ký hiệu và chữ viết tắt

Tiêu chuẩn này áp dụng các ký hiệu và chữ viết tắt sau:

CHÚ THÍCH Trong hầu hết các trường hợp, các chữ cái viết hoa được sử dụng để biểu thị các xâu bit và các xâu bộ tám, còn các chữ cái viết thường được sử dụng để biểu thị các hàm số.

C	Độ dài bit xâu mã bộ tám của phần có thể khôi phục được của thông điệp (được sử dụng trong tạo giá trị đại diện của thông điệp trong Lược đồ chữ ký 2 và 3).
c	Năng lực của lược đồ chữ ký, có nghĩa là số lượng bit tối đa sẵn sàng cho phần có thể khôi phục được của thông điệp.
c*	Độ dài thông điệp có thể khôi phục được, có nghĩa là độ dài được tính bằng bit của phần có thể khôi phục được của thông điệp (c≥c*).
D, D’	Các xâu bit được tạo ra trong quá trình tạo giá trị đại diện của thông điệp trong Lược đồ chữ ký 2 và 3.
D*, D’*	Các xâu bit được tạo ra trong lúc khôi phục thông điệp trong Lược đồ chữ ký 2 và 3.
F	Giá trị đại diện của thông điệp (một xâu bit).
F*	Giá trị đại diện của thông điệp đã được khôi phục (giá trị đầu ra của bước mở chữ ký).
g	Hàm tạo mặt nạ.
H	Mã băm được tính toán bằng một hàm của thông điệp M (một xâu bit).
H*	Mã băm đã được khôi phục bằng cách lấy từ việc khôi phục thông điệp
h	Hàm băm kháng va chạm
k	Độ dài bit của các mô-đun của khóa chữ ký bí mật và khóa xác thực công khai (xem Phụ Lục A).
Lh	Độ dài bit của mã băm được tạo ra bởi hàm băm h.
Ls	Độ dài bit của salt S.
M	Thông điệp để ký (một xâu bit).
M*	Thông điệp đã được khôi phục từ chữ ký là kết quả của quá trình xác thực.
M1	Phần có thể khôi phục của thông điệp M, có nghĩa là M = M1 || M2.
M1*	Phần có thể khôi phục đã được khôi phục của thông điệp (được tạo ra trong quá trình khôi phục thông điệp).
M2	Phần không thể khôi phục của thông điệp M, có nghĩa là M = M1 || M2.
M2*	Phần không thể khôi phục của thông điệp, là đầu vào của quá trình xác thực.
N	Xâu bit được xây dựng trong tạo giá trị đại diện của thông điệp trong Lược đồ chữ ký 2
N*	Xâu bit được tạo ra trong quá trình khôi phục thông điệp trong Lược đồ chữ ký 2 và 3.
P	Một xâu các bit 0 được xây dựng trong tạo giá trị đại diện của thông điệp trong Lược đồ chữ ký 2 và 3.
S	Salt (một xâu bit).
S*	Salt đã được khôi phục (một xâu bit).
t	Số xâu bộ tám trong trường Trailer (t = 1 hoặc 2).
T	Trường Trailer (một xâu có độ dài 8t bit được sử dụng trong tạo giá trị đại diện của thông điệp).
Δ	Số nguyên trong khoảng từ 0 đến 7 được sử dụng trong đặc tả phân bổ thông điệp.
δ	Số nguyên trong khoảng từ 0 đến 7 được sử dụng trong đặc tả của Lược đồ chữ ký 2 và 3.
Σ	Chữ ký (một xâu bit chứa k-1 hoặc k bit).
|A|	Độ dài bit của xâu bit A, nghĩa là số bit trong A.
A || B	Phép ghép nối xâu bit A và B (theo thứ tự đó).
éaù	Đối với một số thực a, số nguyên nhỏ nhất không nhỏ hơn a.
a mod n	Đối với các số nguyên a và n, (a mod n) biểu thị số dư (không âm) thu được khi chia a cho n. Một cách tương đương nếu b = a mod n, thì b là số nguyên duy nhất thỏa mãn: (i) 0 ≤ b < n, và (ii) (b-a) là bội số nguyên của n.
Å	Toán tử XOR thực hiện trên bit, được sử dụng để kết hợp hai xâu nhị phân có cùng độ dài.

5  Sự chuyển đổi giữa các xâu bit và số nguyên

Để biểu diễn một số nguyên không âm x dưới dạng một xâu bit có độ dài bằng l (l phải thỏa mãn 2^t > x), số nguyên sẽ được viết lại dưới dạng biểu thức nhị phân duy nhất:

Trong đó 0 ≤ x_i ≤ 2 (lưu ý rằng một hoặc vài chữ số đầu có thể bằng 0 nếu x < 2^l-1. Xâu bit sẽ là x_l-1x_l-2…x₀.

Để biểu diễn một xâu bit x_l-1x_l-2…x₀ (có độ dài l) thành một số nguyên x, quá trình đảo ngược sẽ như sau, x sẽ là số nguyên được định nghĩa bởi công thức

6  Yêu cầu

Người sử dụng tiêu chuẩn này, nếu có thể, được khuyến nghị áp dụng cơ chế thứ hai (Lược đồ chữ ký số 2). Tuy nhiên, trong các môi trường mà việc tạo ra các biến ngẫu nhiên bởi người ký được coi là không khả thi, thì Lược đồ chữ ký số 3 được khuyến nghị sử dụng.

Người sử dụng muốn dùng cơ chế chữ ký số theo tiêu chuẩn này phải đảm bảo các thuộc tính sau đây được thỏa mãn:

a) Thông điệp M để ký là một chuỗi nhị phân có độ dài bất kỳ, có thể rỗng.

b) Hàm ký sử dụng khóa chữ ký bí mật, trong khi hàm xác thực sử dụng khóa xác thực công khai tương ứng.

– Mỗi thực thể ký sẽ sử dụng và giữ bí mật khóa chữ ký bí mật của mình tương ứng với khóa xác thực công khai.

– Mỗi thực thể xác thực phải biết khóa xác thực công khai của thực thể ký.

c) Việc sử dụng các lược đồ chữ ký được quy định trong tiêu chuẩn này đòi hỏi phải lựa chọn một hàm băm kháng va chạm h. Hàm băm được tiêu chuẩn hóa theo TCVN 11816. Sẽ có một ràng buộc giữa cơ chế ký và hàm băm trong khi sử dụng. Nếu không có ràng buộc này, kẻ thù có thể yêu cầu sử dụng một hàm băm yếu (chứ không phải là một hàm băm thực) và từ đó giả mạo chữ ký.

CHÚ THÍCH 1 Có nhiều cách để thực hiện điều kiện này. Các tùy chọn sau được liệt kê theo thứ tự tăng dần của rủi ro.

1. Yêu cầu một hàm băm cụ thể khi sử dụng một cơ chế ký cụ thể. Quá trình xác minh sẽ chỉ sử dụng hàm băm cụ thể đó. TCVN 12214-3 cung cấp một ví dụ về tùy chọn này khi cơ chế DSA yêu cầu sử dụng chức hàm băm chuyên dụng 3 theo TCVN 11816-3 (TCVN 11816-3) (còn gọi là SHA-1).

2. Cho phép tập hợp các hàm băm và chỉ định hàm băm được sử dụng trong các tham số miền chứng thư. Trong miền chứng thư này, quá trình xác minh sẽ sử dụng hàm băm được chỉ định trong chứng thư. Bên ngoài miền chứng thư này, rủi ro có thể phát sinh từ các cơ quan chứng thực (CA) không tuân thủ chính sách của người dùng. Nếu, ví dụ, một CA bên ngoài tạo ra một chứng thư số cho phép các hàm băm khác, thì các vấn đề giả mạo chữ ký có thể phát sinh. Trong trường hợp như vậy, một bên xác thực nhầm lẫn có thể đang tranh chấp với CA tạo ra chứng thư số khác.

3. Cho phép một tập hợp các hàm băm và chỉ định hàm băm được sử dụng bằng một số phương pháp khác, ví dụ như một số chỉ biểu thị trong thông điệp hoặc thỏa thuận song phương. Quá trình xác thực sẽ chỉ sử dụng hàm băm được chỉ ra bằng phương pháp khác này. Tuy nhiên, vẫn có nguy cơ kẻ thù có thể giả mạo chữ ký bằng cách sử dụng một hàm băm khác.

CHÚ THÍCH 2 Phương pháp khác được đề cập đến trong đoạn 3 ngay phía trên có thể dưới dạng một số mã nhận dạng hàm băm có trong giá trị đại diện của thông điệp F (xem mục 8.2.2 và 9.2.3). Nếu mã nhận dạng hàm băm được bao gồm trong F theo cách này thì kẻ tấn công không thể sử dụng lại một chữ ký hiện có với cùng M₁ và một M₂ khác, ngay cả khi bên xác thực có thể bị thuyết phục chấp nhận chữ ký được tạo ra bằng cách sử dụng một hàm băm đủ yếu mà có thể tìm được tiền ảnh. Tuy nhiên, như đã thảo luận chi tiết trong [16] (xem phụ lục D), trong trường hợp này và sử dụng hàm băm yếu, kẻ tấn công vẫn có thể tìm thấy một chữ ký mới với một M₁ “ngẫu nhiên”.

CHÚ THÍCH 3 Cuộc tấn công được đề cập trong CHÚ THÍCH 2 thu được một chữ ký mới với M₁ ‘ngẫu nhiên’ có thể được ngăn chặn bằng cách yêu cầu sự tồn tại của một cấu trúc cụ thể trong M₁. Chẳng hạn như, có thể áp đặt một giới hạn độ dài cho M₁ đủ nhỏ hơn năng lực của lược đồ chữ ký (xem thêm ở Phụ lục D). Đối với các lược đồ chữ ký số 2 và 3, giới hạn độ dài cho M₁ cũng có thể ngăn chặn kẻ tấn công sử dụng lại các chữ ký hiện có ngay cả khi không có mã nhận dạng hàm băm được đưa vào trong giá trị đại diện của thông điệp, với điều kiện hàm tạo mặt nạ g dựa trên hàm băm. Điều này được dựa trên giả định hợp lý rằng hàm băm yếu là một hàm băm “mục đích chung” chứ không phải là một hàm băm được thiết kế chỉ nhằm mục đích giả mạo chữ ký.

Người sử dụng một cơ chế chữ ký số cần tiến hành một đánh giá rủi ro xem xét chi phí và lợi ích của các phương tiện thay thế khác nhau để đạt được điều kiện bắt buộc. Đánh giá này phải bao gồm một đánh giá về chi phí kết hợp với khả năng có một chữ ký giả mạo đang được sản xuất.

d) Bên xác thực chữ ký sẽ luôn luôn có một phương thức độc lập an toàn để xác định lược đồ nào trong ba lược đồ chữ ký được quy định trong tiêu chuẩn này đã được sử dụng để tạo ra chữ ký. Ngoài ra, nếu sử dụng Lược đồ chữ ký số 2 hoặc 3, bên xác thực chữ ký cũng phải có phương thức để xác định hàm tạo chữ ký nào trong hai hàm tạo chữ ký trong Phụ lục B đã được sử dụng. Điều này có thể thu được bằng cách quy định cơ chế và hàm tạo chữ ký trong ‘các tham số miền’ đã được đồng ý hoặc bằng cách đưa ra một mã nhận dạng rõ ràng cho lược đồ chữ ký và hàm tạo chữ ký trong chứng thư khóa công khai của người ký. Hàm tạo chữ ký cũng có thể được quy định trong một mã nhận dạng thuật toán liên kết với dữ liệu đã được ký.

e) Mỗi lược đồ chữ ký số được quy định trong tiêu chuẩn này đều có các tùy chọn cụ thể, phạm vi tùy chọn có thể của người ký phải được biết đến bởi bên xác thực bằng một phương thức độc lập an toàn. Các tùy chọn này bao gồm.

– Đối với tất cả ba lược đồ chữ ký số, bên xác thực phải biết xem trường trailer tùy chọn 1 hoặc 2 có đang làm việc hay không.

– Đối với lược đồ chữ ký số 2 và 3, bên xác thực phải biết L_s, độ dài của salt S.

Ví dụ, điều này có thể thu được bằng cách quy định lựa chọn tùy chọn trong “các tham số miền” hoặc bao gồm thông tin tùy chọn trong chứng thư khóa công khai của người ký.

7  Mô hình quá trình ký và xác thực

7.1  Tổng quan

Mô hình cho một lược đồ chữ ký cho khôi phục thông điệp được trình bày ở đây áp dụng cho cả ba lược đồ trong tiêu chuẩn. Khi được áp dụng cho một thông điệp M, một lược đồ chữ ký kiểu này có thể cung cấp khôi phục hoặc toàn bộ hoặc một phần thông điệp.

– Nếu M là đủ ngắn, thì có thể khôi phục toàn bộ thông điệp vì có thể M được bao gồm toàn bộ trong chữ ký.

– Nếu M quá dài, thì có thể phục hồi thông điệp sẽ một phần. Trong trường hợp này, M sẽ được chia thành phần thể khôi phục được, một xâu bit có độ dài giới hạn được bao gồm trong chữ ký, và phần không thể khôi phục được, một xâu các xâu bộ tám có độ dài bất kỳ được lưu trữ và l hoặc được truyền cùng với chữ ký.

Mô hình được chia thành ba phần: đặc tả thủ tục ký thông điệp, đặc tả thủ tục xác thực chữ ký và chi tiết của các khía cạnh bổ sung của ký và xác thực cần được định nghĩa để hoàn chỉnh đặc tả của một lược đồ chữ ký. Các điều 8, 9 và 10 quy định các khía cạnh bổ sung này cho ba lược đồ được định nghĩa trong tiêu chuẩn này.

7.2  Ký thông điệp

7.2.1  Giới thiệu

Cho một thông điệp M được ký, cần phải thực hiện ba bước để tạo ra một chữ ký trên M, cụ thể là phân bổ thông điệp, tạo xâu có thể khôi phục được và tạo chữ ký.

– Phân bổ thông điệp bao gồm quá trình trong đó thông điệp được chia thành hai phần: phần có thể khôi phục được M₁ và phần không thể khôi phục M₂ (có thể rỗng). Độ dài của phần có thể khôi phục được được giới hạn trên bằng năng lực c của lược đồ chữ ký, một giá trị được xác định bởi việc lựa chọn lược đồ chữ ký và khóa của lược đồ. Phần có thể khôi phục sẽ được khôi phục từ chữ ký trong quá trình xác thực, trong khi phần không thể khôi phục phải được cung cấp cho bên xác thực bằng các phương thức khác (ví dụ nó có thể được gửi hoặc lưu trữ với chữ ký). Do đó, nếu thông điệp đủ ngắn, toàn bộ thông điệp có thể được phân bổ vào phần có thể khôi phục được, và phần không thể khôi phục được sẽ là rỗng.

– Tạo giá trị đại diện của thông điệp lấy đầu vào là hai phần này của thông điệp, và đầu ra là một xâu có định dạng, được gọi là giá trị đại diện của thông điệp, là đầu vào cho bước tạo chữ ký.

– Tạo chữ ký lấy đầu vào là giá trị đại diện của thông điệp và khóa chữ ký bí mật và đầu ra là chữ ký Σ. Quá trình này được thực hiện bằng cách sử dụng một hệ thống khóa công khai.

7.2.2  Phân bổ thông điệp

Sự lựa chọn lược đồ chữ ký và khóa cho lược đồ xác định năng lực c của chữ ký, trong đó c phải thỏa mãn c ≥ 7. Thông điệp M cần được ký sẽ được chia thành hai phần, M₁ và M₂ như sau.

Một độ dài thông điệp có thể khôi phục được c* sẽ được lựa chọn, trong đó c* ≤ c, c* ≤ |M| và c* = |M| (mod 8) . Đối với Lược đồ chữ ký 1, c* sẽ được thiết lập bằng với giá trị nhỏ nhất của c – Δ và |M|, trong đó Δ = (c – |M|)mod 8.

– Nếu |M| = c* thì toàn bộ thông điệp sẽ có thể khôi phục được, có nghĩa là M₁ = M và M₂ sẽ là rỗng.

– Nếu |M| > c* thì M₁ sẽ được thiết lập bằng với c* bit bên trái nhất của M, và M₂ sẽ được thiết lập bằng với phần còn lại của M, có nghĩa là M₂ chứa |M| – c* bit.

Trong cả hai trường hợp, M = M₁ || M₂.

CHÚ THÍCH 1 Để phục vụ các mục đích thực tiễn, một ứng dụng có thể muốn cấu trúc thông điệp M để đảm bảo rằng dữ liệu mà nó cần được lưu trữ hoặc truyền dưới dạng rõ (ví dụ: thông tin địa chỉ) được phân bổ vào phần thông điệp không thể phục hồi M₂. Tuy nhiên, việc cấu trúc và biểu diễn của thông điệp M là nằm ngoài phạm vi của tiêu chuẩn này.

CHÚ THÍCH 2 Phương thức phân bổ thông điệp đảm bảo rằng M₂ luôn luôn có độ dài là số nguyên lần các xâu bộ tám. Hơn nữa, chọn c* là giá trị nhỏ nhất của c – Δ và |M|, trong đó Δ = (c – |M|)mod8, đảm bảo rằng M₁ càng dài càng tốt do điều kiện này. Ngoài ra, nếu M có độ dài là số nguyên lần các xâu bộ tám, tức là nếu |M| là bội số nguyên của 8, thì cả M₁ và M₂ sẽ bao gồm một số nguyên lần các xâu bộ tám.

7.2.3  Tạo giá trị đại diện của thông điệp

Bước này sẽ lấy đầu vào là phần có thể khôi phục và phần không thể khôi phục của thông điệp, M₁ và M₂, và đầu ra là giá trị đại diện của thông điệp F. Điều này sẽ đạt được bằng cách sử dụng một trong các phương pháp được quy định tại các điều 8, 9 và 10 trong tiêu chuẩn này. Các phương pháp này yêu cầu phải sử dụng hàm băm h, và trong trường hợp các cơ chế thứ hai và thứ ba, một hàm tạo mặt nạ g cũng sử dụng h. Hàm băm h được sử dụng sẽ được lựa chọn trong các hàm băm đã được tiêu chuẩn hóa theo TCVN 11816; hàm tạo mặt nạ g sẽ được thiết lập bằng hàm được quy định tại Phụ lục C trong tiêu chuẩn này.

7.2.4  Tạo chữ ký

Bước này lấy đầu vào là giá trị đại diện của thông điệp và khóa chữ ký bí mật và đầu ra là chữ ký Σ. Điều này sẽ đạt được bằng cách sử dụng hệ thống khóa công khai được quy định trong Phục lục B trong tiêu chuẩn này.

7.3  Xác thực chữ ký

7.3.1  Giới thiệu

Một thông điệp đã được ký bao gồm hoặc chữ ký Σ trong trường hợp khôi phục toàn bộ hoặc phần không thể khôi phục được của thông điệp M₂* cùng với chữ ký Σ trong trường hợp khôi phục một phần. Một chữ ký sẽ được chấp nhận khi và chỉ khi quá trình xác thực thành công.

Cho chữ ký Σ và phần thông không thể khôi phục được M₂*, cần phải thực hiện ba bước sau đây để xác thực Σ và khôi phục M*, cụ thể là mở chữ ký, khôi phục thông điệp và lắp ghép thông điệp.

– Mở chữ ký lấy đầu vào là chữ ký Σ và khóa xác thực công khai và đầu ra là một giá trị đại diện của thông điệp đã được khôi phục F* hoặc trả về báo hiệu việc xác thực đã bị lỗi. Quá trình này được thực hiện bằng cách sử dụng một hệ thống khóa công khai.

– Khôi phục thông điệp lấy đầu vào là giá trị đại diện của thông điệp đã được khôi phục F* và phần không thể khôi phục của thông điệp M₂*, và đầu ra là phần có thể khôi phục (đã được khôi phục) của thông điệp M₁* hoặc trả về báo hiệu việc xác thực đã bị lỗi.

– Lắp ghép thông điệp là quá trình mà thông điệp đã được phục hồi M* được khôi phục từ phần có thể khôi phục (đã được khôi phục) M₁* và phần không thể khôi phục M₂* (có thể rỗng).

7.3.2  Mở chữ ký

Bước này lấy đầu vào là chữ ký Σ và khóa xác thực công khai và đầu ra hoặc là một giá trị đại diện của thông điệp đã được khôi phục F* hoặc là trả về báo hiệu việc xác thực đã bị lỗi. Điều này sẽ đạt được bằng cách sử dụng hệ thống khóa công khai được quy định trong Phục lục B của tiêu chuẩn này.

7.3.3  Khôi phục thông điệp

Bước này lấy đầu vào là giá trị đại diện của thông điệp đã được khôi phục F* và phần không thể khôi phục của thông điệp M₂*, và đầu ra là phần có thể khôi phục (đã được khôi phục) của thông điệp M₁* hoặc trả về báo hiệu việc xác thực đã bị lỗi. Điều này sẽ đạt được bằng cách sử dụng một trong các phương pháp được quy định tại các điều 8, 9 và 10 trong tiêu chuẩn này. Các phương pháp này yêu cầu phải sử dụng hàm băm, và trong trường hợp các cơ chế thứ hai và thứ ba, là một hàm tạo mặt nạ. Hàm băm được sử dụng sẽ được lựa chọn trong các hàm băm đã được tiêu chuẩn hóa theo TCVN 11816; hàm tạo mặt nạ sẽ được thiết lập bằng hàm được quy định tại Phụ lục C trong tiêu chuẩn này.

7.3.4  Lắp ghép thông điệp

Lắp ghép thông điệp là quá trình mà thông điệp đã được phục hồi M* được khôi phục từ phần có thể khôi phục (đã được khôi phục) M₁* và phần không thể khôi phục M₂* (có thể rỗng). Có nghĩa là, thông điệp M* được ghép lại với nhau bằng M* = M₁* || M₂*

7.4  Quy định lược đồ chữ ký

Mục đích của mục 7.4 là định nghĩa các lựa chọn cần được thực hiện để quy định thống nhất các quá trình ký và xác thực được quy định trong tiêu chuẩn này.

a) Các bước phân bổ thông điệp và lắp ghép thông điệp được định nghĩa duy nhất trong tiêu chuẩn này.

b) Phải chọn một trong ba tùy chọn trong các bước tạo giá trị đại diện của thông điệp và khôi phục thông điệp, như được định nghĩa trong các điều 8, 9 và 10 trong tiêu chuẩn này. Bất kỳ lựa chọn nào trong ba lựa chọn này được chọn, một hàm băm cũng phải được chọn trong các hàm băm đã được tiêu chuẩn hóa theo TCVN 11816 tùy thuộc vào điều kiện rằng mã băm đầu ra sẽ chứa ít nhất 160 bit. Trong hai trong số ba trường hợp, một hàm tạo mặt nạ được yêu cầu thêm, và hàm được sử dụng được định nghĩa trong Phụ lục C trong tiêu chuẩn này.

c) Các bước tạo chữ ký và mở chữ ký được định nghĩa duy nhất trong Phụ lục B trong tiêu chuẩn này, sự lựa chọn của khóa chữ ký bí mật được sử dụng trong quá trình tạo chữ ký, và trong trường hợp Lược đồ chữ ký 2 và 3 với số mũ lẻ, sự lựa chọn giữa chữ ký cơ sở và thay thế và các hàm xác thực. Phương pháp được sử dụng để tạo ra các cặp khóa chữ ký bí mật và khóa xác thực công khai được định nghĩa trong Phụ lục B trong tiêu chuẩn này.

8  Lược đồ chữ ký số 1

8.1  Tổng quan

Điều 8 xác định quá trình tạo giá trị đại diện của thông điệp và khôi phục thông điệp cho lược đồ chữ ký số tất định cho phép khôi phục thông điệp.

Do các tấn công có thể xảy ra (xem [5] và [6]), lược đồ này sẽ chỉ được sử dụng trong các môi trường nơi các điều kiện về mặt tính toán đảm bảo rằng kẻ tấn công không thể có được chữ ký trên một số lượng lớn các thông điệp đã được lựa chọn.

CHÚ THÍCH Lược đồ chữ ký số 1 chỉ nên sử dụng trong các môi trường đòi hỏi tính tương thích với các hệ thống được cải đặt theo phiên bản đầu tiên của tiêu chuẩn này (xem [5] và [6]). Tuy nhiên, Lược đồ chữ ký số 1 chỉ tương thích với các hệ thống được cài đặt theo phiên bản đầu tiên của tiêu chuẩn này sử dụng mã băm có độ dài ít nhất 160 bit.

8.2  Tham số

8.2.1  Độ dài theo mô-đun

Khóa chữ ký bí mật đang sử dụng được giả định để có một mô-đun với độ dài là k bit (xem Phụ lục B). Nó xác định cả c, năng lực của chữ ký, và độ dài của F, giá trị đại diện của thông điệp.

8.2.2  Các tùy chọn trường trailer

Trong lược đồ này, trường trailer (được sử dụng như là một phần cấu tạo nên giá trị đại diện của thông điệp) có thể có độ dài là một hoặc hai xâu bộ tám. Trailer sẽ bao gồm t xâu bộ tám (t = 1 hoặc 2), trong đó xâu bộ bốn bên phải nhất luôn luôn bằng giá trị ‘C’ của hệ thập lục phân. Có hai lựa chọn sau đây được cho phép.

– Tùy chọn 1 (t = 1): trailer sẽ bao gồm một xâu bộ tám; xâu bộ tám này sẽ bằng giá trị “BC” của hệ thập lục phân.

– Tùy chọn 2 (t = 2): trailer sẽ bao gồm hai xâu bộ tám liên tiếp; xâu bộ tám bên phải sẽ bằng giá trị “CC” của hệ thập lục phân và xâu bộ tám bên trái sẽ là định danh hàm băm. Định danh hàm băm xác định hàm băm đang được sử dụng.

Khoảng từ “00” đến “7F” được dành cho tiêu chuẩn ISO / IEC JTC1; TCVN 11816 quy định một định danh duy nhất trong dải đó cho mỗi hàm băm đã được tiêu chuẩn hóa. Khoảng từ “80” đến “FF” được dành riêng cho việc sử dụng độc quyền.

CHÚ THÍCH Việc sử dụng tùy chọn thứ hai cần bên xác thực phải có một phương tiện độc lập an toàn để biết được hàm băm nào được sử dụng để xác minh chữ ký. Mặc dù điều này trước đây được cho là tùy trường hợp, tuy nhiên nó đã được chứng minh là sai, [16] (xem thêm Phụ lục D).

8.2.3  Năng lực

Năng lực c của chữ ký trong lược đồ này được xác định bởi

c = k – L_h – 8t – 4.

Như đã được định nghĩa trong mục 7.2.2, độ dài c* của thông điệp có thể khôi phục được phải thỏa mãn:

a) c* = |M₁| trong trường hợp khôi phục thông điệp hoàn toàn;

b) c – 7 ≤ c* ≤ c trong trường hợp khôi phục một phần.

8.3  Tạo giá trị đại diện của thông điệp

Trong lược đồ này, việc tạo giá trị đại diện của thông điệp bao gồm hai bước chính:

– Băm thông điệp;

– Định dạng.

8.3.1  Băm thông điệp

Thông điệp M (trong đó M = M₁ || M₂) sẽ là đầu vào của hàm băm h để thu được mã băm H, có nghĩa là, H = h(M). CHÚ THÍCH rằng H chứa L_h bit.

8.3.2  Định dạng

Một xâu có độ dài k bit sẽ được xây dựng như sau (thực hiện từ trái sang phải):

– Hai bit được thiết lập bằng “01”

– Một bit được thiết lập bằng ‘0’ trong trường hợp là khôi phục toàn bộ (nghĩa là M = M₁) và ‘1’ trong trường hợp là khôi phục một phần (nghĩa là khi |M₂| > 0),

– k – L_h – |M₁| – 8t – 4 bit đệm tất cả được thiết lập bằng ‘0’,

– Một bit được thiết lập bằng ‘1’ (bit đệm cuối cùng),

– |M₁| bit của M₁,

– L_h bit của H, mã băm,

– 8t bit của trường trailer T.

CHÚ THÍCH 1: Khi khôi phục một phần được cung cấp, M₂ được giữ càng ngắn càng tốt để phù hợp với điều kiện rằng nó sẽ là một số nguyên lần của xâu bộ tám, trong trường hợp này số bit đệm bằng ‘0’ sẽ ít hơn 8.

Giá trị đại diện của thông điệp F sẽ là kết quả của việc xử lý xâu bên trên từ trái sang phải trong các khối bốn bit liên tiếp, có nghĩa là, các xâu bộ bốn, theo các bước dưới đây.

1. Xâu bộ bốn bên trái nhất sẽ giữ nguyên không thay đổi.

2. Nếu xâu bộ bốn bên trái nhất có bit bên phải nhất là ‘0’ thì

a) Tất cả xâu bộ bốn tiếp theo bằng “0000”, nếu có, sẽ được thay bằng một xâu bộ bốn bằng ‘B’ trong hệ thập lục phân; nó là một phần của trường đệm.

b) Xâu bộ bốn tiếp theo đầu tiên không bằng “0000” sẽ được cộng XOR với ‘B’ trong hệ thập lục phân (nghĩa là “1011”); đây là xâu bộ bốn chứa bit đệm cuối cùng.

3. Tất cả các bit tiếp theo sẽ giữ nguyên không thay đổi.

CHÚ THÍCH 2 Điều này có nghĩa là nếu xâu bộ bốn bên trái nhất có bit bên phải nhất được thiết lập là ‘1’ (và do đó không có ‘0’ bit đệm), thì không có thay đổi được thực hiện đối với xâu bit.

4. Bit đầu tiên của xâu kết quả (sẽ luôn bằng ‘0’) sẽ bị xóa, kết quả là F là một xâu có k – 1 bit.

8.4  Khôi phục thông điệp

Như đã được quy định trong Điều 6, bên xác thực phải biết hàm băm h nào đã được sử dụng trong quá trình ký trước đó. Do đó bên xác thực cũng sẽ biết L_h.

Nếu xâu bộ tám bên phải nhất của giá trị đại diện của thông điệp đã được khôi phục F*, một xâu có k – 1 bit, bằng với

– “BC“ của hệ thập lục phân, thì trailer chỉ bao gồm một xâu bộ tám;

– “CC“ của hệ thập lục phân, thì trailer bao gồm hai xâu bộ tám bên phải nhất của F*, trong đó xâu bộ tám bên trái là định danh của hàm băm được sử dụng. Nó sẽ được kiểm tra để xác định xem nó có giống với hàm băm được sử dụng bởi bên xác thực hay không; nếu không thống nhất thì việc xác thực chữ ký sẽ bị lỗi.

Chữ ký Σ sẽ bị từ chối nếu hoặc trailer hoặc định danh hàm băm (nếu có) không thể được hiểu. Ngược lại, quá trình xác thực sẽ tiếp tục.

Chữ ký Σ sẽ bị từ chối nếu bit bên trái nhất của giá trị đại diện của thông điệp đã được khôi phục F* là ‘0’.

Một bit ‘0’ sẽ được nối liền ở đầu bên trái của xâu (kết quả lả một xâu k bit). Xâu này tiếp theo sẽ được xử lý các khối bốn bit liên tiếp từ trái sang phải, nghĩa là các xâu bộ bốn, theo các bước dưới đây.

1. Xâu bộ bốn bên trái nhất sẽ giữ nguyên không thay đổi.

2. Nếu xâu bộ bốn bên trái nhất có bit bên phải nhất là ‘0’ thì

a) Tất cả xâu bộ bốn tiếp theo bằng ‘B’ của hệ thập lục phân, nếu có, là một phần của trường đệm,

b) Xâu bộ bốn tiếp theo đầu tiên không bằng ‘B’ của hệ thập lục phân sẽ là sẽ là số đảo ngược thứ tự với ‘B’ của hệ thập lục phân để lấy lại giá trị ban đầu của xâu bộ bốn này.

3. Tất cả các bit tiếp theo sẽ giữ nguyên không thay đổi.

Vị trí của bit đệm (bên phải nhất) cuối cùng đã được xác định, và do đó đã tính toán được tổng số bit đệm. Bit thứ ba của xâu bộ bốn đầu tiên cũng có thể được xử lý để xác định xem chữ ký cung cấp khôi phục một phần hay toàn bộ. Trong trường hợp khôi phục một phần, chữ ký Σ sẽ bị từ chối nếu có lớn hơn hoặc bằng chín bit đệm (có nghĩa là có lớn hơn hoặc bằng tám bit 0). Ngược lại, quá trình xác thực sẽ tiếp tục.

Tất cả các bit cho đến cuối trường đệm sẽ được loại bỏ từ bên trái của phiên bản đã được chỉnh sửa của F* và trailer một hoặc hai xâu bộ tám sẽ được loại bỏ từ bên phải. Xâu nhị phân còn lại sẽ được chia làm hai phần.

– Mã băm đã được khôi phục H* sẽ bao gồm L_h bit bên phải nhất.

– Phần đã được khôi phục của thông điệp M₁* sẽ bao gồm các bit còn lại bên trái.

Phần thông điệp đã được khôi phục M₁* sẽ được ghép với M₂*, phần không thể khôi phục được của thông điệp, để đưa vào quá trình xác thực và cho hàm băm. Nếu kết quả là giống như H*, có nghĩa là nếu H* = h(M₁* || M₂*), thì chữ ký được chấp nhận và M₁* sẽ được trả về; ngược lại chữ ký sẽ bị từ chối.

9  Lược đồ chữ ký số 2

9.1  Tổng quan

Điều 9 định nghĩa các quá trình tạo giá trị đại diện của thông điệp và khôi phục thông điệp cho lược đồ chữ ký số ngẫu nhiên cho phép khôi phục thông điệp.

CHÚ THÍCH Lược đồ chữ ký số này tương thích với lược đồ đã được biết đến dưới tên gọi là IFSSR được quy định trong IEEE P1363a, [10]. Nó được dựa trên một cách chặt chẽ vào một lược đồ đã được biết đến dưới tên gọi là PSS-R, [3]. Phương thức tạo giá trị đại diện của thông điệp là tương tự như phương thức đã được biết đến dưới tên gọi là EMSR3 trong IEEE P1363a, [10].

9.2  Tham số

9.2.1  Độ dài mô-đun

Khóa chữ ký bí mật khi sử dụng được giả sử là có một độ dài mô-đun là k bit (xem Phụ lục B). Nó xác định cả c, năng lực của chữ ký, và độ dài của F, giá trị đại diện của thông điệp.

9.2.2  Độ dài salt

Độ dài salt L_s sẽ được lựa chọn. L_s sẽ là một số nguyên dương (L_s > 0); là một giá trị điển hình của L_h.

9.2.3  Các tùy chọn trường trailer

Trong lược đồ này, trường trailer (được sử dụng như là một phần cấu tạo nên giá trị đại diện của thông điệp) có thể có độ dài là một hoặc hai xâu bộ tám. Trailer sẽ bao gồm t xâu bộ tám (t = 1 hoặc 2), trong đó xâu bộ bốn bên phải nhất luôn luôn bằng giá trị ‘C’ của hệ thập lục phân. Có hai lựa chọn sau đây được cho phép.

– Tùy chọn 1 (t = 1): trailer sẽ bao gồm một xâu bộ tám; xâu bộ tám này sẽ bằng giá trị “BC” của hệ thập lục phân.

– Tùy chọn 2 (t = 2): trailer sẽ bao gồm hai xâu bộ tám liên tiếp; xâu bộ tám bên phải sẽ bằng giá trị “CC” của hệ thập lục phân và xâu bộ tám bên trái sẽ là định danh hàm băm. Định danh hàm băm xác định hàm băm đang được sử dụng.

Khoảng từ “00” đến “7F” được dành cho tiêu chuẩn ISO / IEC JTC1; TCVN 11816 quy định một định danh duy nhất trong dải đó cho mỗi hàm băm đã được tiêu chuẩn hóa. Khoảng từ “80” đến “FF” được dành riêng cho việc sử dụng độc quyền.

9.2.4  Năng lực

Năng lực c của chữ ký trong lược đồ này được xác định bởi:

c = k – L_h – L_s – 8t – 2.

9.3  Tạo giá trị đại diện của thông điệp

Trong lược đồ này, việc tạo giá trị đại diện của thông điệp bao gồm hai bước chính:

– Băm thông điệp;

– Định dạng.

9.3.1  Băm thông điệp

Mã băm H sẽ được tính như dưới đây hoặc theo một quy trình gồm các bước tương tự.

Chuyển đổi độ dài bit của M₁ hay |M₁| thành một xâu C có độ dài 64 bit sử dụng phép chuyển đổi đã được mô tả trong điều 5.

Tạo ra một xâu bit ngẫu nhiên mới S có độ dài là L_s bit.

Tính mã băm H bằng công thức H = h(C || M₁ || h(M₂) || S). CHÚ THÍCH rằng H chứa L_h bit.

9.3.2  Định dạng

Giá trị đại diện của thông điệp F sẽ được tính toán như dưới đây hoặc theo một quy trình gồm các bước tương tự.

1. Cho P là một xâu bit chứa k + δ – L_h – L_s – |M₁| – 8t – 2 bit ‘0’ trong đó δ = (1 – k)mod 8.

2. Cho xâu bit D được xác định bởi D = P||’1’||M₁||S, trong đó ‘1’ là một bit. Độ dài của D là k + δ –

L_h – 8t – 1 bit.

CHÚ THÍCH : Nếu mã băm có độ dài là bội số của xâu bộ tám thì xâu bit D cũng sẽ có độ dài là bội số của xâu bộ tám.

3. Áp dụng hàm tạo mặt nạ g cho mã băm H để tạo ra một xâu bit N có độ dài k + δ – L_h – 8t – 1 bit.

4. Độ dài của DÅN là k + δ – L_h – 8t – 1 bit. Cho D’ là xâu k – L_h – 8t – 1 bit thu được bằng cách xóa đi δ bit ở bên trái nhất của DÅN.

5. Cho F = D‘||H||T trong đó T là trường trailer 8 bit, F là xâu có độ dài k – 1 bit.

9.4  Khôi phục thông điệp

Nếu xâu bộ tám bên phải nhất của giá trị đại diện của thông điệp đã được khôi phục F*, một xâu có k – 1 bit, bằng với

– “BC” của hệ thập lục phân, thì trailer chỉ bao gồm một xâu bộ tám;

– “CC” của hệ thập lục phân, thì trailer bao gồm hai xâu bộ tám bên phải nhất của F*, trong đó xâu bộ tám bên trái nhất là định danh của hàm băm được sử dụng. Nó sẽ được kiểm tra để xác định xem nó có giống với hàm băm được sử dụng bởi bên xác thực hay không; nếu không thống nhất thì việc xác thực chữ ký sẽ bị lỗi.

Chữ ký Σ sẽ bị từ chối nếu hoặc trailer hoặc định danh hàm băm (nếu có) không thể được hiểu. Ngược lại, quá trình xác thực sẽ tiếp tục.

Phần thông điệp có thể khôi phục được M₁ sau đó sẽ được khôi phục từ đại diện thông điệp F* đã được khôi phục và phần không thể khôi phục được M₂ như dưới đây hoặc bằng một trình tự các bước tương tự.

1. Thêm δ bit ‘0’ vào bên trái nhất của F*.

2. Cho D’* là k + δ – L_h – 8t – 1 bit bên trái nhất của xâu kết quả, và H* là L_h bit tiếp theo.

3. Áp dụng hàm tạo mặt nạ g cho xâu H* để tạo ra một xâu bit N* có độ dài k + δ – L_h – 8t – 1 bit.

4. Cho D* = D‘* Å N*.

5. Thiết lập δ bit bên trái nhất của D* bằng ‘0’.

6. Thực hiện từ bên trái nhất của D*, tìm kiếm bit ‘1’ đầu tiên. Loại bỏ bit này và tất cả các bit ‘0’ ở bên trái của nó, sau đó cho S* là L_s bit bên phải nhất của D*, và M₁* là các bit còn lại của D*. Nếu không có bit ‘1’ đầu tiên thì trả về báo hiệu quá trình xác thực đã bị lỗi và dừng lại.

7. Chuyển đổi độ dài bit của M₁* thành một xâu C có độ dài 64 bit sử dụng phép chuyển đổi đã được mô tả trong điều 5.

8. Nếu H* = h(C||M₁*||h(M₂*)||S*) thì trả về phần thông điệp có thể khôi phục được M₁*. Ngược lại, trả về báo hiệu quá trình xác thực bị lỗi.

10  Lược đồ chữ ký số 3

Điều 10 định nghĩa các quá trình tạo giá trị đại diện của thông điệp và khôi phục thông điệp cho một lược đồ chữ ký số tất định cho phép khôi phục thông điệp.

Lược đồ này giống hệt như lược đồ đã được định nghĩa tại điều 9 ngoại trừ việc S là một giá trị cố định được cho phép có độ dài bằng 0, có nghĩa là L_s ≥ 0 (không giống như điều kiện L_s > 0 được áp dụng trong điều 9). Do đó lược đồ này là tất định và không ngẫu nhiên.

Salt cố định S có thể được người ký lựa chọn. Ngoài ra, nó có thể được quy định như một phần của các tham số miền.

CHÚ THÍCH 1 Độ an toàn của lược đồ này tương đương với mức độ có thể đạt được từ việc sử dụng “băm toàn miền”, [1], [4].

CHÚ THÍCH 2 Lược đồ chữ ký số 3 được xem là nên được sử dụng hơn lược đồ chữ ký số 1 – xem điều 1. Đó là do các lý do sau đây.

– Các lược đồ giống lược đồ chữ ký số 3 có các bằng chứng toán học về độ an toàn (xem [4]). Tuy nhiên, các kỹ thuật chứng minh này không áp dụng cho Lược đồ chữ ký số 1.

– Hai lược đồ có hiệu quả tương đương.

 

Phụ lục A

(quy định)

Mô-đun ASN.1

A.1  Tổng quan

A.2  Sử dụng các định danh đối tượng đi kèm

Mỗi lược đồ chữ ký đều sử dụng một hàm băm, một dãy bao gồm một định danh thuật toán và các tham số liên quan. Do đó, định danh đối tượng của lược đồ chữ ký có thể được đi kèm với một trong các định danh thuật toán hàm băm chuyên dụng được quy định trong ISO/IEC 10118-3 và các tham số liên quan.

Sử dụng ký hiệu giá trị ASN.1 XML, một giá trị có kiểu SignatureWithMessageRecovery sử dụng cơ chế xử lý chữ ký thông thường 1 được định nghĩa trong tiêu chuẩn này và hàm băm SHA-1 được định nghĩa trong ISO/IEC 10118-3 được biểu diễn như sau:

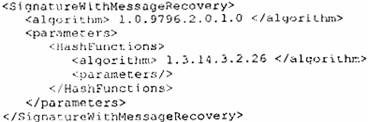
Một giá trị có kiểu SignatureWithMessageRecovery sử dụng định danh đối tượng kết hợp cho cơ chế xử lý chữ ký thông thường 1 và hàm băm SHA-1 có dạng đơn giản như sau:

 

Phụ lục B

(quy định)

Hệ thống khóa công khai cho chữ ký số

Phụ lục này định nghĩa một hệ thống khóa công khai. Hệ thống khóa công khai này bao gồm ba phần chính:

– Tạo khóa, phương pháp tạo một cặp khóa gồm một khóa chữ ký bí mật và một khóa xác thực công khai,

– Tạo chữ ký, phương pháp tạo một chữ ký Σ từ giá trị đại diện của thông điệp F và một khóa chữ ký bí mật, và

– Mở chữ ký, phương pháp thu được giá trị đại diện của thông điệp đã được khôi phục F* từ chữ ký Σ và khóa xác thực công khai. Đầu ra của hàm này cũng chứa một báo hiệu xác định xem thủ tục mở chữ ký đã thành công hay bị lỗi.

B.1  Thuật ngữ và định nghĩa

Trong phụ lục này áp dụng các thuật ngữ và định nghĩa trong tiêu chuẩn này và dưới đây:

B.1.1

Mô-đun

Số nguyên kết quả của việc tạo ra hai số nguyên tố, là thành phần cấu tạo nên các khóa công khai và khóa bí mật

B.1.2

Khóa chữ ký bí mật

Mô-đun và số mũ chữ ký bí mật

B.1.3

Khóa xác thực công khai

Mô-đun và số mũ xác thực công khai

B.2  Ký hiệu và chữ viết tắt

Trong phụ lục này áp dụng các ký hiệu và chữ viết tắt được quy định trong tiêu chuẩn này và dưới đây:

f	Số nguyên với F là biểu diễn nhị phân của nó.
f*	Số nguyên được tính toán trong quá trình mở chữ ký.
J	Số nguyên được tính toán trong quá trình tạo chữ ký.
J*	Số nguyên được tính toán trong quá trình mở chữ ký.
n	Mô-đun (thành phần của khóa chữ ký bí mật và khóa xác thực công khai).
p, q	Các thừa số nguyên tố của mô-đun.
s	Số mũ chữ ký.
v	Số mũ xác thực
lcm(a,b)	Bội số chung nhỏ nhất của số nguyên a và b
min{a,b}	Giá trị nhỏ hơn trong hai giá trị a và b.
(a|n)	Ký hiệu Jacobi của a theo n.

CHÚ THÍCH 1 Cho p là một số nguyên tố lẻ và a là một số nguyên dương. Biểu thức sau định nghĩa ký hiệu Legendre theo p.

(a|p) = a^(p–1)/2mod p.

Ký hiệu Legendre của bội số của p với p bằng 0. Khi a không phải là bội số của p, ký hiệu Legendre của a theo p là +1 hoặc -1 tùy thuộc vào a là hay không là bình phương mô-đun của p.

CHÚ THÍCH 2 Cho n là một số nguyên dương lẻ và a là một số nguyên lẻ. Ký hiệu Jacobi của a theo n là kết quả của ký hiệu Legendre của a theo các phần tử nguyên tố của n (lặp lại ký hiệu Jacobi cho các phần từ nguyên tố đã lập lại). Do đó nếu n = pq, thì (a|n) = (a|p)(a|q). Ký hiệu Jacobi của a theo n vẫn có thể tính được mà không cần biết các phần tử nguyên tố của n.

B.3  Tạo khóa

CHÚ THÍCH Không có một phương pháp về xác thực khóa công khai nào được quy định trong tài liệu này, nó đảm bảo cho một tổ chức (là tổ chức tạo cặp khóa, tổ chức sử dụng khóa công khai hoặc một tổ chức thứ ba trung lập) rằng một khóa công khai nào đó có tuân theo định nghĩa số học của khóa công khai hay không. Một khóa công khai không hợp lệ có thể tồn tại do lỗi tính toán do sơ ý khi tạo khóa hoặc hành động có chủ ý của đối phương. Việc sử dụng một khóa công khai không hợp lệ sẽ chống lại tất cả mọi đảm bảo an toán, bao gồm khả năng đối phương không thể giả mạo một chữ ký hoặc khám phá ra khóa bí mật liên quan. Người sử dụng mong muốn được đảm bảo tính hợp lệ về mặt số học của khóa công khai trước khi sử dụng nó nên sử dụng các phương pháp khác, ví dụ như các phương pháp trong ISO/IEC 9796-3. Là nguyên lý chung của tất cả các hệ thống mật mã, việc sử dụng một khóa công khai hợp lệ nhưng được tạo ra một cách không chính xác (ví dụ như được tạo ra từ một nguồn không đủ ngẫu nhiên), hoặc một khóa bí mật được bảo vệ một cách không chính xác cũng có thể chống lại tất cả mọi đảm bảo an toàn. Kiểm tra tính hợp lệ của các cài đặt có thể giảm thiểu các rủi ro này cũng như khả năng các khóa không hợp lệ được sử dụng. Tuy nhiên, nó không cung cấp sự đảm bảo cụ thể rằng khóa công khai cho trước đó có hợp lệ trên thực tế hay không.

B.3.1  Số mũ xác thực công khai

Mỗi thực thể ký sẽ lựa chọn một số nguyên dương v làm số mũ xác thực công khai, số mũ xác thực công khai này có thể được tiêu chuẩn hóa trong các ứng dụng cụ thể.

CHÚ THÍCH Các giá trị 2, 3, 17 và 65537 có thể có một số ưu điểm về mặt thực tế.

B.3.2  Các thừa số nguyên tố bí mật và số mô đun công khai

Mỗi thực thể ký sẽ lựa chọn một cách bí mật và ngẫu nhiên hai số nguyên tố lớn khác nhau p và q theo các điều kiện sau đây.

– Nếu v là số lẻ, thì p – 1 và q – 1 sẽ là nguyên tố cùng nhau với v.

– Nếu v là số chẵn, thì (p – 1)/2 và (q – 1)/2 sẽ là nguyên tố cùng nhau với v. Hơn nữa, p và q phải không đồng dư với nhau theo mod 8.

Số đồng dư công khai n được thiết lập bằng tích của p và q, có nghĩa là n = pq. Kích thước của n theo bit xác định giá trị của k như sau

2^k-1 < n ≤ 2^k – 1.

CHÚ THÍCH 1 Một số điều kiện bổ sung cho việc lựa chọn số nguyên tố có thể để ngăn chặn việc bị phân tích của mô-đun.

CHÚ THÍCH 2 Một số định dạng của số đồng dư đơn giản hóa việc giảm thiểu mô-đun và yêu cầu ít lưu trữ bảng hơn. Ví dụ của các định dạng này là

n = 2^64x – r của độ dài k = 64x bit,

n = 2^64x + r của độ dài k = 64x + 1 bit,

trong đó: 1 ≤ y ≤ 2x và r < 2^64x–8y < 2r.

Đối với mô-đun có định dạng 2^64x – r, 8y bit quan trọng nhất bằng 1, trong đó 8y nhiều nhất bằng một phần tư độ dài số đồng dư. Đối với mô-đun có định dạng 2^64x + r, bit quan trọng nhất bằng 1 và theo sau nó là 8y bit bằng 0, trong đó 8y nhiều nhất bằng một phần tư độ dài số đồng dư.

B.3.3  Số mũ chữ ký bí mật

Số mũ chữ ký bí mật sẽ là bất kỳ một số nguyên dương s nào sao cho sv – 1 là bội số của

– lcm(p – 1, q – 1) nếu v là số lẻ;

– lcm(p – 1, q – 1)/2 nếu v là số chẵn.

CHÚ THÍCH Nhìn chung, s là giá trị nhỏ nhất có thể.

B.4  Hàm tạo chữ ký

Giá trị đại diện của thông điệp F là một xâu k – 1 bit, trong đó bốn bit bên phải nhất bằng “1100” (‘C’ trong hệ thập lục phân). Nó là biểu diễn nhị phân của một số nguyên dương được ký hiệu là f.

Số nguyên J được định nghĩa như sau:

– nếu v là số lẻ thì J = f,

– nếu v là số chẵn và (f|n) = +1 thì J = f, và

– nếu v là số chẵn và (f|n) = -1 thì J/f/2

CHÚ THÍCH Nếu v là số lẻ thì biểu thức trên đảm bảo rằng ký hiệu Jacobi của J theo n luôn bằng +1.

Chữ ký Σ là một xâu bi có độ dài k – 1 bit tương ứng với số nguyên min{J^smod n,n – (J^smod n)} sử dụng quy ước đã được mô tả trong Điều 5.

B.5  Hàm mở chữ ký

Chữ ký Σ là một xâu k – 1 bit, đó là biểu diễn nhị phân của số nguyên dương nhỏ hơn n. Số nguyên này sẽ tăng lên theo số mũ v mod n để thu được J*, có nghĩa là

J* = Σ^vmod n.

Số nguyên f* sẽ được tính như sau.

– Nếu v là số lẻ và

– nếu J* mod 16 = 12 thì f* = J*,

– nếu J* mod 16 = n – 12 mod 16 thì f* = n – J*.

– Nếu v là số chẵn và

– nếu J* mod 8 = 1 thì f* = n – J*,

– nếu J* mod 8 = 4 thì f* = J*,

– nếu J* mod 8 = 6 thì f* = 2J*,

– nếu J* mod 8 = 7 thì f* = 2(n – J*).

Chữ ký Σ sẽ bị từ chối trong tất cả các trường hợp khác; nó cũng sẽ bị từ chối nếu f* mod 16 ≠ 12, và nếu f* không thỏa mãn f* ≤ 2^k-1 – 1.

Giá trị đại diện của thông điệp đã được khôi phục F* là xâu bit có độ dài k – 1 tương ứng với số nguyên f* sử dụng quy ước đã được mô tả trong Điều 5.

B.6  Hàm tạo chữ ký thay thế

Nếu v là số lẻ thì hàm này có thể được sử dụng như là một sự thay thế cho hàm trong Điều B.4. Nó sẽ được sử dụng cùng với hàm mở chữ ký trong B.7.

Giá trị đại diện của thông điệp F là một xâu k – 1 bit, trong đó bốn bit bên phải nhất bằng “1100” (‘C’ trong hệ thập lục phân). Nó là biểu diễn nhị phân của số nguyên dương được ký hiệu là f.

Số nguyên J được định nghĩa là J = f.

Chữ ký Σ là một xâu bit có độ dài k bit tương ứng với số nguyên J^smod n sử dụng quy ước đã được mô tả trong Điều 5.

CHÚ THÍCH Sự khác nhau giữa hàm này và hàm ở Điều B.4 là chữ ký Σ luôn luôn là J^smod n; không có bước “giá trị tuyệt đối” được thực hiện để lựa chọn giá trị nhỏ hơn giữa J^smod n và n – (J^smod n).

B.7  Hàm mở chữ ký thay thế

Nếu v là số lẻ thì hàm này có thể được sử dụng như là một sự thay thế cho hàm trong Điều B.5. Nó sẽ được sử dụng cùng với hàm tạo chữ ký trong B.6.

Chữ ký Σ là một xâu k bit, đó là biểu diễn nhị phân của số nguyên dương nhỏ hơn n. Số nguyên này sẽ tăng lên theo số mũ v mod n để thu được J*, có nghĩa là

J* = Σ^vmod n.

Số nguyên f* sẽ được tính bằng f* = J*.

Chữ ký Σ sẽ bị từ chối nếu f* mod 16 ≠ 12, và nếu f* không thỏa mãn f* ≤ 2^k-1 – 1.

Giá trị đại diện của thông điệp đã được khôi phục F* là xâu bit có độ dài k – 1 tương ứng với số nguyên f* sử dụng quy ước đã được mô tả trong Điều 5.

CHÚ THÍCH Sự khác nhau giữa hàm này và hàm ở Điều B.5 là số nguyên f* luôn bằng J*; không cần thiết phải “disambiguation” giữa J* và n – J*.

 

Phụ lục C

(quy định)

Hàm tạo mặt nạ

Phụ lục này định nghĩa một hàm tạo mặt nạ dựa trên hàm băm.

CHÚ THÍCH Hàm này là mở rộng của hàm đã được định nghĩa dưới tên gọi là MFG1 trong IEEE Std 1363-2000, cho phép đầu vào đầu ra là các xâu bit. Nó tương tự với đề xuất của Bellare và Rogaway.

Một hàm tạo mặt nạ lấy đầu vào là một xâu bit Z và độ dài mong đợi của đầu ra L_N, và đầu ra là một xâu bit N có độ dài bằng giá trị đó.

C.1  Ký hiệu và chữ viết tắt

Trong phụ lục này cùng với các ký hiệu đã được định nghĩa trong Điều 4, các ký hiệu và chữ viết tắt dưới đây được áp dụng:

L_N         Độ dài (tính bằng bit) của đầu ra của hàm tạo mặt nạ g.

L_Z         Độ dài (tính bằng bit) của xâu bộ tám Z.

N          Đầu ra của hàm tạo mặt nạ g (một xâu bit).

Z          Một xâu bit đầu vào của hàm tạo mặt nạ.

C.2  Yêu cầu

Việc sử dụng hàm này đòi hỏi phải lựa chọn một hàm băm. Hàm băm này, được ký hiệu là h, sẽ được thiết lập bằng hàm băm h như trong đoạn (c) của Điều 6. Chúng ta ký hiệu độ dài đầu ra của h theo bit là L_h.

C.3  Chi tiết kỹ thuật

C.3.1  Tham số

Một đầu vào của hàm g là độ dài mong muốn theo bit của đầu ra, là số nguyên dương L_N.

C.3.2  Tạo mặt nạ

Xâu bit N sẽ được tính toán như sau hoặc theo một trình tự các bước tương tự.

1. Nếu L_z vượt quá giới hạn về độ dài (2⁶⁴ – 33 đối với Hàm băm chuyên dụng 1 và 3 trong ISO/IEC 10118-3), hoặc nếu L_N > L_h x 2³², xuất ra báo “lỗi” và dừng lại.

2. Cho N là một xâu rỗng.

3. Cho i = 0.

3.1  Chuyển đổi i thành một xâu bit C có độ dài 32 bit sử dụng phép chuyển đổi đã được mô tả trong Điều 5.

3.2  Cho N: = N||h(Z||C).

3.3 Cho i: = i + 1.

3.4 Nếu i < éL_N/L_hù, quay lại bước 3.1.

4. Xuất ra L_N bit bên trái nhất của N.

 

Phụ lục D

(tham khảo)

Về định danh hàm băm và sự lựa chọn độ dài có thể khôi phục được của thông điệp

Như được quy định trong Điều 6 (Yêu cầu), người dùng các lược đồ chữ ký được quy định trong tiêu chuẩn này phải lựa chọn một hàm băm kháng va chạm h. Điều quan trọng là bên xác thực có nhiều cách để xác định hàm băm nào đã được sử dụng khi tạo ra chữ ký, để quá trình xác thực có thể diễn ra một cách an toàn. Nếu có một tổ chức thứ ba nguy hiểm có thể thuyết phục bên xác thực rằng một hàm băm “yếu” đã được sử dụng để tạo ra chữ ký (ví dụ như một hàm băm thiếu tính chất một chiều) thì tổ chức thứ ba này có thể thuyết phục bên xác thực rằng một chữ ký có hiệu lực thực sự đã được áp dụng cho một thông điệp “sai”.

Ba lược đồ chữ ký số được quy định trong tiêu chuẩn này cho phép một định danh hàm băm chứa trong giá trị đại diện của thông điệp F (xem 8.2.2). Nếu định danh hàm băm đó chứa trong F theo cách này thì kẻ tấn công không thể sử dụng lại một cách gian lận một chữ ký đã tồn tại với cùng M₁ và khác M₂, thậm chí ngay cả khi bên xác thực có thể bị thuyết phục chấp nhận các chữ ký đã được tạo ra bằng một hàm băm đủ yếu mà tiền ảnh có thể được tìm thấy. Điều này được cho là có thể giải quyết được vấn đề đã được đề cập đến trong đoạn trước.

Tuy nhiên, như đã thảo luận chi tiết trong [16], ngay cả khi một định danh hàm băm được bao gồm trong giá trị đại diện của thông điệp, kẻ tấn công khác đều có thể xảy ra nếu bên xác thực có thể bị thuyết phục bằng một hàm băm “yếu” đã được sử dụng. Từ yếu ở đây có nghĩa là hàm băm thiếu tính chất một chiều, có nghĩa là với một hàm băm cho trước có thể tính toán để tìm ra xâu đầu vào ánh xạ đến mã băm này bởi hàm băm. (CHÚ THÍCH rằng chính xác thì kiểu yếu này trước tiên phải được thúc đẩy bởi sự bao gồm của một định danh hàm băm trong giá trị đại diện của thông điệp.

Các tấn công được mô tả trong [16] hoạt động theo cách thức chung sau đây. Kẻ tấn công tạo ra “chữ ký” ngẫu nhiên và đối với mỗi “chữ ký” này áp dụng một hàm xác thực công khai của thực thể mà chữ ký của nó muốn giả mạo, và thu được “giá trị đại diện của thông điệp đã được khôi phục” (đây là bước “mở chữ ký”). Phần tiếp theo của tấn công sẽ rất khác nhau tùy thuộc vào định dạng của giá trị đại diện của thông điệp, nhưng bắt buộc kẻ tấn công phải xem xét xem giá trị đại diện của thông điệp đã được khôi phục có định dạng đúng tương ứng với chữ ký thật và rằng định danh hàm băm trong xâu này là định danh tương ứng với một hàm băm yếu hay không. Khả năng xảy ra việc này là rất khác nhau, nhưng có thể lớn đến 2^-16 (và do đó kẻ tấn công không cần phải thử quá nhiều “chữ ký ngẫu nhiên” trước khi tìm được một chữ ký có các thuộc tính mong muốn).

Với “chữ ký” này, kẻ tấn công có thể nhúng mã băm vào trong giá trị đại diện của thông điệp đã được khôi phục, và lợi dụng thực tế là hàm băm yếu để phát hiện ra một phần thông điệp không thể khôi phục được, mà khi kết hợp với phần có thể khôi phục được có trong giá trị đại diện của thông điệp, băm để có được mã băm mong muốn. Như thế, kẻ tấn công có thể giả mạo một chữ ký mới với một M₁ “ngẫu nhiên”. Do đó, kể cả khi có định danh hàm băm trong giá trị đại diện của thông điệp cũng không tránh được việc đòi hỏi người xác thực phải có một phương thức độc lập an toàn để biết được hàm băm nào được sử dụng để xác thực chữ ký.

Thảo luận này cũng liên quan đến việc lựa chọn độ dài có thể khôi phục được c* cho lược đồ chữ ký 2 và 3. Như đã được mô tả trong 7.2.2, c* sẽ được lựa chọn thỏa mãn điều kiện c* ≤ c, năng lực của lược đồ chữ ký. c* thường được mong đợi là gần bằng c để tối đa độ dài phần có thể khôi phục được của thông điệp, và do đó tối thiểu độ dài phần không thể khôi phục được của thông điệp, c* được khuyến nghị lựa chọn là một số bất kỳ nhỏ hơn c (ví dụ như c-16, c-24 hoặc c-80, tùy theo độ khó mong muốn), để làm cho các cuộc tấn công theo hình thức đã được mô tả ở trên trở nên khó khăn hơn.

 

Phụ lục E

(tham khảo)

Ví dụ

Phụ lục này bao gồm tổng cộng 12 ví dụ về tạo chữ ký và xác thực chữ ký làm việc theo ba lược đồ đã được quy định trong tiêu chuẩn này, cùng với hai ví dụ về tạo khóa.

Phụ lục E.1 bao gồm các ví dụ với số mũ công khai bằng 3.

– E.1.1 bao gồm một ví dụ về tạo khóa.

– E.1.2 bao gồm ba ví dụ về tạo và xác thực chữ ký, tất cả đều là khôi phục toàn bộ thông điệp. Đối với mỗi lược đồ được quy định trong tiêu chuẩn này có một ví dụ tương ứng.

– E.1.3 bao gồm ba ví dụ về tạo và xác thực chữ ký, tất cả đều là khôi phục một phần thông điệp. Đối với mỗi lược đồ được quy định trong tiêu chuẩn này có một ví dụ tương ứng.

Phụ lục E.2 bao gồm các ví dụ với số mũ công khai bằng 2.

– E.2.1 bao gồm một ví dụ về tạo khóa.

– E.2.2 bao gồm ba ví dụ về tạo và xác thực chữ ký, tất cả đều là khôi phục toàn bộ thông điệp. Đối với mỗi lược đồ được quy định trong tiêu chuẩn này có một ví dụ tương ứng.

– E.2.3 bao gồm ba ví dụ về tạo và xác thực chữ ký, tất cả đều là khôi phục một phần thông điệp. Đối với mỗi lược đồ được quy định trong tiêu chuẩn này có một ví dụ tương ứng

E.1  Các ví dụ với số mũ công khai bằng 3

Phụ lục E.1 bao gồm các ví dụ với khóa công khai có số mũ bằng 3.

E.1.1  Ví dụ về quá trình tạo khóa

Khóa trong ví dụ có mô-đun k = 1024 bit với số mũ công khai v = 3.

Số đồng dư công khai n là kết quả của các thừa số nguyên tố bí mật p và q. Độ dài của nó là 1024 bit.

Số mũ của chữ ký bí mật s bằng nghịch đảo phép nhân của v mod lcm(p – 1, q – 1).

E.1.2  Các ví dụ về khôi phục toàn bộ

Ở đây trình bày ba ví dụ về tạo và xác thực chữ ký, mỗi ví dụ tương ứng với một trong ba lược đồ.

E.1.2.1  Ví dụ về lược đồ chữ ký 1

Ví dụ này sử dụng hàm băm chuyên dụng 3 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là SHA-1).

E.1.2.1.1  Quá trình ký

Thông điệp được ký là một xâu bao gồm 64 ký tự mã ASCII như sau.

Trong hệ thập lục phân, thông điệp M là một xâu có độ dài là 64 xâu bộ tám, nghĩa là 512 bit như sau.

160 bit mã băm được tính toán bằng cách áp dụng SHA-1 cho 512 bit của M.

Định danh trong trường trailer xác định hàm băm được sử dụng; ISO/IEC 10118-3 thiết lập định danh cho hàm băm chuyên dụng 3 giá trị “33”. Do đó, trường trailer 7 bao gồm 16 bit sau đây.

Thông điệp là đủ ngắn để khôi phục toàn bộ. 1024 bit của xâu trung gian S_i kết quả của việc nối hai bit của tiêu đề bằng “01”, bit dữ liệu thêm được thiết lập bằng ‘0’, 332 (= 1024 – 512 – 160 – 16 – 4) bit đệm bằng ‘0’, bit bao quanh bằng 1, 512 bit của M₁ (=M), 160 bit của H và 16 bit của trường trailer T. Xâu S_r có thể khôi phục kết quả của việc thay thế 82 xâu bộ bốn đệm bằng ‘0’ bằng 82 xâu bộ bốn đệm bằng ‘B’ và tương tự đối với xâu bộ bốn bao quanh bằng T thay thế bằng ‘A’.

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. f_r tăng theo lũy thừa bậc s theo mô-đun n. Kết quả được biểu diễn bởi một số nguyên dương không dấu tạm thời t.

Vì kết quả trên lớn hơn n/2, chữ ký Σ = n – t

Thông điệp đã ký có 128 xâu bộ tám chỉ bao gồm chữ ký vì M₂ là rỗng.

E.1.2.1.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. Số nguyên này tăng theo lũy thừa bậc 3 mô-đun n, do đó thu được số nguyên f_s.

Vì f_s là đồng dư với (n – 12) mô-đun 16, nó được thay thế bởi phần dư của nó với n, có nghĩa là số nguyên được khôi phục là f’_r = n – f_s.

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r.

– Xâu bộ tám bên trái nhất của S’_r bằng “4B”; nó bao gồm tiêu đề bằng “01”, bit dữ liệu thêm bằng ‘0’ (khôi phục toàn bộ), một bit đệm bằng ‘0’ và một xâu bộ bốn đệm bằng ‘B’; theo sau là 81 xâu bộ bốn bằng ‘B’ và xâu bộ bốn bao quanh bằng ‘A’; 42 xâu bộ tám này được chuyển sang bên phải của S’_r.

– Xâu bộ tám bên phải nhất của S’_r bằng “CC”; do đó, trailer bao gồm hai xâu bộ tám và bằng “33CC”; hai xâu bộ tám đó cũng được chuyển sang bên phải của S’_r.

Định danh hàm băm bằng “33”; do đó hàm băm được sử dụng là hàm băm chuyên dụng 3.

Xâu còn lại 672 bit được chia làm hai phần.

– M₁* bao gồm 512 bit bên trái nhất.

– H‘ bao gồm 160 bit bên phải nhất.

Thông điệp đã được khôi phục M* chỉ bao gồm M₁* vì khôi phục thông điệp là toàn bộ. Mã băm còn lại H” được tính bằng các áp dụng SHA-1 cho M*.

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

E.1.2.2  Ví dụ về lược đồ chữ ký 2

Ví dụ này sử dụng hàm băm chuyên dụng 1 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là RIPEMD-160).

E.1.2.2.1  Quá trình ký

Trong hệ thập lục phân, thông điệp M là một xâu có độ dài là 48 xâu bộ tám, nghĩa là 384 bit như sau.

160 bit của salt S được tạo ra.

160 bit mã băm được tính toán bằng cách áp dụng hàm băm chuyên dụng 1 để thu được một xâu nhị phân có độ dài là 768 (= 64 + 384 + 160 + 160) và kết quả được ghép thêm 64 bit độ dài thông điệp có thể khôi phục được C, 384 bit của phần có thể khôi phục được M₁ (=M), 160 bit của mã băm của phần không thể khôi phục được (phần này bằng rỗng) h(M₂) và 160 bit của salt S. H = h(C||M₁||h(M₂)||S).

Định danh trong trường trailer xác định hàm băm được sử dụng; ISO/IEC 10118-3 thiết lập định danh cho hàm băm chuyên dụng 1 giá trị “31”. Do đó, trường trailer 7 bao gồm 16 bit sau đây.

Thông điệp là đủ ngắn để khôi phục toàn bộ. 1024 bit của xâu trung gian S_i kết quả của việc nối 303 (= 1024 – 384 – 160 – 160 – 16 – 1) bit đệm bằng ‘0’, bit bao quanh bằng 1, 384 bit của M₁ (=M), 160 bit của L, 160 bit của H và 16 bit của trường trailer T.

Xâu có thể khôi phục S_r thu được từ việc áp dụng hàm tạo mặt nạ MGF1 đối với 848 (= 1024 – 160 – 16) bit bên trái nhất của S_i, và 1 bit bên trái nhất của S_r được thiết lập bằng ‘0’ vì δ = 1 (δ = 1 – 1024)mod 8).

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. f_r tăng theo lũy thừa bậc s theo mô-đun n. Kết quả được biểu diễn bởi một số nguyên dương không dấu tạm thời t.

Xâu nhị phân biểu diễn số nguyên t dưới dạng một số nguyên dương không dấu là chữ ký được tạo ra bởi hàm tạo chữ ký thay thế (xem Phụ lục A.6) Σ’ = t.

Vì kết quả trên lớn hơn n/2, nó được thay thế bởi phần dư của nó với n. Xâu nhị phân biểu diễn số nguyên này dưới dạng một số nguyên dương không dấu là chữ ký Σ = n – t.

Thông điệp đã ký có 128 xâu bộ tám chỉ bao gồm chữ ký vì M₂ là rỗng.

E.1.2.2.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. Số nguyên này tăng theo lũy thừa bậc 3 mô-đun n, do đó thu được số nguyên f_s.

Vì f_s là đồng dư với (n -12) mô-đun 16, nó được thay thế bởi phần dư của nó với n, có nghĩa là số nguyên được khôi phục là f’_r = n – f_s.

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r. Hàm tạo mặt nạ MGF1 áp dụng cho 848 (= 1024 – 160 – 16) bit bên trái nhất của S’_r, từ đó thu được xâu được khôi phục tạm thời S’_i.

S’_i biểu diễn xâu được khôi phục trung gian như sau.

– Bit bên trái nhất của S’_i được thiết lập bằng ‘0’ vì δ = 1 {δ = (1 – 1024)mod8). 37 xâu bộ tám bên trái nhất của xâu nhị phân còn lại bằng ‘0’; nó được theo sau bởi xâu bộ tám bao quanh “01”; 38 xâu bộ tám đó được chuyển sang bên trái của S’_i.

– Xâu bộ tám bên phải nhất của S’_i bằng “CC”; do đó, trailer bao gồm hai xâu bộ tám và bằng “33CC”; hai xâu bộ tám đó cũng được chuyển sang bên phải của S’_i.

Định danh hàm băm bằng “31”; do đó hàm băm được sử dụng là hàm băm chuyên dụng 1.

Xâu còn lại 704 bit được chia làm ba phần.

– M₁* bao gồm 384 bit bên trái nhất,

– S* bao gồm 160 bit bên phải nhất.

– H’ bao gồm 160 bit bên phải nhất.

Thông điệp đã được khôi phục M* chỉ bao gồm M₁* vì khôi phục thông điệp là toàn bộ. Mã băm còn lại H” được tính bằng các áp dụng hàm băm chuyên dụng 1 cho xâu nhị phân có độ dài 768 (=64+384+160+160), kết quả của việc ghép 64 bit của độ dài thông điệp đã được khôi phục C’, 384 bit của thông điệp đã được khôi phục M*, 160 bit của mã băm của phần thông điệp không thể khôi phục (phần này bằng rỗng) h(M₂) và 160 bit của salt đã được khôi phục S*. H” = h(C’||M₁*||h(M₂*)||S*).

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

E.1.2.3  Ví dụ về lược đồ chữ ký 3

Ví dụ này sử dụng hàm băm chuyên dụng 3 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là SHA-1).

E.1.2.3.1  Quá trình ký

Thông điệp để ký là rỗng, có nghĩa là một xâu nhị phân có độ dài bằng 0.

Vì lược đồ chữ ký này là thuộc kiểu tất định, giá trị salt S có độ dài bằng 0 được lựa chọn.

160 bit mã băm được tính toán bằng cách áp dụng hàm băm chuyên dụng 3 cho xâu nhị phân có độ dài 224 (= 64 + 160), kết quả của việc ghép thêm 64 bit độ dài thông điệp có thể khôi phục được C và 160 bit của mã băm của phần không thể khôi phục được (phần này bằng rỗng) h(M₂). H = h(C||h(M₂)).

Hàm băm được sử dụng đã được biết đến hoàn toàn. Do đó, trường trailer T bao gồm một xâu bộ tám duy nhất.

T = BC

Thông điệp là đủ ngắn để khôi phục toàn bộ. 1024 bit của xâu trung gian S_i kết quả của việc nối 855 (= 1024 – 160 – 8 – 1) bit đệm bằng ‘0’, bit bao quanh bằng 1, 160 bit của H và 8 bit của trường trailer T.

Xâu có thể khôi phục S_r thu được từ việc áp dụng hàm tạo mặt nạ MGF1 đối với 856 (= 1024 – 160 – 8) bit bên trái nhất của S_i, và 1 bit bên trái nhất của S_r được thiết lập bằng ‘0’ vì δ =1 (δ = 1 – 1024)mod 8).

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. f_r tăng theo lũy thừa bậc s theo mô-đun n. Kết quả được biểu diễn bởi một số nguyên dương không dấu tạm thời t.

Xâu nhị phân biểu diễn số nguyên t dưới dạng một số nguyên dương không dấu là chữ ký được tạo ra bởi hàm tạo chữ ký thay thế (xem Phụ lục A.6) Σ’ = t.

Vì kết quả trên lớn hơn n/2, chữ ký Σ = n – t.

Thông điệp đã ký có 128 xâu bộ tám chỉ bao gồm chữ ký vì M₂ là rỗng.

E.1.2.3.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. Số nguyên này tăng theo lũy thừa bậc 3 mô-đun n, do đó thu được số nguyên f_s.

Vì f_s là đồng dư với (n – 12) mô-đun 16, số nguyên được khôi phục là f’_r = n – f_s.

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r. Hàm tạo mặt nạ MGF1 áp dụng cho 856 (= 1024 – 160 – 8) bit bên trái nhất của S’_r, từ đó thu được xâu được khôi phục trung gian S’_i.

S’_i biểu diễn xâu được khôi phục trung gian như sau.

– Bit bên trái nhất của S’_i được thiết lập bằng ‘0’ vì δ – 1 (δ = (1 – 1024)mod8). 106 xâu bộ tám bên trái nhất của xâu nhị phân còn lại bằng ‘0’; nó được theo sau bởi xâu bộ tám bao quanh “01”; 107 xâu bộ tám đó được chuyển sang bên trái của S’_i.

– Xâu bộ tám bên phải nhất của S’_i bằng “BC”; xâu bộ tám đó cũng được chuyển sang bên phải của S’_i.

Vì trailer bằng “BC”, hàm băm được sử dụng đã được biết đến hoàn toàn; hàm băm chuyên dụng 3 trong ví dụ này.

Xâu còn lại 160 bit được giả định là mã băm H’ vì không còn thừa dữ liệu.

Thông điệp đã được khôi phục M’ được giả định là rỗng và do đó, khôi phục là toàn bộ. Mã băm khác H” được tính bằng cách áp dụng SHA-1 cho xâu nhị phân có độ dài 224 (=64+160), kết quả của việc ghép thêm 64 bit của độ dài thông điệp đã được khôi phục C’ và 160 bit của mã băm của phần thông điệp không thể khôi phục được (phần này bằng rỗng) h(M₂). H” = h(C’||h(M₂)).

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

E.1.3  Các ví dụ về khôi phục một phần

Ở đây trình bày ba ví dụ về tạo và xác thực chữ ký, mỗi ví dụ tương ứng với một trong ba lược đồ.

E.1.3.1  Ví dụ về lược đồ chữ ký 1

Ví dụ này sử dụng hàm băm chuyên dụng 1 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là RIPEMD-160).

E.1.3.1.1  Quá trình ký

Ví dụ này mô tả chữ ký của một thông điệp 132 xâu bộ tám, có nghĩa là 1056 bit.

160 bit mã băm được tính toán bằng cách áp dụng hàm băm chuyên dụng 1 cho 1056 bit của M.

Hàm băm được sử dụng đã được biết đến hoàn toàn. Do đó, trường trailer Tbao gồm 8 bit sau đây.

T = BC

Thông điệp là quá dài để có thể được khôi phục hoàn toàn bởi quá trình xác thực. Do đó, nó được chia làm hai phần.

– M₁ bao gồm 848 bit bên trái nhất.

– M₂ bao gồm 208 bit còn lại, có nghĩa là 26 xâu bộ tám.

1024 bit của xâu trung gian S_i kết quả của việc ghép thêm hai bit tiêu đề bằng “01″, bit dữ liệu thêm bằng ‘1’ bốn (= 1024 – 848 – 160 – 8 – 4) bit đệm bằng ‘0’, bit bao quanh bằng 1, 848 bit của M₁, 160 bit của H và 8 bit của trường trailer T. Xâu có thể khôi phục S_r kết quả của việc xâu bộ bốn bao quanh bằng 1 được thay thế bằng ‘A’.

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. f_r tăng theo lũy thừa bậc s theo mô-đun n. Kết quả được biểu diễn bởi một số nguyên dương không dấu tạm thời t.

Vì kết quả trên lớn hơn n/2, chữ ký Σ = n – t.

Thông điệp đã ký có 128 xâu bộ tám chữ ký Σ cùng với 26 xâu bộ tám của thông điệp không thể khôi phục được M₂, có nghĩa là chỉ nhiều hơn 22 xâu bộ tám so với thông điệp M.

E.1.3.1.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. Số nguyên này tăng theo lũy thừa bậc 3 mô-đun n, do đó thu được số nguyên f_s.

Vì f_s là đồng dư với (n – 12) mô-đun 16, nó được thay thế bởi phần dư của nó với n, có nghĩa là số nguyên được khôi phục là f’_r = n – f_s.

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r.

– Xâu bộ tám bên trái nhất của S’_r bằng “6A”; nó bao gồm tiêu đề bằng “01”, bit dữ liệu thêm bằng T (khôi phục một phần), một bit đệm bằng ‘0’ và một xâu bộ bốn đệm bằng ‘A’; xâu bộ tám này được chuyển sang bên trái của S’_r.

– Xâu bộ tám bên phải nhất của S’_r bằng “BC”; xâu bộ tám đó cũng được chuyển sang bên phải của S’_r.

Vì trailer bằng “BC”; hàm băm được sử dụng đã được biết đến hoàn toàn, hàm băm chuyên dụng 1 trong ví dụ này.

Xâu còn lại 1008 bit được chia làm hai phần.

– M₁* bao gồm 848 bit bên trái nhất.

– H’ bao gồm 160 bit bên phải nhất.

Vì khôi phục là một phần, thông điệp đã được khôi phục M* bao gồm M₁* và M₂*, phần có thể và không thể khôi phục được.

Mã băm còn lại H” được tính bằng các áp dụng hàm băm chuyên dụng 1 cho M*.

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

E.1.3.2  Ví dụ về lược đồ chữ ký 2

Ví dụ này sử dụng hàm băm chuyên dụng 3 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là SHA-1).

E.1.3.2.1  Quá trình ký

Thông điệp để ký là xâu 112 ký tự mã ASCII sau đây.

Trong hệ thập lục phân, thông điệp M là xâu bộ tám có độ dài 112 xâu bộ tám, có nghĩa là 896 bit sau đây.

160 bit của salt S được tạo ra.

Thông điệp là quá dài để có thể được khôi phục hoàn toàn bởi quá trình xác thực. Do đó, nó được chia làm hai phần.

– M₁ bao gồm 688 bit bên trái nhất.

– M₂ bao gồm 208 bit còn lại, có nghĩa là 26 xâu bộ tám.

160 bit của mã băm được tính bằng cách áp dụng hàm băm chuyên dụng 3 với xâu nhị phân có độ dài 1072 (= 64 + 688 + 160 + 160), kết quả của việc ghép 64 bit của độ dài phần không thể khôi phục được C, 688 bit của phần thông điệp có thể khôi phục được M₁, 160 bit của mã băm của phần không thể khôi phục được h(M₂) và 160 bit của salt S. H = h(C||M₁||h(M₂)||S).

Hàm băm được sử dụng đã được biết đến hoàn toàn. Do đó, trường trailer T bao gồm 8 bit sau đây.

1024 bit của xâu trung gian S_i kết quả của việc ghép thêm bảy (= 1024 – 688 – 160 – 160 – 8 – 1) bit đệm bằng ‘0’, bit bao quanh bằng 1, 688 bit của M₁, 160 bit của L, 160 bit của H và 8 bit của trường trailer T.

Xâu có thể khôi phục S_r thu được từ việc áp dụng hàm tạo mặt nạ MGF1 đối với 856 (= 1024 – 160 – 8) bit bên trái nhất của S_r, và 1 bit bên trái nhất của S_r được thiết lập bằng ‘0’ vì δ = 1 (δ = 1 – 1024)mod 8).

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. f_r tăng theo lũy thừa bậc s theo mô-đun n. Kết quả được biểu diễn bởi một số nguyên dương không dấu tạm thời t.

Xâu nhị phân biểu diễn số nguyên t dưới dạng một số nguyên dương không dấu là chữ ký được tạo ra bởi hàm tạo chữ ký thay thế (xem phụ lục B.6) Σ’ = t.

Vì kết quả trên lớn hơn n/2, chữ ký Σ = n – t.

Thông điệp đã ký có 128 xâu bộ tám chữ ký Σ cùng với 26 xâu bộ tám của thông điệp không thể khôi phục được M₂, có nghĩa là chỉ nhiều hơn 42 xâu bộ tám so với thông điệp M.

E.1.3.2.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. số nguyên này tăng theo lũy thừa bậc 3 mô-đun n, do đó thu được số nguyên f_s.

Vì f_s là đồng dư với (n – 12) mô-đun 16, nó được thay thế bởi phần dư của nó với n, có nghĩa là số nguyên được khôi phục là f’_r = n – f_s.

f’_s được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r. Hàm tạo mặt nạ MGF1 đối với 856 (= 1024 – 160 – 8) bit bên trái nhất của S’_r , và thu được xâu đã được khôi phục trung gian S’_i.

S’_i biểu diễn xâu trung gian đã được khôi phục như sau.

– Bit bên trái nhất của S’_i được thiết lập bằng ‘0’ vì δ =1 (δ = 1 – 1024)mod 8). 7 bit bên trái nhất của xâu còn lại bằng ‘0’; nó được theo sau bởi bit bao quanh ‘1’; xâu bộ tám này được chuyển sang bên trái của S’_i.

– Xâu bộ tám bên phải nhất của S’_i bằng “BC”; xâu bộ tám đó cũng được chuyển sang bên phải của S’_i.

Vì trường trailer T bằng “BC”; hàm băm được sử dụng đã được biết đến hoàn toàn, hàm băm chuyên dụng 3 trong ví dụ này.

Xâu còn lại 1008 bit được chia làm ba phần.

– M₁* bao gồm 688 bit bên trái nhất,

– S* bao gồm 160 bit bên phải nhất.

– H’ bao gồm 160 bit bên phải nhất.

Vì khôi phục là một phần, thông điệp đã được khôi phục M* bao gồm M₁* và M₂*, phần có thể và không thể khôi phục được.

Mã băm còn lại H” được tính bằng các áp dụng hàm băm SHA-1 cho xâu nhị phân có độ dài 1072 (= 64 + 688 + 160 + 160), kết quả của việc ghép thêm 64 bit độ dài phần có thể khôi phục được C’, 688 bit của phần thông điệp đã được khôi phục M₁*, 160 bit của mã băm của phần thông điệp không thể khôi phục h(M₂*) và 160 bit của salt đã được khôi phục S*. H” = h(C’||M₁*||h(M₂*)||S*)

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

E.1.3.3  Ví dụ về lược đồ chữ ký 3

Ví dụ này sử dụng hàm băm chuyên dụng 3 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là SHA-1).

E.1.3.3.1  Quá trình ký

Ví dụ này mô tả chữ ký của một thông điệp 132 xâu bộ tám, có nghĩa là 1056 bit sau đây.

Vì lược đồ chữ ký này là thuộc kiểu tất định, một giá trị salt S có độ dài bằng 0 được lựa chọn.

Thông điệp là quá dài để có thể được khôi phục hoàn toàn bởi quá trình xác thực. Do đó, nó được chia làm hai phần.

– M₁ bao gồm 840 bit bên trái nhất.

– M₂ bao gồm 216 bit còn lại, có nghĩa là 27 xâu bộ tám.

160 bit của mã băm H được tính bằng cách áp dụng hàm băm chuyên dụng 3 với xâu nhị phân có độ dài 1064 (= 64 + 840 + 160), kết quả của việc ghép 64 bit của độ dài phần không thể khôi phục được C, 840 bit của phần thông điệp có thể khôi phục được M₁, 160 bit của mã băm của phần không thể khôi phục được h(M₂). H = h(C||M₁||h(M₂)).

Định danh trong trường trailer T xác định hàm băm được sử dụng, là hàm băm chuyên dụng 3; ISO/IEC 10118-3 thiết lập định danh cho hàm băm giá trị “33”. Do đó, trường trailer T bao gồm 16 bit sau đây.

1024 bit của xâu trung gian S_i kết quả của việc ghép thêm bảy (= 1024 – 840 – 160 – 16 – 1) bit đệm bằng ‘0’, bit bao quanh bằng 1, 840 bit của phần có thể khôi phục được M₁, 160 bit của mã băm của phần thông điệp không thể khôi phục được h(M₂) và 16 bit của trường trailer T.

Xâu có thể khôi phục S_r thu được từ việc áp dụng hàm tạo mặt nạ MGF1 đối với 848 (= 1024 – 160 – 16) bit bên trái nhất của S_i, và 1 bit bên trái nhất của S_r được thiết lập bằng ‘0’ vi δ =1 (δ = 1- 1024)mod 8).

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. f_r tăng theo lũy thừa bậc s theo mô-đun n. Kết quả nhỏ hơn n/2 vẫn được giữ nguyên. Xâu nhị phân biểu diễn số nguyên đó dưới dạng một số nguyên dương không dấu là chữ ký Σ.

Trong ví dụ này, chữ ký được tạo ra bởi hàm tạo chữ ký thay thế (xem phụ lục B.6) cũng là một xâu nhị phân Σ, Σ’ = Σ.

Thông điệp đã ký có 128 xâu bộ tám chữ ký Σ cùng với 27 xâu bộ tám của thông điệp không thể khôi phục được M₂, có nghĩa là chỉ nhiều hơn 23 xâu bộ tám so với thông điệp M.

E.1.3.3.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. Số nguyên này tăng theo lũy thừa bậc 3 mô-đun n, do đó thu được số nguyên f_s.

Vì f_s là đồng dư với (n – 12) mô-đun 16, có nghĩa là số nguyên được khôi phục là f’_s = f_s.

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r. Hàm tạo mặt nạ MGF1 đối với 848 (= 1024 – 160 – 16) bit bên trái nhất của S’_r, và thu được xâu đã được khôi phục trung gian S’_i.

S’_i biểu diễn xâu trung gian đã được khôi phục như sau.

– Bit bên trái nhất của S’_i được thiết lập bằng ‘0’ vì δ =1 (δ = 1 – 1024)mod 8). 7 bit bên trái nhất của xâu còn lại bằng ‘0’; nó được theo sau bởi bit bao quanh T; xâu bộ tám này được chuyển sang bên trái của S’_i.

– Xâu bộ tám bên phải nhất của S’_i bằng “CC”; do đó, trường trailer bao gồm hai xâu bộ tám bằng “33CC”; hai xâu bộ tám đó cũng được chuyển sang bên phải của S’_i.

Định danh hàm băm bằng “33”; do đó, hàm băm được sử dụng là hàm băm chuyên dụng 3.

Xâu còn lại 1000 bit được chia làm hai phần.

– M₁* bao gồm 840 bit bên trái nhất.

– H‘ bao gồm 160 bit bên phải nhất.

Vì khôi phục là một phần, thông điệp đã được khôi phục M* bao gồm M₁* và M₂*, phần có thể và không thể khôi phục được.

Mã băm còn lại H” được tính bằng các áp dụng hàm băm SHA-1 cho xâu nhị phân có độ dài 1064 (= 64 + 840 + 160), kết quả của việc ghép thêm 64 bit độ dài phần có thể khôi phục được C’, 840 bit của phần thông điệp đã được khôi phục M₁* và 160 bit của mã băm của phần thông điệp không thể khôi phục h(M₂*). H” = h(C’||M₁*||h(M₂*))

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

E.2  Các ví dụ với số mũ công khai bằng 2

Phụ lục E.2 bao gồm các ví dụ với khóa công khai có số mũ bằng 2.

E.2.1  Ví dụ về quá trình tạo khóa

Khóa trong ví dụ có mô-đun k = 1024 bit với số mũ công khai v = 2. Vì số mũ xác thực công khai v là số chẵn, một thừa số nguyên tố bí mật là đồng dư với 3 theo mô-đun 8 và thừa số còn lại là đồng dư với 7 theo mod 8.

Số đồng dư công khai n là kết quả của các thừa số nguyên tố bí mật p và q. Độ dài của nó là 1024 bit.

Số mũ của chữ ký bí mật s bằng nghịch đảo phép nhân của v mod lcm(p – 1, q – 1)/2.

E.2.2  Các ví dụ về khôi phục toàn bộ

Ở đây trình bày ba ví dụ về tạo và xác thực chữ ký, mỗi ví dụ tương ứng với một trong ba lược đồ.

E.2.2.1  Ví dụ về lược đồ chữ ký 1

Ví dụ này sử dụng hàm băm chuyên dụng 3 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là SHA-1).

E.2.2.1.1  Quá trình ký

Trong hệ thập lục phân, thông điệp M là một xâu có độ dài là 48 xâu bộ tám, nghĩa là 384 bit như sau.

160 bit mã băm được tính toán bằng cách áp dụng hàm băm chuyên dụng 3 cho 384 bit của M.

Hàm băm được sử dụng đã được biết hoàn toàn. Do đó, trường trailer bao gồm 8 bit sau đây.

Thông điệp là đủ ngắn để khôi phục toàn bộ. 1024 bit của xâu trung gian S_i kết quả của việc nối hai bit của tiêu đề bằng “01”, bit dữ liệu thêm được thiết lập bằng ‘0’, 468 (= 1024 – 384 -.160 – 8 – 4) bit đệm bằng ‘0’, bit bao quanh bằng 1, 384 bit của M₁ (=M), 160 bit của H và 8 bit của trường trailer T. Xâu S_r có thể khôi phục kết quả của việc thay thế 116 xâu bộ bốn đệm bằng ‘0’ bằng 116 xâu bộ bốn đệm bằng ‘B’ và tương tự đối với xâu bộ bốn bao quanh bằng ‘1’ thay thế bằng ‘A’.

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. Vì ký hiệu Jacobi của f_r theo n bằng 1, kết quả được giữ lại. l_r tăng theo lũy thừa bậc s theo mô-đun n. Vì nhỏ hơn n/2 nên kết quả được giữ lại. Xâu nhị phân biểu diễn số nguyên đó dưới dạng số nguyên dương không dấu là chữ ký Σ.

Thông điệp đã ký có 128 xâu bộ tám chỉ bao gồm chữ ký vì M₂ là rỗng.

E.2.2.1.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. số nguyên này tăng theo lũy thừa bậc 2 mô-đun n, do đó thu được số nguyên f_s.

Quá trình xác thực không liên quan đến ký hiệu Jacobi. Vì ba bit trọng số nhỏ nhất của số nguyên kết quả fs bằng “001”, f’_r = n – f_s.

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r.

– Xâu bộ tám bên trái nhất của S’_r bằng “4B”; nó bao gồm tiêu đề bằng “01”, bit dữ liệu thêm bằng ‘0’ (khôi phục toàn bộ), một bit đệm bằng ‘0’ và một xâu bộ bốn đệm bằng ‘B’; theo sau là 115 xâu bộ bốn bằng ‘B’ và xâu bộ bốn bao quanh bằng ‘A’; 59 xâu bộ tám này được chuyển sang bên trái của S’_r.

– Xâu bộ tám bên phải nhất của S’_r bằng “BC”; xâu bộ tám đó cũng được chuyển sang bên phải của S’_r.

Vì trường trailer T bằng “BC”, hàm băm được sử dụng đã được biết đến hoàn toàn: hàm băm chuyên dụng 3 trong ví dụ này.

Xâu còn lại 544 bit được chia làm hai phần.

– M₁* bao gồm 384 bit bên trái nhất.

– H‘ bao gồm 160 bit bên phải nhất.

Thông điệp đã được khôi phục M* chỉ bao gồm M₁* vì khôi phục thông điệp là toàn bộ. Mã băm còn lại H” được tính bằng các áp dụng SHA-1 cho M*.

Vì hai mã băm H’ và H” là giống nhau, chữ ký 1 được chấp nhận.

E.2.2.2  Ví dụ về lược đồ chữ ký 2

Ví dụ này sử dụng hàm băm chuyên dụng 1 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là RIPEMD 160).

E.2.2.2.1  Quá trình ký

Thông điệp để ký là rỗng, có nghĩa là một xâu nhị phân có độ dài bằng 0.

160 bit của salt S được tạo ra.

160 bit mã băm được tính toán bằng cách áp dụng hàm băm chuyên dụng 1 để thu được một xâu nhị phân có độ dài là 384 (= 64 + 160 + 160) và kết quả được ghép thêm 64 bit độ dài thông điệp có thể khôi phục được C, 160 bit của mã băm của phần không thể khôi phục được h(M₂) và 160 bit của salt S. H = h(C||h(M₂)||S)

Hàm băm được sử dụng đã được biết đến hoàn toàn. Do đó, trường trailer T bao gồm 8 bit sau đây.

Thông điệp là rỗng, do đó là khôi phục toàn bộ. 1024 bit của xâu trung gian S_i kết quả của việc nối 695 (= 1024 – 160 – 160 – 8 – 1) bit đệm bằng ‘0’, bit bao quanh bằng 1, 160 bit của S, 160 bit của H và 8 bit của trường trailer T.

Xâu có thể khôi phục S_r thu được từ việc áp dụng hàm tạo mặt nạ MGF1 đối với 856 (= 1024 – 160 – 8) bit bên trái nhất của S_i, và 1 bit bên trái nhất của S_r được thiết lập bằng ‘0’ vì δ =1 (δ = 1 – 1024)mod 8).

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. Vì ký hiệu Jacobi của f_r theo n bằng -1, số nguyên đại diện là J = f_r /2.

J tăng theo lũy thừa bậc s mô-đun n. Kết quả như sau.

Vì kết quả trên lớn hơn n/2, chữ ký Σ = n – t.

Thông điệp đã ký có 128 xâu bộ tám chỉ bao gồm chữ ký vì M₂ là rỗng.

E.2.2.2.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. Số nguyên này tăng theo lũy thừa bậc 2 mô-đun n, do đó thu được số nguyên f_s.

Quá trình xác thực không liên quan đến ký hiệu Jacobi. Vì ba bit trọng số nhỏ nhất của số nguyên kết quả f_s bằng “100”, f’_r = 2f_s.

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r. Hàm tạo mặt nạ MGF1 áp dụng cho 856 (= 1024 – 160 – 8) bit bên trái nhất của S’_r, từ đó thu được xâu được khôi phục tạm thời S’_i.

S’_i biểu diễn xâu được khôi phục trung gian như sau.

– Bit bên trái nhất của S’_i được thiết lập bằng ‘0’ vì δ = 1 (δ = (1 – 1024)mod8). 695 bit bên trái nhất của xâu nhị phân còn lại bằng ‘0’; nó được theo sau bởi bit bao quanh “1”; 87 xâu bộ tám đó được chuyển sang bên trái của S’_i.

– Xâu bộ tám bên phải nhất của S’_i bằng “BC”; xâu bộ tám đó cũng được chuyển sang bên phải của S’_i.

Vì trailer bằng “BC”, hàm băm được sử dụng đã được biết đến hoàn toàn: hàm băm chuyên dụng 1 trong ví dụ này.

Xâu còn lại 320 bit được chia làm hai phần.

– S* bao gồm 160 bit bên phải nhất.

– H’ bao gồm 160 bit bên phải nhất.

Thông điệp đã được khôi phục M* được giả định là rỗng, và do đó khôi phục thông điệp là toàn bộ. Mã băm còn lại H” được tính bằng các áp dụng hàm băm chuyên dụng 1 cho xâu nhị phân có độ dài 384 (=64+160+160), kết quả của việc ghép 64 bit của độ dài thông điệp đã được khôi phục C’, 160 bit của mã băm của phần thông điệp không thể khôi phục h(M₂) và 160 bit của salt đã được khôi phục S*. H” = h(C‘||h(M₂)||S*).

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

E.2.2.3  Ví dụ về lược đồ chữ ký 3

Ví dụ này sử dụng hàm băm chuyên dụng 3 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là SHA-1).

E,1.2.3.1  Quá trình ký

Thông điệp để ký là xâu 64 ký tự mã ASCII sau đây.

Trong hệ thập lục phân, thông điệp M là xâu có độ dài là 64 xâu bộ tám, có nghĩa là 512 bit sau đây.

Vì lược đồ chữ ký này là thuộc kiểu tất định, giá trị salt S có độ dài bằng 0 được lựa chọn.

160 bit mã băm được tính toán bằng cách áp dụng hàm băm chuyên dụng 3 cho xâu nhị phân có độ dài 736 (= 64 + 512 + 160), kết quả của việc ghép thêm 64 bit độ dài thông điệp có thể khôi phục được C, 512 bit của phần thông điệp có thể khôi phục được M₁ và 160 bit của mã băm của phần không thể khôi phục được h(M₂). H = h(C||M₁||h(M₂)).

Định danh trong trường trailer xác định hàm băm được sử dụng, ISO/IEC thiết lập định danh cho hàm băm chuyên dụng 3 giá trị “33”. Do đó, trường trailer T bao gồm 16 bit sau đây.

Thông điệp là đủ ngắn để khôi phục toàn bộ. 1024 bit của xâu trung gian S_i kết quả của việc nối 335 (= 1024 – 512 – 160 – 16 – 1) bit đệm bằng ‘0’, bit bao quanh bằng 1, 512 bit của M₁(=M), 160 bit của S, 160 bit của H và 16 bit của trường trailer T.

Xâu có thể khôi phục S_r thu được từ việc áp dụng hàm tạo mặt nạ MGF1 đối với 848 (= 1024 – 160 – 16) bit bên trái nhất của S_i, và 1 bit bên trái nhất của S_r được thiết lập bằng ‘0’ vì δ =1 (δ = 1 – 1024)mod 8).

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. Vì ký hiệu Jacobi của f_r theo n bằng -1, số nguyên đại diện là J = f_r/2.

J tăng theo lũy thừa bậc s mô-đun n. Vì kết quả nhỏ hơn n/2, chữ ký Σ = J^s.

Thông điệp đã ký có 128 xâu bộ tám chỉ bao gồm chữ ký vì M₂ là rỗng.

E.2.2.3.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. Số nguyên này tăng theo lũy thừa bậc 2 mô-đun n, do đó thu được số nguyên f_s.

Quá trình xác thực không liên quan đến ký hiệu Jacobi. Vì ba bit trọng số nhỏ nhất của số nguyên kết quả f_s bằng “110”, f’_r = 2f_s.

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r. Hàm tạo mặt nạ MGF1 áp dụng cho 848 (= 1024 – 160 – 16) bit bên trái nhất của S’_r, từ đó thu được xâu được khôi phục trung gian S’_i.

S’_i biểu diễn xâu được khôi phục trung gian như sau.

– Bit bên trái nhất của S’_i được thiết lập bằng ‘0’ vì δ = 1 (δ = (1 – 1024)mod8). 335 xâu bộ tám bên trái nhất của xâu nhị phân còn lại bằng ‘0’; nó được theo sau bởi bit bao quanh T; 42 xâu bộ tám đó được chuyển sang bên trái của S’_i.

– Xâu bộ tám bên phải nhất của S’_i bằng “CC”; do đó, trailer bao gồm hai xâu bộ tám bằng “33CC”; hai xâu bộ tám đó cũng được chuyển sang bên phải của S’_i.

Định danh hàm băm bằng “33”; do đó hàm băm được sử dụng là hàm băm chuyên dụng 3.

Xâu còn lại 672 bit được chia làm hai phần.

– M₁* bao gồm 512 bit bên trái nhất.

– H’ bao gồm 160 bit bên phải nhất.

Thông điệp đã được khôi phục M* chỉ bao gồm M₁* và do đó, khôi phục là toàn bộ. Mã băm khác H” được tính bằng cách áp dụng SHA-1 cho xâu nhị phân có độ dài 736 (= 64 + 512 + 160), kết quả của việc ghép thêm 64 bit của độ dài thông điệp đã được khôi phục C’, 512 bit của phần thông điệp đã được khôi phục M₁* và 160 bit của mã băm của phần thông điệp không thể khôi phục được (rỗng) h(M₂). H” = h(C’||M₁^*||h(M₂^*))

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

E.2.3  Các ví dụ về khôi phục một phần

Ở đây trình bày ba ví dụ về tạo và xác thực chữ ký, mỗi ví dụ tương ứng với một trong ba lược đồ.

E.2.3.1  Ví dụ về lược đồ chữ ký 1

Ví dụ này sử dụng hàm băm chuyên dụng 3 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là SHA-1).

E.2.3.1.1  Quá trình ký

Thông điệp để ký là xâu 112 ký tự mã ASCII sau đây.

Trong hệ thập lục phân, thông điệp M là xâu có độ dài 112 xâu bộ tám, có nghĩa là 896 bit sau đây.

160 bit mã băm được tính toán bằng cách áp dụng SHA-1 cho 896 bit của M.

Định danh trong trường trailer xác định hàm băm được sử dụng; ISO/IEC thiết lập định danh cho hàm băm chuyên dụng 3 giá trị “33”. Do đó, trường trailer T bao gồm 16 bit sau đây.

Thông điệp là quá dài để có thể được khôi phục hoàn toàn bởi quá trình xác thực. Do đó, nó được chia làm hai phần.

– M₁ bao gồm 840 bit bên trái nhất.

– M₂ bao gồm 56 bit còn lại, có nghĩa là 7 xâu bộ tám.

1024 bit của xâu trung gian Si kết quả của việc ghép thêm hai bit tiêu đề bằng “01”, bit dữ liệu thêm bằng ‘1’, bốn (= 1024 – 840 – 160 – 16 – 4) bit đệm bằng ‘0’, bit bao quanh bằng 1, 840 bit của M₁, 160 bit của H và 16 bit của trường trailer T. Xâu có thể khôi phục S_r kết quả của việc xâu bộ bốn bao quanh bằng 1 được thay thế bằng ‘A’.

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. Vì ký hiệu Jacobi của f_r theo n bằng -1, số nguyên đại diện là J = f_r/2.

J tăng theo lũy thừa bậc s mô-đun n. Kết quả như sau.

Vì kết quả trên lớn hơn n/2, chữ ký Σ = n – J^s.

Thông điệp đã ký có 128 xâu bộ tám chữ ký Σ cùng với 7 xâu bộ tám của thông điệp không thể khôi phục được M₂, có nghĩa là chỉ nhiều hơn 23 xâu bộ tám so với thông điệp M.

E.2.3.1.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. Số nguyên này tăng theo lũy thừa bậc 2 mô-đun n, do đó thu được số nguyên f_s.

Quá trình xác thực không liên quan đến ký hiệu Jacobi. Vì ba bit trọng số nhỏ nhất của số nguyên kết quả f_s bằng ”110”, f’_r = 2f_s.

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r.

– Xâu bộ tám bên trái nhất của S’_r bằng “6A”; nó bao gồm tiêu đề bằng “01”, bit dữ liệu thêm bằng ‘1’ (khôi phục một phần), một bit đệm bằng ‘0’ và một xâu bộ bốn đệm bằng ‘A’; xâu bộ tám này được chuyển sang bên trái của S’_r.

– Xâu bộ tám bên phải nhất của S’_r bằng “CC”; do đó trailer bao gồm hai xâu bộ tám bằng “33CC”; hai xâu bộ tám đó cũng được chuyển sang bên phải của S’_r.

Định danh hàm băm là “33”; do đó, hàm băm được sử dụng là hàm băm chuyên dụng 3.

Xâu còn lại 1000 bit được chia làm hai phần.

– M₁* bao gồm 840 bit bên trái nhất.

– H’ bao gồm 160 bit bên phải nhất.

Vì khôi phục là một phần, thông điệp đã được khôi phục M* bao gồm M₁* và M₂*, phần có thể và không thể khôi phục được.

Mã băm còn lại H” được tính bằng các áp dụng hàm băm chuyên dụng 3 cho M*.

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

E.2.3.2  Ví dụ về lược đồ chữ ký 2

Ví dụ này sử dụng hàm băm chuyên dụng 1 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là RIPEMD-160).

E.2.3.2.1  Quá trình ký

Ví dụ này mô tả chữ ký của một thông điệp có độ dài 132 xâu bộ tám, có nghĩa là 1056 bit sau đây.

160 bit của salt S được tạo ra.

Thông điệp là quá dài để có thể được khôi phục hoàn toàn bởi quá trình xác thực. Do đó, nó được chia làm hai phần.

– M₁ bao gồm 680 bit bên trái nhất.

– M₂ bao gồm 376 bit còn lại, có nghĩa là 47 xâu bộ tám.

160 bit của mã băm được tính bằng cách áp dụng hàm băm chuyên dụng 1 với xâu nhị phân có độ dài 1064 (= 64 + 680 + 160 + 160), kết quả của việc ghép 64 bit của độ dài phần không thể khôi phục được C, 680 bit của phần thông điệp có thể khôi phục được M₁, 160 bit của mã băm của phần không thể khôi phục được h(M₂) và 160 bit của salt S. H = h(C||M₁||h(M₂)||S).

Định danh trong trailer xác định hàm băm được sử dụng; ISO/IEC thiết lập định danh cho hàm băm chuyên dụng 1 giá trị “31”. Do đó, trường trailer T bao gồm 16 bit sau đây.

1024 bit của xâu trung gian S_i kết quả của việc ghép thêm bảy (= 1024 – 680 – 160 – 160 – 16 – 1) bit đệm bằng ‘0’, bit bao quanh bằng 1, 680 bit của M₁, 160 bit của L, 160 bit của H và 16 bit của trường trailer T.

Xâu có thể khôi phục S_r thu được từ việc áp dụng hàm tạo mặt nạ MGF1 đối với 848 (= 1024 – 160 – 16) bit bên trái nhất của S_i, và 1 bit bên trái nhất của S_r được thiết lập bằng ‘0’ vì δ =1 (δ = 1 – 1024)mod 8).

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. Vì ký hiệu Jacobi của f_r theo n bằng -1, số nguyên đại diện là J = f_r/2.

J tăng theo lũy thừa bậc s mô-đun n. Kết quả như sau.

Vì kết quả trên lớn hơn n/2, chữ ký Σ = n – f^s.

Thông điệp đã ký có 128 xâu bộ tám chữ ký Σ cùng với 47 xâu bộ tám của thông điệp không thể khôi phục được M₂, có nghĩa là chỉ nhiều hơn 43 xâu bộ tám so với thông điệp M.

E.2.3.2.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. Số nguyên này tăng theo lũy thừa bậc 2 mô-đun n, do đó thu được số nguyên f_s.

Quá trình xác thực không liên quan đến ký hiệu Jacobi. Vì ba bit trọng số nhỏ nhất của số nguyên kết quả f_s bằng “111”, f’_r – 2(n – f_s).

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r. Hàm tạo mặt nạ MGF1 đối với 848 (= 1024 – 160 – 16) bit bên trái nhất của S’_r, và thu được xâu đã được khôi phục trung gian S’_i.

S’_i biểu diễn xâu trung gian đã được khôi phục như sau.

– Bit bên trái nhất của S’_i được thiết lập bằng ‘0’ vì δ =1 (δ = 1 – 1024)mod 8). 7 bit bên trái nhất của xâu còn lại bằng ‘0’; nó được theo sau bởi bit bao quanh ‘1’; xâu bộ tám này được chuyển sang bên trái của S’_i.

– Xâu bộ tám bên phải nhất của S’_i bằng “CC”; do đó trailer bao gồm hai xâu bộ tám bằng “31CC”; hai xâu bộ tám đó cũng được chuyển sang bên phải của S’_i.

Định danh hàm băm bằng “31”; do đó hàm băm được sử dụng là hàm băm chuyên dụng 1.

Xâu còn lại 1000 bit được chia làm ba phần.

– M₁* bao gồm 680 bit bên trái nhất,

– S* bao gồm 160 bit bên phải nhất.

– H’ bao gồm 160 bit bên phải nhất.

Vì khôi phục là một phần, thông điệp đã được khôi phục M* bao gồm M₁* và M₂* phần có thể và không thể khôi phục được.

Mã băm còn lại H” được tính bằng các áp dụng hàm băm chuyên dụng 1 cho xâu nhị phân có độ dài 1064 (= 64 + 680 + 160 + 160), kết quả của việc ghép thêm 64 bit độ dài phần có thể khôi phục được C‘, 680 bit của phần thông điệp đã được khôi phục M₁*, 160 bit của mã băm của phần thông điệp không thể khôi phục h(M₁*) và 160 bit của salt đã được khôi phục S*. H” = h(C’||M₁^*||h(M₂^*)||S*).

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

E.2.3.3  Ví dụ về lược đồ chữ ký 3

Ví dụ này sử dụng hàm băm chuyên dụng 1 trong ISO/IEC 10118-3 (còn được biết đến với tên gọi là RIPEMD-160).

E.2.3.3.1  Quá trình ký

Thông điệp để ký là xâu 112 ký tự mã ASCII sau đây.

Trong hệ thập lục phân, thông điệp M là xâu có độ dài 112 xâu bộ tám, có nghĩa là 896 bit sau đây.

Vì lược đồ chữ ký này là thuộc kiểu tất định, một giá trị salt S có độ dài bằng 0 được lựa chọn.

Thông điệp là quá dài để có thể được khôi phục hoàn toàn bởi quá trình xác thực. Do đó, nó được chia làm hai phần.

– M₁ bao gồm 848 bit bên trái nhất.

– M₂ bao gồm 48 bit còn lại, có nghĩa là 6 xâu bộ tám.

160 bit của mã băm H được tính bằng cách áp dụng hàm băm chuyên dụng 1 với xâu nhị phân có độ dài 1072 (= 64 + 848 + 160), kết quả của việc ghép 64 bit của độ dài phần không thể khôi phục được C, 848 bit của phần thông điệp có thể khôi phục được M₁, 160 bit của mã băm của phần không thể khôi phục được h(M₂). H = h(C||M₁||h(M₂)).

Hàm băm được sử dụng đã được biết đến hoàn toàn. Do đó, trường trailer 7 bao gồm 8 bit sau đây.

1024 bit của xâu trung gian S_i kết quả của việc ghép thêm bảy (= 1024 – 848 – 160 – 8 – 1) bit đệm bằng ‘0’, bit bao quanh bằng 1, 848 bit của phần có thể khôi phục được M₁, 160 bit của mã băm của phần thông điệp không thể khôi phục được h(M₂) và 8 bit của trường trailer T.

Xâu có thể khôi phục S_r thu được từ việc áp dụng hàm tạo mặt nạ MGF1 đối với 856 (= 1024 – 160 – 8) bit bên trái nhất của S_i, và 1 bit bên trái nhất của S_r được thiết lập bằng ‘0’ vì δ =1 (δ = 1 – 1024)mod 8).

Số nguyên có thể khôi phục f_r là số nguyên dương không dấu biểu diễn S_r. Vì ký hiệu Jacobi của f_r theo n bằng 1, kết quả được giữ nguyên. f_r tăng theo lũy thừa bậc s theo mô-đun n. Kết quả được biểu diễn bởi một số nguyên dương không dấu tạm thời t.

Vì kết quả trên lớn hơn n/2, nó được thay thế bởi phần dư của nó với n. Xâu nhị phân biểu diễn số nguyên này dưới dạng một số nguyên dương không dấu là chữ ký Σ = n – t.

Thông điệp đã ký có 128 xâu bộ tám chữ ký Σ cùng với 6 xâu bộ tám của thông điệp không thể khôi phục được M₂, có nghĩa là chỉ nhiều hơn 22 xâu bộ tám so với thông điệp M.

E.2.3.3.2  Quá trình xác thực

Chữ ký Σ là một xâu nhị phân đại diện một số nguyên dương không dấu, nhỏ hơn n/2. Số nguyên này tăng theo lũy thừa bậc 2 mô-đun n, do đó thu được số nguyên f_s.

Quá trình xác thực không liên quan đến ký hiệu Jacobi. Vì ba bit trọng số nhỏ nhất của số nguyên kết quả f_s bằng “100”, f’_r = f_s.

f’_r được biểu diễn dưới dạng một số nguyên dương không dấu bởi xâu đã được khôi phục S’_r. Hàm tạo mặt nạ MGF1 đối với 856 (= 1024 – 160 – 8) bit bên trái nhất của S’_r, và thu được xâu đã được khôi phục trung gian S’_i.

S’_i biểu diễn xâu trung gian đã được khôi phục như sau.

– Bit bên trái nhất của S’_i được thiết lập bằng ‘0’ vì δ = 1 (δ = 1 – 1024)mod 8). 7 bit bên trái nhất của xâu còn lại bằng ‘0’; nó được theo sau bởi bit bao quanh ‘1’; xâu bộ tám này được chuyển sang bên trái của S’_i.

– Xâu bộ tám bên phải nhất của S’_i bằng “BC”; xâu bộ tám đó cũng được chuyển sang bên phải của S’_i.

Vì trailer bằng “BC”, hàm băm được sử dụng đã được biết đến hoàn toàn: RIPEMD-160 trong ví dụ này.

Xâu còn lại 1008 bit được chia làm hai phần.

– M₁* bao gồm 848 bit bên trái nhất.

– H‘ bao gồm 160 bit bên phải nhất.

Vì khôi phục là một phần, thông điệp đã được khôi phục M* bao gồm M₁* và M₂*, phần có thể và không thể khôi phục được.

Mã băm còn lại H” được tính bằng các áp dụng hàm băm chuyên dụng 1 cho xâu nhị phân có độ dài 1072 (= 64 + 848 + 160), kết quả của việc ghép thêm 64 bit độ dài phần có thể khôi phục được C’, 848 bit của phần thông điệp đã được khôi phục M₁* và 160 bit của mã băm của phần thông điệp không thể khôi phục h(M₂*). H” = h(C’||M₁^*||h(M₂^*)).

Vì hai mã băm H’ và H” là giống nhau, chữ ký Σ được chấp nhận.

 

Thư mục tài liệu tham khảo

[1] M. Bellare and P. Rogaway, Random oracles are practical: a paradigm for designing efficient protocol. In: Proceedings of the first annual conference on Computer and Communications Security, ACM, 1993, pp.62-73.

[2] M. Bellare and P. Rogaway, Optimal asymmetric encryption – how to encrypt with RSA’. In: A. De Santis (editor), Advances in Cryptology – Eurocrypt ‘94, Lecture Notes in Computer Science 950 (1995), Springer-Verlag, pp.92-111.

[3] M. Bellare and P. Rogaway, The exact security of digital signatures: How to sign with RSA and Rabin. In: U.M. Maurer (editor), Advances in Cryptology – Eurocrypt ’96, Lecture Notes in Computer Science 1070 (1996), Springer-Verlag, pp.399-416.

[4] J.-S. Coron, On the exact security of full domain hashing. In: M. Bellare (editor), Advances in Cryptology – Crypto 2000, Lecture Notes in Computer Science 1880 (2000), Springer-Verlag, pp.229-235.

[5] J.-S. Coron, D. Naccache, and J.P. stern, On the security of RSA padding. In: M.J. Wiener (editor), Advances in Cryptology – Crypto ’99, Lecture Notes in Computer Science 1666, (1999) , Springer-Verlag, pp.1-18.

[6] J.-S. Coron, D. Naccache, M. Tibouchi, and R.-P. Weinmann. Practical Cryptanalysis of ISO 9796-2 and Europay-Mastercard-Visa Signatures. In: S. Halevi (editor), Advances in Cryptology – Crypto 2009, Lecture Notes in Computer Science 5677 (2009), Springer-Verlag, pp.428-444.

[7] M. Girault and J.-F. Misarsky, Cryptanalysis of countermeasures proposed for repairing ISO 9796-1. In: B. Preneel (editor), Advances in Cryptology – Eurocrypt 2000, Lecture Notes in Computer Science 1807 (2000), Springer-Verlag, pp.81-90.

[8] F. Grieu, A chosen messages attack on the ISO/IEC 9796-1 signature scheme. In: B. Preneel (editor), Advances in Cryptology – Eurocrypt 2000, Lecture Notes in Computer Science 1807 (2000) , Springer-Verlag, pp.70-80.

[9] IEEE Std 1363-2000, Standard specifications for public key cryptography.

[10] IEEE Std 1363a-2004, Standard specifications for public key cryptography – Amendment 1: Additional techniques.

[11] ISO/IEC 9796-3:2006, Information technology – Security techniques – Digital signature schemes giving message recovery – Part 3: Discrete logarithm based mechanisms.

[12] ISO/IEC 9797-2:2002, Information technology – Security techniques – Message Authentication Codes (MACS) – Part 2: Mechanisms using a dedicated hash-function.

[13] TCVN 11817-1:19971), Information technology – Security techniques – Entity authentication – Part 1: General.

[14] TCVN 12214 (all parts), Information technology – Security techniques – Digital signatures with appendix.

[15] J. Jonsson, Security proofs for the RSA-PSS signature scheme and its variants. Proceedings of the 2nd NESS/E Workshop, Royal Holloway, University of London, September 2001. Full version available in IACR cryptology archive 2001/053.

[16] B. Kaliski, On hash function firewalls in signature schemes. In: B. Preneel (editor), Cryptographers’ Track RSA Conference 2002, Lecture Notes in Computer Science 2271 (2002), Springer-Verlag, pp.1-16.

 

Mục Lục

Lời nói đầu

1  Phạm vi áp dụng

2  Tài liệu viện dẫn

3  Thuật ngữ và định nghĩa

4  Ký hiệu và chữ viết tắt

5  Sự chuyển đổi giữa các xâu bit và số nguyên

6  Yêu cầu

7  Mô hình quá trình ký và xác thực

7.1  Tổng quan

7.2  Ký thông điệp

7.3  Xác thực chữ ký

7.4  Quy định lược đồ chữ ký

8  Lược đồ chữ ký số 1

8.1  Tổng quan

8.2  Tham số

8.3  Tạo giá trị đại diện của thông điệp

8.4  Khôi phục thông điệp

9.  Lược đồ chữ ký số 2

9.1  Tổng quan

9.2  Tham số

9.3  Tạo giá trị đại diện của thông điệp

9.4  Khôi phục thông điệp

10  Lược đồ chữ ký số 3

Phụ lục A (quy định) Mô-đun ASN.1

Phụ lục B (quy định) Hệ thống khóa công khai cho chữ ký số

Phụ lục C (quy định) Hàm tạo mặt nạ

Phụ lục D (tham khảo) về định danh hàm băm và sự lựa chọn độ dài có thể khôi phục được của thông điệp

Phụ lục E (tham khảo) Ví dụ

Thư mục tài liệu tham khảo