Nội dung toàn văn Tiêu chuẩn quốc gia TCVN 142:2009 về Số ưu tiên và dãy số ưu tiên
TIÊU CHUẨN QUỐC GIA
TCVN 142 : 2009
SỐ ƯU TIÊN VÀ DÃY SỐ ƯU TIÊN
Preferred numbers and series of preferred numbers
Lời nói đầu
TCVN 142 : 2009 thay thế cho TCVN 142-88;
TCVN 142 : 2009 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 12 Đại lượng và đơn vị đo biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
SỐ ƯU TIÊN VÀ DÃY SỐ ƯU TIÊN
Preferred numbers and series of preferred numbers
1. Phạm vi áp dụng
Tiêu chuẩn quy định số ưu tiên và dãy số ưu tiên sử dụng khi xác định dãy thông số và giá trị riêng biệt của các thông số của sản phẩm dựa trên cơ sở các cấp số nhân.
Tiêu chuẩn này không áp dụng đối với những giá trị của các thông số quan hệ với những giá trị đã được công nhận của các thông số khác bằng sự phụ thuộc hàm số, cũng như đối với các trường hợp khi thay những giá trị của các thông số bằng những số ưu tiên sẽ làm giảm chất lượng sản phẩm hoặc gây thiệt hại cho nền kinh tế.
2. Quy định chung
2.1. Số ưu tiên là trị số quy tròn của các số hạng của cấp số nhân có chứa các lũy thừa nguyên của mười với công bội:
|
|
|
|
|
|
|
trong khoảng từ 1 đến 10. Vì dãy số ưu tiên không giới hạn cả hai phía, cho nên những số ưu tiên trong các khoảng thập phân khác được lập bằng cách nhân những trị số trong Bảng 2 và Bảng 4 với lũy thừa nguyên (dương hoặc âm) của mười, có nghĩa là những số ưu tiên lớn hơn 10 được lập bằng cách nhân với 10; 100, 1 000… những số nhỏ hơn 1 – nhân với 0,1; 0,01; 0,001; …
2.2. Dãy cơ bản và dãy phụ của số ưu tiên chứa tất cả lũy thừa nguyên của 10.
2.3. Tích hay thương của hai số ưu tiên bất kỳ của dãy cơ bản hoặc dãy phụ là số ưu tiên của dãy đó.
Lũy thừa nguyên dương hoặc lũy thừa nguyên âm của số ưu tiên bất kỳ của dãy cơ bản hoặc dãy phụ là số ưu tiên của dãy đó.
CHÚ THÍCH: Trong những trường hợp này có thể có sai số do sự khác nhau giữa những số ưu tiên thực và những số ưu tiên quy tròn tương ứng trong dãy cơ bản.
2.4. Khi xác định dãy các thông số cần chọn dãy số ưu tiên có công bội lớn nhất thỏa mãn những yêu cầu đã định trước.
2.5. Ưu tiên sử dụng những dãy số ưu tiên có cùng công bội hơn những dãy phối hợp có nhiều công bội.
2.6. Ví dụ về việc sử dụng số ưu tiên và dãy số ưu tiên cho ở Phụ lục A và Phụ lục B.
3. Dãy cơ bản
3.1. Dãy cơ bản của số ưu tiên có ký hiệu và công bội quy định trong Bảng 1 và có các số hạng trong khoảng từ 1 đến 10 trong Bảng 2.
3.2. Những ký hiệu dãy cơ bản ghi trong Bảng 1 tương ứng với những dãy không bị giới hạn ở cả hai phía. Trường hợp có giới hạn, trong ký hiệu ghi rõ giới hạn:
R10 (1,25…) – dãy R10 có giới hạn dưới là 1,25 (bao gồm cả 1,25).
R20 (… 45) – dãy R20 có giới hạn trên là 45 (bao gồm cả 45).
R40 (75.300) – dãy R40 có giới hạn dưới là 75 và giới hạn trên là 300 (bao gồm cả hai số hạng 75 và 300).
Bảng 1 – Ký hiệu và công bội quy định của dãy số ưu tiên cơ bản
|
Ký hiệu dãy cơ bản |
Công bội của dãy |
|
|
Trị số quy tròn |
Trị số thực |
|
|
R5 |
1,6 |
|
|
R10 |
1,25 |
|
|
R20 |
1,12 |
|
|
R40 |
1,06 |
|
Bảng 2 – Các số hạng của dãy số ưu tiên cơ bản
|
R5 |
R10 |
R20 |
R40 |
Số thứ tự của số ưu tiên N |
Phần định trị của lôgarit thập phân |
Trị số tính toán của số ưu tiên |
Sai lệch giữa số ưu tiên của dãy cơ bản và trị số tính toán, % |
|
1,0 |
1,00 |
1,00 |
1,00 |
0 |
000 |
1,000 0 |
0,00 |
|
|
|
|
1,06 |
1 |
025 |
1,059 3 |
+ 0,07 |
|
|
|
1,12 |
1,12 |
2 |
050 |
1,122 0 |
– 0,18 |
|
|
|
|
1,18 |
3 |
075 |
1,188 5 |
– 0,71 |
|
|
1,25 |
1,25 |
1,25 |
4 |
100 |
1,258 9 |
– 0,71 |
|
|
|
|
1,32 |
5 |
125 |
1,333 5 |
– 1,01 |
|
|
|
1,40 |
1,40 |
6 |
150 |
1,412 5 |
– 0,88 |
|
|
|
|
1,50 |
7 |
175 |
1,496 2 |
+ 0,25 |
|
1,6 |
1,60 |
1,60 |
1,60 |
8 |
200 |
1,584 9 |
+ 0,95 |
|
|
|
|
1,70 |
9 |
225 |
1,678 8 |
+ 1,26 |
|
|
|
1,80 |
1,80 |
10 |
250 |
1,778 3 |
+ 1,22 |
|
|
|
|
1,90 |
11 |
275 |
1,883 6 |
+ 0,87 |
|
|
2,00 |
2,00 |
2,00 |
12 |
300 |
1,995 3 |
+ 0,24 |
|
|
|
|
2,12 |
13 |
325 |
2,113 5 |
+ 0,31 |
|
|
|
2,24 |
2,24 |
14 |
350 |
2,238 7 |
+ 0,06 |
|
|
|
|
2,36 |
15 |
375 |
2,371 4 |
– 0,48 |
|
2,5 |
2,50 |
2,50 |
2,50 |
16 |
400 |
2,511 9 |
– 0,47 |
|
|
|
|
2,65 |
17 |
425 |
2,660 7 |
– 0,40 |
|
|
|
2,80 |
2,80 |
18 |
450 |
2,818 4 |
– 0,65 |
|
|
|
|
3,00 |
19 |
475 |
2,985 4 |
+ 0,49 |
|
|
3,15 |
3,15 |
3,15 |
20 |
500 |
3,162 3 |
– 0,39 |
|
|
|
|
3,35 |
21 |
525 |
3,349 7 |
+ 0,01 |
|
|
|
3,55 |
3,55 |
22 |
550 |
3,548 1 |
+ 0,05 |
|
|
|
|
3,75 |
23 |
575 |
3,758 4 |
– 0,22 |
|
4,0 |
4,00 |
4,00 |
4,00 |
24 |
600 |
3,981 1 |
+ 0,47 |
|
|
|
|
4,25 |
25 |
625 |
4,217 0 |
+ 0,78 |
|
|
|
4,50 |
4,50 |
26 |
650 |
4,466 8 |
+ 0,74 |
|
|
|
|
4,75 |
27 |
675 |
4,731 5 |
+ 0,39 |
|
|
5,00 |
5,00 |
5,00 |
28 |
700 |
5,011 9 |
– 0,24 |
|
|
|
|
5,30 |
29 |
725 |
5,308 8 |
– 0,17 |
|
|
|
5,60 |
5,60 |
30 |
750 |
5,623 4 |
– 0,42 |
|
|
|
|
6,00 |
31 |
775 |
5,956 6 |
+ 0,73 |
|
6,3 |
6,30 |
6,30 |
6,30 |
32 |
800 |
6,309 6 |
– 0,15 |
|
|
|
|
6,70 |
33 |
825 |
6,683 4 |
+ 0,25 |
|
|
|
7,10 |
7,10 |
34 |
850 |
7,079 5 |
+ 0,29 |
|
|
|
|
7,50 |
35 |
870 |
7,498 9 |
+ 0,01 |
|
|
8,00 |
8,00 |
8,00 |
36 |
900 |
7,943 3 |
+ 0,71 |
|
|
|
|
8,50 |
37 |
925 |
8,414 0 |
+ 1,02 |
|
|
|
9,00 |
9,00 |
38 |
950 |
8,912 5 |
+ 0,98 |
|
|
|
|
9,50 |
39 |
975 |
9,440 6 |
+ 0,63 |
|
10,0 |
10,00 |
10,00 |
10,00 |
40 |
1 000 |
10,000 0 |
0,00 |
4. Dãy phụ
Dãy phụ của số ưu tiên có ký hiệu và công bội quy định trong Bảng 3 và có các số hạng trong khoảng từ 1 đến 10 trong Bảng 4.
Bảng 3 – Ký hiệu và công bội của dãy số ưu tiên phụ
|
Ký hiệu dãy phụ |
Công bội của dãy |
|
|
Trị số quy tròn |
Trị số thực |
|
|
R80 |
1,03 |
|
|
R160 |
1,015 |
|
4.2. Ký hiệu dãy phụ có giới hạn tương tự như ký hiệu dãy cơ bản có giới hạn (xem 3.2).
5. Dãy dẫn xuất
Dãy dẫn xuất của số ưu tiên được lập bằng cách chọn mỗi số hạng thứ P của dãy cơ bản hoặc dãy phụ.
Ký hiệu dãy dẫn xuất bao gồm ký hiệu dãy tạo thành, gạch chéo phân cách và số 2, 3, 4, …, P tương ứng. Nếu dãy bị giới hạn thì trong ký hiệu phải có số hạng giới hạn dãy, nếu dãy không bị giới hạn thì phải ghi ít nhất một số hạng:
R5/2 (1… 1 000 000) – dãy dẫn xuất được lập từ mỗi số hạng thứ hai của dãy cơ bản R5 có giới hạn dưới là 1 và giới hạn trên là 1 000 000, bao gồm cả hai số hạng này;
R10/3 (… 80…) – dãy dẫn xuất được lập từ mỗi số hạng thứ ba của dãy cơ bản R10, có chứa số hạng 80 và không bị giới hạn ở cả hai phía;
R20/4 (112…) – dãy dẫn xuất được lập từ mỗi số hạng thứ tư của dãy cơ bản R20 và có giới hạn dưới là 112, bao gồm cả số hạng này;
R40/5 (… 60) – dãy dẫn xuất được lập từ mỗi số hạng thứ năm của dãy cơ bản R40 và có giới hạn trên là 60, bao gồm cả số hạng này.
5.3. Trong số những dãy dẫn xuất có cùng công bội, dãy nào có nhiều số hạng là lũy thừa nguyên của mười, sẽ được ưu tiên sử dụng. Nếu số những số hạng như vậy bằng nhau thì dãy nào có chứa 1 sẽ được ưu tiên sử dụng hơn.
Bảng 4 – Các số hạng của dãy số ưu tiên phụ
|
R80 |
R160 |
R80 |
R160 |
R80 |
R160 |
R80 |
R160 |
|
1,00 |
1,000 |
1,80 |
1,800 |
3,15 |
3,150 |
5,60 |
5,600 |
|
|
1,015 |
|
1,825 |
|
3,200 |
|
5,700 |
|
1,03 |
1,030 |
1,85 |
1,850 |
3,25 |
3,250 |
5,80 |
5,800 |
|
|
1,045 |
|
1,875 |
|
3,300 |
|
5,900 |
|
1,06 |
1,060 |
1,90 |
1,900 |
3,35 |
3,350 |
6,00 |
6,000 |
|
|
1,075 |
|
1,925 |
|
3,400 |
|
6,075 |
|
1,09 |
1,090 |
1,95 |
1,950 |
3,45 |
3,450 |
6,15 |
6,150 |
|
|
1,105 |
|
1,975 |
|
3,500 |
|
6,225 |
|
1,12 |
1,120 |
2,00 |
2,000 |
3,55 |
3,550 |
6.30 |
6,300 |
|
|
1,135 |
|
2,030 |
|
3,600 |
|
6,400 |
|
1,15 |
1,150 |
2,06 |
2,060 |
3,65 |
3,650 |
6,50 |
6,500 |
|
|
1,165 |
|
2,090 |
|
3,700 |
|
6,600 |
|
1,18 |
1,180 |
2,12 |
2,120 |
3,75 |
3,750 |
6,70 |
6,700 |
|
|
1,190 |
|
2,150 |
|
3,810 |
|
6,800 |
|
1,22 |
1,220 |
2,18 |
2,180 |
3,87 |
3,870 |
6,90 |
6,900 |
|
|
1,230 |
|
2,210 |
|
3,935 |
|
7,000 |
|
1,25 |
1,250 |
2,24 |
2,240 |
4,00 |
4,000 |
7,10 |
7,100 |
|
|
1,265 |
|
2,270 |
|
4,060 |
|
7,200 |
|
1,28 |
1,280 |
2,30 |
2,300 |
4,12 |
4,120 |
7,30 |
7,300 |
|
|
1,300 |
|
2,330 |
|
4,185 |
|
7,400 |
|
1,32 |
1,320 |
2,36 |
2,360 |
4,25 |
4,250 |
7,50 |
7,500 |
|
|
1,340 |
|
2,395 |
|
4,315 |
|
7,625 |
|
1,36 |
1,360 |
2,43 |
2,430 |
4,37 |
4,370 |
7,75 |
7,750 |
|
|
1,380 |
|
2,465 |
|
4,440 |
|
7,875 |
|
1,40 |
1,400 |
2,50 |
2,500 |
4,50 |
4,500 |
8,00 |
8,000 |
|
|
1,425 |
|
2,540 |
|
4,560 |
|
8,125 |
|
1,45 |
1,450 |
2,58 |
2,580 |
4,62 |
4,620 |
8,25 |
8,250 |
|
|
1,475 |
|
2,715 |
|
4,685 |
|
8,375 |
|
1,50 |
1,500 |
2,65 |
2,650 |
4,75 |
4,750 |
8,50 |
8,500 |
|
|
1,525 |
|
2,685 |
|
4,815 |
|
8,625 |
|
1,55 |
1,550 |
2,72 |
2,720 |
4,87 |
4,870 |
8,75 |
8,750 |
|
|
1,575 |
|
2,760 |
|
4,930 |
|
8,875 |
|
1,60 |
1,600 |
2,80 |
2,800 |
5,00 |
5,000 |
9,00 |
9,000 |
|
|
1,625 |
|
2,850 |
|
5,075 |
|
9,125 |
|
1,65 |
1,650 |
2,90 |
2,900 |
5,15 |
5,150 |
9,25 |
9,250 |
|
|
1,675 |
|
2,950 |
|
5,225 |
|
9,375 |
|
1,70 |
1,700 |
3,00 |
3,000 |
5,30 |
5,300 |
9,50 |
9,500 |
|
|
1,725 |
|
3,035 |
|
5,375 |
|
9,625 |
|
1,75 |
1,750 |
3,07 |
3,070 |
5,45 |
5,450 |
9,75 |
9,750 |
|
|
1,775 |
|
3,110 |
|
5,525 |
10,00 |
10,00 |
6. Dãy phối hợp
6.1. Dãy phối hợp của số ưu tiên được lập bằng cách phối hợp các dãy cơ bản và (hoặc) các dãy dẫn xuất khác nhau. Trong những khoảng thập phân khác nhau, dãy phối hợp có công bội khác nhau.
6.2. Khi lập dãy phối hợp phải hạn chế việc sử dụng nhiều dãy cơ bản và dãy dẫn xuất. Dãy phối hợp phải chứa ít nhất ba số hạng của mỗi dãy cơ bản và dãy dẫn xuất.
6.3. Những số hạng cuối và số hạng đầu của các dãy lập thành dãy phối hợp phải bằng nhau.
Ví dụ: R20 (1… 2) R10 (2… 10) R5/2 (10… 1 000).
7. Số ưu tiên quy tròn
Trong những trường hợp có đủ luận chứng, cho phép sử dụng các dãy số ưu tiên R’ và R” chứa những số ưu tiên quy tròn ghi trong Bảng 5 thay cho dãy cơ bản R của số ưu tiên.
Bảng 5 – Số ưu tiên quy tròn
|
R5 |
R’5 |
R10 |
R’10 |
R10 |
R20 |
R’20 |
R“20 |
R40 |
R’40 |
|
1,0 |
|
1,00 |
|
|
1,00 |
1,0 |
|
1,00 |
|
|
|
|
|
|
|
|
|
|
1,06 |
1,05 |
|
|
|
|
|
|
1,12 |
1,10 |
|
1,12 |
1,10 |
|
|
|
|
|
|
|
|
|
1,18 |
1,20 |
|
|
|
1,25 |
|
1,20 |
1,25 |
|
1,20 |
1,25 |
|
|
|
|
|
|
|
|
|
|
1,32 |
1,30 |
|
|
|
|
|
|
1,40 |
|
|
1,40 |
|
|
|
|
|
|
|
|
|
|
1,50 |
|
|
1,6 |
1,5 |
1,60 |
|
1,50 |
1,60 |
|
|
1,60 |
|
|
|
|
|
|
|
|
|
|
1,70 |
|
|
|
|
|
|
|
1,80 |
|
|
1,80 |
|
|
|
|
|
|
|
|
|
|
1,90 |
|
|
|
|
2,00 |
|
|
2,00 |
|
|
2,00 |
|
|
|
|
|
|
|
|
|
|
2,12 |
2,10 |
|
|
|
|
|
|
2,24 |
2,20 |
|
2,24 |
2,20 |
|
|
|
|
|
|
|
|
|
2,36 |
2,40 |
|
2,5 |
|
2,50 |
|
|
2,50 |
|
|
2,50 |
|
|
|
|
|
|
|
|
|
|
2,65 |
2,60 |
|
|
|
|
|
|
2,80 |
|
|
2,80 |
|
|
|
|
|
|
|
|
|
|
3,00 |
|
|
|
|
3,15 |
3,20 |
3,00 |
3,15 |
3,20 |
3,00 |
3,15 |
3,20 |
|
|
|
|
|
|
|
|
|
3,35 |
3,40 |
|
|
|
|
|
|
3,55 |
3,60 |
3,50 |
3,55 |
3,60 |
|
|
|
|
|
|
|
|
|
3,75 |
3,80 |
|
4,0 |
|
4,00 |
|
|
4,00 |
|
|
4,00 |
|
|
|
|
|
|
|
|
|
|
4,25 |
4,20 |
|
|
|
|
|
|
4,50 |
|
|
4,50 |
|
|
|
|
|
|
|
|
|
|
4,75 |
4,80 |
|
|
|
5,00 |
|
|
5,00 |
|
|
5,00 |
|
|
|
|
|
|
|
|
|
|
5,30 |
|
|
|
|
|
|
|
5,60 |
|
5,50 |
5,60 |
|
|
|
|
|
|
|
|
|
|
6,00 |
|
|
6,3 |
6,0 |
6,3 |
|
6,00 |
6,30 |
|
6,00 |
6,30 |
|
|
|
|
|
|
|
|
|
|
6,70 |
|
|
|
|
|
|
|
7,10 |
|
7,00 |
7,10 |
|
|
|
|
|
|
|
|
|
|
7,50 |
|
|
|
|
8,00 |
|
|
8,00 |
|
|
8,00 |
|
|
|
|
|
|
|
|
|
|
8,50 |
|
|
|
|
|
|
|
9,00 |
|
|
9,00 |
|
|
|
|
|
|
|
|
|
|
9,50 |
|
|
10,0 |
|
10,0 |
|
|
10,0 |
|
|
10,0 |
|
|
CHÚ THÍCH 1: Đối với các dãy R’ và R”, chỉ ghi những số hạng không trùng với những số hạng của dãy cơ bản R tương ứng. Trong khoảng từ 1 đến 10, dãy R“5 bao gồm các số hạng sau: 1,0; 2,5; 4,0; 6,0 và 10,0. Dãy R’10 đồng nhất với dãy R10, không kể số hạng 3,15 được thay bằng số hạng 3,20. CHÚ THÍCH 2: Trong những trường hợp đặc biệt, khi không cần quy định chặt chẽ cấp số nhân, khi cần sử dụng những trị số đơn giản để lập dãy, có thể chọn số 1,15 thay cho 1,18; 1,20 thay cho 1,25, để lập dãy trong khoảng 1; 1,05; 1,10; 1,15; 1,20; 1,30. |
|||||||||
7.2. Hạn chế tối đa việc sử dụng dãy R” và những số quy tròn của dãy. Chỉ được phép chuyển những số quy tròn của các dãy này vào trong khoảng thập phân lớn hơn 10 khi những số hạng ứng của các dãy cơ bản không là số nguyên.
7.3. Không cho phép đưa những số ưu tiên quy tròn vào các dãy R80 và R160.
Phụ lục A
(Tham khảo)
Hướng dẫn sử dụng số ưu tiên trong tính toán
Α.1. Những số hạng của cấp số cộng được lập từ số thứ tự của số ưu tiên (Bảng 2) là lôgarit cơ số ![]() của những số hạng của cấp số nhân tương ứng với những số ưu tiên của dãy R40.
của những số hạng của cấp số nhân tương ứng với những số ưu tiên của dãy R40.
Dãy số thứ tự có thể kéo dài về hai phía. Nếu Nn là số thứ tự của số ưu tiên n thì:
|
N1,00 = 0 |
N0,95 = -1 |
|
N1,06 = 1 |
N0,10 = – 40 |
|
N10 = 40 |
N0,01 = – 80 |
|
N100 = 80 |
|
Α.2. Tích hay thương của hai số ưu tiên n và n’ là số ưu tiên n“ được tính bằng cách cộng hoặc trừ những số thứ tự Nn và Nn’ và tìm số ưu tiên tương ứng với số thứ tự vừa nhận được.
|
VÍ DỤ 1: |
3,15 x 1,6 = 5 N3,15 + N1,16 = 20 + 8 = 28 = N5 |
|
VÍ DỤ 2: |
3 x 0,2 = 1,25 N6,3 + N0,2 = 32 + (-28) = 4 = N1,25 |
|
VÍ DỤ 3: |
1 : 0,06 = 17 N1 – N0,06 = 0 – (-49) = 49 = N17 |
Lũy thừa nguyên dương (hoặc âm) của một số ưu tiên nào đó là số ưu tiên được tính bằng cách nhân số thứ tự của số ưu tiên với số mũ của lũy thừa và tìm số ưu tiên tương ứng với số thứ tự vừa nhận được.
Căn hoặc lũy thừa phân số dương (hoặc âm) của một số ưu tiên nào đó là số ưu tiên được tính bằng cách tương tự, với điều kiện tích của số thứ tự và số mũ phân số của lũy thừa là một số nguyên.
|
VÍ DỤ 1: |
3,152 = 10 2 x N3,15 = 2 x 20 = 40 = N10 |
|
VÍ DỤ 2: |
|
|
VÍ DỤ 3: |
|
Ví dụ 4: ![]() không là số ưu tiên, bởi vì tích của số mũ của lũy thừa ¼ và số ưu tiên thứ tự 3 không là số nguyên.
không là số ưu tiên, bởi vì tích của số mũ của lũy thừa ¼ và số ưu tiên thứ tự 3 không là số nguyên.
|
VÍ DỤ 5: |
|
Phụ lục B
(Tham khảo)
Ví dụ sử dụng dãy số ưu tiên
B.1. Xác định sự phân cấp của các thông số khi những giá trị của chúng tiến tiệm cận đến giá trị giới hạn.
Đối với các thông số có giá trị tiến tiệm cận đến giá trị mong muốn tồn tại một cách khách quan, phải sử dụng số ưu tiên để xác định sai lệch của chúng so với giá trị mong muốn, chứ không phải xác định giá trị của các thông số. Những thông số như vậy ứng với, ví dụ, độ tinh khiết của chất tính bằng phần trăm.
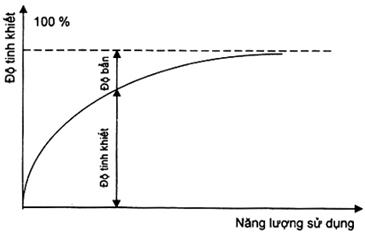
Sử dụng dãy R10 (… 20,0), chúng ta sẽ nhận được một loạt những giá trị về độ bẩn của chất như sau:
|
Độ bẩn, % |
20,0 |
16,0 |
12,5 |
10,0 |
8,00 |
6,30 |
5,00 |
4,00 |
3,15 |
… |
|
Độ tinh khiết, % |
80,0 |
84,0 |
87,5 |
90,0 |
92,00 |
93,70 |
95,00 |
96,00 |
96,85 |
… |
Có thể sử dụng dãy R”10 (… 20,0) chứa những số ưu tiên quy tròn thay cho dãy R10. Sử dụng dãy này, chúng ta sẽ nhận được một loạt những giá trị về độ bẩn của chất như sau:
|
Độ bẩn, % |
20,0 |
16,0 |
12,0 |
8,00 |
6,00 |
5,00 |
4,00 |
3,00 |
… |
|
Độ tinh khiết, % |
80,0 |
84,0 |
88,0 |
92,00 |
94,00 |
95,00 |
96,00 |
97,00 |
… |
B.2. Ưu tiên sử dụng dãy chứa nhiều lũy thừa nguyên của mười.
Số liệu cho trước:
Thông số: khối lượng
Khoảng phân cấp: từ 7,4 kg đến 21 kg
Mật độ phân cấp: 7 bậc trong giới hạn khoảng thập phân.
Lời giải:
Trị số thực công bội của dãy: ![]() .
.
Trị số quy tròn gần nhất: 1,18 (R40/3).
Phương án đáp số:
1) R40/3 (7,10… 23,6)
7,10; 8,50; 10,0; 11,8; 14,0; 17,0; 20,0; 23,6.
2) R40/3 (6,70… 22,4)
6,70; 8,00; 9,50; 11,2; 13,2; 16,0; 19,0; 22,4.
3) R40/3(6,30… 21.2)
6,30; 7,50; 9,00; 10,6; 12,5; 15,0; 18,0; 21,2.
Phương án 1 sẽ được chấp nhận vì có chứa số 10,0.


