Nội dung toàn văn Tiêu chuẩn Việt Nam TCVN 6910-5:2002 (ISO 5725-5 : 1998) về Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 5: các phương pháp khác xác định độ chụm của phương pháp đo tiêu chuẩn do Bộ Khoa học và Công nghệ ban hành
TIÊU CHUẨN VIỆT NAM
TCVN 6910-5 : 2002
ISO 5725-5 : 1998
ĐỘ CHÍNH XÁC (ĐỘ ĐÚNG VÀ ĐỘ CHỤM) CỦA PHƯƠNG PHÁP ĐO VÀ KẾT QUẢ ĐO – PHẦN 5: CÁC PHƯƠNG PHÁP KHÁC XÁC ĐỊNH ĐỘ CHỤM CỦA PHƯƠNG PHÁP ĐO TIÊU CHUẨN
Accuracy (trueness and precision) of measurement methods and results – Part 5: Alternative methods for the determination of the precision of a standard measurement method
Lời nói đầu
TCVN 6910-5:2002 hoàn toàn tương đương với ISO 5725-5 : 1998.
Phụ lục A của tiêu chuẩn này là quy định, các phụ lục B, C và D chỉ để tham khảo.
TCVN 6910-5 : 2002 do Tiểu ban Kỹ thuật Tiêu chuẩn TCVN/TC69/SC6 Phương pháp và Kết quả đo biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học Công nghệ ban hành.
Lời giới thiệu
0.0 TCVN 6910 – 5: 2002 là một phần của TCVN 6910, bộ tiêu chuẩn này gồm 6 phần dưới tên chung “Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo”:
– Phần 1: Nguyên tắc và định nghĩa chung
– Phần 2: Phương pháp cơ bản xác định độ lặp lại và độ tái lập của phương pháp đo tiêu chuẩn
– Phần 3: Các thước đo trung gian độ chụm của phương pháp đo tiêu chuẩn
– Phần 4: Các phương pháp cơ bản xác định độ đúng của phương pháp đo tiêu chuẩn
– Phần 5: Các phương pháp khác xác định độ chụm của phương pháp đo tiêu chuẩn
– Phần 6: Sử dụng các giá trị độ chính xác trong thực tế
0.1 TCVN 6910-5 (ISO 5725-5) sử dụng hai thuật ngữ “độ đúng” và “độ chụm” để mô tả độ chính xác của phương pháp đo. “Độ đúng” chỉ sự gần nhau giữa trung bình số học của một số lớn các kết quả thử nghiệm và giá trị thực hoặc giá trị quy chiếu được chấp nhận. “Độ chụm” chỉ sự gần nhau giữa các kết quả thử nghiệm
0.2. Việc khảo sát chung các đại lượng đó được thực hiện trong TCVN 6910-1 (ISO 5725-1) và vì vậy không được lặp lại ở đây. TCVN 6910-5 (ISO 5725-5) cần được đọc kết hợp với TCVN 6910-1 (ISO 5725-1), bởi vì các định nghĩa cơ bản và các nguyên tắc chung đã được nêu ra ở đó.
0.3 TCVN 6910-2 (ISO 5725-2) có liên quan tới việc ước lượng các thước đo tiêu chuẩn của độ chụm theo các thí nghiệm trong phòng thí nghiệm, như độ lệch chuẩn lặp lại và tái lập. TCVN 6910-2 (ISO 5725-2), nêu ra phương pháp cơ bản để ước lượng các đại lượng đó khi sử dụng thiết kế đồng mức. TCVN 6910-5 (ISO 5725-5) mô tả các phương pháp khác ngoài phương pháp cơ bản.
a) Phương pháp cơ bản có rủi ro khi một thao tác viên có thể cho phép kết quả đo của một phép đo trên một mẫu ảnh hưởng tới kết quả của một phép đo tiếp theo trên mẫu khác của cùng một loại vật liệu và điều đó gây ra các ước lượng chệch của độ lệch tiêu chuẩn lặp lại và tái lập. Khi rủi ro đó là trầm trọng, thiết kế mức tách biệt được mô tả trong tiêu chuẩn này có thể được ưa chuộng vì nó làm giảm độ rủi ro đó.
b) Phương pháp cơ bản cần phải chuẩn bị một số các mẫu vật liệu giống hệt nhau để dùng trong thí nghiệm. Với các vật liệu không đồng nhất điều đó là không thể được, như vậy việc sử dụng phương pháp cơ bản đó sẽ đưa ra các ước lượng vượt trội của độ lệch chuẩn tái lập do sự thay đổi giữa các mẫu. Thiết kế với các vật liệu không đồng nhất được nêu ra trong tiêu chuẩn này sẽ tạo ra thông tin về sự biến đổi giữa các mẫu mà nó không nhận được từ phương pháp cơ bản, có thể dùng thông tin đó để tính ước lượng của độ tái lập mà sự thay đổi giữa các mẫu đã bị loại bỏ.
c) Phương pháp cơ bản cần phải kiểm nghiệm các giá trị bất thường dùng để nhận ra các số liệu cần phải được loại bỏ khi tính các độ lệch chuẩn lặp lại và tái lập. Đôi khi việc loại bỏ các số liệu bất thường có hiệu quả lớn đối với các ước lượng của độ lệch chuẩn lặp lại và tái lập. nhưng trong thực tế khi áp dụng các phép kiểm nghiệm về giá trị bất thường, người phân tích số liệu cần phải xem xét để quyết định loại số liệu nào. Tiêu chuẩn này mô tả các phương pháp phân tích số liệu ổn định có thể dùng để tính các độ lệch chuẩn lặp lại và tái lập từ các số liệu có chứa các giá trị bất thường khi không sử dụng các phép kiểm nghiệm các giá trị bất thường để loại các số liệu đó, như vậy các kết quả không nhất thiết bị ảnh hưởng bởi sự xét đoán của người phân tích số liệu.
ĐỘ CHÍNH XÁC (ĐỘ ĐÚNG VÀ ĐỘ CHỤM) CỦA PHƯƠNG PHÁP ĐO VÀ KẾT QUẢ ĐO – PHẦN 5: CÁC PHƯƠNG PHÁP KHÁC XÁC ĐỊNH ĐỘ CHỤM CỦA PHƯƠNG PHÁP ĐO TIÊU CHUẨN
Accuracy (trueness and precision) of measurement methods and results – Part 5: Alternative methods for the determination of the precision of a standard measurement method
1. Phạm vi áp dụng
Tiêu chuẩn này nhằm
– Mô tả một cách chi tiết các phương pháp khác với phương pháp cơ bản để xác định độ lệch chuẩn lặp lại và tái lập của một phương pháp đo tiêu chuẩn, đó là việc thiết kế mức tách biệt và thiết kế với các vật liệu không đồng nhất:
– Mô tả việc sử dụng các phương pháp ổn định để phân tích các kết quả của các thí nghiệm về độ chụm khi không sử dụng các thử nghiệm bất thường nhằm loại bỏ các số liệu khi tính toán và đặc biệt là mô tả việc sử dụng cụ thể một phương pháp như vậy.
Tiêu chuẩn này nhằm bổ sung cho TCVN 6910-2 (ISO 5725-2) bằng cách đưa ra các thiết kế khác mà trong một số tình huống chúng có thể có giá trị hơn so với thiết kế cơ bản nêu trong TCVN 6910-2 (ISO 5725-2), đưa ra một phương pháp phân tích ổn định để thu được các ước lượng của độ lệch chuẩn lặp lại và tái lập mà chúng phụ thuộc ít hơn vào sự xét đoán của người phân tích dữ liệu số với các ước lượng thu được bằng các phương pháp đã mô tả trong TCVN 6910-2 (ISO 5725-2).
2. Tiêu chuẩn viện dẫn
ISO 3534-1:1993. Statistics – Vocabulary and symbols – Part 1: Probability and general statistical term (Thống kê học – Từ vựng và kí hiệu – Phần 1: Thuật ngữ xác suất và thống kê chung)
ISO 3534-3:1995. Statistics – Vocabulary and symbols – Part 3: Design of experiments (Thống kê học – Từ vựng và kí hiệu – Phần 3: Thiết kế thí nghiệm)
TCVN 6910-1: 2001 (ISO 5725-1:1994). Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 1 Nguyên tắc và định nghĩa chung
TCVN 6910-2: 2001 (ISO 5725-2:1994), Độ chính xac (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 2: Phương pháp cơ bản xác định độ lặp lại và độ tái lập của phương pháp đo tiêu chuẩn
3. Định nghĩa
Tiêu chuẩn này sử dụng các định nghĩa đã nêu ra trong ISO 3534 – 1 và TCVN 6910-1 (ISO 5725-1).
Các ký hiệu dùng trong TCVN 6910 được trình bày trong phụ lục A.
4. Thiết kế mức tách biệt
4.1. Các ứng dụng của thiết kế mức tách biệt
4.1.1. Thiết kế đồng mức được mô tả trong TCVN 6910-2 (ISO 5725-2) cần phải có hai hoặc nhiều hơn các mẫu thử giống hệt nhau của một vật liệu thử trong mỗi phòng thí nghiệm tham gia và ở mỗi mức thí nghiệm. Với thiết kế này có thể có rủi ro như sau: một thao tác viên có thể cho phép kết quả đo trên một mẫu ảnh hưởng tới kết quả đo của lần đo tiếp theo trên một mẫu khác với cùng vật liệu. Nếu điều đó xẩy ra các kết quả thí nghiệm của độ chụm sẽ bị sai lệch: các ước lượng sr của độ lệch chuẩn lặp lại sẽ giảm đi và các ước lượng của độ lệch chuẩn giữa các phòng thí nghiệm sL sẽ tăng lên. Trong thiết kế mức tách biệt, mỗi phòng thí nghiệm tham gia được cung cấp một mẫu với một trong hai vật liệu tương tự ở mỗi mức của thí nghiệm và những người thao tác được thông báo rằng các mẫu đó là không đồng nhất, nhưng họ không được thông báo các vật liệu đó khác nhau như thế nào. Như vậy việc thiết kế mức tách biệt nêu ra một phương pháp để xác định độ lệch chuẩn lặp lại và tái lập của một phương pháp đo tiêu chuẩn nhằm giảm thiểu sự rủi ro do một kết quả thử nghiệm trên một mẫu sẽ ảnh hưởng tới một kết quả thử nghiệm trên một mẫu khác trong thí nghiệm.
4.1.2. Các số liệu thu được ở một mức của thí nghiệm mức tách biệt có thể sử dụng để vẽ đồ thị, trong đó các số liệu của một vật liệu được vẽ thành biểu đồ so với số liệu của một vật liệu tương tự khác. Ví dụ vẽ biểu đồ như vậy được cho trong hình 1. Các đồ thị như vậy giúp cho việc nhận ra phòng thí nghiệm nào có độ chệch lớn nhất so với các phòng thí nghiệm khác. Điều này rất có ích khi nghiên cứu các nguyên nhân của độ chệch phòng thí nghiệm lớn nhất nhằm tiến hành việc hiệu chỉnh.
4.1.3. Nói chung các độ lệch chuẩn lặp lại và tái lập của một phương pháp đo phụ thuộc vào mức của vật liệu. Ví dụ, khi kết quả thử nghiệm là tỷ lệ của một thành phần thu được trong phân tích hóa học, độ lệch chuẩn lặp lại và tái lập thông thường tăng lên khi tỷ lệ của yếu tố đó tăng. Đối với một thí nghiệm mức tách biệt, hai vật liệu tương tự sử dụng ở một mức thí nghiệm cần phải giống nhau đến mức để hy vọng có thể thu được các độ lệch chuẩn lặp lại và tái lập như nhau. Với thiết kế mức tách biệt, hai vật liệu ở một mức thí nghiệm là chấp nhận được nếu chúng dẫn đến gần như cùng một mức của các kết quả đo còn việc sắp xếp các vật liệu khác nhau một cách đáng kể sẽ không mang lại kết quả gì.
Trong nhiều phương pháp phân tích hóa học, mẫu hỗn hợp gồm các chất cấu thành có thể ảnh hưởng đến độ chụm, do vậy đối với thí nghiệm mức tách biệt cần phải có hai vật liệu với các mẫu hỗn hợp giống nhau ở mỗi mức của thí nghiệm. Đôi khi có thể chuẩn bị vật liệu tương đối giống nhau bằng cách cho thêm vào chất đó một lượng nhỏ chất cấu thành. Khi vật liệu là vật liệu tự nhiên hoặc được chế tạo, khó có thể tìm được hai sản phẩm đủ giống nhau cho mục đích của thí nghiệm mức tách biệt: một giải pháp khả dĩ là có thể sử dụng hai mẻ của cùng một sản phẩm. Cần phải nhớ rằng mục đích của việc chọn các vật liệu cho thiết kế mức tách biệt là cung cấp cho thao tác viên các mẫu mà họ không thể nhận biết được.
4.2. Bố trí thiết kế mức tách biệt
4.2.1. Việc bố trí thiết kế mức tách biệt được chỉ ra trong bảng 1.
p phòng thí nghiệm tham gia mỗi thử nghiệm hai mẫu ở q mức.
Hai mẫu trong một mức được ký hiệu bởi a và b, trong đó a biểu thị mẫu của một vật liệu, b biểu thị mẫu của một vật liệu tương tự khác.
4.2.2. Các số liệu từ một thí nghiệm mức tách biệt được biểu diễn bởi
yijk
trong đó
chỉ số i biểu thị phòng thí nghiệm thứ i (i = 1, 2, 3,.. ,p);
chỉ số j biểu thị mức thứ j (j = 1, 2, 3,…..,q):
chỉ số k biểu thị mẫu k (k = a hoặc b).
4.3. Tổ chức thí nghiệm mức tách biệt
4.3.1. Theo hưóng dẫn trong điều 6 của TCVN 6910-1: 2001 (ISO 5725-1:1994) khi lập kế hoạch thí nghiệm mức tách biệt.
Trong 6.3 của TCVN 6910-1: 2001 (ISO 5725-1:1994) có một số công thức (trong đó có đại lượng thường được ký hiệu bởi A) được sử dụng để giúp quyết định xem cần phải có bao nhiêu phòng thí nghiệm tham gia thí nghiệm đó. Các công thức tương ứng cho thí nghiệm mức tách biệt được nêu dưới đây.
Chú thích – Các công thức này đã được dẫn ra bằng phương pháp đã mô tả trong phần chú thích 24 của TCVN 6910-1: 2001 (ISO 5725-1:1994).
Để đánh giá độ không đảm bảo của các ước lượng của độ lệch chuẩn lặp lại và tái lập hãy tính các đại lượng sau:
Đối với độ lặp lại:

Đối với độ tái lập:
![]() với
với
với
![]()
Nếu số lần lặp lại n được lấy bằng 2 trong phương trình (9) và (10) của TCVN 6910-1: 2001 (ISO 5725-1: 1994) thì có thể thấy rằng các phương trình (9) và (10) trong TCVN 6910-1:2001 (ISO 5725-1: 1994) chính là các phương trình (1) và (2) ở trên, chỉ khác là ở đây đôi khi p -1 thay cho p trong TCVN 6910-1: 2001 (ISO 5725-1:1994). Đó chỉ là một sự khác nhau nhỏ. Như vậy bảng 1 và các hình B.1 và B.2 của TCVN 6910-1: 2001 (ISO 5725-1:1994) có thể được sử dụng để đánh giá độ không đảm bảo của ước lượng của độ lệch chuẩn lặp lại và tái lập trong thí nghiệm mức tách biệt.
Để xác định độ không đảm bảo của ước lượng độ chệch của phương pháp đo trong thí nghiệm mức tách biệt tính đại lượng A xác định bởi phương trình (13) của TCVN 6910-1: 2001 (ISO 5725-1:1994) với n = 2 (hoặc sử dụng bảng 2 của TCVN 6910-1:2001 (ISO 5725-1:1994) và sử dụng đại lượng này như đã mô tả trong TCVN 6910-1 (ISO 5725-1)
Để xác định độ không đảm bảo của ước lượng độ chệch phòng thí nghiệm trong thí nghiệm mức tách biệt, tính đại lượng Aw theo phương trình (16) của TCVN 6910-1:2001 (ISO 5725-1:1994) với n = 2. Vì số lần lặp lại trong thí nghiệm mức tách biệt trên thực tế là 2, nên không thể giảm bớt độ không đảm bảo của ước lượng độ chệch phòng thí nghiệm bằng cách tăng số lần lặp lại. (Nếu cần giảm bớt độ không đảm bảo đó cần phải sử dụng thiết kế đồng mức).
4.3.2. Cần tuân theo hướng dẫn trong điều 5. 6 của TCVN 6910-2:2001 (ISO 5725-2:1994) và chú ý đến các chi tiết trong việc tổ chức thí nghiệm mức tách biệt. Số lần lặp lại n trong TCVN 6910-2 (ISO 5725-2): có thể lấy bằng số các mức tách biệt trong thiết kế mức tách biệt, tức là bằng 2.
Các mẫu a và b cần phải được phân một cách ngẫu nhiên cho những người tham gia với thao tác ngẫu nhiên riêng biệt.
Trong thí nghiệm mức tách biệt cần phải thông báo cho các chuyên gia thống kê biết khi nào các số liệu được ghi lại, kết quả nào đã nhận được trên vật liệu a, kết quả nào trên vật liệu b ở mỗi mức thí nghiệm. Dán nhãn các mẫu nếu có thể được và phải cẩn trọng không để tiết lộ thông tin cho những người tham gia.
Bảng 1 – Biểu mẫu nên dùng để tập hợp số liệu đối với thiết kế mức tách biệt
|
Phòng thí nghiệm |
Mức |
|||||||||
|
1 |
2 |
|
j |
|
q |
|||||
|
a |
b |
a |
b |
|
a |
b |
|
a |
b |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
4.4. Mô hình thống kê
4.4.1. Mô hình cơ bản dùng trong tiêu chuẩn này được cho trong điều 5 của TCVN 6910-1:2001 (ISO 5725-1:1994). Để ước lượng độ chính xác (độ đúng và độ chụm) của phương pháp đo, thường giả thiết rằng mỗi kết quả đo là tổng của ba thành phần:
(3)
trong đó, đối với một vật liệu cụ thể được thử nghiệm:
mj biểu thị trung bình chung ở mức cụ thể j = 1,…., q;
Bij là biểu thị thành phần phòng thí nghiệm của độ chệch trong các điều kiện lặp lại ở một phòng thí nghiệm cụ thể i = 1,…..p, ở một mức cụ thể j = 1….., q;
eijk biểu thị sai số ngẫu nhiên của kết quả thử nghiệm k = 1.2….. n. nhận được trong phòng thí nghiệm i ở mức j dưới điều kiện lặp lại:
4.4.2. Đối với thí nghiệm mức tách biệt mô hình đó trở thành:
(4)
Phương trình này khác với phương trình (3) trong 4.4.1 ở chỗ chỉ số k trong mjk có nghĩa là theo phương trình (4) trung bình chung ở mức j bây giờ có thể phụ thuộc vào vật liệu a hoặc vật liệu b (k = 1,2).
Sự vắng mặt của chỉ số k trong Bij có nghĩa là người ta giả thiết rằng độ chệch gắn với phòng thí nghiệm i không phụ thuộc vào vật liệu a hoặc b trong một mức. Điều này giải thích tại sao hai vật liệu phải là giống nhau.
4.4.3. Xác định trung bình ô như sau:
![]()
và độ sai khác theo ô (hiệu số ô) như sau:
![]()
4.4.4. Trung bình chung cho một mức j của một thí nghiệm mức tách biệt có thể được xác định như sau:
![]()
4.5. Phân tích thống kê các số liệu từ thí nghiệm mức tách biệt
4.5.1. Tập hợp các số liệu thành một bảng như đã chỉ ra trong bảng 1. Mỗi sự kết hợp một phòng thí nghiệm với một mức tạo ra một “ô” trong bảng đó chứa hai thánh phần của số liệu, yija và yijb.
Tính các độ sai khác theo ô Dij và đưa chúng vào bảng như đã chỉ ra trong bảng 2. Phương pháp phân tích đó đòi hỏi phải tính mỗi độ sai khác theo cùng một cách
a – b
và dấu của hiệu số đó cần được ghi lại.
Tính các trung bình ô y và đưa chúng vào một bảng như đã chỉ ra trong bảng 3.
4.5.2. Nếu một ô trong bảng 1 không chứa hai kết quả thử nghiệm (ví dụ: vì các mẫu đã bị hỏng hoặc các số liệu đã bị loại ra sau khi áp dụng các phép thử về giá trị bất thường sẽ được miêu tả dưới đây) thì các ô tương ứng trong bảng (2) và (3) đều là ô trống.
4.5.3. Với mỗi mức j của thí nghiệm, tính giá trị trung bình Dj và độ lệch chuẩn sDj của các độ sai khác trong cột j của bảng 2:

Trong đó tổng S lấy theo tất cả các phòng thí nghiệm i = 1,2,….,p.
Nếu có các ô trống trong bảng 2, thì p là số các ô có chứa số liệu trong cột j của bảng 2 và tổng được thực hiện trên tất cả các ô không trống.
4.5.4. Với mỗi mức j của thí nghiệm tính giá trị trung bình yj và độ lệch chuẩn syj của giá trị trung bình ô trong cột thứ j của bảng 3:

Trong đó tổng S lấy theo tất cả các phòng thí nghiệm i = 1,2,…..,p.
Nếu có các ô trống trong bảng 3, thì p là số các ô có chứa số liệu trong cột j của bảng 3 và tổng được thực hiện trên tất cả các ô không trống.
4.5.5. Sử dụng bảng 2 và 3 và các thống kê được tính trong 4.5.3 và 4.5.4 để kiểm tra tính phù hợp và tính bất thường của số liệu như sẽ được mô tả trong 4.6. Nếu các số liệu bị loại bỏ, tính lại các thống kê đó.
4.5.6. Tính độ lệch chuẩn lặp lai srj và độ lệch chuẩn tái lặp sR từ các công thức:

4.5.7. Nghiên cứu xem srj và sRJ có phụ thuộc vào giá trị trung bình yj hay không, nếu có phải xác định mối quan hệ hàm bằng cách sử dụng các phương pháp đã được mô tả trong 7.5 của TCVN 6910-2: 2001
Bảng 2 – Biểu mẫu nên dùng để lập bảng các độ sai khác theo ô đối với thiết kế mức tách biệt
|
Phòng thí nghiệm |
Mức |
|||||
|
1 |
2 |
|
j |
|
q |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
Bảng 3 – Biểu mẫu nên dùng để lập bảng các giá trị trung bình ô đối với thiết kế mức tách biệt
|
Phòng thí nghiệm |
Mức |
|||||
|
1 |
2 |
|
j |
|
q |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
4.6. Khảo sát sự phù hợp và bất thường của các số liệu
4.6.1. Để kiểm tra sự phù hợp của các số liệu người ta dùng các thống kê h đã được mô tả trong 7.3.1 của TCVN 6910-2:2001 (ISO 5725-2:1994).
Để kiểm tra sự phù hợp của các độ sai khác theo ô, tính các thống kê h như sau:
![]()
Để kiểm tra sự phù hợp của các trung bình ô, tính các thống kê h như sau
![]()
Để chỉ ra các phòng thí nghiệm không phù hợp, vẽ biểu đồ cả hai tập thống kê đó theo thứ tự của các mức, nhưng gộp lại theo phòng thí nghiệm, như đã được chỉ ra trong hình 2 và 3. Việc giải thích các đồ thị đó sẽ được đề cập đến một cách đầy đủ trong 7.3.1 của TCVN 6910-2:2001 (ISO 5725-2:1994). Nếu một phòng thí nghiệm có độ lặp lại xấu hơn các phòng thí nghiệm khác thì nó được thể hiện bởi một số lượng lớn khác thường các thống kê h có giá trị lớn trên đồ thị được vẽ từ các độ sai khác theo ô. Nếu phòng thí nghiệm đưa ra các kết quả chệch thì điều đó được thể hiện bởi sự biến thiên theo một hướng của các thống kê h trên đồ thị được dựng lên từ các trung bình ô. Trong các trường hợp như vậy phải yêu cầu các phòng thí nghiệm đó nghiên cứu và báo cáo những sai sót của những người tổ chức thí nghiệm.
4.6.2. Kiểm tra các số liệu tản mạn và bất thường bằng phép kiểm nghiệm Grubb, đã được mô tả trong 7.3.4. của TCVN 6910-2 2001 (ISO 5725-2:1994)
Để kiểm nghiệm giá trị tản mạn và bất thường của các độ sai khác theo ô, áp dụng phép kiểm nghiệm Grubb đối với các giá trị trong mỗi cột của bảng 2.
Để kiểm nghiệm các giá trị tản mạn và bất thường của các giá trị trung bình theo ô, áp dụng phép kiểm nghiệm Grubb đối với các giá trị trong mỗi cột của bảng 3.
Các phép kiểm nghiệm đó đã được giải thích một cách đầy đủ trong 7.3.2 của TCVN 6910-2:2001 (ISO 5725-2:1994). Chúng được dùng để phát hiện các kết quả không phù hợp với các kết quả còn lại của các số liệu ghi được trong thí nghiệm, mà dựa trên các số liệu đó các kết luận rút ra từ việc tính độ lệch chuẩn lặp lại và tái lập sẽ ảnh hưởng đến các giá trị của các thống kê đó một cách thực chất. Thông thường các số liệu tỏ ra là bất thường sẽ bị loại ra khi tính toán và các số liệu tản mạn vẫn được đưa vào, trừ khi có đủ lý do để loại. Nếu các phép kiểm nghiệm chỉ ra rằng một giá trị ở trong bảng 2 hoặc bảng 3 bị loại khi tính toán độ lệch chuẩn lặp lại và tái lập thì giá trị tương ứng trong bảng kia cũng bị loại.
4.7. Báo cáo kết quả của thí nghiệm mức tách biệt
4.7.1. Khuyến nghị được đưa ra trong 7.7 của TCVN 6910-2:2001 (ISO 5725-2:1994) về:
– báo cáo kết quả của việc phân tích thống kê cho hội đồng chuyên môn;
– các quyết định của hội đồng; và
– việc chuẩn bị báo cáo đầy đủ.
4.7.2. Các khuyến nghị về hình thức công bố về độ lệch chuẩn lặp lại và tái lập của một phương pháp đo tiêu chuẩn được trình bày trong 7.1 của TCVN 6910-1:2001 (ISO 5725-1:1994).
4.8. Ví dụ 1: Thí nghiệm mức tách biệt – Xác định protein
4.8.1. Bảng 4 bao gồm các số liệu từ thí nghiệm [5] để xác định hàm lượng protein trong thức ăn bằng cách đốt cháy. Có chín phòng thí nghiệm tham gia và thí nghiệm bao gồm 14 mức. Trong mỗi mức sử dụng hai phần thức ăn có tỷ lệ khối lượng protein như nhau.
4.8.2. Bảng 5 và 6 đưa ra trung bình và độ sai khác theo ô đã được tính toán như mô tả trong 4.5.1, cho mức 14 (j = 14) của thí nghiệm.
Sử dụng phương trình (8) và (9) trong 4.5.3, đối với sự sai khác trong bảng 5 thu được:
D14 = 8,34 %
sD14 = 0,4361 %
và áp dụng phương trình (10) và (11) trong 4.5.4 đối với các giá trị trung bình ô trong bảng 6 thu được:
y14 = 85,46 %
sy14 = 0,4534 %
như vậy độ lệch chuẩn lặp lại và tái lập khi sử dụng các phương trình (12) và (13) trong 4.5.6 sẽ là:
sr14 = 0,31 %
sR14 = 0,50 %
Bảng 7 đưa ra các kết quả tính toán cho các mức khác nhau.
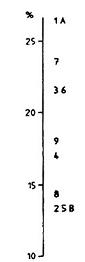
4.8.3. Hình 1 trình bày “biểu đồ Youden”’ cho mẫu a tương ứng với mẫu b ở mức 14 trong bảng 4. Phòng thí nghiệm 5 cho một điểm ở góc trái phía dưới của đồ thị, phòng thí nghiệm 1 cho một điểm ở góc phải phía trên. Điều đó chứng tỏ rằng các số liệu của phòng thí nghiệm 5 có độ chệch âm và các số liệu của phòng thí nghiệm 1 có độ chệch dương trên cả hai mẫu a và b. Điều đó thường thấy khi vẽ biểu đồ các số liệu từ một thiết kế mức tách biệt như hình 1. Hình đó cũng chỉ ra rằng các kết quả của phòng thí nghiệm 4 là không bình thường, vì một điểm đối với phòng thí nghiệm này nằm cách xa đường trung bình của hai mẫu đó. Các phòng thí nghiệm khác tạo nên một nhóm ở giữa biểu đồ. Như vậy hình này nêu ra một trường hợp để nghiên cứu những nguyên nhân của các độ chệch ở ba phòng thí nghiệm đó.
Chú thích – Để có thêm thông tin khác về “biểu đồ Youden” xem các tài liệu tham khảo [7] và (8).
4.8.4. Giá trị của các thống kê h ở mức 14, được tính như trong 4.6.1, chỉ ra trong bảng 5 và 6. Các giá trị cho tất cả các mức được vẽ thành biểu đồ trong hình 2 và 3.
Trong hình 3, thống kê h đối với các trung bình theo ô chứng tỏ rằng phòng thí nghiệm 5 cho các thống kê h âm ở tất cả các mức và điều này thể hiện rõ độ chệch âm nhất quán với các số liệu của chúng. Cũng trong hình đó các phòng thí nghiệm 8 và 9 cho các thống kê h hầu như tất cả đều là dương chứng tỏ rằng có độ chệch dương nhất quán với các số liệu của chúng (nhưng nhỏ hơn độ chệch âm trong phòng thí nghiệm 5). Cũng như vậy các thống kê h đối với các phòng thí nghiệm 1, 2 và 6 thể hiện một độ chệch biến đổi theo mức trong mỗi phòng thí nghiệm đó. Sự tương tác như vậy giữa các phòng thí nghiệm và các mức có thể cung cấp các đầu mối về nguyên nhân của các độ chệch phòng thí nghiệm.
Hình 2 không thể hiện một kiểu dáng nào đáng chú ý
4.8.5. Các giá trị của thống kê Grubb được cho trong bảng 8. Các phép kiểm nghiệm đó chứng tỏ rằng các số liệu từ phòng thí nghiệm 5 là đáng nghi ngờ.
4.8.6. Ở giai đoạn này của việc phân tích, chuyên gia thống kê cần bắt đầu khảo sát các nguyên nhân gây ra số liệu nghi ngờ ở phòng thí nghiệm 5 trước khi tiến hành phân tích số liệu. Nếu không phát hiện được các nguyên nhân đó có khi phải loại tất cả các số liệu từ phòng thí nghiệm 5 khi tính độ lệch chuẩn lặp lại và tái lập. Sau đó tiếp tục sự phân tích bằng việc khảo sát các mối quan hệ hàm số có thể có giữa độ lệch chuẩn lặp lại và tái lập và trung bình chung. Trong TCVN 6910-2 (ISO 5725-2): chưa đề cập đến vấn đề nào liên quan tới điều này và như vậy nó chưa được xét ở đây.
Bảng 4 – Ví dụ 1: Xác định tỷ lệ khối lượng protein trong thức ăn, theo %
|
Phòng thí nghiệm |
Mức |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
||||||||||
|
a |
b |
a |
b |
a |
b |
a |
b |
a |
b |
|||||
|
1 |
11,11 |
10,34 |
10,91 |
9,81 |
13,74 |
13,48 |
13,79 |
13,00 |
15,89 |
15,26 |
||||
|
2 |
11,12 |
9,94 |
11,38 |
10,31 |
14,00 |
13,12 |
13,44 |
13,06 |
15,69 |
15,10 |
||||
|
3 |
11,26 |
10,46 |
10,95 |
10,51 |
13,38 |
12,70 |
13,54 |
13,18 |
15,83 |
15,73 |
||||
|
4 |
11,07 |
10,41 |
11,66 |
9,95 |
13,01 |
13,16 |
13,58 |
12,88 |
15,08 |
15,63 |
||||
|
5 |
10,69 |
10,31 |
10,98 |
10,13 |
13,24 |
13,33 |
13,32 |
12,59 |
15,02 |
14,90 |
||||
|
6 |
11,73 |
11,01 |
12,31 |
10,92 |
14,01 |
13,66 |
14,04 |
13,64 |
16,43 |
15,94 |
||||
|
7 |
11,13 |
10,36 |
11,38 |
10,44 |
12,94 |
12,44 |
13,63 |
13,06 |
15,75 |
15,56 |
||||
|
8 |
11,21 |
10,51 |
11,32 |
10,84 |
13,09 |
13,76 |
13,85 |
13,49 |
15,98 |
15,89 |
||||
|
9 |
11,80 |
11,21 |
11,35 |
9,88 |
13,85 |
14,46 |
13,96 |
13,77 |
16,51 |
15,72 |
||||
|
Phòng thí nghiệm |
Mức |
|||||||||||||
|
6 |
7 |
8 |
9 |
10 |
||||||||||
|
a |
b |
a |
b |
a |
b |
a |
b |
a |
b |
|||||
|
1 |
20,14 |
19,78 |
20,33 |
20,06 |
46,45 |
44,42 |
52,05 |
49,40 |
65,84 |
59,14 |
||||
|
2 |
19,25 |
20,25 |
20,36 |
19,94 |
46,69 |
44,62 |
51,94 |
48,81 |
66,31 |
59,19 |
||||
|
3 |
20,48 |
19,86 |
20,56 |
20,11 |
46,90 |
44,56 |
52,18 |
48,90 |
66,06 |
58,52 |
||||
|
4 |
21,54 |
20,06 |
20,64 |
20,46 |
47,13 |
45,29 |
51,73 |
48,56 |
65,93 |
58,93 |
||||
|
5 |
19,90 |
19,66 |
20,56 |
19,24 |
45,83 |
43,73 |
50,84 |
47,91 |
64,19 |
57,94 |
||||
|
6 |
20,31 |
20,27 |
20,85 |
20,63 |
40,86 |
43,96 |
52,18 |
49,03 |
65,73 |
58,77 |
||||
|
7 |
20,00 |
20,56 |
20,25 |
20,19 |
46,25 |
44,31 |
52,25 |
49,44 |
66,06 |
59,19 |
||||
|
8 |
20,43 |
20,69 |
20,85 |
20,27 |
47,11 |
44,40 |
52,44 |
48,81 |
65,66 |
59,38 |
||||
|
9 |
20,64 |
21,01 |
20,78 |
20,89 |
47,09 |
45,15 |
52,19 |
48,46 |
66,33 |
59,47 |
||||
|
Phòng thí nghiệm |
Mức |
|||||||||||||
|
11 |
12 |
13 |
14 |
|
||||||||||
|
a |
b |
a |
b |
a |
b |
a |
b |
|
|
|||||
|
1 |
84,16 |
80,86 |
85,38 |
81,71 |
87,64 |
88,23 |
90,24 |
82,10 |
|
|
||||
|
2 |
84,50 |
81,06 |
85,56 |
82,44 |
88,81 |
88,38 |
89,88 |
81,44 |
|
|
||||
|
3 |
82,26 |
79,43 |
85,26 |
82,15 |
88,58 |
88,12 |
89,48 |
81,67 |
|
|
||||
|
4 |
84,39 |
80,08 |
85,20 |
81,76 |
88,47 |
87,98 |
90,04 |
80,73 |
|
|
||||
|
5 |
81,71 |
79,01 |
83,58 |
79,74 |
86,43 |
86,19 |
88,59 |
80,46 |
|
|
||||
|
6 |
82,85 |
81,16 |
84,44 |
80,90 |
87,78 |
86,89 |
89,40 |
80,88 |
|
|
||||
|
7 |
86,25 |
81,00 |
84,88 |
81,44 |
88,06 |
88,00 |
89,31 |
81,38 |
|
|
||||
|
8 |
84,59 |
81,16 |
84,96 |
81,71 |
88,50 |
87,98 |
89,94 |
81,56 |
|
|||||
|
9 |
83,05 |
80,93 |
84,73 |
81,94 |
88,24 |
88,05 |
89,75 |
81,35 |
|
|
||||
|
Bảng 5 – Ví dụ 1: Độ sai khác theo ô ở mức 14 |
|
Bảng 6 – Ví dụ 1: Trung bình ô ở mức 14 |
||||
|
Phòng thí nghiệm |
Độ sai khác trong ô % |
Thống kê h |
|
Phòng thí nghiệm |
Độ sai khác trong ô % |
Thống kê h |
|
1 |
8,14 |
-0,459 |
|
1 |
86,170 |
1,576 |
|
2 |
8,44 |
0,229 |
|
2 |
85,660 |
0,451 |
|
3 |
7,81 |
– 1,215 |
|
3 |
85,575 |
0,263 |
|
4 |
9,31 |
2,224 |
|
4 |
85,385 |
– 0,156 |
|
5 |
8,13 |
– 0,482 |
|
5 |
84,525 |
– 2,052 |
|
6 |
8,52 |
0,413 |
|
6 |
85,140 |
– 0,696 |
|
7 |
7,93 |
– 0,940 |
|
7 |
85,345 |
– 0,244 |
|
8 |
8,38 |
0,092 |
|
8 |
85,750 |
0,649 |
|
9 |
8,40 |
0,138 |
|
9 |
85,550 |
0,208 |
Bảng 7 – Ví dụ 1: Giá trị của các trung bình, độ sai khác trung bình và độ lệch chuẩn tính từ các số liệu ở tất cả 14 mức trong bảng 4
|
Mức j |
Số lượng phòng thí nghiệm r |
Trung bình chung yj% |
Độ sai khác trung bình Dj% |
Độ lệch chuẩn
|
|||
|
Syj % |
sDj% |
srj % |
sRj % |
||||
|
1 |
9 |
10,87 |
0,73 |
0,35 |
0,21 |
0,15 |
0,36 |
|
2 |
9 |
10,84 |
1,05 |
0,36 |
0,43 |
0,30 |
0,42 |
|
3 |
9 |
13,11 |
0,13 |
0,44 |
0,55 |
0,39 |
0,52 |
|
4 |
9 |
13,43 |
0,50 |
0,30 |
0,21 |
0,15 |
0,32 |
|
5 |
9 |
15,66 |
0,27 |
0,39 |
0,40 |
0,29 |
0,44 |
|
6 |
9 |
20,27 |
0,06 |
0,40 |
0,73 |
0,52 |
0,54 |
|
7 |
9 |
20,39 |
0,38 |
0,30 |
0,41 |
0,29 |
0,37 |
|
8 |
9 |
45,60 |
2,21 |
0,44 |
0,37 |
0,26 |
0,47 |
|
9 |
9 |
50,40 |
3,16 |
0,44 |
0,35 |
0,25 |
0,47 |
|
10 |
9 |
62,37 |
6,84 |
0,53 |
0,40 |
0,28 |
0,57 |
|
11 |
9 |
82,14 |
3,23 |
1,01 |
1,08 |
0,77 |
1,15 |
|
12 |
9 |
83,17 |
3,45 |
0,74 |
0,46 |
0,33 |
0,77 |
|
13 |
9 |
87,91 |
0,30 |
0,69 |
0,41 |
0,29 |
0,72 |
|
14 |
9 |
85,46 |
8,34 |
0,45 |
0,44 |
0,31 |
0,50 |
Bảng 8 – Ví dụ 1: Giá trị của các thống kê Grubb
|
Thống kê Grubb cho các độ sai khác |
||||
|
Mức |
Một giá trị nhỏ nhất |
Hai giá trị nhỏ nhất |
Hai giá trị lớn nhất |
Một giá trị lớn nhất |
|
1 |
1,653 |
0,5081 |
0,3139 |
2,125 |
|
2 |
1,418 |
0,3945 |
0,4738 |
1,535 |
|
3 |
1,462 |
0,3628 |
0,5323 |
1,379 |
|
4 |
1,490 |
0,5841 |
0,4771 |
1,414 |
|
5 |
2,033 |
0,3485 |
0,6075 |
1,289 |
|
6 |
1,456 |
0,5490 |
0,3210 |
1,947 |
|
7 |
1,185 |
0,6820 |
0,1712 |
2,296* (5) |
|
8 |
0,996 |
0,7571 |
0,1418* (6; 8) |
1,876 |
|
9 |
1,458 |
0,5002 |
0,3092 |
1,602 |
|
10 |
1,474 |
0,3360 |
0,4578 |
1,737 |
|
11 |
1,422 |
0,5089 |
0,2943 |
1,865 |
|
12 |
1,418 |
0,6009 |
0,2899 |
1,956 |
|
13 |
2,172 |
0,2325 |
0,6326 |
1,444 |
|
14 |
1,215 |
0,6220 |
0,2362 |
2,224* (4) |
Thống kê Grubb cho các trung bình ô
|
Mức |
Một giá trị nhỏ nhất |
Hai giá trị nhỏ nhất |
Hai giá trị lớn nhất |
Một giá trị lớn nhất |
|
1 |
1,070 |
0,6607 |
0,1291* (6 : 9) |
1,832 |
|
2 |
1,318 |
0,6288 |
0,2118 |
2,165 |
|
3 |
1,621 |
0,4771 |
0,4077 |
1,680 |
|
4 |
1,591 |
0,5339 |
0,3807 |
1,429 |
|
5 |
1,794 |
0,4018 |
0,5009 |
1,333 |
|
6 |
1.291 |
0,4947 |
0,4095 |
1,386 |
|
7 |
1,599 |
0,5036 |
0,4391 |
1,470 |
|
8 |
1,872 |
0,3753 |
0,4536 |
1,404 |
|
9 |
2,328* (5) |
0,1317* (4 : 5) |
0,7417 |
1,025 |
|
10 |
2,456** (5) |
– |
– |
1,000 |
|
11 |
1,756 |
0,2469 |
0,5759 |
1,472 |
|
12 |
2,037 |
0,1063* (5 : 6) |
0,7116 |
1,130 |
|
13 |
2,308* (5) |
0,0733* (5 : 6) |
0,7777 |
0,994 |
|
14 |
2,052 |
0,2781 |
0,5486 |
1,576 |
|
Chú thích – Số trong ngoặc đơn biểu thị các phòng thí nghiệm đưa ra các giá trị tản mạn hoặc bất thường Giá trị tới hạn của các thống kê kiểm nghiệm Grubb cho 9 phòng thí nghiệm, áp dụng cho các độ sai khác hoặc các trung bình ô, như sau: |
||||
|
|
Giá trị tản mạn (*) |
Giá trị bất thường (**) |
||
|
Phép kiểm nghiệm Grubb cho một giá trị bất thường đơn lẻ |
2.215 |
2.387 |
||
|
Phép kiểm nghiệm Grubb cho một cặp các giá trị bất thường |
0,1492 |
0,0851 |
||
|
|
||||

Hình 1 – Ví dụ 1: Các số liệu thu được ở mức 14
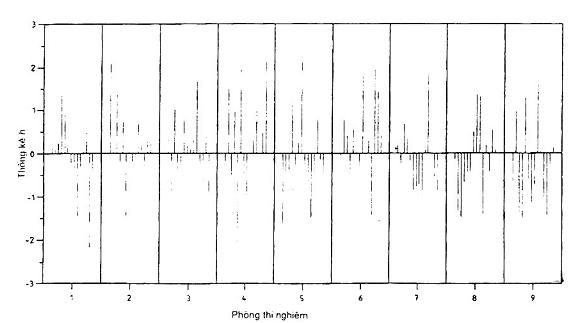
Hình 2 – Ví dụ 1: Kiểm tra sự phù hợp của các độ sai khác theo ô
(gộp lại theo phòng thí nghiệm)
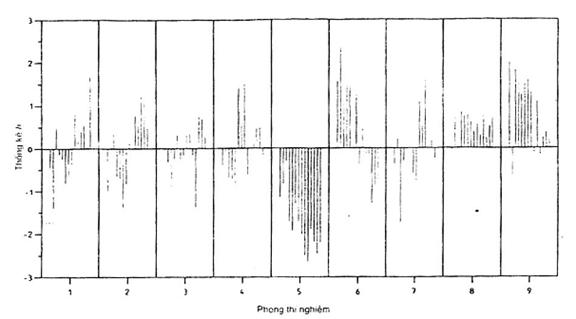
Hình 3 – Ví dụ 1: Kiểm tra sự phù hợp trên các trung bình ô
(gộp lại theo phòng thí nghiệm)
5. Thiết kế cho các vật liệu không đồng nhất
5.1. Ứng dụng các thiết kế cho các vật liệu không đồng nhất
5.1.1. Một ví dụ về vật liệu không đồng nhất là da thuộc. Không có hai miếng da nào là giống hệt nhau và các tính chất của da thuộc thực chất thay đổi trong một miếng da. Một kiểm nghiệm thông thường đối với da thuộc là kiểm nghiệm về độ bền kéo đứt theo BS 3144[3]. Điều đó được thực hiện trên các mẫu thử dạng cặp đôi. (BS 3144 quy định số các mẫu thử như vậy được cắt từ một miếng da cũng như vị trí và hướng của chúng trong miếng da, như vậy việc định nghĩa tự nhiên về “mẫu” để dùng khi kiểm nghiệm da thuộc là một miếng da hoàn chỉnh). Nếu một thí nghiệm về độ chụm được thực hiện khi sử dụng thiết kế đồng mức như được mô tả trong TCVN 6910-2 (ISO 5725-2), mỗi phòng thí nghiệm được gửi tới một mảnh da ở mỗi mức của thí nghiệm và thu được hai kết qua thử nghiệm trên mỗi miếng da. Sự thay đổi giữa các miếng da cộng thêm với sự thay đổi giữa các phòng thí nghiệm như vậy sẽ làm gia tăng độ lệch chuẩn tái lập. Tuy nhiên nếu mỗi phòng thí nghiệm được gửi tới hai miếng da ở mỗi mức, và hai kết quả thử nghiệm thu được trên mỗi mảnh da, thì các số liệu có thể được dùng để ước lượng sự thay đổi giữa các miếng da và để tính các giá trị cho độ lệch chuẩn tái lập của phương pháp thử nghiệm trong đó sự thay đổi giữa các miếng da đã được loại bỏ.
5.1.2. Một ví dụ khác về vật liệu không đồng nhất là cát (có thể được dùng làm bê tông). Dưới tác động của gió và nước, cát nằm theo các tầng chứa các hạt biến đổi dần theo cỡ của các hạt. Như vậy khi cát được sử dụng, phân bố cỡ hạt luôn luôn được quan tâm. Trong kỹ thuật, phân bố cỡ hạt của cát được đo bằng thử nghiệm sàng lọc (ví dụ BS 812-103[1]). Để kiểm nghiệm cát, một mẫu chung được lấy ra từ một sản phẩm, sau đó một hoặc một số mẫu thử được tạo ra từ mẫu chung. Thông thường mẫu chung có khối lượng vào khoảng 10 kg và các mẫu thử vào khoảng 200 g. Vì sự thay đổi tự nhiên của vật liệu, luôn luôn có sự khác nhau giữa các mẫu chung của cùng một sản phẩm. Do đó cũng như với da thuộc nếu thực hiện một thí nghiệm đồng mức, trong đó mỗi phòng thí nghiệm được gửi một mẫu chung ở mỗi mức, sự thay đổi giữa các mẫu chung sẽ làm gia tăng độ lệch chuẩn tái lập tính toán của phương pháp thử nghiệm, nhưng nếu các phòng thí nghiệm được gửi tới hai mẫu chung ở mỗi mức thì giá trị của các độ lệch chuẩn tái lập có thể tính được và loại bỏ được sự thay đổi đó.
5.1.3. Các ví dụ trên cùng thể hiện rõ các đặc tính khác của các vật liệu không đồng nhất: vì sự thay đổi của vật liệu, việc chuẩn bị các mẫu thử hoặc lô thử có thể là một nguồn quan trọng của sự thay đổi. Như đối với da thuộc, quá trình cắt các mẫu thử từ một miếng da có thể ảnh hưởng lớn đến độ dài có thể kéo được và với các thử nghiệm sàng lọc trên cát quá trình chuẩn bị các mẫu thử từ mẫu chung thường là những nguồn thay đổi chủ yếu trong phương pháp thử nghiệm. Nếu mẫu hoặc các mẫu thử được chuẩn bị cho thí nghiệm về độ chụm không tương ứng đối với thực tế thông thường (cố gắng tạo ra các mẫu đồng nhất), thì các giá trị của độ lệch chuẩn lặp lại và tái lập được tạo ra bởi thí nghiệm đó sẽ không thể hiện được sự thay đổi diễn ra trong thực tế. Có những tình huống trong đó người ta mong muốn tạo ra các mẫu đồng nhất bằng một quá trình được thiết kế đặc biệt để loại bỏ càng nhiều càng tốt sự thay đổi của vật liệu ( ví dụ đối với sự thử nghiệm về độ thành thạo hoặc khi một thí nghiệm về độ chụm được sử dụng như là một phần của chương trình làm việc trong khi triển khai một phương pháp đo). Tuy nhiên, khi mục tiêu của thí nghiệm về độ chụm là phát hiện sự thay đổi sẽ diễn ra trong thực tế (ví dụ khi người bán và người mua kiểm nghiệm các mẫu của cùng một sản phẩm), sự thay đổi do tính không đồng nhất của vật liệu cần được bao gồm trong các số đo về độ chụm của phương pháp đo.
Cần phải thận trọng để đảm bảo rằng mỗi kết quả thử nghiệm trong một thí nghiệm thu được bằng cách thực hiện một quy trình thử nghiệm là độc lập với các kết quả thử nghiệm khác. Điều này sẽ không còn đúng nếu một số giai đoạn chuẩn bị mẫu thử bị chia sẻ bởi nhiều mẫu, đến nỗi độ chệch hoặc độ lệch nảy sinh ra từ sự chuẩn bị đó sẽ có ảnh hưởng chung đến các kết quả kiểm nghiệm từ các mẫu thử.
5.1.4. Việc thiết kế các vật liệu không đồng nhất được đề xuất trong điều này tạo ra các thông tin về sự thay đổi giữa các mẫu mà không thể thu được từ thiết kế đồng mức được mô tả trong TCVN 6910 -2. Có một phí tổn không thể tránh được để nhận được thông tin phụ thêm: thiết kế đề suất cần có nhiều mẫu hơn để thử nghiệm. Các thông tin phụ thêm này có thể có giá trị. Trong ví dụ về da thuộc ở 5.1.1, thông tin về sự thay đổi giữa các miếng da có thể được sử dụng để quyết định xem bao nhiêu miếng da cần phải kiểm nghiệm khi đánh giá chất lượng của mẫu gửi tới hoặc để quyết định giữa hai sự lựa chọn: kiểm nghiệm nhiều miếng da với ít mẫu thử trên một miếng hoặc kiểm nghiệm ít miếng da với nhiều mẫu thử trên một miếng. Trong ví dụ về cát ở 5.1.2, thông tin về sự thay đổi giữa các mẫu cát có thể được dùng để quyết định xem thủ tục tiến hành lấy mẫu có thỏa đáng chưa hay cần phải có sự cải tiến.
5.1.5. Thiết kế được mô tả trong điều này áp dụng được đối với các thí nghiệm bao gồm ba yếu tố được sắp xếp theo thứ bậc: yếu tố “các phòng thí nghiệm” ở mức cao nhất, yếu tố “các mẫu trong phòng thí nghiệm” ở mức sau và yếu tố “kết quả thử nghiệm trong các mẫu” ở mức thấp nhất. Một trường hợp khác có thể gặp phải trong thực tế là trường hợp xếp thứ bậc ba yếu tố: “phòng thí nghiệm” ở mức cao nhất, “các kết quả thử nghiệm trong các phòng thí nghiệm” ở mức sau. “sự xác định giá trị trong các kết quả thử nghiệm” ở mức thấp nhất. Điều này sẽ xuất hiện nếu các phòng thí nghiệm tham gia trong thí nghiệm về độ chụm được gửi tới một mẫu đơn lẻ của một vật liệu đồng nhất và yêu cầu phải thực hiện hai (hoặc có thể nhiều hơn) phép thử nghiệm trên mẫu và mỗi phép thử nghiệm gồm một số lần xác định giá trị và kết quả thử nghiệm cần tính là trung bình của các lần xác định. Các công thức cho trong 5.5, 5.6 và 5.9 có thể được áp dụng cho các số liệu thu được trong một thí nghiệm như vậy, nhưng các độ lệch chuẩn lặp lại và tái lập cần phải được tính theo cách khác hơn một chút so với cách nêu ra ở đây (xem chú thích 2 của 5.5.5). Cần định rõ số lần xác định giá trị khi tính trung bình để đưa ra một kết quả thử nghiệm, vì điều này ảnh hưởng tới giá trị của các độ lệch chuẩn lặp lại và tái lập.
5.2. Bố trí thiết kế các vật liệu không đồng nhất
5.2.1. Việc bố trí thiết kế các vật liệu không đồng nhất được trình bày trong bảng 9.
Mỗi phòng trong p phòng thí nghiệm tham gia được cung cấp hai mẫu ở q mức và thu được hai kết quả thử nghiệm trên mỗi mẫu. Mỗi ô như vậy trong thí nghiệm chứa bốn kết quả thử nghiệm (hai kết quả đối với mỗi mẫu).
Có thể mở rộng thiết kế đơn giản đó bằng cách cho phép có nhiều hơn hai mẫu trong một phòng thí nghiệm ở mỗi mức hoặc có nhiều hơn hai kết quả thử nghiệm trên mỗi mẫu. Việc tính toán thiết kế mở rộng phức tạp hơn nhiều so với thiết kế với hai kết quả thử nghiệm trên một mẫu và hai mẫu trên một phòng thí nghiệm ở mỗi mức. Tuy nhiên các nguyên tắc thiết kế mở rộng giống hệt như các nguyên tắc thiết kế đơn giản. Vì vậy những tính toán sẽ được thiết lập chi tiết ở trong điều này cho thiết kế đơn giản. Các công thức để tính toán giá trị của độ lệch chuẩn lặp lại và tái lập với thiết kế mở rộng và ví dụ áp dụng sẽ được đưa ra trong 5.9 và 5.10 dưới đây.
5.2.2. Các số liệu từ thiết kế vật liệu không đồng nhất được biểu thị bởi
yijtk
trong đó
chỉ số i biểu thị phòng thí nghiệm (i = 1…. p’)
chỉ số j biểu thị mức (j = 1.2,…., q).
chỉ số t biểu thị mẫu (t = 1 .2,…., g)
chỉ số k biểu thị kết quả thử nghiệm (k = 1, 2,…., n).
Thông thường g = 2, n = 2. trong thiết kế mở rộng cả hai số g hoặc n đều lớn hơn 2.
Chú thích – Trong TCVN 6910 -1 và TCVN 6910-2 (ISO 5725-2), p được dùng để biểu thị số các phòng thí nghiệm cũng như chỉ số trong các bảng các giá trị tới hạn đối với phép kiểm nghiệm Cochran: Với thiết kế đồng mức cả hai số là như nhau. Với thiết kế với các vật liệu không đồng nhất chỉ số đối với phép kiểm nghiệm Cochran có thể là bội số của số các phòng thí nghiệm. Vì vậy ở đây p’ dùng để chỉ số lượng các phòng thí nghiệm còn p biểu thị chỉ số đối với phép kiểm nghiệm Cochran.
5.3. Tổ chức thí nghiệm với vật liệu không đồng nhất
5.3.1. Phải tuân theo hướng dẫn đã nêu trong điều 6 của TCVN 6910 -1: 2001 khi thiết kế thí nghiệm với vật liệu không đồng nhất, cần xét thêm các vấn đề sau:
Cần phải chuẩn bị bao nhiêu mẫu cho mỗi phòng thí nghiệm ở mỗi mức?
Thông thường, vì phải tính đến chi phí nên số mẫu cần chuẩn bị là hai.
Có thể sử dụng các công thức, bảng, hình vẽ trong điều 6 và phụ lục B của TCVN 6910 -1: 2001 để chọn số các phòng thí nghiệm, số mẫu và số lần lặp lại, nhưng với sự cải biên sẽ được thiết lập trong 5.3.2 và 5.3.5.
5.3.2. Có thể đánh giá độ không đảm bảo của ước lượng độ lệch chuẩn lặp lại và tái lập từ một thí nghiệm trên vật liệu không đồng nhất bằng cách tính đại lượng Ar như đã trình bầy trong 6.3 của TCVN 6910 -1: 2001 (ISO 5725-1:1994):
![]()
thay cho đại lượng được xác định bởi phương trình (9) của TCVN 6910 -1: 2001 . Tuy nhiên có thể dẫn ra phương trình trên bằng cách thay p bởi p’x g trong phương trình (9) của TCVN 6910-1: 2001 (ISO 5725- 1:1994). Do đó trong TCVN 6910-1: 2001 (ISO 5725-1:1994), hình B1 và các đại lượng cho độ lặp lại dưới dạng Ar trong bảng 1 có thể sử dụng được bằng cách đưa vào hình vẽ hoặc bảng với p =p’ x g. Như vậy nói chung khi g = 2 các mẫu được chuẩn bị cho mỗi phòng thí nghiệm ở mỗi mức sẽ đưa vào bảng hoặc hình vẽ trong TCVN 6910-1 (ISO 5725-1) với p = 2p’.
Chú thích – Công thức cho Ar ở trên ( và AR dưới đây) đã được dẫn ra theo phương pháp đã mô tả trong chú thích 24 của 6910 – 1: 2001.
5.3.3. Có thể đánh giá độ không đảm bảo của ước lượng độ lệch chuẩn lặp lại và tái lập từ một thí nghiệm trên một vật liệu không đồng nhất bằng cách tính đại lượng AR như đã được trình bày trong 6.3 của TCVN 6910-1: 2001 (ISO 5725-1: 1994) như sau:
![]()
thay cho đại lượng được xác định bởi phương trình (10) trong TCVN 6910-1: 2001 (ISO 5725-1:1994).
Trong đó:

Có thể dẫn ra các giá trị của F và g từ các ước lượng sơ bộ của các đô lệch chuẩn sH, sR và sr thu được trong quá trình chuẩn hóa phương pháp đo.
5.3.4. Chú ý tới hướng dẫn được đưa ra trong điều 5 và 6 của TCVN 6910-2:2001 (ISO 5725-2:1994) với việc xem xét các chi tiết về tổ chức thí nghiệm với vật liệu không đồng nhất.
Điều 5.1.2 của TCVN 6910-2:2001 (ISO 5725-2:1994) bao gồm các yêu cầu “một nhóm gồm n thử nghiệm” hoặc “một nhóm gồm n lần đo” ( ví dụ một nhóm gồm n thử nghiệm cần phải được tiến hành với các điều kiện lặp lại). Trong một thí nghiệm với vật liệu không đồng nhất, các yêu cầu đó có liên quan tới nhóm gồm g x n thử nghiệm trong một ô, tức là liên quan tới tất cả các thử nghiệm trong một phòng thí nghiệm ở một mức.
Trong thí nghiệm với vật liệu không đồng nhất, số các mẫu cần phải chuẩn bị ở mỗi mức là p’ x g (tức là 2p‘ khi g = 2 trong trường hợp bình thường). Điều quan trọng là phải phân bố p’ x g mẫu đó một cách ngẫu nhiên cho các phòng thí nghiệm tham gia.
5.4. Mô hình thống kê cho một thí nghiệm với vật liệu không đồng nhất
5.4.1. Mô hình cơ bản được dùng trong tiêu chuẩn này chính là phương trình (3) trong 4.4.1 đã được trình bày lại. Đối với một thí nghiệm với vật liệu không đồng nhất mô hình đó được mở rộng thành
![]()
Các số hạng m, B và e có cùng ý nghĩa như trong phương trình (3) trong 4.4.1. Nhưng phương trình (19) còn có thêm số hạng Hijt biểu thị sự thay đổi giữa các mẫu và chỉ số t biểu thị các mẫu trong các phòng thí nghiệm (ý nghĩa của các chỉ số khác đã được nêu ra trong 5.2.2)
Giả thiết sau đây là hợp lý sự thay đổi giữa các mẫu là ngẫu nhiên và không phụ thuộc vào phòng thí nghiệm, nhưng có thể phụ thuộc vào mức thí nghiệm, như vậy số hạng Hijt trung bình bằng không và phương sai được cho bởi:
![]()
5.4.2. Đối với trường hợp thông thường với hai mẫu trong một phòng thí nghiệm và hai kết quả thử nghiệm trên một mẫu (g = n = 2), ta xác định:
a) Trung bình mẫu, phạm vi giữa các kết quả thử nghiệm cho phòng thí nghiệm i, mức j và mẫu t (t= 1 hoặc 2)

b) Trung bình ô và phạm vi giữa các mẫu cho phòng thí nghiệm i và mức j

c) Trung bình chung, độ lệch chuẩn của các trung bình ô cho mức j

trong đó tổng được lấy theo các phòng thí nghiệm i = 1,2,…..,p’.
5.5. Phân tích thống kê các số liệu của một thí nghiệm với vật liệu không đồng nhất
5.5.1. Ở đây khảo sát chi tiết trường hợp thông thường khi hai mẫu được chuẩn bị cho mỗi phòng thí nghiệm ở mỗi mức và trên mỗi mẫu thu được hai kết quả thử nghiệm. (Trường hợp tổng quát sẽ được khảo sát ở 5.9 và 5.10).
Tập hợp các số liệu thành bảng như đã chỉ ra trong bảng 9. Mỗi sự kết hợp của một phòng thí nghiệm và một mức sẽ cho một “ô” trong bảng này, mỗi ô chứa bốn kết quả thử nghiệm.
Sử dụng các phương trình (21) đến (26) trong 5.4.2:
a) tính các phạm vi giữa kết quả thử nghiệm và đưa chúng vào một bảng như bảng 10
b) tính các phạm vi giữa các mẫu và đưa chúng vào một bảng như bảng 11
c) tính các giá trị trung bình ô và đưa chúng vào một bảng như bảng 12
Ghi lại các phạm vi như là các giá trị dương (không kể dấu).
Bảng 9 – Biểu mẫu nên dùng để tập hợp các số liệu của thiết kế cho vật liệu không đồng nhất
|
Phòng thí nghiệm |
Mẫu |
Mức 1 |
Mức 2 |
|
Mức j |
|
Mức q |
||||
|
Số các kết quả thử nghiệm |
|||||||||||
|
1 |
2 |
1 |
2 |
|
1 |
2 |
|
1 |
2 |
||
|
1 |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
p’ |
1 2 |
|
|
|
|
|
|
|
|
|
|
Bảng 10 – Biểu mẫu nên dùng để lập bảng các phạm vi giữa các kết quả thử nghiệm cho thiết kế với vật liệu không đồng nhất
|
Phòng thí nghiệm |
Mẫu |
Mức 1 |
Mức 2 |
|
Mức j |
|
Mức q |
|
1 |
1 2 |
|
|
|
|
|
|
|
2 |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
1 2 |
|
|
|
|
|
|
|
p’ |
1 2 |
|
|
|
|
|
|
Bảng 11 – Biểu mẫu nên dùng để lập bảng các phạm vi giữa các mẫu cho thiết kế với vật liệu không đồng nhất
|
Phòng thí nghiệm |
Mức 1 |
Mức 2 |
|
Mức j |
|
Mức q |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p’ |
|
|
|
|
|
|
Bảng 12 – Biểu mẫu nên dùng để lập bảng các trung bình ô cho thiết kế với vật liệu không đồng nhất
|
Phòng thí nghiệm |
Mức 1 |
Mức 2 |
|
Mức j |
|
Mức q |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p’ |
|
|
|
|
|
|
5.5.2. Nếu một ô trong bảng 9 chứa ít hơn bốn kết quả thử nghiệm (ví dụ do mẫu bị hỏng hoặc các số liệu đã bị loại ra khi áp dụng các phép thử về giá trị bất thường sẽ được mô tả dưới dây) thì:
a) hoặc sử dụng công thức cho trường hợp tổng quát được nêu ra về sau…
b) hoặc bỏ qua tất cả các số liệu trong ô.
Lựa chọn a) được ưa chuộng hơn. Lựa chọn b) lãng phí số liệu nhưng cho phép sử dụng công thức đơn giản.
5.5.3. Với mỗi mức j của thí nghiệm tính các đại lượng sau
a) Tổng các bình phương của các phạm vi giữa các kết quả thử nghiệm trong cột j của bảng 10 (lấy tổng trên p’ phòng thí nghiệm và trên 2 mẫu)

b) Tổng các bình phương các phạm vi giữa các mẫu trong cột j của bảng 11 (lấy tổng trên p’ phòng thí nghiệm)
![]()
c) Trung bình và độ lệch chuẩn của các trung bình ô trong cột j của bảng 12, khi sử dụng phương trình (25) và (26) trong 5.4.2.
5.5.4. Sử dụng bảng 10, 11 và 12 và tính toán các thống kê trong 5.5.3 để kiểm tra sự phù hợp và bất thường của các số liệu như đã mô tả trong 5.6. Nếu bất kỳ số liệu nào bị loại bỏ cần tính lại các thống kê đó.
5.5.5. Tính toán các độ lệch chuẩn lặp lại sr và độ lệch chuẩn tái lập sRj từ:
![]()
![]()
nếu xẩy ra
![]()
thì xác định
![]()
Tính một ước lượng sHj của độ lệch chuẩn mà nó đo sự biến đổi giữa các mẫu như sau:
![]()
Chú thích
1) Nên thực hiện việc kiểm nghiệm về ý nghĩa để thấy rõ sự thay đổi giữa các mẫu là có ý nghĩa về mặt thống kê hay không. Tuy nhiên điều đó không phải là một phần cần thiết của việc phân tích. Việc sử dụng phép kiểm nghiệm đó để quyết định xem sự thay đổi giữa các mẫu có thể bỏ qua được hay không (tức là quyết định xem các kết quả kiểm nghiệm trong mỗi ô có được xử lý như khi tất cả chúng nhận được trên cùng một mẫu hay không trong việc pnân tích là điều không đúng. Điều này có thể dẫn đến độ chệch trong việc ước lượng độ lệch chuẩn lặp lại, bởi vì việc phát hiện sự biến đổi giữa các mẫu là không có ý nghĩa về mặt thống kê không chứng tỏ rằng sự thay đổi giữa các mẫu là không đáng kể.
2) Trong trường hợp đã mô tả ở 5.1.5 (khi ba yếu tố là “phòng thí nghiệm”, “các thử nghiệm trong phòng thí nghiệm”, “xác định giá trị trong các thử nghiệm”) độ lệch chuẩn lặp lại và tái lập cần được tính như sau:

Các công thức này được áp dụng khi các kết quả thử nghiệm là trung bình của hai lần xác định giá trị.
5.5.6. Nghiên cứu xem srj, và sRj có phụ thuộc vào trung bình chung yj hay không, nếu phụ thuộc, hãy xác định quan hệ hàm số đó bằng cách sử dụng phương pháp đã nêu trong 7.5 của TCVN 6910-2:2001 (ISO 5725-2:1994)
5.6. Khảo sát sự phù hợp và sự bất thường của các số liệu
5.6.1. Sử dụng các thông kê h và k như đã mô tả trong 7.3.1 của TCVN 6910-2:2001 (ISO 5725- 2:1994)
Để kiểm tra sự phù hợp của các trung bình ô, tính thống kê h như sau:
![]()
Vẽ biểu đồ các giá trị thống kê đó theo thứ tự các mức, nhưng gộp lại theo phòng thí nghiệm để chỉ ra phòng thí nghiệm không phù hợp.
Để kiểm tra sự phù hợp của các phạm vi giữa các mẫu, tính các giá trị thống kê k như sau:
![]()
Vẽ biểu đồ các giá trị thống kê đó theo thứ tự các mức, nhưng gộp lại theo phòng thí nghiệm để chỉ ra phòng thí nghiệm không phù hợp
Để kiểm tra sự phù hợp của các phạm vi giữa các kết quả thử nghiệm, tính các giá trị thống kê k như sau:
![]()
Vẽ biểu đồ các giá trị thống kê đó theo thứ tự các mức, nhưng gộp lại theo phòng thí nghiệm để chỉ ra phòng thí nghiệm không phù hợp.
Việc giải thích các đồ thị đó được bàn đến một cách đầy đủ trong 7.3.1 của TCVN 6910-2:2001 (ISO 5725-2:1994) Nếu một phòng thí nghiệm báo cáo các kết quả nói chung bị chệch, thì hầu hết các thống kê h đối với phòng thí nghiệm đó sẽ lớn và theo cùng một hướng được thể hiện trong đồ thị lập nên từ các trung bình ô. Nếu một phòng thí nghiệm không thực hiện việc thử nghiệm trong các mức với các điều kiện lặp lại (và cho phép các nhân tố lạ làm tăng thêm sự thay đổi giữa các mẫu) thì các thống kê k với các giá trị lớn khác thường sẽ hiện rõ trên đồ thị được dựng lên từ các phạm vi giữa các mẫu. Nếu một phòng thí nghiệm có độ lặp lại xấu thì nó sẽ đưa ra các thống kê k với các giá trị lớn khác thường được hiện rõ trên đồ thị được dựng lên từ các phạm vi giữa các kết quả thử nghiệm.
5.6.2. Sử dụng phép kiểm nghiệm Cochran như được mô tả trong 7.3.3 và 7.3.4 của TCVN 6910- 2:2001 (ISO 5725-2:1994) để kiểm tra sự tản mạn và bất thường của các số liệu.
Để kiểm tra sự tản mạn và bất thường của các phạm vi giữa các kết quả thử nghiệm, tính giá trị thống kê Cochran cho mỗi mức j:
![]()
trong đó wmax là giá trị lớn nhất của các phạm vi giữa các kết quả thử nghiệm wijt cho mức j.
Để sử dụng bảng các giá trị tới hạn trong 8.1 của TCVN 6910-2:2001 (ISO 5725-2:1994) tra bảng đó theo hàng ứng với p = 2p’ theo rìa biên bên trái và theo cột có đầu đề n = 2.
Để kiểm nghiệm các giá trị tản mạn và bất thường theo các phạm vi giữa các mẫu, tính giá trị thống kê Cochran cho mỗi mức j:
![]()
trong đó wmax là giá trị lớn nhất trong số các phạm vi giữa các mẫu wij đối với mức j.
Để sử dụng các giá trị tới hạn trong TCVN 6910-2:2001 (ISO 5725-2:1994) tra bảng đó theo hàng ứng với p = p’ theo rìa biên bên trái và theo cột có đầu đề n = 2.
Để kiểm nghiệm các giá trị tản mạn và bất thường theo các trung bình ô, ta tính giá trị thống kê Grubb từ các trung bình ô như đã chỉ ra trong 7.3.4 của TCVN 6910-2:2001 (ISO 5725-2:1994) cho mỗi mức j (trong đó s trong TCVN 6910-2: 2001 (ISO 5725-2: 1994) chính là syjđược xác định bởi phương trình (26) trong 5.4.2)
Việc diễn giải các phép kiểm nghiệm đó được thảo luận một cách đầy đủ trong 7.3.2 của TCVN 6910- 2:2001 (ISO 5725-2:1994). Trong thí nghiệm với vật liệu không đồng nhất, các kết quả của việc áp dụng các phép kiểm nghiệm đó cần phải tiến hành theo thứ tự sau đây. Trước tiên cần áp dụng phép kiểm nghiệm Cochran đối với các phạm vi giữa các kết quả trung bình. Dựa trên phép kiểm nghiệm đó nếu quyết định rằng một phạm vi giữa các kết quả thử nghiệm là bất thường và bị loại bỏ, thì hai kết quả thử nghiệm xác định phạm vi bất thường đó cũng cần phải được loại bỏ khi tính độ lệch chuẩn lặp lại và tái lập (nhưng các kết quả thử nghiệm khác trong ô vẫn cần phải được giữ lại). Tiếp theo hãy áp dụng phép kiểm nghiệm Cochran đối với các phạm vi giữa các mẫu và cuối cùng áp dụng phép kiểm nghiệm Grubb đối với các trung bình ô. Nếu quyết định rằng một phạm vi giữa các mẫu là bất thường hoặc một trung bình ô là bất thường và rằng các kết quả gây ra những bất thường như vậy cần loại bỏ, thì cùng loại bỏ tất cả các kết quả đối với các ô tương ứng khi tính độ lệch chuẩn lặp lại và tái lập.
5.7. Báo cáo kết quả của một thí nghiệm trên vật liệu không đồng nhất
Các tài liệu tham khảo đưa ra trong 4.7 cũng áp dụng cho thí nghiệm trên các vật liệu không đồng nhất.
5.8. Ví dụ 2: Thí nghiệm trên vật liệu không đồng nhất
5.8.1. Tập hợp vật chất được sử dụng làm vật liệu (lớp bê tông hoặc bitum) để tạo nên bề mặt của các phi trường và các xa lộ cần phải có khả năng chịu thấm nước và chống đóng băng. Phương pháp thường dùng để đo khả năng đó là phương pháp thử nghiệm về sự không bị hư hỏng bởi sunphat manhê [2] trong đó một mẫu thử của tập hợp chất bị nhúng vào dung dịch sunphát manhê bão hòa và sau đó được làm khô một số lần. Ban đầu mẫu thử được chuẩn bị sao cho tất cả các hạt của tập hợp vật chất đều được giữ lại trên sàng với lưới cỡ 10,0 mm. Việc xử lý trong thử nghiệm đó sẽ làm cho các hạt bị nhỏ dần và kết quả thử nghiệm là tỷ lệ khối lượng hạt của lô thử lọt qua sàng đó ở cuối cuộc thử nghiệm. Một tỷ lệ cao trong thử nghiệm (vượt quá 10 % đến 25 %) chứng tỏ rằng tập hợp các chất đó có độ không hư hại thấp.
5.8.2. Các số liệu chỉ ra trong bảng 13 là các số liệu thu được trong một thí nghiệm, trong đó các cặp mẫu của tám tập hợp chất được gửi tới mười một phòng thí nghiệm và hai kết quả thử nghiệm về độ không bị hư hại bởi sunphat manhê thu được trên mỗi mẫu. Các mẫu có khối lượng xấp xỉ 100 kg (chúng được dùng cho một số lần thử nghiệm khác nhau) và các mẫu thử có khối lượng xấp xỉ 350 g.
5.8.3. Bảng 14, 15 và 16 chỉ ra phạm vi giữa các kết quả thử nghiệm, phạm vi giữa các mẫu và các trung bình ô được tính theo các công thức (21) đến (24) trong 5.4 2 chỉ đối với mức 6 của thí nghiệm.
Nếu sử dụng các phương trình (27) và (28) trong 5.5.3, phạm vi giữa các kết quả thử nghiệm trong bảng 14 và phạm vi giữa các mẫu trong bảng 15 sẽ cho:
![]()
Nếu áp dụng các phương trình (25) và (26) trong 5.4.2 đối với các trung bình ô trong bảng 16 ta được:
y6 = 19.0% (trung bình chung)
sr6 = 5.03%
như vậy nếu sử dụng các phương trình (29) đến (33) trong 5.5.5, các độ lệch chuẩn lặp lại và tái lập, và độ lệch chuẩn đo sự thay đổi giữa các mẫu sẽ bằng:
![]()
Bảng 17 đưa ra các kết quả tính toán cho các mức khác
5.8.4. Hình 4 chỉ rõ biểu đồ của các phạm vi giữa các kết quả thử nghiệm, các phạm vi giữa các mẫu, và các trung bình ô ở mức 6. Các đồ thị loại này đưa ra một bức tranh dễ hiểu về lượng biến đổi nẩy sinh từ các nguồn khác nhau (giữa các kết quả thử nghiệm, giữa các mẫu và giữa các phòng thí nghiệm). Hình 4 chỉ ra rằng, trong thí nghiệm này, ở mức 6 có sự thay đổi lớn giữa các trung bình ô mà nếu phương pháp thử nghiệm đó được sử dụng trong một quy định sẽ dẫn đến sự bất đồng do sự khác nhau giữa các kết quả của chúng giống như sự bất đồng giữa người bán và người mua, phạm vi giữa các mẫu nhỏ hơn phạm vi giữa các kết quả thử nghiệm, điều này gợi ý rằng sự biến đổi giữa các mẫu ở mức 6 là không đáng kể.
5.8.5. Giá trị của các thống kê h và k được tính như ở 5.6.1 cũng được chỉ ra trong bảng 14, 15 và 16 cho mức 6. Các giá trị đó cho tất cả các mức được vẽ thánh biểu đồ trong hình 5 đến 7. (Trong các hình đó các mức đã được sắp xếp lại theo thứ tự tăng dần của các trung bình chung như được chỉ ra trong bảng 17). Hình 5 chỉ ra rằng phòng thí nghiệm 6 đã thu được nhiều thống kê k với giá trị lớn đối với phạm vi giữa các kết quả thử nghiệm, điều này chứng tỏ rằng phòng thí nghiệm 6 có độ lặp lại xấu hơn so với các phòng thí nghiệm khác. Hình 6 chỉ ra rằng 3 phòng thí nghiệm (1, 6 và 10) thu được các thống kê k với các giá trị lớn đối với phạm vi giữa các mẫu: Điều này có lẽ là do các phòng thí nghiệm đó đã không tuân theo các thủ tục đã được khuyến cáo để chuẩn bị các mẫu thử từ các mẫu chung. Hình 7 chỉ ra rằng các thống kê h dương và âm trong hầu hết các phòng thí nghiệm (với các phòng thí nghiệm 1, 6,10, các thống kê đó có giá trị lớn nhất). Rõ ràng rằng có các độ chệch nhất quán theo hầu hết các phòng thí nghiệm, điều đó chứng tỏ rằng phương pháp thử nghiệm đó chưa được quy định một cách thích hợp.
5.8.6. Việc áp dụng các phép kiểm nghiệm Cochran và Grubb như trong 5.6.2 đối với các số liệu sẽ thu được các kết quả ở bảng 18. Hai giá trị bất thường được phát hiện. Do thiếu các thông tin khác, nên số liệu ứng với các giá trị bất thường đó cần phải được loại ra và cần phải tính lại. Sau đó cần tiếp tục việc phân tích với sự khảo sát mối quan hệ hàm số theo cách giống như với thiết kế đồng mức trong TCVN 6910-2 (ISO 5725-2).
|
|
|
|
|
Các trung bình ô |
Phạm vi giữa các mẫu |
Phạm vi giữa các kết quả thử nghiệm |
Hình 4 – Ví dụ 2 : Biểu đồ của các phạm vi và trung bình trích từ các bảng 14, 15 và 16 cho mức 6
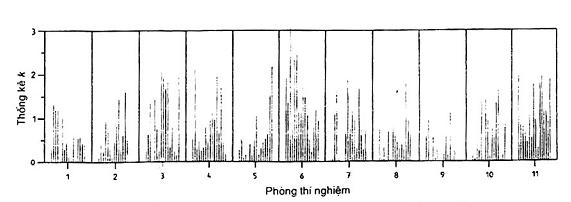
Hình 5 – Ví dụ 2: Kiểm tra sự phù hợp đối với phạm vi giữa các kết quả thử nghiệm
(được ghép nhóm theo phòng thí nghiệm)
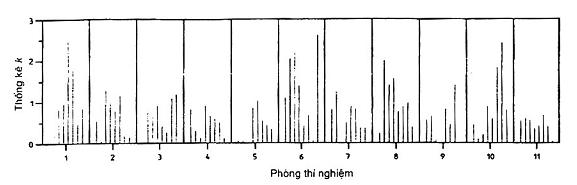
Hình 6 – Ví dụ 2: Kiểm tra sự phù hợp đối với các phạm vi giữa các mẫu
(được ghép nhóm theo phòng thí nghiệm)

Hình 7- Ví dụ 2: Kiểm tra sự phù hợp đối với các trung bình ô
(được ghép nhóm theo phòng thí nghiệm)
Bảng 13 – Ví dụ 2: Xác định sự không bị hư hại bởi sunphat manhê (%)
|
Phòng thí nghiệm |
Mẫu |
Mức1 |
Mức 2 |
Mức 3 |
Mức 4 |
|||||
|
Số kết quả thử nghiệm |
||||||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|||
|
1 |
1 |
69,2 |
67,0 |
7,4 |
8,0 |
4,1 |
3,5 |
10,4 |
10,1 |
|
|
2 |
69,7 |
71,7 |
6,6 |
5,7 |
10,5 |
13,1 |
13,9 |
13,8 |
||
|
2 |
1 |
66,5 |
64,1 |
1,9 |
2,1 |
3,0 |
3,2 |
8,7 |
6,7 |
|
|
2 |
65,7 |
65,8 |
4,2 |
3,3 |
1,9 |
1,1 |
8,3 |
4,8 |
||
|
3 |
1 |
68,7 |
69,5 |
6,3 |
5,8 |
2,4 |
2,9 |
11,7 |
7,0 |
|
|
2 |
67,7 |
77,7 |
9,7 |
5,3 |
2,1 |
3,3 |
7,9 |
12,0 |
||
|
4 |
1 |
77,5 |
75,3 |
2,0 |
3,6 |
2,4 |
1,4 |
9,4 |
7,1 |
|
|
2 |
76,3 |
77,2 |
4,7 |
3,8 |
6,4 |
2,3 |
10,7 |
7,7 |
||
|
5 |
1 |
55,4 |
63,2 |
3,8 |
4,1 |
1,3 |
0,8 |
3,7 |
6,3 |
|
|
2 |
65,9 |
54,7 |
2,1 |
3,1 |
0,7 |
1,7 |
3,3 |
3,7 |
||
|
6 |
1 |
64,8 |
70,9 |
8,4 |
6,1 |
6,0 |
9,7 |
16,5 |
12,3 |
|
|
2 |
78,2 |
73,4 |
8,3 |
10,6 |
12,4 |
9,8 |
13,2 |
16,8 |
||
|
7 |
1 |
64,8 |
63,4 |
4,3 |
5,7 |
2,9 |
3,0 |
7,5 |
9,3 |
|
|
2 |
67,0 |
63,4 |
7,7 |
3,9 |
4,3 |
6,4 |
11,1 |
8,3 |
||
|
8 |
1 |
64,9 |
68,4 |
4,4 |
2,8 |
1,3 |
2,8 |
5,7 |
6,8 |
|
|
2 |
65,4 |
65,5 |
5,4 |
6,7 |
2,7 |
2,8 |
4,8 |
5,5 |
||
|
9 |
1 |
– |
– |
– |
– |
1,1 |
0,0 |
6,6 |
7,0 |
|
|
2 |
– |
– |
– |
– |
0,7 |
3,7 |
4,9 |
6,3 |
||
|
10 |
1 |
57,0 |
57,7 |
3,3 |
0,4 |
2,1 |
2,4 |
5,5 |
5,8 |
|
|
2 |
57,1 |
52,7 |
4,2 |
2,3 |
3,6 |
3,5 |
3,9 |
5,7 |
||
|
11 |
1 |
70,6 |
75,2 |
5,3 |
6,4 |
5,7 |
1,9 |
9,5 |
7,2 |
|
|
2 |
77,9 |
68,2 |
3,5 |
7,1 |
1,4 |
3,0 |
8,1 |
7,4 |
||
|
Phòng thí nghiệm |
Mẫu |
Mức 5 |
Mức 6 |
Mức 7 |
Mức 8 |
|||||
|
Số kết quả thử nghiệm |
||||||||||
|
1 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|||
|
1 |
1 |
8,9 |
7,4 |
31,1 |
28,5 |
38,7 |
41,7 |
4,2 |
4,1 |
|
|
2 |
7,6 |
9,1 |
23,0 |
23,1 |
44,2 |
41,1 |
7,3 |
4,4 |
||
|
2 |
1 |
3,2 |
3,5 |
16,5 |
15,4 |
36,6 |
45,2 |
3,2 |
5,4 |
|
|
2 |
2,8 |
4,0 |
10,3 |
12,8 |
43,2 |
40,5 |
1,7 |
2,5 |
||
|
3 |
1 |
4,4 |
6,1 |
24,3 |
16,7 |
38,9 |
43,1 |
3,7 |
7,7 |
|
|
2 |
6,0 |
6,0 |
20,8 |
22,2 |
46,1 |
47,4 |
3,5 |
5,6 |
||
|
4 |
1 |
2,7 |
3,1 |
20,2 |
16,2 |
32,0 |
35,5 |
2,9 |
2,2 |
|
|
2 |
2,3 |
2,9 |
20,0 |
11,9 |
26,5 |
35,7 |
3,2 |
2,3 |
||
|
5 |
1 |
1,3 |
1,4 |
13,8 |
15,1 |
36,7 |
39,5 |
1,1 |
1,2 |
|
|
2 |
1,5 |
1,3 |
11,5 |
13,3 |
37,6 |
34,1 |
0,6 |
1,7 |
||
|
6 |
1 |
8,2 |
4,2 |
20,3 |
24,7 |
49,4 |
50,6 |
11,9 |
18,5 |
|
|
2 |
3,7 |
4,6 |
21,0 |
18,9 |
48,2 |
52,4 |
14,9 |
8,1 |
||
|
7 |
1 |
3,1 |
5,5 |
27,2 |
23,3 |
38,9 |
29,9 |
– |
1,7 |
|
|
2 |
5,6 |
5,5 |
21,5 |
22,7 |
34,4 |
38,3 |
2,2 |
5,0 |
||
|
8 |
1 |
1,8 |
2,2 |
13,6 |
12,0 |
27,0 |
37,0 |
0,3 |
2,2 |
|
|
2 |
4,0 |
4,0 |
15,6 |
16,7 |
39,7 |
34,6 |
3,6 |
3,7 |
||
|
9 |
1 |
3,8 |
3,8 |
17,7 |
17,1 |
33,4 |
33,1 |
1,8 |
2,0 |
|
|
2 |
3,5 |
2,8 |
21,4 |
16,8 |
26,5 |
25,2 |
2,5 |
1,6 |
||
|
10 |
1 |
3,5 |
3,0 |
21,7 |
23,9 |
35,3 |
26,5 |
0,5 |
4,3 |
|
|
2 |
3,2 |
3,5 |
27,0 |
32,5 |
18,0 |
18,2 |
2,0 |
2,1 |
||
|
11 |
1 |
3,5 |
2,5 |
11,0 |
18,4 |
27,0 |
33,5 |
5,1 |
3,9 |
|
|
2 |
2,0 |
2,8 |
16,4 |
8,1 |
35,4 |
29,3 |
2,1 |
5,0 |
||
Bảng 14 – Ví dụ 2: Phạm vi giữa các kết quả thử nghiệm cho mức 6
|
Phòng thí nghiệm |
Mẫu |
Phạm vi giữa các kết quả thử nghiệm % |
Thống kê k |
|
1 |
1 |
2,6 |
0,624 |
|
2 |
0,1 |
0,024 |
|
|
2 |
1 |
1,1 |
0,264 |
|
2 |
2,5 |
0,600 |
|
|
3 |
1 |
7,6 |
1,825 |
|
2 |
1,4 |
0,336 |
|
|
4 |
1 |
4,0 |
0,960 |
|
2 |
8,1 |
1,945 |
|
|
5 |
1 |
1,3 |
0,312 |
|
2 |
1,8 |
0,432 |
|
|
6 |
1 |
4,4 |
1,056 |
|
2 |
2,1 |
0,504 |
|
|
7 |
1 |
3,9 |
0,936 |
|
2 |
1,2 |
0,288 |
|
|
8 |
1 |
1,6 |
0,384 |
|
2 |
1,1 |
0,264 |
|
|
9 |
1 |
0,6 |
0,144 |
|
2 |
4,6 |
1,104 |
|
|
10 |
1 |
2,2 |
0,528 |
|
2 |
5,5 |
1,320 |
|
|
11 |
1 |
7,4 |
1,777 |
|
2 |
8,1 |
1,945 |
|
Bảng 15 – Ví dụ 2: Phạm vi giữa các mẫu cho mức 6 |
|
Bảng 16 – Ví dụ 2: Các trung bình ô cho mức 6 |
||||
|
Phòng thí nghiệm |
Phạm vi giữa các mẫu % |
Thống kê k |
|
Phòng thí nghiệm |
Trung bình ô % |
Thống kê h |
|
1 |
6,75 |
1,776 |
|
1 |
26,425 |
1,475 |
|
2 |
4,40 |
1,152 |
|
2 |
13,750 |
-1,043 |
|
3 |
1,00 |
0,262 |
|
3 |
21,000 |
0,397 |
|
4 |
2,25 |
0,589 |
|
4 |
17,075 |
-0,382 |
|
5 |
2,05 |
0,537 |
|
5 |
13,425 |
-1,108 |
|
6 |
2,55 |
0,668 |
|
6 |
21,225 |
0,442 |
|
7 |
3,15 |
0,825 |
|
7 |
23,675 |
0,929 |
|
8 |
3,35 |
0,877 |
|
6 |
14,475 |
-0,899 |
|
9 |
1,70 |
0,445 |
|
9 |
18,250 |
-0,149 |
|
10 |
6,95 |
1,819 |
|
10 |
26,275 |
1,445 |
|
11 |
2,55 |
0,668 |
|
11 |
13,425 |
1,108 |
Bảng 17 – Ví dụ 2: Các giá trị của các trung bình, tổng bình phương của các phạm vi, và độ lệch chuẩn được tính từ các số liệu cho tất cả 8 mức trong bảng 13
(loại ra các ô vài các số liệu bị thiếu)
|
Mức j |
Số các phòng thí nghiệm p |
Trung bình chung yj% |
Tổng bình phương các phạm vi |
Các độ lệch chuẩn |
||||
|
SSrj(%)2 |
SSHJ(%)2 |
syj% |
srj% |
sRj% |
sHj% |
|||
|
3 |
11 |
3,7 |
82,99 |
96,3725 |
2,62 |
1,37 |
2,56 |
1,85 |
|
5 |
11 |
4,0 |
34,70 |
11,2550 |
1,88 |
0,89 |
2,01 |
0,34 |
|
8 |
10 |
4,1 |
155,39 |
29,4225 |
3,49 |
1,97 |
3,92 |
0,00 |
|
2 |
10 |
5,0 |
83,51 |
25,2375 |
1,95 |
1,44 |
2,29 |
0,47 |
|
4 |
11 |
8,2 |
131,07 |
23,5775 |
3,10 |
1,73 |
3,47 |
0,00 |
|
6 |
11 |
19,0 |
381,66 |
160,5300 |
5,03 |
2,95 |
5,51 |
1,72 |
|
7 |
11 |
36,5 |
636,19 |
305,4775 |
7,28 |
3,80 |
7,78 |
2,58 |
|
1 |
10 |
67,4 |
529,71 |
92,9225 |
6,23 |
3,64 |
7,05 |
0,00 |
Bảng 18 – Ví dụ 2: Các giá trị của thống kê Grubb và Cochran
|
Mức j |
Số các phòng thí nghiệm p |
Thống kê Cochran cho các phạm vi giữa các kết quả thử nghiệm |
Thống kê Cochran cho các phạm vi giữa các mẫu |
|||||||
|
3 |
11 |
0,203 |
0,664 * (1) |
|||||||
|
5 |
11 |
0,461 ** (6) |
0,374 |
|||||||
|
8 |
10 |
0,298 |
0,465 |
|||||||
|
2 |
10 |
0,232 |
0,238 |
|||||||
|
4 |
11 |
0,169 |
0,550 |
|||||||
|
6 |
11 |
0,172 |
0,301 |
|||||||
|
7 |
11 |
0,157 |
0,536 |
|||||||
|
1 |
10 |
0,237 |
0,680 * (6) |
|||||||
|
Các thống kê Grubb cho các trung bình ô |
||||||||||
|
Mức j |
Số các phòng thí nghiệm p |
Một giá trị nhỏ nhất |
Hai giá trị nhỏ nhất |
Hai giá trị lớn nhất |
Một giá trị lớn nhất |
|||||
|
3 |
11 |
0,970 |
0,791 |
0,098** (1;6) |
2,219 |
|||||
|
5 |
11 |
1,396 |
0,709 |
0,302 |
2,266 |
|||||
|
8 |
10 |
0,849 |
– |
– |
2,643**(6) |
|||||
|
2 |
10 |
1,259 |
0,614 |
0,466 |
1,713 |
|||||
|
4 |
11 |
1,290 |
0,681 |
0,294 |
2,082 |
|||||
|
6 |
11 |
1,108 |
0,700 |
0,479 |
1,475 |
|||||
|
7 |
11 |
1,649 |
0,562 |
0,453 |
1,875 |
|||||
|
1 |
10 |
1,808 |
0,345 |
0,590 |
1,476 |
|||||
|
Chú thích – Các số trong ngoặc biểu thị các phòng thí nghiệm đưa ra các giá trị tản mạn tiêu chuẩn là như sau: |
||||||||||
|
Phép thử nghiệm thống kê |
Áp dụng cho |
Số các phòng thí nghiệm |
Chỉ số trong bảng TCVN 6910-2 (ISO 5725-2) |
Giá trị tản mạn |
Giá trị bất thường |
|||||
|
|
|
p’ |
p |
(*) |
(**) |
|||||
|
Phép kiểm nghiệm Cochran |
Phạm vi giữa các kết quả thử nghiệm |
10 11 |
20 20 |
0,389 0,365 |
0,480 0,450 |
|||||
|
Phép kiểm nghiệm Cochran |
Phạm vi giữa các mẫu |
10 11 |
10 11 |
0,602 0,570 |
0,718 0,684 |
|||||
|
Phép kiểm nghiệm Grubb cho một giá trị bất thường |
Trung bình ô |
10 11 |
10 11 |
2,290 2,355 |
2,482 2,564 |
|||||
|
Phép kiểm nghiệm Grubb cho cặp giá trị bất thường |
Trung bình ô |
10 11 |
10 11 |
0,186 4 0,2213 |
0,1150 0,1448 |
|||||
5.9. Các công thức tổng quát để tính toán với thiết kế cho vật liệu không đồng nhất
Tính các thống kê sau đây ở mỗi mức j:
a) Trung bình chung (với tổng lấy theo i, t, k)
![]()
trong đó nj là số các kết quả thử nghiệm bao gồm trong tổng
b) Các hiệu quả phòng thí nghiệm với mỗi i (với tổng lấy theo t và k):
![]()
= trung bình phòng thí nghiệm – trung bình chung.
trong đó nij là số các kết quả thử nghiệm bao gồm trong tổng:
c) Các hiệu quả mẫu với mỗi i và t (với tổng lấy theo k):
![]()
= trung bình mẫu – trung bình phòng thí nghiệm.
trong đó nijt là số các kết quả thử nghiệm bao gồm trong tổng.
d) Các phần dư đối với i, t, k:
![]()
= kết quả thử nghiệm – trung bình mẫu.
e) Tổng bình phương đối với các mẫu (với tổng lấy theo i):
![]()
f) Tổng bình phương đối với các mẫu (với tổng lấy theo i, t):
![]()
g) Tổng bình phương đối với sự lặp lại (với tổng lấy theo i, t và k):
![]()
h) Các bậc tự do:
![]()
trong đó
p’j là số phòng thí nghiệm có báo cáo ít nhất một kết quả thử nghiệm.
gi là số các mẫu có ít nhất một kết quả thử nghiệm được báo cáo.
n là tổng số các kết quả thử nghiệm.
i) Các thừa số đối với mỗi i (với tổng lấy theo t):

j) Các thừa số (với tổng lấy theo i):

k) Độ lệch chuẩn lặp lại sr, độ lệch chuẩn giữa các mẫu sHj, độ lệch chuẩn giữa các phòng thí nghiệm sLj và độ lệch chuẩn tái lập sRJ (khi sử dụng ) được cho bởi:
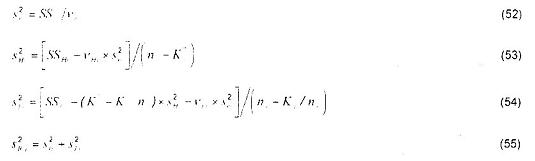
Chú thích – Các công thức trên được dẫn ra bằng cách sử dụng lý thuyết thống kê của Scheffé [4]
5.10 Ví dụ 3: Áp dụng các công thức tổng quát
5.10.1. Các số liệu của ví dụ 2, mức 4, được sử dụng để làm ví dụ áp dụng các công thức tổng quát bằng cách bỏ qua một số các kết quả thử nghiệm (xem bảng 19). Công thức trong 5.9 cho trung bình chung tính theo công thức được cho ở 5.9 phía dưới bảng 19; tổng các bình phương, các bậc tự do, các thừa số được chỉ ra ở phía dưới bảng 20, 21 và 22.
5.10.2. Khi áp dụng các phương trình (52) -(55) ở bước k của 5.9 ta thu được:
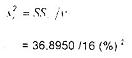
vậy
![]()
và

như vậy
![]()
và

như vậy
![]()
và

Bảng 19 – Ví dụ 3: Xác định độ không bị hư hại bởi sunphát manhê ở mức 4
|
Phòng thí nghiệm i |
Mẫu t |
Kết quả thử nghiệm k = 1 % |
Kết quả thử nghiệm k = 2 % |
|
1 |
1 |
– |
10,1 |
|
2 |
13,9 |
13,8 |
|
|
2 |
1 |
– |
– |
|
2 |
8,3 |
4,8 |
|
|
3 |
1 |
– |
7,0 |
|
2 |
– |
12,0 |
|
|
4 |
1 |
9,4 |
– |
|
2 |
– |
– |
|
|
5 |
1 |
3,7 |
6,3 |
|
2 |
3,3 |
3,7 |
|
|
6 |
1 |
16,5 |
12,3 |
|
2 |
13,2 |
16,8 |
|
|
7 |
1 |
7,5 |
9,3 |
|
2 |
11,1 |
8,3 |
|
|
8 |
1 |
5,7 |
6,8 |
|
2 |
4,8 |
5,5 |
|
|
9 |
1 |
6,6 |
7,0 |
|
2 |
4,9 |
6,3 |
|
|
10 |
1 |
5,5 |
5,8 |
|
2 |
3,9 |
5,7 |
|
|
11 |
1 |
9,5 |
7,2 |
|
2 |
8,1 |
7,4 |
|
|
Trung bình chung |
mj= 8,1111 % |
|
|
|
Số các kết quả thử nghiệm |
nj = 36 |
|
|
Bảng 20 – Ví dụ 3: Tính tổng các bình phương cho các phòng thí nghiệm
|
Phòng thí nghiệm i |
Trung bình, phòng thí nghiệm % |
Số các kết quả thử nghiệm nij |
Hiệu quả phòng thí nghiệm Bij % |
Thừa số Kij |
|
1 |
12,600 |
3 |
4,488 9 |
5 |
|
2 |
6,550 |
2 |
– 1,561 1 |
4 |
|
3 |
9,500 |
2 |
1,388 9 |
2 |
|
4 |
9,400 |
1 |
1,288 9 |
1 |
|
5 |
4,250 |
4 |
– 3,861 1 |
8 |
|
6 |
14,700 |
4 |
– 6,588 9 |
8 |
|
7 |
9,050 |
4 |
0,938 9 |
8 |
|
8 |
5,700 |
4 |
– 2,411 1 |
8 |
|
9 |
6,200 |
4 |
– 1,911 1 |
8 |
|
10 |
5,225 |
4 |
– 2,886 1 |
8 |
|
11 |
8,050 |
4 |
– 0,061 1 |
8 |
|
Tổng bình phương cho các phòng thí nghiệm |
SSLj = 378,853 1 (%)2, |
|||
|
Bậc to do cho các phòng thí nghiệm, |
yLj = 11 – 1 = 10 |
|||
|
Các thừa số |
Kj = 130 K’j = 68 K”j = 19,667 |
|||
Bảng 21 – Ví dụ 3: Tính tổng bình phương cho các mẫu
|
Phòng thí nghiệm i |
Mẫu t |
Trung bình mẫu % |
Số các kết quả thử nghiệm nijt |
Hiệu quả mẫu Hijt % |
|
1 |
1 |
10,10 |
1 |
– 2,500 |
|
2 |
13,85 |
2 |
1,250 |
|
|
2 |
1 |
– |
0 |
– |
|
2 |
6,55 |
2 |
0,000 |
|
|
3 |
1 |
7,00 |
1 |
– 2,500 |
|
2 |
12,00 |
1 |
2,500 |
|
|
4 |
1 |
9,40 |
1 |
0,000 |
|
2 |
– |
0 |
– |
|
|
5 |
1 |
5,00 |
2 |
0,750 |
|
2 |
3,50 |
2 |
– 0,750 |
|
|
6 |
1 |
14,40 |
2 |
– 0,300 |
|
2 |
15,00 |
2 |
0,300 |
|
|
7 |
1 |
8,40 |
2 |
– 0,650 |
|
2 |
9,70 |
2 |
0,650 |
|
|
8 |
1 |
6,25 |
2 |
0,550 |
|
2 |
5,15 |
2 |
– 0,550 |
|
|
9 |
1 |
6,80 |
2 |
0,600 |
|
2 |
5,60 |
2 |
– 0,600 |
|
|
10 |
1 |
5,65 |
2 |
0,425 |
|
2 |
4,80 |
2 |
-0,425 |
|
|
11 |
1 |
8,35 |
2 |
0,300 |
|
2 |
7,55 |
2 |
– 0,300 |
|
|
Tổng bình phương cho các mẫu |
SSHJ= 29,907 5 (%)2, |
|
||
|
Bậc tự do cho các mẫu |
VHJ = 20 – 11 = 9 |
|
|
|
Bảng 22 – Ví dụ 3: Tính tổng bình phương cho độ lặp lại
|
Phòng thí nghiệm i |
Mẫu t |
Kết quả thử nghiệm k = 1 % |
Kết quả thử nghiệm k = 2 % |
|
1 |
1 |
– |
0,00 |
|
2 |
0,05 |
-0.05 |
|
|
2 |
1 |
– |
– |
|
2 |
1,75 |
1,75 |
|
|
3 |
1 |
– |
0,00 |
|
2 |
– |
0,00 |
|
|
4 |
1 |
0,00 |
– |
|
2 |
– |
– |
|
|
5 |
1 |
-1,30 |
1,30 |
|
2 |
-0,20 |
0,20 |
|
|
6 |
1 |
2,10 |
-2,10 |
|
2 |
-1,80 |
1,80 |
|
|
7 |
1 |
-0,90 |
0,90 |
|
2 |
1,40 |
-1,40 |
|
|
8 |
1 |
-0,55 |
0,55 |
|
2 |
-0,35 |
0,35 |
|
|
9 |
1 |
-0,20 |
0,20 |
|
2 |
-0,70 |
0,70 |
|
|
10 |
1 |
-0,15 |
0,15 |
|
2 |
-0,90 |
0,90 |
|
|
11 |
1 |
1,15 |
-1,15 |
|
2 |
0,35 |
-0,35 |
|
|
Tổng bình phương cho độ lặp lại |
SSrj = 36,895 (%)2. |
|
|
|
Bậc tự do cho độ lặp lại |
vrj = 36 – 20 = 16 |
|
|
6. Phương pháp ổn định để phân tích số liệu
6.1. Áp dụng các phương pháp ổn định để phân tích số liệu
6.1.1. TCVN 6910-2 (ISO 5725-2), khuyến nghị cần áp dụng hai phép kiểm nghiệm (Cochran và Grubb) về giá trị bất thường đối với các số liệu thu được trong thí nghiệm về độ chụm. Bất kỳ số liệu nào tạo ra một thống kê kiểm nghiệm trong hai phép kiểm nghiệm trên có giá trị vượt quá giá trị tới hạn ở mức ý nghĩa 1 % cần phải được loại bỏ (trừ khi nhà thống kê có lý do xác đáng để giữ lại số liệu đó). Trên thực tế thường không dễ áp dụng cách này. Xét kết quả của các phép kiểm nghiệm giá trị bất thường trong ví dụ 1 của 4.8. Các kết quả đó được đưa ra trong bảng 8. Phòng thí nghiệm 5 đưa ra một trung bình ở vượt trội duy nhất (ở mức 10) và nó cần được phân loại là giá trị bất thường, theo phép kiểm nghiệm Grubb, nhưng nó đưa ra ba giá trị tản mạn khác và thể hiện rõ trong hình 3 rằng có điều gì đó sai sót trong phòng thí nghiệm này. Trong tình huống này nhà thống kê cần phải quyết định lựa chọn giữa:
a) giữ lại tất cả số liệu của phòng thí nghiệm 5
b) loại bỏ chỉ một số liệu ở mức 10 của phòng thí nghiệm 5.
c) loại bỏ tất cả các số liệu của phòng thí nghiệm 5.
Quyết định này sẽ ảnh hưởng thực sự đến các giá trị tính được cho độ lệch chuẩn lặp lại và tái lập. Theo kinh nghiệm chung, khi phân tích số liệu từ các thí nghiệm về độ chụm để phát hiện các số liệu nằm trên biên giới giữa các giá trị tản mạn và bất thường, cần có các phán quyết và điều này ảnh hưởng đến kết quả tính toán. Nhưng điều đó có thể không thỏa đáng. Các phương pháp ổn định được mô tả trong điều này cho phép phân tích các số liệu theo cách sao cho không đòi hỏi thực hiện các quyết định có ảnh hưởng đến kết quả tính toán. Như vậy nếu có lý do để cho rằng các kết quả của thí nghiệm về độ chụm sẽ chứa các số liệu bất thường, phương pháp ổn định có thể được ưa chuộng hơn.
6.1.2. Mô hình cơ bản trình bày trong điều 5 của TCVN 6910-1: 2001 (ISO 5725-1:1994) dựa trên giả thiết rằng đã thiết lập được đúng đắn một giá trị chung cho độ lệch chuẩn lặp lại và tái lập đối với tất cả các phòng thí nghiệm sử dụng phương pháp đo đó. Trong thực tế thường thấy một số phòng thí nghiệm có độ lặp lại xấu hơn các phòng thí nghiệm khác. Ví dụ, hãy xem hình 5 của ví dụ 2 trong 5.8, phòng thí nghiệm 6 rõ ràng có độ lặp lại xấu hơn nhiều so với phòng thí nghiệm 9 trong thí nghiệm đó. Như vậy giả thiết các phòng thí nghiệm đạt được độ lặp lại tương tự tỏ ra không còn đúng trong trường hợp này. Một số người tham gia trong thí nghiệm về độ chụm có thể đạt độ lặp lại xấu trong thời gian đầu, khi một phương pháp đo được quy định cho một thí nghiệm về độ chụm hoặc khi họ có ít kinh nghiệm về phương pháp đo đó, và trong các tình huống đó việc sử dụng phương pháp ổn định sẽ đặc biệt thích hợp.
6.1.3. Mục đích của việc sử dụng phương pháp ổn định khi phân tích số liệu của một thí nghiệm độ chụm là tính các giá trị của độ lệch chuẩn lặp lại và tái lập theo một cách sao cho chúng không bị ảnh hưởng bởi các số liệu bất thường. Nếu những người tham gia thí nghiệm đó coi như được phân thành hai nhóm, một nhóm tạo ra các số liệu với chất lượng tốt, nhóm kia tạo ra các số liệu với chất lượng xấu, khi đó phương pháp ổn định sẽ tạo ra các các giá trị của độ lệch chuẩn lặp lại và tái lập phù hợp với lớp số liệu có chất lượng tốt và không bị ảnh hưởng bởi các số liệu có chất lượng xấu (nếu như lớp các số liệu có chất lượng xấu không quá lớn).
6.1.4. Việc sử dụng phương pháp ổn định để phân tích số liệu không ảnh hưởng đến việc lập kế hoạch, tổ chức hoặc thực thi thí nghiệm về độ chụm. Việc quyết định nên sử dụng phương pháp ổn định hay phương pháp đòi hỏi phải loại bỏ các số liệu bất thường cần được tiến hành bởi các chuyên gia thống kê và phải báo cáo lên hội đồng chuyên môn. Khi sử dụng phương pháp ổn định cần phải áp dụng các phép kiểm nghiệm giá trị bất thường và kiểm tra sự phù hợp được mô tả trong TCVN 6910-2 (ISO 5725-2) hoặc TCVN 6910 – 5 cho các số liệu và các nguyên nhân của giá trị bất thường hoặc các kiểu dáng của các thống kê h và k cần phải được nghiên cứu. Tuy nhiên không cần phải loại bỏ các số liệu do các kết quả của việc kiểm nghiệm và kiểm tra.
6.1.5. Theo phương pháp tính toán các thống kê h, k mô tả trong TCVN 6910-2 (ISO 5725-2) mẫu số trong các thống kê đó là độ lệch chuẩn được tính từ các số liệu đã được báo cáo. Nếu có số liệu bất thường trong các số liệu đó thì chúng sẽ làm cho mẫu số lớn lên và tạo ra sai lệch trong đồ thị của các thống kê đó. Ví dụ, nếu ở một mức của thí nghiệm, một phòng thí nghiệm nào đó đưa ra giá trị trung bình ô bất thường vượt trội hẳn so với các giá trị bất thường khác ở cùng mức đó thì đồ thị của thống kê h sẽ biểu hiện một giá trị h lớn khác thường. Tuy nhiên các thống kê h đối với tất cả các phòng thí nghiệm khác ở mức đó sẽ là nhỏ, thậm chí một số trong các phòng thí nghiệm đã đưa ra các giá trị bất thường. Việc sử dụng trung bình chung để tính thống kê h có thể dẫn tới một hiệu quả tương tự. Việc sử dụng các ước lượng ổn định của độ lệch chuẩn cho các mẫu số trong thống kê h và k và việc sử dụng ước lượng ổn định của các giá trị trung bình chung để tính các thống kê h sẽ tránh được sai lệch đó. Vì vậy nên dùng các ước lượng đó cho mục đích này.
6.1.6. Các số liệu của thí nghiệm độ chụm cho phép tính hai loại thống kê.
a) các trung bình ô, từ đó độ lệch chuẩn có thể tính được, độ lệch chuẩn này là thước đo sự biến đổi giữa các phòng thí nghiệm.
b) các độ lệch chuẩn hoặc các phạm vi (hoặc độ sai khác trong thiết kế mức tách biệt) trong các ô và chúng được kết hợp lại để cho một thước đo về sự biến đổi trong các phòng thí nghiệm.
Phương pháp ổn định nêu ra ở đây không thay thế các trung bình ô, các độ lệch chuẩn, các phạm vi hoặc độ sai khác, nhưng nó đưa ra các cách kết hợp khác các đại lượng đó để thu được một thống kê dùng để tính độ lệch chuẩn lặp lại và tái lập.
Ví dụ, với các số liệu ở một mức của thiết kế đồng mức đã được trình bày trong TCVN 6910-2 (ISO 5725-2), giai đoạn đầu tiên của việc phân tích là tính giá trị trung bình, độ lệch chuẩn của các kết quả đo trong mỗi ô. Sau đó sử dụng trung bình ô để tính độ lệch chuẩn, dùng làm thước đo sự biến đổi giữa các phòng thí nghiệm. Khi phương pháp ổn định của điều này được sử dụng, việc tính toán này được thực hiện theo “thuật toán A” và các trung bình ô không bị loại ra khi tính toán dù cho kết quả của việc áp dụng phép kiểm nghiệm Grubb là như thế nào. Cũng như vậy trong thiết kế này, các độ lệch chuẩn ô được kết hợp lại với nhau để đưa ra một ước lượng của độ lệch chuẩn lặp lại. Với việc phân tích ổn định, điều đó được thực hiện theo “thuật toán S” và các độ lệch chuẩn ô không bị loại ra khi áp dụng phép kiểm nghiệm Cochran. Với mỗi cách tiếp cận (được mô tả trong TCVN 6910-2 (ISO 5725-2) hoặc ở đây) hai thước đo đó được sử dụng để tính ước lượng của độ lệch chuẩn lặp lại và tái lập theo cùng một cách.
Một ví dụ phức tạp hơn là thiết kế xếp chồng so le 6 yếu tố được nêu trong phụ lục C của TCVN 6910 – 3: 2001. Với thiết kế này giai đoạn đầu tiên của việc phân tích là tính giá trị trung bình của các số liệu cho mỗi phòng thí nghiệm (ở mỗi mức) và chúng được ký hiệu bởi yi(1),….. yi(5), và dẫy các phạm vi được ký hiệu bởi wi(1),…..wi(5), chúng chứa các thông tin về sự biến đổi gắn với các yếu tố khác nhau được kiểm tra trong thí nghiệm. Để phân tích các số liệu khi sử dụng phương pháp ổn định được trình bày ở đây, “thuật toán A” được áp dụng các các trung bình ô và “thuật toán S” được áp dụng cho dẫy các phạm vi. Sử dụng các thống kê thu được bởi các thao tác đó được sử dụng để thu được các ước lượng của độ chụm lặp lại, độ chụm trung gian và độ lệch chuẩn tái lập, theo cùng một cách như khi áp dụng phương pháp phân tích được nêu trong TCVN 6910 – 3.
6.1.7. Các phương pháp ổn định được chọn trong tiêu chuẩn này vì chúng có thể áp dụng cho tất cả các thiết kế thí nghiệm được nêu ra trong các phần 2, 3, 4 và 5 của TCVN 6910 và vì việc tính toán tương đối đơn giản. Tuy nhiên cần lưu ý rằng các phương pháp này đưa ra những cách kết hợp một cách ổn định các trung bình ô, độ lệch tiêu chuẩn ở và các phạm vi ô. Chúng không kết hợp các kết quả thử nghiệm đơn lẻ theo cách ổn định, tức là chúng bắt đầu với các trung bình số học của các trung bình ô và của các độ lệch chuẩn ô. Có những phương pháp ổn định kết hợp các kết quả thử nghiệm trong các ô theo cách ổn định và việc áp dụng chúng trở nên phức tạp hơn trong thực hành.
6.2. Phân tích ổn định: Thuật toán A
6.2.1. Thuật toán này tạo ra các giá trị ổn định của giá trị trung bình và độ lệch chuẩn của các số liệu được dùng và nó được áp dụng cho:
a) các trung bình ô, theo một thiết kế bất kỳ;
b) độ sai khác ô, theo thiết kế mức tách biệt.
6.2.2. Ký hiệu p thành phần của số liệu được sắp xếp theo thứ tự tăng bởi:
x1, x2,……, xi,……, xp
Ký hiệu trung bình và độ lệch chuẩn ổn định của các số liệu này bởi x* và s*.
6.2.3. Tính các giá trị ban đầu của x* và s* như sau:
x* = trung vị của của các xi(i = 1, 2,…, p) (56)
s*= 1,483 x trung vị của các |x1 – x*|, (i = 1, 2,…, p) (57)
6.2.4. Cập nhật các giá trị của x* và s* như sau:
Tính
j = 1,5s* (58)
với mỗi giá trị x1(i = 1, 2,…, p), tính:

Tính các giá trị mới của x* và s* từ:

6.2.5. Các ước lượng ổn định x* và s* có thể được dẫn ra bằng cách tính lặp, tức là bằng cách lặp lại việc tính toán trong 6.2.4 nhiều lần, cho đến khi sự biến đổi của các ước lượng của x* và s* giữa hai lần tính liên tiếp là nhỏ. Đó là một phương pháp đơn giản cho việc lập trình trên máy vi tính.
6.2.6. Một phương pháp khác không cần tính lặp và như vậy rất tiện dụng khi tính toán bằng tay, được đưa ra bởi nhận xét rằng các phương trình (60) và (61) trong 6.2.4 có thể viết dưới dạng:

trong đó
uL là số các thành phần xi của số liệu mà xi < x* – j
uU là số các thành phần xi của số liệu mà xi > x* + j
x’ và s’ là trung bình và độ lệch chuẩn của (p – uL – uU) các thành phần xi của số liệu đối với nó |xi – x*| ≤ j
Các đại lượng này được dùng để tính x* và s* một cách trực tiếp nếu uL và uU đã biết. Một cách tiếp cận nữa là hãy thử các khả năng khác nhau theo một thứ tự có hệ thống (tức là hãy thử uL = 0, uU = 0; tiếp đó uL = 0, uU = 1; uL = 1, uU = 0; uL = 1, uU = 1 và tiếp tục) cho đến khi tìm được một lời giải hợp lý trong đó số lượng thực sự của các thành phần của số liệu mà chúng sai khác với x* một lượng lớn hơn 1,5s* bằng các giá trị uL và uU được dùng để tính x* và s*. Trong thực tế, người phân tích có thể sử dụng các biểu đồ trong hình 4 để nhận ra các giá trị tỏ ra khác với x* một lượng lớn hơn 1,5s* và như vậy sẽ tìm được lời giải bằng cách đánh giá với một số ít các trường hợp.
Một khả năng nữa là sử dụng phương pháp lặp để tìm lời giải xấp xỉ, sau đó giải các phương trình (62) và (63) để tìm lời giải chính xác. Đó là một cách tiếp cận được sử dụng trong ví dụ dưới đây.
6.3. Phân tích ổn định: Thuật toán S
6.3.1. Thuật toán này được áp dụng cho các độ lệch chuẩn trong phòng thí nghiệm (hoặc các phạm vi trong phòng thí nghiệm) trong một thiết kế bất kỳ. Nó tạo ra một giá trị kết hợp ổn định của các độ lệch chuẩn và các phạm vi mà thuật toán áp dụng với chúng.
6.3.2. Ký hiệu p thành phần của dữ liệu được sắp xếp theo thứ tự tăng dần bởi:
w1, w2 …… wp….. wp’
(Các đại lượng này có thể là phạm vi hoặc độ lệch chuẩn).
Ký hiệu giá trị kết hợp ổn định bởi w* và bậc tự do ứng với mỗi wi, bởi v. (Khi wi là phạm vi, v = 1. Khi wi là độ lệch chuẩn của n kết quả, v = n -1). Các giá trị x và h cần thiết cho thuật toán này được cho trong bảng 23.
6.3.3. Tính giá trị ban đầu cho w* như sau:
w* = trung vị của các wi(i = 1,2,…, p) (64)
6.3.4. Cập nhật giá trị của w* như sau
Tính
Y = h x w* (65)
với mỗi giá trị wi(i = 1,2,…, p), tính:

Tính giá trị mới của w* từ:

6.3.5. Ước lượng ổn định w* có thể được dẫn ra bảng cách tính lặp lại các tính toán trong 6.3.4 nhiều lần cho đến khi sự biến đổi theo ước lượng của w* giữa hai lần tính toán liên tiếp là nhỏ. Đó là một phương pháp đơn giản cho việc lập trình trên máy tính.
6.3.6. Một phương pháp khác không cần tính lặp và như vậy rất tiện dụng khi tính toán bằng tay, tương tự với phương pháp đã nêu trong 6.2.6. Phương trình (67) trong 6.3.4 có thể được viết dưới dạng:

trong đó
S’ là tổng lấy theo các wi sao cho wi ≤ Y
uU là số các wi sao cho wi > Y
Điều này có thể giải quyết bằng cách thử uU = 0, uU =1, uU = 2, v.v… cho đến khi có được một lời giải hợp lý, trong đó số lượng thực sự các wi vượt quá h x w* bằng uU. Trong thực tế, nhà phân tích sẽ có thể sử dụng biểu đồ trong hình 4 để nhận ra các phạm vi tỏ ra vượt h x w* và tìm được lời giải bảng cách đánh giá với một số ít trường hợp.
Cách tiếp cận dùng trong ví dụ sau là sử dụng phương pháp lặp để tìm một lời giải xấp xỉ, sau đó giải phương trình (68) để tìm lời giải chính xác.
Bảng 23 – Các yếu tố cần thiết cho phân tích ổn định: Thuật toán S
|
Bậc tự do y |
Thừa số giới hạn h |
Thừa số hiệu chỉnh x |
|
1 |
1,645 |
1,097 |
|
2 |
1,517 |
1,054 |
|
3 |
1,444 |
0,039 |
|
4 |
1,395 |
1,032 |
|
5 |
1,359 |
1,027 |
|
6 |
1,332 |
1,024 |
|
7 |
1,310 |
1,021 |
|
8 |
1,292 |
1,019 |
|
9 |
1,277 |
10,18 |
|
10 |
1.264 |
1,017 |
|
Chú thích: Giá trị của x và h được dẫn ra theo phụ lục B |
||
6.4. Các công thức: Phân tích ổn định ở một mức cụ thể của thiết kế đồng mức
6.4.1. Với thiết kế đồng mức, một ước lượng của độ lệch chuẩn lặp lại sr ở một mức có thể thu được bằng cách áp dụng thuật toán S đối với các phạm vi ở hoặc các độ lệch tiêu chuẩn ô đề tính giá trị ổn định của w từ phương trình (67) trong 6.3.4. Nếu thuật toán S được áp dụng đối với các độ lệch chuẩn ô thì
sr = w* (69)
Nếu có hai kết quả đo trên một ô và thuật toán S được áp dụng cho các phạm vi ô, thì
(70)
6.4.2. Ước lượng ổn định của độ lệch chuẩn của các trung bình ô sd cho một mức có thể thu được bằng cách áp dụng thuật toán A đối với các trung bình ô cho mức đó để thu được một giá trị ổn định s* từ phương trình (61) trong 6.2.4 và sau đó sử dụng
sd = s (71)
6.4.3. Tiếp theo độ lệch chuẩn giữa phòng thí nghiệm sL có thể được dẫn ra khi sử dụng

trong đó n là số các kết quả đo ở mỗi ô.
Nếu biểu thức dưới dấu căn bậc hai là âm thì đặt
sD = 0 (73)
Tính độ lệch chuẩn tái lập ở mức đó
![]()
6.5. Ví dụ 4: Phân tích ổn định ở một mức cụ thể của thiết kế đồng mức
6.5.1. Ví dụ 3 trong TCVN 6910-2:2001 (ISO 5725-2:1994) là một ví dụ của thiết kế đồng mức trong đó số liệu chứa các giá trị tản mạn và bất thường. Mức 5 trong ví dụ đó là một mức đáng lưu ý vì phòng thí nghiệm 1 đưa ra một trung bình ô tỏ ra là gần tản mạn theo phép kiểm nghiệm Grubb và phòng thí nghiệm 6 đưa ra một trung bình ô tỏ ra là gần tản mạn theo phép kiểm nghiệm Cochran. Các số liệu đó được tái tạo lại ở đây trong bảng 24.
6.5.2. Nếu số liệu từ tất cả các phòng thí nghiệm đều được giữ lại, các độ lệch chuẩn lặp lại và tái lập có thể được ước lượng bằng cách sử dụng các công thức trong 7.4 của TCVN 6910-2:2001 (ISO 5725- 2:1994) và cho ta
p = 9
m = 20,511
sr = 0,585
sd = 1,727
sL = 1,677
sR = 1,776
6.5.3. Tuy nhiên, theo TCVN 6910-2 (ISO 5725-2): nhà phân tích số liệu đã sử dụng thông tin từ các mức khác trong thí nghiệm và các nghi ngờ liên quan tới việc nhận dạng các mẫu được thử nghiệm bởi phòng thí nghiệm 6 để lý giải việc loại bỏ các số liệu của cả hai phòng thí nghiệm 1 và 6 khi tính toán và tính được
p = 7
m = 20,412
sr = 0,393
sd = 0,573
sL = 0,501
sR = 0,637
Rõ ràng rằng việc quyết định loại các số liệu từ hai phòng thí nghiệm đó đã có ảnh hưởng thực sự đến các ước lượng của độ Iêch chuẩn lặp lại và tái lập.
6.5.4. Bước đầu tiên trong việc phân tích là thu được một ước lượng ổn định của độ lệch chuẩn lặp lại. Việc tính toán có thể được thực hiện một cách tiện lợi như được chỉ ra trong bảng 25, trong đó các phạm vi ô đã được sắp xếp theo thứ tự tăng. Việc sử dụng thuật toán S và bằng cách lặp lại đưa đến các kết quả được chỉ ra trong bảng 25. Trong ví dụ này bậc tự do của mỗi phạm vi ô là v = 1, như vậy x = 1,097 và h =1,645. Sau bốn bước lặp được chỉ ra trong bảng, giá trị ổn định thu được w* » 0,7 và chỉ có một phạm vi ô (w9 = 1,98) vượt quá y. Nếu các tính toán được thực hiện trên máy tính, quá trình này có thể được tiếp tục cho đến khi sự biến đổi theo giá trị của w* giữa hai lần lặp liên tiếp là nhỏ.
Lời giải cũng có thể được dẫn ra một cách trực tiếp như sau: việc sử dụng phương trình (68) trong 6.3.6 với
uU = 1
![]()
cho
![]()
và đưa đến lời giải (nếu giả thiết uU = 1 là đúng)
w* = 0,69 % dấu criôsốt (dầu lấy từ cây giẻ gai)
Có thể khẳng định rằng giá trị này cho y = 1,645 x 0,69 = 1,14 , như đã giả thiết, chỉ có w9 vượt quá y và hơn nữa việc thay w9* bởi 1,14 cho giá trị w* = 0,63 x 1,097 = 0,69 và lời giải lại tỏ ra hợp lý.
Như vậy ước lượng của độ lệch chuẩn lặp lại là:
![]()
Giá trị này nằm giữa hai ước lượng được cho trong 6.5.2 và 6.5.3.
6.5.5. Bước tiếp theo trong việc phân tích là xác định ước lượng ổn định của độ lệch chuẩn của các trung bình ô. Việc áp dụng thuật toán A đối với các trung bình ô cho ta các kết quả được chỉ ra trong bảng 26. trong đó các trung bình ô được sắp xếp theo thứ tự tăng. Sau bốn bước lặp được chỉ ra trong bảng đó các giá trị ổn định sẽ là x* = 20,412 và s* = 1,1. và chỉ có hai trung bình ô vượt trội (x1* = 17,570: x*9 = 24,140) sai khác với x* một lượng lớn hơn j. Nếu việc tính toán được thực hiện trên máy tính, quá trình đó có thể được tiếp tục cho đến khi sự biến đổi theo x* và s* giữa hai lần lặp liên tiếp là nhỏ.
Nếu việc tính toán được thực hiện bằng tay, người phân tích số liệu cần sử dụng phương pháp trực tiếp đã được mô tả trong 6.2.6 và cần thử với uL = uU = 1, bằng cách đó thu được
x’ = 20,412 và s’ = 0,573 % dầu criôsốt.
Do đó, từ phương trình (62). (63) trong 6.2.6
(s*)2 = 6 x (0,573)2/ [8/1,1342 – 1,52 (9+9-4)/7]
từ đó thu được:
s* = 1,070 % dầu criôsốt
và
x* = x’ = 20,412 % dấu criôsốt.
Có thể khẳng định rằng, giá trị đó của s* sẽ cho j = 1,605 (như đã giả định, chỉ có x1* và x9* là khác với x* = 20,412 một lượng lớn hơn j), và nếu thay x1* bởi 18,807 và x9* bởi 22,017 lại thu được các giá trị mới x* = 20,412 và s* = 0,944 x 1,134 = 1,070. Như vậy lời giải đó tỏ ra là hợp lý.
Từ phương trình (72) trong 6.4.3, thu được ước lượng của độ lệch chuẩn giữa các phòng thí nghiệm là
![]()
và ước lượng độ lệch chuẩn tái lập là
![]()
Một lần nữa, giá trị này nằm giữa hai ước lượng được cho trong 6.5.2 và 6.5.3.
Bảng 24 – Ví dụ 4: Chuẩn độ nhiệt của dầu criôsốt
|
Phòng thí nghiệm i |
Số liệu |
Trung bình ô |
Phạm vi ô |
|
|
1 |
24,28 |
24,00 |
24,140 |
0,28 |
|
2 |
20,40 |
19,91 |
20,155 |
0,49 |
|
3 |
19,30 |
19,70 |
19,500 |
0,40 |
|
4 |
20,30 |
20,30 |
20,300 |
0,00 |
|
5 |
20,53 |
20,88 |
20,705 |
0,35 |
|
6 |
18,56 |
16,58 |
17,570 |
1,98 |
|
7 |
19,70 |
20,50 |
20,100 |
0,80 |
|
8 |
21,10 |
20,78 |
20,940 |
0,32 |
|
9 |
20,71 |
21,66 |
21,185 |
0,95 |
Bảng 25 – Ví dụ 4: Áp dụng thuật toán S đối với các phạm vi ô ( % dầu criôsốt)
|
(v = 1; x = 1,097; h = 1,645) |
|||||
|
Lần lặp |
01) |
1 |
2 |
3 |
4 |
|
y |
– |
0,66 |
0,86 |
1,00 |
1,09 |
|
w1* |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
|
w2* |
0,28 |
0,28 |
0,28 |
0,28 |
0,28 |
|
w3* |
0,32 |
0,32 |
0,32 |
0,32 |
0,32 |
|
w4* |
0,35 |
0,35 |
0,35 |
0,35 |
0,35 |
|
w5* |
0,40 |
0,40 |
0,40 |
0,40 |
0,40 |
|
w6* |
0,49 |
0,49 |
0,49 |
0,49 |
0,49 |
|
w7* |
0,80 |
0,66 |
0,80 |
0,80 |
0,80 |
|
w8* |
0,95 |
0,66 |
0,86 |
0,95 |
0,95 |
|
w9* |
1,98 |
0,66 |
0,86 |
1,00 |
1,09 |
|
w kết hợp |
0,83 |
0,47 |
0,56 |
0,60 |
0,62 |
|
w* mới |
0,40 2) |
0,52 |
0,61 |
0,66 |
0,68 |
|
1) Cột với lần lặp 0 được trích từ bảng 24 sau khi sắp xếp theo thứ tự tăng. 2) 0,40 là phạm vi trung vị [ xem phương trình (64) trong 6.3.3] |
|||||
Bảng 26 – Ví dụ 4 : Áp dụng thuật toán A đối với các trung bình ô ( % dầu criôsốt)
|
Lần lặp |
01) |
1 |
2 |
3 |
4 |
|
j |
– |
1,424 |
1,478 |
1,514 |
1,539 |
|
x* – j |
– |
18,876 |
18,909 |
18,893 |
18,872 |
|
x* + j |
– |
21,724 |
21,865 |
21,921 |
21,950 |
|
x1* |
17,570 |
18,876 |
18,909 |
18,893 |
18,872 |
|
x2* |
19,500 |
19,500 |
19,500 |
19,500 |
19,500 |
|
x3* |
20,100 |
20,100 |
20,100 |
20,100 |
20,100 |
|
x4* |
20,155 |
20,155 |
20,155 |
20,155 |
20,155 |
|
x5* |
20,300 |
20,300 |
20,300 |
20,300 |
20,300 |
|
x6* |
20,705 |
20,705 |
20,705 |
20,705 |
20,705 |
|
x7* |
20,940 |
20,940 |
20,940 |
20,940 |
20,940 |
|
x8* |
21,185 |
21,185 |
21,185 |
21,185 |
21,185 |
|
x9* |
24,140 |
21,724 |
21,865 |
21,921 |
21,950 |
|
Trung bình |
20,511 |
20,387 |
20,407 |
20,411 |
20,412 |
|
Đô lệch chuẩn |
1,727 |
0,869 |
0,890 |
0,905 |
0,916 |
|
x* mới |
20,300 2) |
20,387 |
20,407 |
20,411 |
20,412 |
|
s* mới |
0,949 2) |
0,985 |
1,009 |
1,026 |
1,039 |
|
1) Cột với lần lặp 0 được trích từ bảng 24 sau khi sắp xếp theo thứ tự tăng 2) 20,300 và 0,949 thu được khi sử dụng phương trình (56) và (57) trong 6.2.3 |
|||||
6.6. Các công thức : Phân tích ổn định ở một mức cụ thể của thiết kế mức tách biệt
6.6.1. Với thiết kế mức tách biệt, ước lượng ổn định của độ lệch chuẩn lặp lại sr ở một mức có thể thu được bằng cách áp dụng thuật toán A đối với độ sai khác ô ở mức đó để suy ra giá trị ổn định s*, từ phương trình (61): và sau đó tính sr theo công thức
![]()
6.6.2. Ước lượng ổn định của độ lệch chuẩn của các trung bình ô sy ở một mức có thể thu được bằng cách lại áp dụng thuật toán A đối với các trung bình ô ở mức đó để suy ra giá trị ổn định s* từ phương trình (61) và sau đó thu được sy như sau
![]()
Có thể sử dụng các công thức trong 4.5.6 để tính ước lượng của độ lệch chuẩn tái lập ở mức đó.
6.7. Ví dụ 5: Phân tích ổn định ở một mức cụ thể của thiết kế mức tách biệt
6.7.1. Các số liệu của ví dụ 1 trong 4.8 chứa một số giá trị tản mạn và bất thường (xem bảng 8). Cũng như vậy, hình 3 thể hiện một độ chênh âm nhất quán theo các kết quả của phòng thí nghiệm 5. Nếu không phát hiện ra các nguyên nhân của sự bất bình thường đó, người phân tích số liệu sẽ bị đặt vào tình huống khó xử khi cần quyết định xem số liệu nào phải bị loại khi tính toán độ lệch chuẩn lặp lại và tái lập. Các số liệu ở mức 14 (xem bảng 4) được dùng ở đây để minh họa các kết quả thu được bằng việc phân tích ổn định.
6.7.2. Để nhận được ước lượng ổn định của độ lệch chuẩn lặp lại, ta hãy áp dụng thuật toán A đối với các độ sai khác ô (từ bảng 5). Các kết quả thu được chỉ ra trong bảng 27, trong đó các độ sai khác ô đã được sắp xếp theo thứ tự tăng. Sau bốn lần lặp được chỉ ra trong bảng đó, rõ ràng rằng các giá trị ổn định là x*» 8,29 và s*» 0,36 và chỉ có x9* khác với x* một lượng lớn hơn j.
Việc áp dụng phương pháp đã mô tả trong 6.2.6 với uL = 0, uU = 1 sẽ cho
x’= 8,219 và s’= 0,257 % protein.
như vậy các phương trình (62) và (63) có thể được viết :
x* = 8,219 + 1,5 x s*/8
và
(s*)2 = 7 x (0,257)2/ [8/1,1342 – 1,52(0 + 9 – 0)/ 8]
do đó
s* = 0,354 % protein.
và khi sử dụng phương trình (75) trong 6.6.1 ta được
![]()
Trung bình ổn định của độ sai khác ô là
![]()
Với các giá trị đó của x* và s* thì
j = 1,5 x 0,354 = 0,531
như vậy
x* – j = 7,754 và x* – j = 8,816 % protein.
Như đã giả định, để tính x* va s*, rằng chỉ có x9* nằm ngoài các giới hạn đó. Có thể khẳng định rằng điều đó là đúng và như vậy lời giải thu được là có hiệu lực (chấp nhận được).
6.7.3. Việc áp dụng thuật toán A đối với các trung bình ô (từ bảng 6) cho ta các kết quả trong bảng 28, trong đó các trung bình ô đã được sắp xếp theo thứ tự tăng. Tình huống ở đây tương tự với tình huống được phát hiện ở bảng 26, trong đó x1* và x9* sai khác với x* một lượng lớn hơn j, và x* nằm gần trung bình của các giá trị từ x2* đến x8* tức là giá trị 85,486. Nếu áp dụng một lần nữa phương pháp của 6.2.6 nhưng với uL = uU = 1, giá trị trung bình và độ lệch chuẩn của các giá trị từ x2* đến x8* là :
x’ = 85,486 và s’ = 0,209
Do đó có thể dùng phương trình (63) trong 6.2.6 để suy ra s* từ
(s*)2 = 6 x (0,209)2/ [8/1,1342 – 1,52(9 + 9 – 4 )/ 7]
như vậy
s* = 0,390 % protein.
Bây giờ có thể sử dụng phương trình (62) trong 6.2.6 để nhận được
x* = 85,486 % protein.
Để kiểm tra xem lời giải đó có hiệu lực hay không, hãy tính
j = 1,5 x 0,390 = 0,585
x* – j = 84,901 và x* + j = 86,071 % protein.
Ta thấy rằng, như đã giả thiết, chỉ có x1* và x9* nằm ngoài các giới hạn đó.
Để nhận được độ lệch chuẩn tái lập, sử dụng phương trình (76) trong 6.6.2 để có:
sr = 0,390 % protein.
và sử dụng phương trình (13) trong 4.5.6 để có:
sR = 0,410 % protein.
Do đó, trong ví dụ này, phương pháp ổn định sẽ cho các ước lượng sr và sR nhỏ hơn một chút so với các giá trị thu được khi sử dụng tất cả các số liệu đã báo cáo (cho trong bảng 7).
Bảng 27 – Ví dụ 5 : Áp dụng thuật toán A đối với các độ sai khác ô (% protein)
|
Lần lặp |
01) |
1 |
2 |
3 |
4 |
|
j |
– |
0,53 |
0,56 |
0,55 |
0,54 |
|
x* – j |
– |
7,85 |
7,74 |
7,74 |
7,75 |
|
x* + j |
– |
8,91 |
8,86 |
8,84 |
8,83 |
|
x1* |
7,81 |
7,85 |
7,81 |
7,81 |
7,81 |
|
x2* |
7,93 |
7,93 |
7,93 |
7,93 |
7,93 |
|
x3* |
8,13 |
8,13 |
8,13 |
8,13 |
8,13 |
|
x4* |
8,14 |
8,14 |
8,14 |
8,14 |
8,14 |
|
x5* |
8,38 |
8,38 |
8,38 |
8,38 |
8,38 |
|
x6* |
8,40 |
8,40 |
8,40 |
8,40 |
8,40 |
|
x7* |
8,44 |
8,44 |
8,44 |
8,44 |
8,44 |
|
x8* |
8,52 |
8,52 |
8,52 |
8,52 |
8,52 |
|
x9* |
9,31 |
8,91 |
8,86 |
8,84 |
8,83 |
|
Trung bình |
8,340 |
8,300 |
8,290 |
3,288 |
8,287 |
|
Độ lệch chuẩn |
0,436 |
0,326 |
0,322 |
0,317 |
0,315 |
|
x* mới |
8,380 1) |
8,300 |
8,290 |
8,288 |
8,287 |
|
s* mới |
0,356 1) |
0,370 |
0,365 |
0,359 |
0,357 |
|
1) Thu được khi sử dụng phương trình (56), (57) trong 6.2.3. |
|||||
Bảng 28 – Ví dụ 5: Áp dụng thuật toán A đối với các trung bình ô (% protein)
|
Lần lặp |
01) |
1 |
2 |
3 |
4 |
|
j |
– |
0,446 |
0,492 |
0,519 |
0,537 |
|
x* – j |
– |
85,104 |
85,009 |
84,971 |
84,950 |
|
x* + j |
– |
85,996 |
85,993 |
86,009 |
86,024 |
|
x1* |
84,525 |
85,104 |
85,009 |
84,971 |
84,950 |
|
x2* |
85,140 |
85,140 |
85,140 |
85,140 |
85,140 |
|
x3* |
85,345 |
85,345 |
85,345 |
85,345 |
85,345 |
|
x4* |
85,385 |
85,385 |
85,385 |
85,385 |
85,385 |
|
x5* |
85,550 |
85,550 |
85,550 |
85,550 |
85,550 |
|
x6* |
85,575 |
85,575 |
85,575 |
85,575 |
85,575 |
|
x7* |
85,660 |
85,660 |
85,660 |
85,660 |
85,660 |
|
x8* |
85,750 |
85,750 |
85,750 |
85,750 |
85,750 |
|
x9* |
86,170 |
85,996 |
85,993 |
86,009 |
86,024 |
|
Trung bình |
85,456 |
85,501 |
85,490 |
85,487 |
85,487 |
|
Độ lệch chuẩn |
0,453 |
0,289 |
0,305 |
0,316 |
0,324 |
|
x* mới |
85,550 1) |
85,501 |
85,490 |
85,487 |
85,487 |
|
s* mới |
0,297 1) |
0,328 |
0,346 |
0,358 |
0,367 |
|
1) Thu được khi áp dụng phương trình (56), (57) trong 6.2.3. |
|||||
6.8. Các công thức : Phân tích ổn định ở một mức cụ thể của một thí nghiệm trên vật liệu không đồng nhất
6.8.1. Với thiết kế dùng vật liệu không đồng nhất, trong trường hợp bình thường khi hai mẫu được chuẩn bị cho một trong p’ phòng thí nghiệm ở mỗi mức và hai kết quả thử nghiệm thu được ở mỗi mẫu, các ước lượng ổn định của độ lệch chuẩn lặp lại và tái lập có thể thu được bằng cách áp dụng ba lần các thuật toán A và S như sau
a) Áp dụng thuật toán S đối với phạm vi giữa các giá trị thử nghiệm để dẫn ra một giá trị ổn định w* từ phương trình (67) trong 6.3.4 và tính:
SSr = 2p(w*)2 (77)
b) Áp dụng thuật toán S đối với phạm vi giữa các mẫu để dẫn ra giá trị ổn định khác w* từ phương trình (67) và tính:
SSH=p'(w*)2 (78)
c) Áp dụng thuật toán A đối với trung bình ô để suy ra một giá trị ổn định s* từ phương trình (61) trong 6.2.4 và đặt
sy = s* (79)
Các tính toán đó có thể được sắp đặt một cách tiện lợi dưới dạng bảng, với cột thứ nhất gồm các phạm vi hoặc các trung bình được đưa vào theo thứ tự tăng, như được chỉ ra trong ví dụ dưới đây.
6.8.2. Các công thức nêu ra trong 5.5 có thể được sử dụng để tính các ước lượng của độ lệch chuẩn lặp lại và tái lập và của độ lệch chuẩn sH đo độ thay đổi giữa các mẫu.
6.9. Ví dụ 6 : Phân tích ổn định ở một mức cụ thể của thí nghiệm trên vật liệu không đồng nhất
6.9.1. Các số liệu ở mức 6 của Ví dụ 2 trong 5.8 không chứa bất kỳ giá trị bất thường hoặc tản mạn nào và vì vậy chúng được sử dụng ở đây để minh họa cho các kết quả thu được bằng phương pháp ổn định trong trường hợp đó.
6.9.2. Việc áp dụng thuật toán S đối với phạm vi giữa các kết quả thử nghiệm (từ bảng 14) sẽ cho các kết quả được chỉ ra trong bảng 29. Ở đây bậc tự do v = 1. do đó h = 1,645; x = 1,097 và số các phần tử của số liệu là r = 2r‘ = 22. Sau bốn lần lặp lại được chỉ ra trong bảng 29 giá trị ổn định thu được là w* = 4,5 và w19* đến w22* vượt quá y. Trong trường hợp này, với å’ và uU được xác định như trong 6.3.6 ta có:
uU = 4
å‘(w1*)2/p = 137,92 / 22 = 6,2691.
Như vậy phương trình (68) trong 6.3.6 trở thành
(w*)2 = 1,0972 x 6,2691 + 4(1,097 x 1,645w*)2/22
và do đó
w* = 4,30 %
Có thể khẳng định rằng với giá trị này của w*, y =7,1 và bốn giá trị từ w19* đến w22* đều vượt quá y, như vậy giá trị đó của w* là một lời giải hợp lý.
Việc sử dụng phương trình (77) trong 6.8.1 cho ta
SSr = 22 x 4,302 = 406,78 (%)2
6.9.3. Việc áp dụng thuật toán S lần thứ hai đối với phạm vi giữa các mẫu (từ bảng 15) cho các kết quả được chỉ ra trong bảng 30. Sau bốn lần lặp được chỉ ra trong bảng đó thu được giá trị ổn định w*11 = 4,0 và w10*, w11* vượt quá y. Trong trường hợp này, với å‘ và uL được xác định như trong 6.3.6 thu được
uv = 2
å‘(w1*)2/p’ = 66,665/11 = 6,0605
như vậy phương trình (68) trong 6.3.6 trở thành:
(w*)2 = 1,0972 x 6,0605 + 2(1,097 x 1.645w*)2/11
và do đó
w* = 4,23 %
Đáng tiếc rằng, giá trị này ứng với y = 1,645 x 4,23 = 6,96, do đó lời giải này không hợp lý vì w10* và w11* không vượt quá giá trị đó. Điều này gợi ý rằng lời giải đòi hỏi phải có uU = 1 hoặc uU = 0.
Bằng cách thử cho uU =1 ta có :
å‘(wi*)2/p’ = 112,2275/11 = 10,2025
như vậy phương trình (68) trở thành
(w*)2 = 1,0972 x 10,2025 + (1,097 x 1,645w*)2/11
và từ đó
w* = 4,18 %
Bây giờ y = 1,645 x 4,18 = 6,88 và có thể thấy đó là lời giải hợp lý vì w11* vượt quá 6,88.
Việc sử dụng phương trình (78) trong 6.8.1 cho ta
SSH=11 x 4,182 = 192,20 (%)2
6.9.4. Áp dụng thuật toán A đối với các trung bình ô (từ bảng 16) cho ta các kết quả được chỉ ra trong bảng 31. Việc tính toán sẽ hội tụ sau hai lần lặp và cho ta s* = 5,70 (không có xi* nào khác với x* một lượng lớn hơn j).
Nếu sử dụng phương trình (79) trong 6.8.1 thu được:
sy = 5,70 %
6.9.5. Nếu kết hợp các kết quả thu được trong 6.9.2, 6.9.3, 6.9.4. các phương trình (29) đến (33) trong 5.5.5 có:
sr2 = 406,78 / 44 (%) 2
SR2 = 5,702 + (406,78 – 192,20)/ 44 (%)2
sH2 = 192,20 / 22 – 406,78 / 88 (%)2.
do đó
sy = 3,04 %
sR = 6,11 %
sH = 2,03%
Do đó trong ví dụ này, phương pháp ổn định cho các ước lượng sr, sR, sH lớn hơn các giá trị thu được khi sử dụng tất cả các số liệu đã được báo cáo (cho trong 5.8.3 và bảng 17).
Bảng 29 – Ví dụ 6: Áp dụng thuật toán S đối với phạm vi giữa các kết quả thử nghiệm
(v = 1; x = 1,097; h = 1,645)
|
Lần lặp |
0 |
1 |
2 |
3 |
4 |
|
y |
– |
3,9 |
5,1 |
5,9 |
6,4 |
|
w1* |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
|
w2* |
0,6 |
0,6 |
0,6 |
0,6 |
0,6 |
|
w3* |
1,1 |
1,1 |
1,1 |
1,1 |
1,1 |
|
w4* |
1,1 |
1,1 |
1,1 |
1,1 |
1,1 |
|
w5* |
1,2 |
1,2 |
1,2 |
1,2 |
1,2 |
|
w6* |
1,3 |
1,3 |
1,3 |
1,3 |
1,3 |
|
w7* |
1,4 |
1,4 |
1,4 |
1,4 |
1,4 |
|
w8* |
1,6 |
1,6 |
1,6 |
1,6 |
1,6 |
|
w9* |
1,8 |
1,8 |
1,8 |
1,8 |
1,8 |
|
w10* |
2,1 |
2,1 |
2,1 |
2,1 |
2,1 |
|
w11* |
2,2 |
2,2 |
2,2 |
2,2 |
2,2 |
|
w12* |
2,5 |
2,5 |
2,5 |
2,5 |
2,5 |
|
w13* |
2,6 |
2,6 |
2,6 |
2,6 |
2,6 |
|
w14* |
3,9 |
3,9 |
3,9 |
3,9 |
3,9 |
|
w15* |
4,0 |
3,9 |
4,0 |
4,0 |
4,0 |
|
w16* |
4,4 |
3,9 |
4,4 |
4,4 |
4,4 |
|
w17* |
4,6 |
3,9 |
4,6 |
4,6 |
4,6 |
|
w18* |
5,5 |
3,9 |
5,1 |
5,5 |
5,5 |
|
w19* |
7,4 |
3,9 |
5,1 |
5,9 |
6,4 |
|
w20* |
7,6 |
3,9 |
5,1 |
5,9 |
6,4 |
|
w21* |
8,1 |
3,9 |
5,1 |
5,9 |
6,4 |
|
w22* |
8,1 |
3,9 |
5,1 |
5,9 |
6,4 |
|
w mới |
4,17 |
2,80 |
3,29 |
3,55 |
3,70 |
|
w* mới |
2,35 1) |
3,07 |
3,61 |
3,89 |
4,06 |
|
1) Thu được khi sử dụng phương trình (64) trong 6.3.3 |
|||||
Bảng 30 – Ví dụ 6: Áp dụng thuật toán S đối với các phạm vi giữa các mẫu (%)
|
(v = 1; x = 1,097; h = 1,645) |
|||||
|
Lần lặp |
0 |
1 |
2 |
3 |
4 |
|
y |
|
4,19 |
5,43 |
6,10 |
6,45 |
|
w1* |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
|
w2* |
1,70 |
1,70 |
1,70 |
1,70 |
1,70 |
|
w3* |
2,05 |
2,05 |
2,05 |
2,05 |
2,05 |
|
w4* |
2,25 |
2,25 |
2,25 |
2,25 |
2,25 |
|
w5* |
2,55 |
2,55 |
2,55 |
2,55 |
2,55 |
|
w6* |
2,55 |
2,55 |
2,55 |
2,55 |
2,55 |
|
w7* |
3,15 |
3,15 |
3,15 |
3,15 |
3,15 |
|
w8* |
3,35 |
3,35 |
3,35 |
3,35 |
3,35 |
|
w9* |
4,40 |
4,19 |
4,40 |
4,40 |
4,40 |
|
w10* |
6,75 |
4,19 |
5,43 |
6,10 |
6,45 |
|
w11* |
6,95 |
4,19 |
5,43 |
6,10 |
6,45 |
|
w mới |
3,82 |
3,01 |
3,38 |
3,58 |
3,69 |
|
w* mới |
2,55 1) |
3,30 |
3,71 |
3,92 |
4,05 |
|
1) Thu được khi sử dụng phương trình (64) trong 6.3.3 |
|||||
Bảng 31 – Ví dụ 4 : Áp dụng thuật toán A đối với các trung bình ô ( %)
|
Lần lặp |
0 |
1 |
2 |
3 |
4 |
|
j |
– |
10,005 |
8,550 |
|
|
|
x* – j |
– |
8,245 |
10,450 |
|
|
|
x* + j |
– |
28,255 |
27,550 |
|
|
|
x1* |
13,425 |
13,425 |
13,425 |
|
|
|
x2* |
13,425 |
13,425 |
13,425 |
|
|
|
x3* |
13,750 |
13,750 |
13,750 |
|
|
|
x4* |
14,475 |
14,475 |
14,475 |
|
|
|
x5* |
17,075 |
17,075 |
17,075 |
|
|
|
x6* |
18,250 |
18,250 |
18,250 |
|
|
|
x7* |
21,000 |
21,000 |
21,000 |
|
|
|
x8* |
21,225 |
21,225 |
21,225 |
|
|
|
x9* |
23,675 |
23,675 |
23,675 |
|
|
|
x10* |
26,275 |
26,275 |
26,275 |
|
|
|
x11* |
26,425 |
26,425 |
26,425 |
|
|
|
Trung bình |
19,00 |
19,00 |
19,00 |
|
|
|
Độ lệch chuẩn |
5,03 |
5,03 |
5,03 |
|
|
|
x* mới |
18,25 1) |
19,00 |
19,00 |
|
|
|
s* mới |
6,67 1) |
5,70 |
5,70 |
|
|
|
1) Thu được khi sử dụng phương trình (56) và (57) trong 6.2.3 |
|||||
PHỤ LỤC A
(quy định)
CÁC KÝ HIỆU VÀ CHỮ VIẾT TẮT DÙNG TRONG TCVN 6910
|
u |
Phần bị chắn trong mối quan hệ s = a + bm |
|
A |
Yếu tố dùng để tính độ không đảm bảo của ước lượng |
|
b |
Độ dốc trong mối quan hệ s = a + bm |
|
B |
Thành phần trong kết quả thử nghiệm biểu thị độ lệch của phòng thí nghiệm so với trung bình chung (thành phần phòng thí nghiệm của độ chệch) |
|
Bo |
Thành phần của B biểu thị tất cả các yếu tố không thay đổi trong điều kiện chụm trung gian |
|
B(1), B(2)…. |
Các thành phần của B biểu thị những yếu tố thay đổi trong điều kiện chụm trung gian |
|
c |
Phần bị chắn trong mối quan hệ lg s = c + d lg m |
|
C, C’, C” |
Các thống kê kiểm nghiệm |
|
Ccrit, C’crit, C”crit |
Các giá trị tới hạn đối với những phép kiểm nghiệm thống kê |
|
CDP |
Độ sai khác tới hạn với xác suất P |
|
CRP |
Phạm vi tới hạn với xác suất P |
|
d |
Độ dốc trong mối liên hệ lg s = c + d lg m |
|
e |
Thành phần trong kết quả thử nghiệm biểu thị sai số ngẫu nhiên tồn tại trong mọi kết quả thử nghiệm |
|
f |
Yếu tố phạm vi tới hạn |
|
Fp(v1, v2) |
Phân vị mức p của phân bố F với các bậc tự do v1 và v2 |
|
G |
Thống kê kiểm nghiệm Grubb |
|
h |
Thống kê kiểm nghiệm nhất quán giữa các phòng thí nghiệm của Mandel |
|
k |
Thống kê kiểm nghiệm nhất quán trong phòng thí nghiệm của Mandel |
|
LCL |
Giới hạn kiểm soát dưới (hoặc giới hạn hành động hoặc giới hạn cảnh báo) |
|
m |
Trung bình chung của đặc tính thử; mức |
|
M |
Yếu tố được xem xét trong điều kiện chụm trung gian |
|
N |
Số phép lặp |
|
n |
Số kết quả thử nghiệm thu được của phòng thí nghiệm tại một mức |
|
p |
Số phòng thí nghiệm tham gia thí nghiệm liên phòng |
|
P |
Xác suất |
|
q |
Số lượng các mức của đặc tính thử nghiệm trong thí nghiệm liên phòng |
|
r |
Giới hạn lặp lại |
|
R |
Giới hạn tái lập |
|
RM |
Mẫu chuẩn |
|
s |
Ước lượng của độ lệch chuẩn |
|
|
Độ lệch chuẩn dự đoán |
|
T |
Tổng thể hoặc tổng của biểu thức nào đó |
|
t |
Số các đối tượng thử nghiệm hoặc số nhóm |
|
UCL |
Giới hạn kiểm soát trên (hoặc giới hạn hành động hoặc giới hạn cảnh báo) |
|
W |
Yếu tố trọng số sử dụng trong tính toán hồi quy trọng số |
|
w |
Độ rộng của tập hợp các kết quả thử nghiệm |
|
x |
Dữ liệu sử dụng cho thử nghiệm Grubb |
|
y |
Kết quả thử nghiệm |
|
|
Trung bình số học của kết quả thử nghiệm |
|
|
Trung bình chung của kết quả thử nghiệm |
|
a |
Mức ý nghĩa |
|
b |
Xác suất sai lầm loại II |
|
g |
Tỷ số giữa độ lệch chuẩn tái lập và độ lệch chuẩn lặp lại (sR/sr) |
|
D |
Độ chệch phòng thí nghiệm |
|
|
Ước lượng của D |
|
d |
Độ chệch của phương pháp đo |
|
|
Ước lượng của d |
|
l |
Sự sai khác phát hiện được giữa các độ chệch của hai phòng thí nghiệm hoặc các độ chệch của hai phương pháp đo |
|
m |
Giá trị thực hoặc giá trị quy chiếu được chấp nhận của đặc tính thử nghiệm |
|
n |
Số bậc tự do |
|
r |
Tỷ số phát hiện được giữa độ lệch chuẩn lặp lại của phuơng pháp B và phương pháp A |
|
s |
Giá trị thực của độ lệch chuẩn |
|
t |
Thành phần của kết quả thử nghiệm biểu thị sự thay đổi theo thời gian từ lần hiệu chuẩn cuối cùng |
|
f |
Tỷ số phát hiện được giữa căn bậc hai của bình phương trung bình giữa các phòng thí nghiệm của phương pháp B và phương pháp A |
|
c2r(n) |
Phân vị mức r của phân bố c2với bậc tự do n |
Các ký hiệu được sử dụng như chỉ số
|
C |
Sự khác nhau về hiệu chuẩn |
|
E |
Sự khác nhau về thiết bị |
|
i |
Chỉ số của một phòng thí nghiệm cụ thể |
|
I( ) |
Chỉ số của thước đo trung gian của độ chụm, trong dấu ngoặc chỉ loại tình huống trung gian |
|
j |
Chỉ số của một mức cụ thể (TCVN 6910-2 (ISO 5725-2)) |
|
|
Chỉ số của một nhóm phép thử nghiệm hoặc một yếu tố (TCVN 6910-3) |
|
k |
Chỉ số của một kết quả thử nghiệm cụ thể trong phòng thí nghiệm / ở mức j |
|
L |
Liên phòng thí nghiệm (liên phòng) |
|
m |
Chỉ số của độ chệch có thể biết được |
|
M |
Mẫu thử liên phòng |
|
O |
Sự khác nhau về người thao tác |
|
P |
Xác suất |
|
r |
Độ lặp lại |
|
R |
Độ tái lập |
|
T |
Sự khác nhau về thời gian |
|
W |
Phòng thí nghiệm thành viên |
|
1,2,3 … |
Đối với các kết quả thử nghiệm, đánh số theo thứ tự thu nhận chúng |
|
(1), (2), (3)… |
Đối với các kết quả thử nghiệm, đánh số theo thứ tự tăng độ lớn |
Các ký hiệu và chữ viết tắt dùng trong TCVN 6910-5 : 2002
|
D |
Độ sai khác trong ô của thiết kế mức tách biệt |
|
g |
Số mẫu thử nghiệm trong một phòng thí nghiệm ở một mức. |
|
H |
Thành phần trong kết quả đo biểu thị sai số ngẫu nhiên của mẫu. |
|
K |
Hàm số các kết quả đo trong ô |
|
p’ |
Số các phòng thí nghiệm tham gia trong thí nghiệm liên phòng |
|
SS |
Tổng các bình phương |
|
uL |
Số các giá trị của dữ liệu nhỏ hơn giới hạn dưới trong phân tích ổn định |
|
uU |
Số các giá trị của dữ liệu lớn hơn giới hạn trên trong phân tích ổn định |
|
z |
Phần dư |
|
F |
Tỷ số của các độ lệch chuẩn. |
|
j |
Giới hạn được dùng trong phân tích ổn định (thuật toán A) |
|
h |
Thừa số giới hạn được dùng trong phân tích ổn định (thuật toán S) |
|
y |
Giới hạn được dùng trong phân tích ổn định (thuật toán S) |
|
x |
Thừa số hiệu chỉnh sử dụng trong phân tích ổn định (thuật toán S) |
Các ký hiệu phụ thêm dùng làm chỉ số trong TCVN 6910 – 5:2002
|
a,b |
Chỉ số phân biệt các mẫu trong thí nghiệm mức tách biệt |
|
t |
Chỉ số phân biệt một mẫu trong phòng thí nghiệm i ở mức j |
|
H |
Giữa các mẫu |
Các ký hiệu phụ thêm được sử dụng như chỉ số trong TCVN 6910-5 : 2002
|
* |
Ước lượng ổn định |
PHỤ LỤC B
(tham khảo)
DẪN RA CÁC THỪA SỐ SỬ DỤNG TRONG THUẬT TOÁN A VÀ S
B.1. Mở đầu
Việc sử dụng phương pháp ổn định để phân tích số liệu của các thí nghiệm độ chụm đã được đề suất bởi Hội đồng về các phương pháp phân tích của Hội Hóa học Hoàng gia Anh (UK) xem [6]. Thuật toán A trong tiêu chuẩn này được dẫn ra từ bài báo của họ và thừa số 1,134 dùng để tính s* trong thuật toán A cũng được lấy ra từ bài báo của họ (đó là giá trị 1/ cho trường hợp c = 1,5 theo ký hiệu của bài báo đó )
“Thuật toán S” là thủ tục tương tự với thủ tục được đưa ra trong [6] cho trường hợp đặc biệt, trong đó mỗi phòng thí nghiệm báo cáo n = 2 lần đo ở một mức. Nó đưa ra một phương pháp tiện lợi cho việc áp dụng việc phân tích ổn định đối với các thí nghiệm độ chụm với nhiều hơn hai thừa số (như thiết kế với các vật liệu không đồng nhất trong điều 5 của tiêu chuẩn này và thiết kế xếp chồng so le của TCVN 6910 -3.). Việc dẫn ra các thừa số sử dụng trong thuật toán S được thực hiện dưới đây.
B.2. Các ký hiệu sử dụng trong phụ lục này
|
s |
độ lệch chuẩn thực |
|
s |
độ lệch chuẩn ước lượng của s |
|
n |
bậc tự do của s |
|
w |
n + 2 |
|
x |
Thừa số hiệu chính của thuật toán S |
|
h |
Thừa số giới hạn của thuật toán S |
|
cn2 |
Biến khi – bình phương với n bậc tự do |

B.3. Dẫn ra các thừa số giới hạn h và thừa số hiệu chính x
Thừa số hiệu chính x được định nghĩa như là giá trị cần thiết để hiệu chính s* sao cho (s*)2 cho ta một ước lượng không chệch của s2 tức là:

Yêu cầu đó có thể được viết dưới dạng

trong đó các đại lượng trong ngoặc { } có liên quan chặt chẽ với đại lượng n (s/s)2, biến khi – bình phương, cn2
Hàm mật độ xác suất của biến khi – bình phương cn2 là:
![]()
như vậy

vì s £hs tương đương với n(s /s)2£nh2
Số hạng thứ hai trong về phải của B4 là:
![]()
Đối với thuật toán S, thừa số giới hạn h được chọn sao cho hs là điểm ở trên mức 10 % của phân số s, tức là điểm sao cho:
![]()
Các bảng Biometrica (sinh trắc) của phân bố khi – bình phương cho ta các giá trị của h ở trong bảng 23 tiêu chuẩn này. Từ các phương trình (B5), (86) suy ra rằng thành phần thứ hai của vế phải của (B4) là 0,1 nh2. Chú ý rằng h phụ thuộc vào bậc tự do của s
Thành phần thứ nhất của (B4) có thể viết:
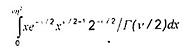
Theo tính chất của hàm gama với w = n + 2 ta có

như vậy số hạng đầu đó trở thành:

Như vậy, với số bậc tự do n đã cho, h có thể tính như trên và sau đó cũng tính được z khi sử dụng bảng phân bố khi – bình phương cho trong các bảng Biometrika. Như vậy cả hai ở vế phải của (B4) có thể xác định được.
Nếu thay các phương trình (B2) đến (B7) vào (B4) ta được.
![]()
hoặc
![]()
Hệ thức này dùng để thu được các giá trị của thừa số hiệu chỉnh x cho trong bảng 23 của tiêu chuẩn này.
PHỤ LỤC C
(tham khảo)
DẪN RA CÁC PHƯƠNG TRÌNH DÙNG ĐỂ PHÂN TÍCH ỔN ĐỊNH
Các phương trình (62) và (63) dùng để tính các giá trị ổn định của trung bình và độ lệch chuẩn bằng phương pháp đã mô tả trong 6.2.6 có thể được suy ra từ phương trình (60) và (61) trong 6.2.4 (Thuật toán A) như sau:
Với các ký hiệu như trong 6.2.4 và 6.2.6

và

trong đó S‘ biểu thị tổng lấy trên (p – uL – uU) các số hạng x1 của số liệu sao cho |x1 – x1*| £j
Do đó có thể viết phương trình (C1) như sau:
![]()
như vậy
![]()
và từ đó:
![]()
đó chính là phương trình (62) trong 6.2.6.
Để suy ra phương trình (63) từ phương trình (61), chú ý rằng có thể khai triển tổng trong phương trình (61) như sau.
![]()
Nếu thay x* trong số hạng tổng ở đây bởi vế phải của (C4), sau một số tính toán đại số ta thu được:

Nếu sử dụng định nghĩa của s’ trong (C3), tổng trên có thể viết thành:
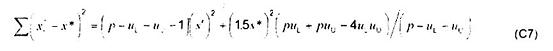
Sau đó nếu thay phương trình (C7) vào phương trình (61) ta thu được phương trình (63).
PHỤ LỤC D
(tham khảo)
Tài liệu tham khảo
[1] BS 812-103:1985, Testing aggregates – Part 103. Methods for determination of particle siz distribution. British Standards Institution. [2] BS 812-121:1989, Testing aggregates – Part 121: Methods for determination of soundness. Britisl Standards Institution. [3] BS 3144:1968, Methods of sampling and physical testing of leather. British Standards Institution. [4] Scheffé, H. The analysis of variance. Wiley, New York, 1959. [5] Sweeney, An inter-laboratory study of the determination of protein by combustion in feeds. Journal of the Association of Official Analytical Chemists, 72, 1989, pp. 770-774. [6] Analytical Methods Committee. Robust statistics – How not to reject outliers. Part 1: Basic concepts Part 2: Inter-laboratory trials. The Analyst, 114, 1989, pp. 1653-1697 (part 1), pp. 1699-1702 (part 2) Royal Society of Chemistry, London. [7] Youden, W.J. The Youden plot. Industrial Quality Control, 15, 1959, pp. 133-137. [8] Mandel, J and Lashof, T.W. Interpretation and Generalization of Youden’s Two-Sample Diagram. Journal of Quanlity Technology, 6, 1974, pp. 22-36.
MỤC LỤC
Lời giới thiệu
1. Phạm vi áp dụng
2. Tiêu chuẩn viện dẫn
3. Định nghĩa
4. Thiết kế mức tách biệt
4.1. Các ứng dụng của thiết kế mức tách biệt
4.2. Bố trí thiết kế mức tách biệt
4.3. Tổ chức thí nghiệm mức tách biệt
4.4. Mô hình thống kê
4.5. Phân tích thống kê các số liệu từ thí nghiệm mức tách biệt
4.6. Khảo sát sự phù hợp và bất thường của các số liệu
4.7. Báo cáo kết quả thí nghiệm mức tách biệt
4.8. Ví dụ 1: Thí nghiệm mức tách biệt – Xác định protein
5. Thiết kế cho các vật liệu không đồng nhất
5.1. Ứng dụng các thiết kế cho các vật liệu không đồng nhất
5.2. Bố trí thiết kế các vật liệu không đồng nhất
5.3. Tổ chức thí nghiệm với vật liệu không đồng nhất
5.4. Mô hình thống kê cho một thí nghiệm với vật liệu không đồng nhất
5.5. Phân tích thống kê các số liệu từ một thí nghiệm với vật liệu không đồng nhất
5.6. Khảo sát sự phù hợp và sự bất thường của các số liệu
5.7. Báo cáo kết quả của một thí nghiệm trên vật liệu không đồng nhất
5.8. Ví dụ 2: Thí nghiệm trên vật liệu không đồng nhất
5.9. Các công thức tổng quát để tính toán với thiết kế cho vật liệu không đồng nhất
5.10. Ví dụ 3: Áp dụng các công thức tổng quát
6. Phương pháp ổn định để phân tích số liệu
6.1. Áp dụng các phương pháp ổn định để phân tích số liệu
6.2. Phân tích ổn định: Thuật toán A
6.3. Phân tích ổn định: Thuật toán S
6.4. Các công thức: Phân tích ổn định ở một mức cụ thể của thiết kế đồng mức
6.5. Ví dụ 4: Phân tích ổn định ở một mức cụ thể của thiết kế đồng mức
6.6. Các công thức: Phân tích ổn định ở một mức cụ thể của thiết kế mức tách biệt
6.7. Ví dụ 5: Phân tích ổn định ở một mức cụ thể của thiết kế mức tách biệt
6.8. Các công thức: Phân tích ổn định ở một mức cụ thể của thí nghiệm trên vật liệu không đồng nhất
6.9. Ví dụ 6: Phân tích ổn định ở một mức cụ thể của thí nghiệm trên vật liệu không đồng nhất
Phụ lục A (quy định) Các kí hiệu và chữ viết tắt dùng trong TCVN 6910
Phụ lục B (tham khảo) Dẫn ra các thừa số sử dụng trong thuật toán A và S
Phụ lục C (tham khảo) Dẫn ra các phương trình dùng để phân tích ổn định
Phụ lục D (tham khảo) Tài liệu tham khảo