Nội dung toàn văn Tiêu chuẩn quốc gia TCVN 7298:2003 (ISO 497: 1973) về Hướng dẫn lựa chọn dãy số ưu tiên và dãy các giá trị quy tròn của số ưu tiên
TIÊU CHUẨN QUỐC GIA
TCVN 7298: 2003
ISO 497: 1973
HƯỚNG DẪN LỰA CHỌN DÃY SỐ ƯU TIÊN VÀ DÃY CÁC GIÁ TRỊ QUY TRÒN CỦA SỐ ƯU TIÊN
Guide to the choice of series of preferred numbers and of series containing more rounded values of preferred numbers
Lời nói đầu
TCVN 7298: 2003 hoàn toàn tương đương với ISO 497: 1973.
TCVN 7298: 2003 do Tiểu ban kỹ thuật tiêu chuẩn TCVN/TC/SC1 Những vấn đề chung về cơ khí biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ ban hành.
Tiêu chuẩn này được chuyển đổi năm 2008 từ Tiêu chuẩn Việt Nam cùng số hiệu thành Tiêu chuẩn Quốc gia theo quy định tại khoản 1 Điều 69 của Luật Tiêu chuẩn và Quy chuẩn kỹ thuật và điểm a khoản 1 Điều 6 Nghị định số 127/2007/NĐ-CP ngày 1/8/2007 của Chính phủ quy định chi tiết thi hành một số điều của Luật Tiêu chuẩn và Quy chuẩn kỹ thuật.
HƯỚNG DẪN LỰA CHỌN DÃY SỐ ƯU TIÊN VÀ DÃY CÁC GIÁ TRỊ QUY TRÒN CỦA SỐ ƯU TIÊN
Guide to the choice of series of preferred numbers and of series containing more rounded values of preferred numbers
1. Phạm vi áp dụng
Tiêu chuẩn này đưa ra các hướng dẫn bổ sung để hoàn thiện những hướng dẫn đã nêu ở TCVN 7299:2003 về lựa chọn các dãy số ưu tiên và khả năng sử dụng các giá trị quy tròn của số ưu tiên như đề cập ở điều 6 của tiêu chuẩn này
a) Chỉ quy định các giá trị quy tròn có thể chấp nhận được dưới dạng hai dãy giá trị quy tròn ở mức độ lớn hơn hoặc nhỏ hơn;
b) Quy định các điều kiện sử dụng các giá trị quy tròn và hệ quả của việc sử dụng các giá trị này;
c) Đưa ra các quy tắc để có thể tránh được sự thay đổi trong việc lựa chọn giữa các số ưu tiên và các giá trị quy tròn khác nhau.
2. Tiêu chuẩn trích dẫn
TCVN 142: 1988 (ISO 3: 1973) Số ưu tiên – Dãy số ưu tiên.
TCVN 7299: 2003 (ISO 17: 1978) Hướng dẫn sử dụng số ưu tiên và dãy số ưu tiên.
3. Lợi ích của việc sử dụng triệt để các số ưu tiên
Lợi ích của việc sử dụng triệt để các số ưu tiên nêu trong TCVN 142: 1988 và TCVN 7299:2003, được nhắc lại và nhấn mạnh như sau:
Các lợi ích thu được không chỉ trong lĩnh vực tiêu chuẩn hóa của bản thân các chi tiết máy khác nhau mà trước hết là trong kết cấu của các máy hoàn chỉnh khi các đặc tính về chức năng (trong vận hành) cũng như các kích thước hoặc mỗi chi tiết máy khác nhau tuân theo cấp số nhân.
3.1. Cấp số tốt nhất
Các số ưu tiên đảm bảo cho cấp số tốt nhất theo quan điểm về độ đều đặn và khả năng sử dụng thích hợp các số ưu tiên đối với các yêu cầu mới để tạo ra dãy số có giá trị bằng cách chèn thêm vào các giá trị trung gian.
3.2. Khả năng ứng dụng rộng rãi
Số ưu tiên là phương tiện hợp lý nhất để bao quát liên tục toàn bộ phạm vi yêu cầu trong một lĩnh vực đã cho (công suất động cơ, lưu lượng của bơm v.v…).
3.3. Đơn giản hóa các tính toán về kỹ thuật và thương mại
Vì các tích số và thương số của các số ưu tiên cũng là những số ưu tiên nên những tính toán được tiến hành bằng cách sử dụng các giá trị lôgarit hoặc các số thứ tự và bản thân chúng không phải là các số ưu tiên, được coi là đơn giản hóa, đặc biệt là khi dãy các giá trị (kích thước, giá theo bảng chào hàng v.v …) được nhân hoặc chia theo cùng một tỷ lệ.
3.4. Chuyển đổi sang các hệ thống đo lường khác
Sự chuyển đổi sang các hệ thống đo lường khác rất dễ dàng khi dãy các giá trị có số đo được biểu thị bằng các số ưu tiên và đồng thời các hệ số chuyển đổi xấp xỉ với các số ưu tiên.
4. Sử dụng ngoại lệ các giá trị quy tròn
4.1. Trong một số ứng dụng, có một số lý do bắt buộc không cho phép sử dụng các số ưu tiên.
a) Vì không thể hoặc không nhất thiết phải giữ lại tất cả các chữ số có nghĩa, đặc biệt là khi cần đến một số nguyên (ví dụ như 32 thay cho 31,5 đối với số răng của một bánh răng);
b) Bởi vì, trong trường hợp không có chỉ dẫn dung sai, số các chữ số có nghĩa tạo ra ấn tượng về độ chính xác không mong muốn hoặc không thể đo được (ví dụ như 1/30 giây thay cho 1/31,5 giây đối với thời gian lộ sáng của máy ảnh, hoặc 224 đối với một công suất mà trong thực tế cho phép có sai lệch đến khoảng 10 %).
4.2. Trong quá trình biến đổi, có thể có một số ngành công nghiệp hoặc dịch vụ công cộng không chấp nhận các số ưu tiên vì các lý do:
a) Về tính kinh tế (ví dụ như muốn tiếp tục sử dụng các công cụ và dụng cụ đo hiện có trong các nhà máy);
b) Về mặt tâm lý (ví dụ như muốn sử dụng các giá trị được biểu thị bằng cách đơn giản hơn, đặc biệt là trong trường hợp khó viết hoặc đọc các chữ số của số ưu tiên[1]).
4.3. Việc sử dụng các giá trị quy tròn, do đó có thể được giải thích bởi các lý do bắt buộc (xem 4.1) và nên sử dụng các giá trị quy tròn này còn hơn là loại bỏ hoàn toàn cùng với việc sử dụng các số ưu tiên.
Mặt khác, không nên cho phép sử dụng các giá trị quy tròn vì lý do kinh tế hoặc tâm lý (xem 4.2); vì đây là các lý do chủ quan và có thể không giống nhau ở mọi nơi, chúng có thể làm gia tăng các tiêu chuẩn công ty hoặc các tiêu chuẩn nhà nước khác biệt với nhau, làm khó khăn hơn cho sự thống nhất hóa trong phạm vi quốc gia hoặc quốc tế.[2])
5. Quy tắc và bảng chung
Quy tắc: xem quy tắc trong điều 4 của TCVN 7299: 2003
5.1. Khi lựa chọn một nhóm các trị số để đáp ứng các yêu cầu riêng của ứng dụng đang được xem xét:
1) Chọn công bội thích hợp theo thứ tự các chỉ số
5 – 10 – 20 – 40
2) Chọn dãy số có độ chính xác thích hợp cho các giá trị (xem phụ lục, điều A.1.1) và độ đồng đều của công bội (xem phụ lục, điều A.1.2), nghĩa là:
a) ưu tiên chọn các dãy R của bản thân các số ưu tiên * * *;
b) Các dãy số R’ được quy tròn lần thứ nhất, nếu các lý do bắt buộc không cho phép sử dụng các số ưu tiên * *;
c) Hoặc các dãy R” được quy tròn lần thứ hai trong phương án cuối cùng *.
5.2. Khi lựa chọn một giá trị đơn (đơn trị), ví dụ như để xác lập một mẫu đầu tiên, cần nhớ rằng giá trị này có thể được đưa vào một dãy số, sau đó, công bội của dãy số sẽ được giả định và theo 5.1, lựa chọn một số ưu tiên, hoặc nếu không chọn được số ưu tiên thì chọn một giá trị quy tròn.
6. Những tác hại của việc sử dụng các giá trị quy tròn
6.1. Sự có mặt trong dãy số của một giá trị quy tròn duy nhất hoặc một giá trị ngoại lệ đã chấp nhận do sự vi phạm quy tắc và giá trị đó không phải là số ưu tiên có thể làm cho dãy số không thể chuyển đổi tiếp thành một dãy số có công bội nhỏ hơn.
6.2. Sự phân bậc của dãy số gồm các giá trị quy tròn không có lợi bằng sự phân bậc của dãy số ưu tiên vì đối với một vài khoảng, độ không đều đặn có thể đạt tới 2,94 % trong dãy số R’ và thậm chí đến 5,61 % trong dãy số R” (xem các giá trị ở cuối các cột của bảng.1)
* Các dãy số R” này (các giá trị trong ngoặc đơn) và đặc biệt nhất là giá trị 1,5 cần được tránh sử dụng khi ….. các mối nguy hiểm được giải thích trong điều 6.
** Trong trường hợp ngoại lệ, khi một dãy số không cần có sự hồi quy trong phạm vi ứng dụng yêu cầu có sự phân bậc đơn giản của các giá trị không có liên quan đến các dữ liệu khác, và không áp dụng được bản thân các số ưu tiên thì cho phép có sự thay thế giá trị 1,15 cho 1,18 và 1,20 cho 1,25 khi bắt đầu một dãy số
1 – 1,05 – 1,10 – 1,15 – 1,20 – 1,30
*** Trong một số trường hợp ngoại lệ (ví dụ như để chế tạo các cánh tua bin), khi cần đến độ chính xác rất cao thì cho phép sử dụng các giá trị tính toán (cột 6 của bảng).
1) Ví dụ: độ chênh lệch 5 % về kích thước độ dài dẫn đến độ chênh lệch lớn hơn 10 % về diện tích (mặt cắt ngang, ảnh hưởng đến độ bền của bulông; mặt cắt ngang của pittông, ảnh hưởng đến công suất động cơ:
lớn hơn 15 % về thể tích (khối lượng chi tiết, độ uốn cong của trục);
lớn hơn 20 % về lũy thừa bậc 4 (độ cứng của lò xo);
lớn hơn 25 % về lũy thừa bậc 5 (momen quán tính).
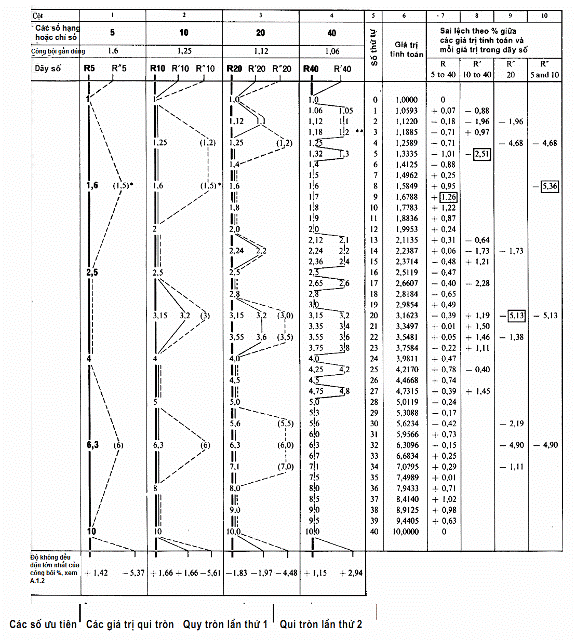
6.3. Sự phân bậc của các dãy số dẫn xuất có thể kém đồng đều hơn so với phân bậc của các dãy số R’ hoặc R” tương ứng, nếu hai giá trị liền kề nhau đã được quy tròn về phía nhau, ví dụ, một giá trị được quy tròn xuống và giá trị kia được quy tròn lên, do đó đối với ví dụ dãy R’ 40/4 (…..1,05…..), độ không đều đặn giữa 1,32 và 1,7 đạt tới 1,26 % + 2,51 % = 3,77 % trong khi độ không đều đặn lớn nhất của dãy ban đầu R’ 40 chỉ là 2,94 %; như vậy, nguyên lý cơ bản về tính quy luật (tính đều đặn) của dãy số ưu tiên bị phá vỡ.
6.4. Mức độ chính xác của các giá trị quy tròn không cao bằng mức độ chính xác của các số ưu tiên. Thực tế, độ không chính xác này có thể đạt tới 2,51 % đối với các giá trị trong dãy R’ và 5,36 % đối với các giá trị trong R”. Hơn nữa, vì thực tế này, không thể sử dụng các giá trị quy tròn cho các đề án kỹ thuật khi tính toán (xem điều 5 của TCVN 7299: 2003) với sự trợ giúp của các số thứ tự cho trong cột 5 của bảng. [3])
6.5. Sự công tác trên phạm vi quốc gia và quốc tế về tiêu chuẩn hóa sẽ khó khăn hơn, nếu thay cho việc sử dụng các số ưu tiên lại chọn các giá trị quy tròn khác nhau để giải quyết cùng một vấn đề[4].
Phụ lục A
(quy định)
Độ chính xác của các giá trị và tính đều đặn của công bội
A.1. Định nghĩa
Để hiểu được những bất lợi và những tác hại của việc sử dụng các giá trị quy tròn và để chỉ sử dụng chúng khi đã hiểu đầy đủ về những bất lợi và những tác hại đó, điều quan trọng trước tiên là phải xét xem thế nào gọi là mức đó chính xác so với giá trị lý thuyết tương ứng:
– Của các giá trị tính toán;
– Của các số ưu tiên;
– Của các giá trị quy tròn;
– Mức độ đều đặn công bội của các dãy số tương ứng.
A.1.1. Mức độ chính xác của một số hạng [5]) so với giá trị lý thuyết tương ứng được đặc trưng bởi mối quan hệ, biểu thị bằng phần trăm.
– của hiệu số giữa giá trị đang xét và giá trị lý thuyết;
– với giá trị lý thuyết này.
Các hiệu số tương đối này được cho đối với các số ưu tiên trong cột 8 của bảng ở TCVN 142-1988 (ISO 3) và được lặp lại trong cột 7 của bảng ở tiêu chuẩn này. Bảng này cũng cho các hiệu số tương ứng đối với các giá trị quy tròn trong các cột 8 đến cột 10.
A.1.2. Mức độ đều đặn của công bội của một dãy số tại một điểm đã cho, được đặc trưng bởi sai lệch, biểu thị bằng phần trăm, giữa công bội thực tại điểm này (hệ thức giữa hai số hạng liền kề) và công bội lý thuyết [6]).
Các sai lệch này, và vì thế cả mức độ đều đặn của công bội giữa hai số hạng liền kề, có thể được xác định bằng phép trừ đại số đơn giản của các hiệu số cho trong các cột 7 đến cột 10 của bảng, bỏ qua các giá trị vô cùng bé[7]).
Độ không đều đặn lớn nhất của công bội tại các điểm khác nhau trong mỗi dãy số R, R’, R’’ được cho dưới chân các cột 1 đến cột 4 của bảng.
A.2. Sai lệch cho phép
A.2.1. Nếu chỉ quan tâm đến điều kiện mà một giá trị quy tròn phải duy trì gần với giá trị lý thuyết tương ứng hơn là các giá trị thuyết liền kề thì điều kiện này được biểu thị bằng một sai lệch lớn nhất cho phép (nếu công bội ![]() không quá lớn) xấp xỉ bằng với
không quá lớn) xấp xỉ bằng với ![]()
A.2.2. Tuy nhiên, tại giới hạn này, hệ thức giữa hai số liên tiếp có thể gần bằng 1 (hoặc 2 lần công bội), điều này là không cho phép đối với độ đều đặn của dãy số.
A.3. Sai lệch thực của các giá trị tính toán
Trong TCVN 142: 1988, các giá trị tính toán được cho trong cột 7 của bảng đến 5 con số có nghĩa tương ứng với sai lệch lớn nhất không vượt quá 0,00005 về giá trị tuyệt đối và tương ứng với sai lệch tương đối 0,0048 % so với giá trị lý thuyết.
A.4. Sai lệch thực của các số ưu tiên
A.4.1. Trong TCVN 142: 1988, các số ưu tiên được cho đến 3 con số có nghĩa và độ chênh lệch tương đối giữa chúng và các giá trị tính toán được nêu trong cột 8.
A.4.2. Độ chênh lệch tương đối này không vượt quá 1,26 % trong khi sai số tuyệt đối đôi khi lại lớn hơn; nhưng cần chú ý rằng các số qui tròn theo quy ước đã được lựa chọn theo cách sao cho độ đều đặn của dãy số, nghĩa là quan hệ giữa hai số hạng, được duy trì rất gần với công bội lý thuyết (độ không đều đặn lớn nhất 1,15 % trong dãy R 40).
A.5. Sai lệch thực của các giá trị quy tròn
A.5.1. Chỉ sử dụng và chỉ trong các trường hợp ngoại lệ các giá trị quy tròn được đưa vào công thức tính toán để đạt được giá trị với hai con số có nghĩa hoặc ngay cả chỉ một con số có nghĩa và duy trì được độ chính xác cho phép và độ đều đặn trong các dãy số R’ và R’’ của các giá trị quy tròn này.[8])
A.5.2 Tuy nhiên, các chênh lệch giữa các giá trị quy tròn với các giá trị lý thuyết lớn hơn nhiều so với các chênh lệch giữa bản thân các số ưu tiên với các giá trị lý thuyết (xem các cột 7 đến 10 – các chênh lệch lớn nhất được đóng khung). Độ đều đặn của công bội các dãy số R’ và R’’ cũng kém hơn so với các dãy số ưu tiên; ví dụ: trong dãy R’’5, độ không đều đặn lớn nhất (xem dưới chân các cột 1 đến cột 4 của bảng) đạt tới 5,37 % so với 1,42 % trong dãy R 5, trong khi trong dãy R’40, độ không đều đặn này đạt tới 2,94 % so với 1,15 % trong dãy R 40.
A.5.3. Cần chú ý rằng đối với một số số hạng việc quy tròn cho phép trong dãy R’’5 hoặc R’’10 lại không cho phép đối với các dãy xít hơn. Vì thế, giá trị 1,5 khác giá trị lý thuyết 5,36 %, gây ra sai lệch 5,60 % đối với công bội giữa giá trị này và số hạng kế tiếp 2,0, một sai lệch cho phép trong dãy R’’10, có công bội ở lân cận 1,25 và sai lệch cho phép lớn nhất 12,9 % theo điều A.2.1. Nhưng giá trị này lại không thể dùng được trong dãy số R’’20 có công bội ở lân cận 1,12 vì sẽ dẫn đến sai lệch 6,58 % đối với số hạng kế tiếp 1,8, và sai lệch lớn nhất cho phép là 6,1 %.
[1] ngoài ra trong một số trường hợp, có thể sử dụng các số hạng có đặc tính cộng được, việc sử dụng ngoại lệ, các giá trị quy tròn như các giá trị của dãy số R”, để giải quyết vấn đề đã nêu trong phạm vi rất hạn hẹp, ví dụ
|
3 + 4 = 7 |
3 + 5 = 8 |
3 + 6 = 9 |
3 + 7 = 10 |
|
3,5 + 4,5 = 8 |
7 + 7 =14 |
v.v… |
|
[2] Việc sử dụng các giá trị ngoại lệ không phải là các số ưu tiên hoặc các giá trị quy tròn – Vì mục đích tiện cận với các tiêu chuẩn hiện hành không được xây dựng phù hợp với các số ưu tiên và chưa được soát xét lại hoặc để duy trì, không thay đổi các quá trình sản xuất vì lý do đảm bảo tính đổi lẫn hoặc để sử dụng các dụng cụ gia công và dụng cụ kiểm tra – sẽ gây khó khăn cho việc tiêu chuẩn hóa trong tương lai cả ở phạm vi quốc gia và quốc tế, và cản trở việc chế tạo hàng loạt các máy móc được phân bậc theo cấp số nhân.
Vì hầu hết các ấn phẩm ISO dựa trên cơ sở số ưu tiên, các tiêu chuẩn quốc gia được xây dựng trước đây cũng sử dụng các số ưu tiên sẽ tự động phù hợp với các tiêu chuẩn ISO, nhưng sẽ khó khăn hơn khi tiện cận những tiêu chuẩn bao gồm các giá trị quy tròn hoặc các giá trị không có liên quan với số ưu tiên.
Sự đưa vào các tiêu chuẩn dãy các giá trị hiện có không thể sửa đổi được, như các hằng số vật lý, không được coi là sự ứng dụng các số ưu tiên, dẫu rằng các giá trị này gần với các số ưu tiên hoặc các giá trị quy tròn; các dãy số này không thể có tất cả các tính chất của số ưu tiên và việc sử dụng chúng có thể tạo ra các khó khăn, đặc biệt là trong tính toán như các tính toán giới thiệu trong 3.4. Các ứng dụng tương tự cho dãy các giá trị hiện có khó mà biến đổi được hiện nay là các mô đun bánh răng.
[3] Xem chú thích cuối trang 1), trang 6.
[4] Xem chú thích cuối trang 2), trang 7.
[5] Ví dụ đối với ưu tiên 8,5, khi bỏ qua sai lệch giữa giá trị tính toán và giá trị lý thuyết, mức độ chính xác là
100 x = 1,02%
[6] Ví dụ đối với dãy số R40, lấy các số hạng 1,60 và 1,70, sai lệch này là
[7] Ví dụ: các số hạng 1,60 và 1,70 cho gần đúng
= 1,059 3 = 1,059 3 (1 + 0,0031)
hệ thức chính xác là 1,0625, sai lệch chính xác là 0,00325 hoặc 0,3 % gần với 2/10000 (trong trường hợp này).
[8] Giá trị 1,2 thay cho 1,18 trong dãy R’40 gây ra sai lệch so với giá trị lý thuyết +0,97 %, và nó cũng được chấp nhận như 1,18, giá trị gây ra sai lệch -0,71 %; nhưng nếu quan tâm đến sự phân bậc thì giá trị 1,2 không khớp đúng vị trí giữa 1,1 và 1,25; trên thực tế, sai lệch so với công bội lý thuyết 1,0593, thu được từ hiệu đại số của các sai lệch trong các cột 7 và cột 8 như đã chỉ dẫn trong A.1.2, là sai lệch đã thay đổi
giữa 1,2 và 1,1 bởi
giữa 1,25 và 1,2 bởi
hai công bội liên tiếp là 1,0866 và 1,0425 thay cho 1,0953.


