Tiêu chuẩn Việt Nam TCVN9435:2012

TIÊU CHUẨN QUỐC GIA

TCVN 9435:2012

ĐIỀU TRA, ĐÁNH GIÁ VÀ THĂM DÒ KHOÁNG SẢN – LIÊN KẾT, HIỆU CHỈNH TÀI LIỆU TỪ

Investigation, evaluation and exploration of minerals – Correction, connection of magnetic prospecting data

Lời nói đầu

TCVN 9435:2012 – Liên kết, hiệu chỉnh tài liệu từ-do Tổng Cục Địa chất và Khoáng sản biên soạn, Bộ Tài nguyên và Môi trường đề nghị, Tổng Cục Tiêu chuẩn Đo lường Chất lượng thẩm định, Bộ Khoa học và Công nghệ công bố.

 

ĐIỀU TRA, ĐÁNH GIÁ VÀ THĂM DÒ KHOÁNG SẢN – LIÊN KẾT, HIỆU CHỈNH TÀI LIỆU TỪ

Investigation, evaluation and exploration of minerals – Correction, connection of magnetic prospecting data

1. Nguyên tắc của phương pháp

Phương pháp hiệu chỉnh và liên kết tài liệu từ là thực hiện các phép hiệu chỉnh nào đó để loại các yếu tố không liên quan đến đối tượng nghiên cứu lên kết quả đo, đồng thời giảm thiểu và loại bỏ các sai số hệ thống tích lũy trong quá trình đo đạc dựa vào việc liên kết số liệu đo ghi với mạng lưới các điểm chuẩn, đánh giá độ chính xác đo ghi tài liệu từ.

2. Phạm vi áp dụng

Tiêu chuẩn phương pháp hiệu chỉnh và liên kết tài liệu từ quy định các bước, phương pháp tính toán, hiệu chỉnh và liên kết tài liệu từ trong phương pháp khảo sát trường từ bằng các từ kế proton hay lượng tử đang được sử dụng ở Việt Nam phục vụ cho công tác điều tra địa chất và tìm kiếm khoáng sản.

3. Định nghĩa và các thuật ngữ

3.1. Trường từ toàn phần (Total Magnetic Field -TMF) của Trái đất là đại lượng vectơ, ký hiệu T hay F.

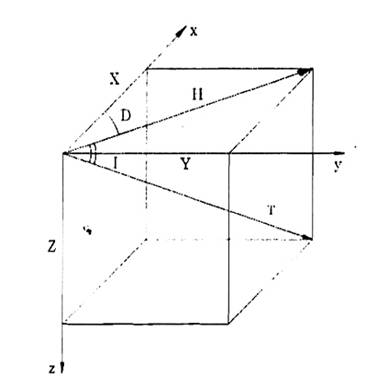
Hình 1: Các thành phần trường điện từ

3.2. Thành phần nằm ngang H (Horizontal Component) là hình chiếu của T lên mặt phẳng nằm ngang.

3.3. Thành phần thẳng đứng Z (Vertical component) là hình chiếu của T trên trục z.

3.4. Độ từ thiên D (declination): là góc giữa H và trục x, D dương khi vectơ T ở phía đông.

3.5. Độ từ khuynh I (inclination): là góc nghiêng giữa T với mặt phẳng nằm ngang, I dương khi vectơ T ở dưới mặt phẳng nằm ngang.

3.6. Các đại lượng trên không cố định theo thời gian mà thay đổi từ ngày này sang ngày khác, từ năm này sang năm khác. Người ta thấy các biến đổi này có tính chất tuần hoàn nhưng chu kỳ, pha, biên độ thay đổi rất khác nhau.

3.7. Đo biến thiên từ là phương pháp đo liên tục giá trị trường từ tại một địa điểm cố định đã được lựa chọn thỏa mãn các điều kiện về kỹ thuật. Các giá trị trường từ đo được tại điểm đo biến thiên được sử dụng để hiệu chỉnh biến thiên từ trong công tác khảo sát từ trường hoặc sử dụng để nghiên cứu các đặc điểm trường địa từ phục vụ công tác điều tra địa chất.

3.8. Tuyến kiểm tra, điểm kiểm tra: Là đoạn tuyến hay điểm có đặc điểm trường từ bình ổn, nằm trong hoặc gần khu vực khảo sát dùng để đo kiểm tra các máy trước và sau mỗi ca đo khảo sát trường từ.

3.9. Mạng lưới tuyến chuẩn (tuyến tựa): Là mạng lưới tuyến song song vuông góc với mạng lưới tuyến khảo sát hay mạng lưới tuyến đa giác được đo để tiến hành liên kết tài liệu từ, giảm thiểu các sai số tích lũy hệ thống trong quá trình đo đạc.

3.10. Niên đại bản đồ từ: Năm lấy làm chuẩn để thành lập bản đồ từ.

3.11. Trường từ bình thường là một khái niệm quy ước. Giá trị đo ghi trường từ tại bất kỳ một điểm nào đó là giá trị tổng gộp, trong đó bao gồm trường địa từ chính hay còn gọi là trường bình thường, phần trường từ biến thiên nhanh chu kỳ ngắn và các dị thường liên quan đến các cấu tạo địa chất khu vực và địa phương. Để nghiên cứu và giải quyết các nhiệm vụ địa chất, trong phương pháp từ, trường bình thường là trường để so với nó ta có thể xác định dị thường từ các cấu tạo địa chất, thành tạo địa chất gây nên.

3.12. Dị thường từ: Là giá trị trường từ sau khi đã hiệu chỉnh trường bình thường.

3.13. Nano Tesla: Đơn vị đo cường độ từ trường trong hệ đơn vị quốc tế SI. 1nT = 1.10^-9T.

1Tesla = 10⁴ estet = (1/4Õ) 10⁷ Ampe/met

3.14. Gama: Đơn vị đo cường độ từ trường trong hệ đơn vị quốc tế CGSM

1gama = 10^-5 estet = 10^-9 tesla

Vậy 1gama = 1 nanotesla (nT)

3.15. Ca đo khảo sát trường từ: Khoảng thời gian thực hiện lộ trình khảo sát trường từ, tính từ lúc đo điểm kiểm tra lượt đi đến khi kết thúc đo điểm kiểm tra lượt về.

3.16. Thời gian thực GPS: Thời gian chuẩn quốc tế từ hệ thống định vị GPS.

4. Phương pháp hiệu chỉnh và liên kết tài liệu từ

4.1. Trình tự hiệu chỉnh và liên kết tài liệu từ

4.1.1. Khi đo khảo sát trường từ theo diện, thành lập bản đồ trường các loại quy định xử lý tài liệu từ gồm các bước sau đây:

4.1.1.1. Kiểm tra sơ bộ tài liệu từ.

4.1.1.2. Gắn tọa độ cho tài liệu từ

4.1.1.3. Hiệu chỉnh biến thiên từ

4.1.1.4. Liên kết mạng lưới điểm chuẩn, tuyến chuẩn

4.1.1.5. Liên kết các giá trị điểm thường với các giá trị điểm chuẩn.

4.1.1.6. Hiệu chỉnh trường bình thường (tính dị thường từ)

4.1.1.7. Tính toán sai số đo đạc.

4.1.1.8. Thành lập các bản đồ trường từ theo yêu cầu của đề án.

4.1.2. Khi đo khảo sát trường từ theo tuyến, quy định xử lý tài liệu từ gồm các bước sau đây:

4.1.2.1. Kiểm tra sơ bộ tài liệu từ.

4.1.2.2. Gắn tọa độ cho tài liệu từ

4.1.2.3. Hiệu chỉnh biến thiên từ

4.1.2.4. Hiệu chỉnh ảnh hưởng trường từ cảm ứng từ các phương tiện (nếu có) thực hiện công tác đo từ lên kết quả.

4.1.2.5. Hiệu chỉnh trường bình thường (tính dị thường từ)

4.1.2.6. Tính toán sai số đo đạc

4.1.2.7. Thành lập các bản đồ tuyển khảo sát trường từ theo yêu cầu của đề án

4.2. Kiểm tra sơ bộ tài liệu từ, gắn tọa độ

4.2.1. Đối với số liệu ghi chép bằng sổ sách: Hoàn chỉnh các ghi chép ở sổ ghi (hoàn chỉnh các vấn đề chi chép còn thiếu) nhưng không được sửa chữa số liệu đo đạc thực địa.

4.2.2. Đối với số liệu ghi tự động bằng máy ghi, tiến hành trút số liệu vào máy tính, kiểm tra sơ bộ hình dạng đường cong trường từ nhằm phát hiện nhiễu, ghi chú để lưu ý trong quá trình xử lý sau này.

4.2.3. Gắn tọa độ địa lý hay số thứ tự các điểm đo cho tài liệu từ, để sử dụng sau cho việc vẽ bản đồ trường từ hay đồ thị tuyến đo từ.

4.3. Hiệu chỉnh biến thiên từ

4.3.1. Công thức tính hiệu chỉnh biến thiên từ

Hiệu chỉnh biến thiên từ tại thời điểm đo nào đó tính theo công thức:

T = T_đo – dT_bt – dT_bttk (4.1)

Trong đó:

+ T: Giá trị trường từ toàn phần được hiệu chỉnh biến thiên quy về năm thành lập bản đồ.

+ T­_đo: Giá trị trường từ toàn phần đo được tức thời tại điểm đo trong vùng khảo sát.

+ dT_bt: Giá trị biến thiên của trường từ tại điểm đo trong vùng ở thời điểm khảo sát.

+ dT_bttk: Đại lượng biến thiên thế kỷ, trong phạm vi vùng khảo sát không lớn, giá trị này coi như một hằng số. dT_bttk tính được từ các bản đồ trường bình thường.

4.3.2. Công thức tính giá trị biến thiên từ dT_bt

Giả sử biến thiên từ trong toàn vùng khảo sát là đồng nhất, bằng giá trị biến thiên tại điểm đặt máy đo biến thiên từ. Đại lượng biến thiên từ tại dT_bt được tính như sau:

dT_bt = T_đbt – T_tbn (4.2)

– T_đbt: Giá trị trường từ đo tại điểm đo biến thiên.

– T_tbn: Giá trị trường trung bình năm tại điểm đo biến thiên, là giá trị tính trung bình cho cả năm tại điểm đo biến thiên. Thực tế, không thể đo biến thiên cả năm liên tục suốt ngày đêm tại điểm đo biến thiên.

4.3.3. Cách tính gần đúng giá trị trung bình năm T_tbn:

4.3.3.1. Nếu khu vực khảo sát trong phạm vi sử dụng giá trị đo biến thiên của đài địa từ và sử dụng số liệu đo biến thiên của đài để hiệu chỉnh biến thiên từ thì phải sử dụng giá trị trung bình năm của đài.

4.3.3.2. Nếu không sử dụng số liệu biến thiên từ của đài địa từ, phải sử dụng số liệu đo biến thiên từ trong khoảng thời gian nhiều hơn 4 tháng và kết quả đo ghi biến thiên từ liên tục 3 ngày đêm (72h liên tục) để tính gần đúng giá trị T_tbn của điểm đo biến thiên.

4.3.3.2.1. Đo biến thiên từ liên tục 3 ngày 3 đêm (72h liên tục).

4.3.3.2.2. Tính độ chênh lệch trung bình ngày – đêm (DT_ng-đ).

DT_ng-đ­ = T_tbng – T_tb3ng-đ        (4.3)

Trong đó:

– T_tb3ng-đ: Giá trị trường từ trung bình 3 ngày đêm (72 giờ) tại điểm đo biến thiên.

– T_tbng: Giá trị trường từ trung bình 3 ngày (6h sáng đến 6h tối) tại điểm đo biến thiên.

4.3.3.2.3. Tính gần đúng giá trị trường trung bình năm tại điểm đo biến thiên như sau T_tbn:

T_tbn = T_tbđ – DT_ng-đ (4.4)

– T_tbđ: Trung bình các giá trị đo tại điểm biến thiên.

Các giá trị đo tại điểm biến thiên trong khoảng tháng 4,5,6,7,8 sẽ gần với giá trị trung bình năm nhất.

4.3.3.3. Đối với đo từ theo tuyến lộ trình địa chất, không thành lập bản đồ trường từ lấy giá trị T_tbn là giá trị trung bình tại điểm đo biến thiên trong suốt thời gian thi công.

4.3.3.4. Đối với đo từ độ chính xác cao, trên diện tích nhỏ lấy giá trị T_tbn là giá trị trung bình tại điểm đo biến thiên trong suốt thời gian thi công.

4.3.4. Cách tính đại lượng biến thiên thế kỷ dT_bttk:

4.3.4.1. Trong phạm vi vùng khảo sát không lớn, giá trị này coi như một hằng số. dT_bttk tính được từ các bản đồ trường bình thường.

4.3.4.2. Nếu công tác đo đạc trường từ tiến hành nhiều hơn 1 năm thì phải sử dụng hệ số biến thiên thế kỷ để đưa về giá trị niên đại thành lập bản đồ.

4.3.4.3. Cách tính dT_bttk: hệ số biến thiên thế kỷ dT_bttk được tính trung bình hiệu các giá trị trường bình thường của các năm tại cùng các nút tọa độ.

4.4. Hiệu chỉnh ảnh hưởng trường từ cảm ứng từ các phương tiện thực hiện công tác đo từ lên kết quả.

4.4.1. Khi đo từ trường bằng phương pháp đo ôtô đường bộ, cần thiết phải hiệu chỉnh giá trị trường cảm ứng của ôtô lên kết quả đo.

4.4.2. Giá trị hiệu chỉnh ảnh hưởng trường cảm ứng được tính cho các hướng: 0⁰, 45⁰, 90⁰, 135⁰, 180⁰, 225⁰, 270⁰, 315⁰.

4.4.3. Tùy theo hướng của phương tiện khi di chuyển mà hiệu chỉnh giá trị phù hợp.

4.5. Cân bằng mạng lưới tuyến chuẩn (tuyến tựa)

4.5.1. Quy định chung

4.5.1.1. Sau khi đo xác định trường tại các điểm chuẩn thì các giá trị này phải được liên kết với nhau và công việc này được gọi là cân bằng mạng lưới các điểm chuẩn.

4.5.1.2. Giá trị trường từ sử dụng khi cân bằng mạng lưới tựa là giá trị đã hiệu chỉnh biến thiên từ.

4.5.2. Các phương pháp cân bằng mạng lưới tuyến chuẩn:

Có nhiều cách cân bằng mạng lưới các điểm chuẩn. Sau đây là các phương pháp chủ yếu:

4.5.2.1. Cân bằng mạng lưới đa giác theo phương pháp giải phương trình (cách này ứng dụng cho mạng lưới chuẩn độc lập).

4.5.2.1.1. Trong một hệ các đa giác khép kín, mỗi cạnh có trọng số khác nhau phụ thuộc vào độ chính xác của giá trị gia số trường của cạnh đó. Khi việc đo có độ chính xác như nhau, ảnh hưởng nhiễu như nhau thì trọng số lúc này phụ thuộc độ dài của cạnh, nó tỷ lệ nghịch với độ dài cạnh.

4.5.2.1.2. Gia số trường của cạnh nối hai điểm i và j là D_ij của một đa giác. Quy định theo chiều kim đồng hồ trường từ tăng thì D­_ij > 0, ngược lại D_ij < 0.=”” về=”” lý=”” thuyết=”” tổng=”” gia=”” số=”” của=”” đa=”” giác=”” kép=”” kín=”” phải=”” bằng=”” không.=”” do=”” sai=”” số=”” ngẫu=”” nhiên,=”” tổng=”” này=”” có=”” giá=”” trị=”” bằng=””>_i.

Hình 2 Sơ đồ cân bằng theo phương pháp giải phương trình

4.5.2.1.3. Độ dài giữa các điểm của 1 cạnh ký hiệu là a^l_i-j, (a là độ dài cạnh, I là số hiệu của đa giác: i, j l là tên các điểm chuẩn.

4.5.2.1.4. Gọi k_n là hệ số điều chỉnh cho mỗi đơn vị độ dài các cạnh của mỗi đa giác thứ n. Lúc này ta có hệ phương trình sau:

(a^I_1-2 + a^I_2-3 + a^I_3-4 + a^I-II_4-1) k_I – a^I-II_1-4 k_II + v₁ = 0

(a^I-II_1-4 + a^II_4-5 + a^II-III_5-8 + a^II_8-1) k_II – a^I-II_4-1 k₁ -a^II-III_8-5 k_III + v_II = 0 (4.5)

(a^II-III_8-5 + a^III_5-6 + a^III_6-7 + a^III_7-8) k^III – a^II-III_15-8 k_II + v_III = 0

Số phương trình bằng số đa giác.

Giải hệ phương trình ta sẽ được các giá trị k_n.

4.5.2.1.5. Giá trị hiệu chỉnh cho các cạnh cụ thể sẽ là

d^I_1-2 = a^I_1-2 k₁

d^I_2-3 = a^I_2-3 k₁ (4.6)

d^I_3-4 = a^I_3-4 k₁

d^I-II_4-1 = a^I-II_4-1 (k_I – k_II)

4.5.2.1.6. Sau khi có các giá trị d_i-j ta tính gia số các cạnh bằng D_ij + d_ij.

4.5.2.1.7. Sai số mạng lưới tựa tính theo công thức:

m =   (4.7)

K là số cạnh (trên Hình 2, k = 10)

R số đa giác (trên Hình 2, r=3).

4.5.2.2. Cân bằng mạng lưới đa giác theo phương pháp Popop (Hình 3).

4.5.2.2.1. Tính độ chênh trong các đa giác. Trong một đa giác giá trị tăng lên của trường giữa các điểm theo chiều kim đồng hồ được quy ước là dương. Giá trị tăng của trường giữa các điểm ngược chiều kim đồng hồ được quy ước là âm. Trong trường hợp này mũi tên sẽ ngược với chiều kim đồng hồ. Tổng gia số các cạnh được ghi vào trung tâm của mỗi đa giác.

4.5.2.2.2. Tính trọng số các cạnh của đa giác (số đỏ). Sai số khép phân cho mỗi cạnh tỷ lệ ngược với độ chính xác đo đạc. Thông thường trong một mạng lưới tựa số lần xác định gia số mỗi cạnh đều bằng nhau nên trọng số tỷ lệ thuận với thời gian đo (khoảng cách) mỗi cạnh là chủ yếu.

4.5.2.2.3. Tiến hành cân bằng có thể bắt đầu từ một đa giác nào đó có sai số khép lớn nhất và nằm ở phần giữa của mạng lưới tựa.

4.5.2.2.4. Chuyển sang đa giác thứ liền kề. Với cạnh chung, khi chuyển sang sai số của đa giác bên cạnh phải đổi dấu. Sai số khép của đa giác này sẽ là tổng sai số khép ban đầu cộng với sai số khép vừa tính cho cạnh chung của đa giác liền kề. Trong trường hợp phân phối sai số khép còn dư, số dư này phân cho cạnh dài hơn hoặc cạnh nằm phía ngoài.

4.5.2.2.5. Song lượt phân bố thứ nhất, tính lại tổng sai số khép của các đa giác rồi chuyển sang lượt phân bố thứ II và lại được bắt đầu từ đa giác có sai số khép lớn nhất. Cứ như vậy cho đến khi sai số khép của các đa giác bằng không.

Hình 3: Sơ đồ cân bằng theo phương pháp Popop

4.5.2.3. Cân bằng mạng lưới tuyến song song vuông góc với tuyến khảo sát

Giả sử ta có mạng lưới tuyến chuẩn vuông góc với tuyến thường, I, II, III, IV và V như hình vẽ dưới đây:

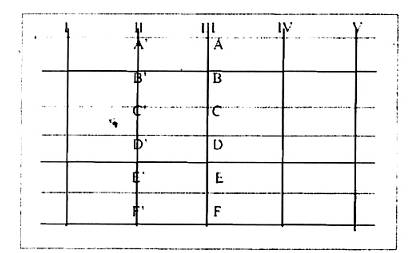
Hình 4 : Sơ đồ mạng lưới tuyến trục vuông góc với tuyến thường

4.5.2.3.1. Ta chọn tuyến chuẩn III làm tuyến chuẩn gốc, các tuyến chuẩn khác được liên kết về tuyến chuẩn III. Tuyến chuẩn gốc được chọn sao cho các giá trị đo trên tuyến chuẩn gốc đạt độ chính xác cho phép tốt nhất.

4.5.2.3.2. Ta tiến hành chuẩn tuyến chuẩn II về tuyến chuẩn III như sau: Giả sử có 2 tuyến trục III và II. Trên đó có các điểm chuẩn A, B, C, D, G, E, F (tuyến trục III) và A’, B’, C’, D’, G’, E’, F’ (tuyến trục II). Các cặp điểm này có các tuyến thường cắt qua.

4.5.2.3.3. Xác định giá trị trung bình thường (T, Z…) trên các điểm chuẩn này. Thí dụ với các điểm chuẩn trên các điểm chuẩn tuyến III và II lần lượt có giá trị là 55, 60, 48, 40, 82, 65, 51 và 92, 98, 76, 71, 116, 96, 79.

Lúc này có thể xác định được giá trị trường từ chênh giữa các cặp điểm chuẩn có 1 tuyến thường cắt qua

A’A = 92 – 55 = 37 = D_A

B’B = 98 – 60 = 38 = D_B

C’C = 76 – 48 = 28 = D_C

D’D = 71 – 40 = 31 = D_D (4.8)

G’G = 116 – 82 = 34 = D_G

E’E = 96 – 65 = 31= D_E

F’F = 79 – 51 = 29 = D_F

Giá trị i gồm sự chênh lệch từ trường của cặp điểm chuẩn I và cả sự chưa thống nhất trong mạng lưới chuẩn đo ở các điều kiện khác nhau.

Khi đo tuyến thường qua AA’, BB’, …, FF’ sẽ xác định được gia số trường từ giữa các cặp điểm chuẩn i. Do đó một tuyến thường trong cùng một điều kiện nên khi đo qua hai điểm chuẩn tương ứng trên hai tuyến trục sẽ không còn sự chênh lệch do sự không đồng nhất.

4.5.2.3.4. Xác định được giá trị chênh lệch là:

L_i = D_I – d_I  (4.9)

4.5.2.3.5. Giá trị chênh chung của các điểm chuẩn ở tuyến trục II so với tuyến trục III là:

L_(II-III) =  (4.10)

K là số cặp các điểm chuẩn trên hai tuyến trục

L_(II-III): giá trị hiệu chỉnh các giá trị trường của các điểm trên tuyến trục II về tới tuyến trục III.

Ví dụ: (A, B, …, F tương ứng bằng 12, 15, 4, 6, 11, 7, 4. Lúc này LA, LB, …, LF tương ứng bằng 25, 23, 24, 25, 23, 24, 24, cuối cùng L_­(II-III) = 24

A	B	C	D	G	E	F		III
55	60	48	40	82	65	51	nT

 

92	98	76	71	116	96	79	nT
A’	B’	C’	D’	G’	E’	F’		II
37	38	28	31	34	37	28	Di
12	15	4	6	11	7	4	di
25	23	24	25	23	24	24	Li

Hình 5: Sơ đồ cân bằng theo mạng lưới tuyến trục vuông góc với tuyến thường

4.5.2.3.6. Sau khi chuẩn tuyến II về tuyến III đã hoàn thành, ta lại tiến hành chuẩn tuyến I về tuyến chuẩn II (đã chuẩn về tuyến III). Công việc tiếp tục đối với các cặp tuyến chuẩn tiếp theo.

4.5.2.3.7. Liên kết số liệu tuyến thường với mạng lưới điểm chuẩn

4.5.2.3.7.1. Số liệu tuyến thường liên kết với mạng lưới tuyến chuẩn là số liệu đã hiệu chỉnh biến thiên từ.

4.5.2.3.7.2. Giả sử trong 1 ca đo, lần lượt qua 4 điểm chuẩn là I, II, III, IV và các điểm thường như trong bảng dưới đây:

Số hiệu điểm chuẩn	I						II				III					IV
Số hiệu điểm thường		1	2	3	4	5		6	7	8		9	10	11	12

4.5.2.3.7.3. Hiệu giá trị tại điểm chuẩn của ca đo (thường – chuẩn) như bảng (nT) dưới đây:

Điểm chuẩn

I

II

III

IV

2

8

4

– 2

4.5.2.3.7.4. Giá trị hiệu chỉnh để liên kết các điểm đo thường với các điểm chuẩn sẽ tính theo phương pháp trung bình tuyến tính theo bảng dưới đây:

Số hiệu điểm chuẩn	I						II				III					IV
Số hiệu điểm thường		1	2	3	4	5		6	7	8		9	10	11	12
Giá trị hiệu chỉnh (nT)		-3	-4	-5	-6	-7		-7	-6	-5		-3	-2	-1	+1

4.6. Hiệu chỉnh trường bình thường

Dị thường từ T được tính theo công thức:

DT = T_lk – T₀ (4.11)

Trong đó;

– DT: Dị thường từ

– T_lk: Giá trị trường từ sau khi đã liên kết với mạng lưới điểm chuẩn.

– T₀: Trường từ bình thường cùng niên đại.

4.7. Đánh giá chất lượng tài liệu, tính toán sai số đo đạc

4.7.1. Quy định chung: Chất lượng công tác đo từ mặt đất được đánh giá theo các mặt sau:

– Sai số đo tính theo các tài liệu đo kiểm tra lặp của các điểm đo thường, so sánh tài liệu đo hai máy song song.

– Sai số tổng cộng của việc khảo sát.

– Mức độ đúng đắn của việc ghi chép, chỉnh lý và thành lập tài liệu thực địa so với yêu cầu của quy phạm kỹ thuật và của phương án.

– Chất lượng xử lý các tài liệu thực địa và ở giai đoạn tổng kết:

+ Chất lượng các tài liệu bản vẽ báo cáo;

+ Mức độ giải quyết các nhiệm vụ đặt ra trong phương án và hiệu quả địa chất của khảo sát từ
4.7.2. Tính sai số đo đạc: Sai số đo đạc tính theo các đại lượng sau:

+ Sai số bình phương trung bình trên mỗi điểm chuẩn trong mạng lưới chuẩn s_m.

+ Sai số bình phương trung bình của cả mạng lưới chuẩn s_c.

+ Sai số bình phương trung bình của mạng lưới điểm quan sát trên tuyến thường, s_th.

Sai số s_c và s_th phải thỏa mãn bất đẳng thức

s_c <>s_th £ (2 ¸ 2,5)s_c (4.12)

Sai số chung của tài liệu đo đạc tính theo công thức

s = ± (4.13)

+ Sai số bình phương trung bình ở mỗi điểm chuẩn

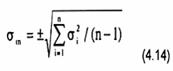
Ở đây i là hiệu giá trị đo lần thứ i tại điểm chuẩn hay điểm kiểm tra với giá trị trung bình của n lần đo trên điểm chuẩn đó:

+ Sai số bình phương trung bình của mạng lưới chuẩn xác định như sau:

– Khi mạng lưới chuẩn được cân bằng theo phương pháp Popôp

Trong đó:

i là hiệu hai giá trị trường từ của mỗi cạnh đa giác thứ i trước và sau khi cân bằng.

P_i là trọng số của cạnh thứ i.

n là số cạnh của mạng lưới chuẩn.

r là số đa giác khép kín.

+ Khi mạng lưới chuẩn liên kết theo phương pháp điểm nút:

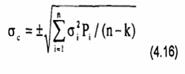
Ký hiệu như trên

n số các khâu giữa hai điểm chuẩn

k là số các điểm chuẩn.

P_i  được xác định tỷ lệ thuận với số lần quan trắc trên cạnh và tỷ lệ nghịch với độ dài của cạnh (thời gian đo).

+ Sai số bình phương trung bình của việc đo trên mạng lưới điểm đo thường.

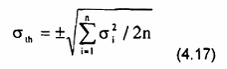
s_i là hiệu giá trị trường tại điểm i đo lần đầu và lần đo kiểm tra.

n là số điểm đo kiểm tra.

 

PHỤ LỤC A

DANH MỤC TÀI LIỆU THAM KHẢO

+ Địa từ và thăm dò từ. NXB Đại học quốc gia Hà Nội 2006, Tôn Tích Ái.

+ Bài giảng phương pháp từ, trường Đại học Mỏ-Địa chất 2000, Bùi Thế Bình.

+ Bài giảng Thăm dò từ và địa từ dùng cho cao học ngành địa vật lý, trường Đại học Mỏ – Địa chất 1999, Tôn Tích Ái.

+ Magnetic Surveys Book: Principles, Practice & Interpretation, 2005, Geosoft.

+ Đề tài khoa học công nghệ cấp bộ ” Nghiên cứu và thành lập bộ chương trình hiệu chỉnh và liên kết tài liệu từ phổ gamma hàng không”, Kiều Trung Thủy, 2007.

 

MỤC LỤC

Lời nói đầu

1. Định nghĩa phương pháp

2. Phạm vi áp dụng

3. Định nghĩa và các thuật ngữ

4. Phương pháp hiệu chỉnh và liên kết tài liệu từ

4.1. Trình tự hiệu chỉnh và liên kết tài liệu từ

4.2. Kiểm tra sơ bộ tài liệu từ, gắn tọa độ

4.3. Hiệu chỉnh biến thiên từ

4.4. Hiệu chỉnh ảnh hưởng trường từ cảm ứng từ các phương tiện thực hiện công tác đo từ lên kết quả

4.5. Cân bằng mạng lưới tuyến chuẩn (tuyến tựa)

4.6. Hiệu chỉnh trường bình thường (tính dị thường từ)

4.7. Đánh giá chất lượng tài liệu, tính toán sai số đo đạc

Phụ lục A Danh mục tài liệu tham khảo