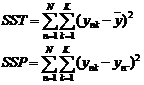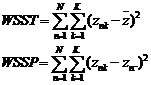Nội dung toàn văn Tiêu chuẩn quốc gia TCVN 9598:2013 về Hiệu chuẩn tuyến tính sử dụng mẫu chuẩn
TIÊU CHUẨN QUỐC GIA
TCVN 9598:2013
ISO 11095:1996
HIỆU CHUẨN TUYẾN TÍNH SỬ DỤNG MẪU CHUẨN
Linear calibration using reference materials
Lời nói đầu
TCVN 9598:2013 hoàn toàn tương đương với ISO 11095:1996;
TCVN 9598:2013 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Lời giới thiệu
Hiệu chuẩn là một phần thiết yếu của hầu hết các thủ tục đo. Đó là một tập hợp các hoạt động để thiết lập quan hệ giữa các giá trị được chỉ ra bởi hệ thống đo và các giá trị được chấp nhận tương ứng của một số “chuẩn” trong những điều kiện quy định. Trong tiêu chuẩn này, các chuẩn là mẫu chuẩn.
Mẫu chuẩn (RM) là một chất hoặc vật mẫu về một hoặc nhiều tính chất được thiết lập phù hợp để xác nhận giá trị của một hệ thống đo. Có nhiều loại RM:
a) mẫu chuẩn nội bộ là RM do người sử dụng xây dựng để sử dụng nội bộ;
b) mẫu chuẩn bên ngoài là RM do người không phải là người sử dụng cung cấp;
c) mẫu chuẩn được chứng nhận là RM do một tổ chức được thừa nhận là có đủ năng lực sản xuất và chứng nhận.
HIỆU CHUẨN TUYẾN TÍNH SỬ DỤNG MẪU CHUẨN
Linear calibration using reference materials
1. Phạm vi áp dụng
Tiêu chuẩn này đưa ra:
a) nguyên tắc chung cần thiết để hiệu chuẩn hệ thống đo và duy trì hệ thống đo “đã hiệu chuẩn” trong trạng thái kiểm soát thống kê;
b) phương pháp cơ bản đối với
– ước lượng hàm hiệu chuẩn tuyến tính với một trong hai giả định liên quan đến độ biến động của phép đo;
– kiểm tra giả định về tuyến tính với một trong hai giả định liên quan đến độ biến động của phép đo, và
– ước lượng giá trị của đại lượng mới chưa biết bằng cách chuyển đổi các giá trị đo thu được trên đại lượng đó với hàm hiệu chuẩn;
c) phương pháp kiểm soát việc sử dụng mở rộng hàm hiệu chuẩn cho việc
– phát hiện khi hàm hiệu chuẩn cần được cập nhật, và
– ước lượng độ không đảm bảo của giá trị đo được sau khi chuyển đổi bằng hàm hiệu chuẩn;
d) hai lựa chọn cho phương pháp cơ bản trong điều kiện đặc biệt;
e) minh họa phương pháp cơ bản và phương pháp kiểm soát bằng ví dụ.
Tiêu chuẩn này áp dụng cho các hệ thống đo có sẵn mẫu chuẩn để sử dụng.
Tiêu chuẩn này áp dụng cho các hệ thống đo với hàm hiệu chuẩn tuyến tính giả định và đề xuất phương pháp kiểm tra giả định về tính tuyến tính. Nếu biết trước hàm hiệu chuẩn là phi tuyến, thì không áp dụng tiêu chuẩn này trừ khi sử dụng “kỹ thuật đóng khung” mô tả ở 8.3.
Tiêu chuẩn này không phân biệt giữa các loại RM khác nhau và coi các giá trị chấp nhận của RM được chọn để hiệu chuẩn hệ thống đo là không có sai số.
2. Tài liệu viện dẫn
Các tài liệu viện dẫn dưới đây rất cần thiết cho việc áp dụng tiêu chuẩn này. Đối với các tài liệu ghi năm công bố thì áp dụng bản được nêu. Đối với các tài liệu không ghi năm công bố thì áp dụng bản mới nhất, bao gồm cả các sửa đổi.
TCVN 8890:2011 (ISO Guide 30:1992), Thuật ngữ và định nghĩa sử dụng cho mẫu chuẩn.
ISO 3534-1:1993 1), Statistics – Vocabulary and symbols – Part 1: Probability and general statistical term (Thống kê học – Từ vựng và ký hiệu – Phần 1: Thuật ngữ chung về thống kê và xác suất)
ISO 3534-2:1992 2), Statistics – Vocabulary and symbols – Part 2: Statistical quality control (Thống kê học – Từ vựng và ký hiệu – Phần 2: Kiểm soát chất lượng thống kê)
3. Thuật ngữ và định nghĩa
Tiêu chuẩn này áp dụng các thuật ngữ và định nghĩa trong TCVN 8244-1 (ISO 3534-1), TCVN 8244-2 (ISO 3534-2) và các thuật ngữ, định nghĩa dưới đây.
3.1.
Mẫu chuẩn (reference material)
Chất hoặc vật mẫu về một hay nhiều tính chất được thiết lập phù hợp để sử dụng cho việc xác nhận giá trị sử dụng của một hệ thống đo.
4. Nguyên tắc chung
Hiệu chuẩn là một quy trình xác định sự khác biệt mang tính hệ thống có thể có giữa một hệ thống đo và hệ thống “quy chiếu” đại diện bởi mẫu chuẩn và các giá trị chấp nhận của chúng. Trong tiêu chuẩn này, thuật ngữ hệ thống (hệ thống đo hay hệ thống quy chiếu) được dùng để nói đến không chỉ phương tiện đo mà cả tập hợp các quy trình, người vận hành và điều kiện môi trường kèm theo phương tiện đó.
Đầu ra của quy trình tiêu chuẩn là hàm hiệu chuẩn được dùng để chuyển đổi các kết quả đo sau này. Trong tiêu chuẩn này, thuật ngữ “chuyển đổi” đề cập đến
– việc hiệu chính các phép đo sau này nếu cả giá trị chấp nhận của mẫu chuẩn (RM) và các giá trị quan trắc có cùng một đơn vị; hoặc
– chuyển đổi từ đơn vị của phép đo quan trắc thành đơn vị của RM.
Giá trị sử dụng của hàm hiệu chuẩn phụ thuộc vào hai điều kiện:
a) các phép đo mà từ đó hàm hiệu chuẩn được tính là đại diện cho điều kiện chuẩn trong đó hệ thống đo hoạt động; và
b) hệ thống đo ở trạng thái được kiểm soát.
Thực nghiệm hiệu chuẩn phải được thiết kế để đảm bảo đáp ứng điểm a). Phương pháp kiểm soát xác định, càng sớm càng tốt, khi hệ thống được coi là ngoài tầm kiểm soát.
Quy trình nêu trong tiêu chuẩn này chỉ áp dụng cho các hệ thống đo có quan hệ tuyến tính với hệ thống quy chiếu của chúng. Để kiểm tra giả định về tuyến tính có đúng hay không, phải sử dụng từ hai mẫu chuẩn trở lên trong quá trình thực nghiệm hiệu chuẩn. Điều này được minh họa trong phương pháp cơ bản. Bằng việc sử dụng nhiều RM, phương pháp cơ bản cung cấp chiến lược và kỹ thuật để phân tích dữ liệu thu thập được trong quá trình thực nghiệm hiệu chuẩn. Nếu tính tuyến tính đã rõ thì có thể sử dụng phương pháp thay thế, đơn giản hơn phương pháp cơ bản để ước lượng hàm hiệu chuẩn tuyến tính dựa trên một điểm. Phương pháp “hiệu chuẩn một điểm” này (tiếp theo chuyển đổi cấp “không”) không cho phép đối với bất kỳ kiểm nghiệm giả thuyết nào, nhưng đây là một phương pháp nhanh và dễ dàng để “hiệu chuẩn lại” một hệ thống đã được nghiên cứu kỹ lưỡng hơn trong các thực nghiệm trước đó. Nếu có nghi vấn về tuyến tính thì có thể sử dụng lựa chọn thứ hai, gọi là “phương pháp đóng khung”.
Phương pháp cơ bản và phương pháp một điểm dựa trên giả định rằng nỗ lực hiệu chuẩn sẽ có hiệu lực trong khoảng thời gian ổn định của quá trình. Để nghiên cứu về khoảng thời gian hiệu chuẩn có hiệu lực, cần phải có phương pháp kiểm soát. Phương pháp kiểm soát được thiết kế để phát hiện có thay đổi diễn ra trong hệ thống hay không để làm cơ sở cho việc điều tra và/hoặc hiệu chuẩn lại. Phương pháp kiểm soát cũng cung cấp một cách thức đơn giản để xác định độ chụm của các giá trị đã được chuyển đổi bằng hàm hiệu chuẩn đã cho.
Phương pháp đóng khung tốn công sức nhưng có thể cho độ chính xác cao hơn trong việc xác định giá trị của đại lượng chưa biết. Phương pháp này sử dụng hai RM có giá trị càng gần càng tốt (đóng khung) đối với mỗi đại lượng chưa biết và suy ra giá trị chuyển đổi của đại lượng chưa biết từ các phép đo đại lượng chưa biết cũng như các giá trị của hai RM. Chỉ giả định độ ổn định ngắn hạn của quá trình đo (tính ổn định trong quá trình đo đại lượng chưa biết và hai RM). Tính tuyến tính chỉ được giả định trong khoảng giữa các giá trị của hai RM.
5. Phương pháp cơ bản
5.1. Khái quát
Điều này mô tả cách ước lượng và sử dụng hàm hiệu chuẩn tuyến tính khi có sẵn nhiều (hơn hai) RM. Sự sẵn có nhiều RM cho phép kiểm định được tính tuyến tính của hàm hiệu chuẩn.
5.2. Giả định
5.2.1. Giả định rằng không có sai số trong các giá trị chấp nhận của RM (giả định này sẽ không được kiểm tra trong tiêu chuẩn này). Trong thực tế, giá trị chấp nhận của RM được viện dẫn cùng với độ không đảm bảo của chúng. Giả định không có sai số trong giá trị chấp nhận của RM có thể được coi là hợp lệ nếu độ không đảm bảo là nhỏ so với độ lớn của sai số trong giá trị đo được của các RM này (xem tài liệu tham khảo [1]).
CHÚ THÍCH 1: Trong trường hợp RM đã được xử lý hóa học hoặc, trong một số trường hợp là xử lý vật lý, trước khi lấy các số đọc của phương tiện đo, tiêu chuẩn này có thể đánh giá thấp độ không đảm bảo gắn với phép chuyển đổi kết quả đo mới.
5.2.2. Hàm hiệu chuẩn được giả định là tuyến tính (giả định này sẽ được kiểm chứng).
5.2.3. Các phép đo lặp lại của RM cho trước được giả định là độc lập và có phân bố chuẩn với phương sai gọi là “phương sai dư” (giả định về tính độc lập và phân bố chuẩn sẽ không được kiểm chứng trong tiêu chuẩn này). Căn bậc hai của phương sai dư được gọi là độ lệch chuẩn dư.
5.2.4. Độ lệch chuẩn dư được giả định là không đổi hay tỷ lệ thuận với giá trị chấp nhận của RM (giả định này sẽ được kiểm chứng).
5.3. Thực nghiệm hiệu chuẩn
5.3.1. Điều kiện thực nghiệm
Điều kiện thực nghiệm cần giống như điều kiện vận hành bình thường của hệ thống đo; nghĩa là, nếu, ví dụ, có nhiều người vận hành sử dụng thiết bị đo thì cần có nhiều hơn một người vận hành đại diện trong thực nghiệm hiệu chuẩn.
5.3.2. Lựa chọn RM
Dãy giá trị kéo dài bởi các RM được chọn cần bao gồm (trong chừng mực có thể) dãy giá trị gặp phải trong điều kiện vận hành bình thường của hệ thống đo.
Thành phần của RM được chọn cần càng gần với thành phần của vật liệu mục tiêu cần đo càng tốt.
Giá trị của RM cần được phân bố cách đều nhau trong dãy giá trị gặp phải trong điều kiện vận hành bình thường của hệ thống đo.
5.3.3. Số lượng RM, N
Số lượng RM sử dụng để đánh giá hàm hiệu chuẩn ít nhất là 3.
Đối với đánh giá ban đầu hàm hiệu chuẩn, khuyến nghị số lượng nhiều hơn 3 (ít nhất là 3 trong khoảng con bất kỳ có nghi ngờ về tính tuyến tính của hàm hiệu chuẩn).
5.3.4. Số phép lặp, K
Mỗi RM cần được đo ít nhất hai lần (khuyến nghị càng nhiều phép lặp càng tốt). Số lần lặp cần giống nhau đối với tất cả các RM.
Thời gian và điều kiện thực hiện phép lặp cần bao trùm phạm vi rộng cần thiết để đảm bảo rằng tất cả các điều kiện hoạt động đều được đại diện.
5.4. Chiến lược phân tích dữ liệu
5.4.1. Vẽ đồ thị dữ liệu để kiểm tra
a) trạng thái kiểm soát của hệ thống đo trong thực nghiệm hiệu chuẩn.
b) giả định về tính tuyến tính, và
c) độ biến động của các phép đo là hàm của giá trị chấp nhận của RM.
5.4.2. Ước lượng hàm hiệu chuẩn tuyến tính với giả định độ lệch chuẩn dư không đổi.
5.4.3. Vẽ đồ thị hàm hiệu chuẩn và các số dư. Đồ thị số dư và một chỉ số quan trọng về sự lệch khỏi giả định về tính tuyến tính hay giả định độ lệch chuẩn dư không đổi. Nếu giả định về độ lệch chuẩn dư không đổi là đúng thì bỏ qua bước 5.4.4 và tiếp tục với bước 5.4.5. Nếu không thì thực hiện bước 5.4.4.
5.4.4. Ước lượng hàm hiệu chuẩn tuyến tính với giả định độ lệch chuẩn dư tỷ lệ thuận, vẽ đồ thị hàm hiệu chuẩn và các số dư.
5.4.5. Đánh giá sự không khớp của hàm hiệu chuẩn. Nếu độ biến động do không khớp tương đối lớn so với độ biến động do việc lặp lại các phép đo thì kiểm tra các quy trình tiếp theo trong quá trình thực nghiệm hiệu chuẩn và kiểm tra lại giả định về tính tuyến tính của hàm hiệu chuẩn. Nếu giả định về tính tuyến tính không đúng thì có thể sử dụng kỹ thuật đóng khung mô tả ở 8.3.
CHÚ THÍCH 2: Còn có các kỹ thuật khác, không thuộc phạm vi của tiêu chuẩn này, cho phép khớp dữ liệu theo đường cong bậc hai hay đa thức (xem tài liệu tham khảo [2] và [3]).
5.4.6. Chuyển đổi giá trị đo được sau này bằng hàm hiệu chuẩn
Điều tiếp theo mô tả sáu bước của chiến lược này. Điều 9 minh họa phương pháp cơ bản bằng ví dụ.
6. Các bước của phương pháp cơ bản
6.1. Vẽ đồ thị dữ liệu thu thập được trong quá trình thực nghiệm hiệu chuẩn
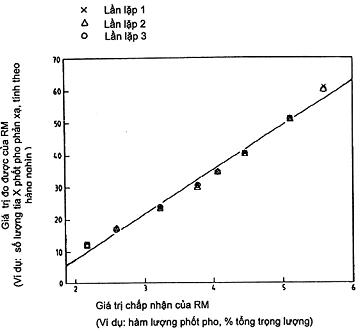
Hình 1 thể hiện đồ thị các giá trị đo được so với các giá trị chấp nhận tương ứng của RM. Hình 1 cũng như các hình từ 2 đến 5 thu được từ dữ liệu mô phỏng. Mục đích của năm đồ thị này là để minh họa loại thông tin có thể rút ra từ đồ thị. Một ví dụ hoàn chỉnh được diễn giải trong điều 8 với dữ liệu, đồ thị và phân tích.
Mục đích chính của đồ thị như cho trên Hình 1 là phát hiện bằng mắt mọi bất thường của hệ thống đo trong quá trình thực nghiệm hiệu chuẩn và để nhận biết các giá trị bất thường có thể có. Nếu có thể, ghi thứ tự cho các điểm dữ liệu và tìm hiểu xu hướng thời gian rõ ràng. Nếu một số dữ liệu được coi là đáng ngờ hoặc nếu xu hướng thời gian rõ ràng thì phải tiến hành kiểm tra để phát hiện nguyên nhân của các bất thường. Ngay khi nguyên nhân của các bất thường được loại trừ, cần lặp lại thực nghiệm hiệu chuẩn và thu thập dữ liệu mới để có thể thiết lập hàm hiệu chuẩn.
Nếu nguyên nhân đối với một hoặc rất ít giá trị bất thường được tìm thấy và nếu nguyên nhân này không ảnh hưởng đến các phép đo còn lại thì có thể loại bỏ các giá trị bất thường đó. Khi đó, thực nghiệm hiệu chuẩn trở nên không cân bằng, nghĩa là có số phép đo không bằng nhau Kn thay vì K cho mỗi RM. Việc ước lượng hàm hiệu chuẩn vẫn có thể tiến hành với công thức cho trong 6.2, 6.4 và 6.5 được thay bằng công thức trong Phụ lục B.
Hình 1 cũng cho phép chẩn đoán sớm giả định về tính tuyến tính của hàm hiệu chuẩn cũng như xem xét ban đầu về giả định độ lệch chuẩn dư không đổi. Có thể kiểm tra bằng mắt tính tuyến tính của hàm hiệu chuẩn bằng cách hình dung một đường thẳng thông qua dữ liệu được vẽ trên Hình 1 (có vẻ như có đoạn cong nhất định trong dữ liệu của Hình 1). Có thể kiểm tra giả định về độ lệch chuẩn dư không có đoạn cong nhất định trong dữ liệu của Hình 1). Có thể kiểm tra giả định về độ lệch chuẩn dư không đổi bằng cách nhìn vào phân bố các điểm trên Hình 1 đối với RM đã cho. Nếu có vẻ như sự phân bố này tăng lên với các giá trị chấp nhận của RM thì giả định về độ lệch chuẩn dư không đổi có thể là không đúng (đây không phải là trường hợp ở Hình 1). Một đồ thị phức tạp hơn để kiểm tra giả định về tính tuyến tính và độ lệch chuẩn dư không đổi được trình bày ở 6.3
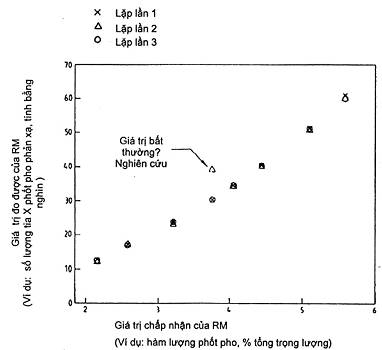
Hình 1 – Giản đồ dữ liệu thu thập trong quá trình thực nghiệm hiệu chuẩn
6.2. Ước lượng hàm hiệu chuẩn tuyến tính với giả định độ lệch chuẩn dư không đổi
6.2.1. Mô hình
Giả định về tính tuyến tính và độ lệch chuẩn dư không đổi có được nhờ mô hình
![]()
Trong đó
![]() là giá trị chấp nhận của RM thứ n (n = 1, …, N);
là giá trị chấp nhận của RM thứ n (n = 1, …, N);
![]() là phép đo thứ k của RM thứ n (k = 1, …, K);
là phép đo thứ k của RM thứ n (k = 1, …, K);
![]() đại diện giá trị mong đợi của phép đo RM thứ n;
đại diện giá trị mong đợi của phép đo RM thứ n;
![]() là độ lệch giữa ynk và giá trị mong đợi của phép đo RM thứ n (các độ lệch này được giả định là độc lập và có phân bố chuẩn với trung bình 0 và phương sai σ2)
là độ lệch giữa ynk và giá trị mong đợi của phép đo RM thứ n (các độ lệch này được giả định là độc lập và có phân bố chuẩn với trung bình 0 và phương sai σ2)
![]() là ba tham số cần ước lượng từ dữ liệu thu thập trong quá trình hiệu chuẩn;
là ba tham số cần ước lượng từ dữ liệu thu thập trong quá trình hiệu chuẩn;
![]() là giá trị chặn của hàm hiệu chuẩn,
là giá trị chặn của hàm hiệu chuẩn,
![]() là độ dốc của hàm hiệu chuẩn,
là độ dốc của hàm hiệu chuẩn,
![]() là thước đo độ chụm của hệ thống đo.
là thước đo độ chụm của hệ thống đo.
6.2.2. Ước lượng các tham số
Có thể có được ước lượng các tham số ![]() bằng cách sử dụng công thức dưới đây hoặc bằng cách chạy phần mềm hồi quy tuyến tính với hai cột có độ dài bằng nhau làm đầu vào, một cột y và một cột x.
bằng cách sử dụng công thức dưới đây hoặc bằng cách chạy phần mềm hồi quy tuyến tính với hai cột có độ dài bằng nhau làm đầu vào, một cột y và một cột x.
CHÚ THÍCH 3: Ước lượng tham số trong tiêu chuẩn này có ký hiệu ^ để phân biệt chúng với bản thân các tham số chưa biết.
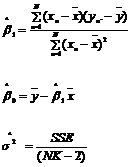
![]() Trong đó
Trong đó
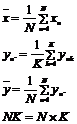
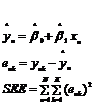
6.3. Đồ thị điểm hàm hiệu chuẩn và các số dư
Hình 2 và 3 được khuyến nghị để kiểm nghiệm sai lệch so với giả định nêu trong mô hình ở 6.2.
6.3.1. Đồ thị điểm hàm hiệu chuẩn
Trên Hình 2, hàm hiệu chuẩn ước lượng được thêm vào Hình 1.
Trước hết, đồ thị cho trên Hình 2 chủ yếu cho phép kiểm tra các tính toán nêu ở 6.2.2. Nó cũng giúp đưa ra kiểm tra bằng mắt giả định về tính tuyến tính của hàm hiệu chuẩn.
Hình 2 – Giản đồ đường cong hiệu chuẩn
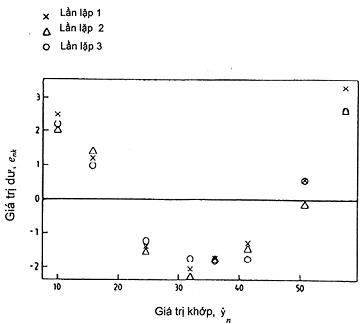
Hình 3 – Giản đồ đồ thị số dư với giá trị khớp
6.3.2. Đồ thị số dư so với giá trị khớp
Đồ thị số dư enk với giá trị ![]() khớp (Hình 3) là một công cụ hữu ích để phát hiện sai lệch so với hai giả định về tính tuyến tính và độ lệch chuẩn dư không đổi. Nếu hai giả định này đúng thì trên Hình 3 cần thể hiện một đồ thị các điểm phân bố ngẫu nhiên quanh điểm không. Sai lệch so với giả định về tính tuyến tính được chỉ ra qua dạng sắp xếp giữa số dư và các giá trị khớp (như trong trường hợp Hình 3). Sai lệch so với giả định về độ lệch chuẩn dư không đổi được chỉ ra qua sự phân tán dữ liệu tăng lên hay giảm đi theo giá trị khớp. Trên Hình 3, sự phân tán số dư đối với giá trị khớp bất kỳ gần như hoàn toàn không đổi. Vì vậy, giả định về độ lệch chuẩn dư không đổi là hợp lý trong tình huống này.
khớp (Hình 3) là một công cụ hữu ích để phát hiện sai lệch so với hai giả định về tính tuyến tính và độ lệch chuẩn dư không đổi. Nếu hai giả định này đúng thì trên Hình 3 cần thể hiện một đồ thị các điểm phân bố ngẫu nhiên quanh điểm không. Sai lệch so với giả định về tính tuyến tính được chỉ ra qua dạng sắp xếp giữa số dư và các giá trị khớp (như trong trường hợp Hình 3). Sai lệch so với giả định về độ lệch chuẩn dư không đổi được chỉ ra qua sự phân tán dữ liệu tăng lên hay giảm đi theo giá trị khớp. Trên Hình 3, sự phân tán số dư đối với giá trị khớp bất kỳ gần như hoàn toàn không đổi. Vì vậy, giả định về độ lệch chuẩn dư không đổi là hợp lý trong tình huống này.
CHÚ THÍCH 4: Hình 8 minh họa tình huống trong đó giả định về độ lệch chuẩn dư không đổi là không logic.
Nếu giả định về độ lệch chuẩn dư không đổi không đúng thì dữ liệu thu thập trong quá trình thực nghiệm hiệu chuẩn phải được phân tích lại. Đồ thị điểm về độ lệch chuẩn của các phép đo lặp của RM theo giá trị chấp nhận của chính RM đó sẽ chỉ ra giả định về độ lệch chuẩn dư tỷ lệ có hợp lý hay không. Xem Hình 9 về đồ thị này.
a) Nếu giả định về độ lệch chuẩn dư tỷ lệ có vẻ đúng thì có thể phân tích lại dữ liệu theo bước 6.4.
b) Nếu giả định về độ lệch chuẩn dư tỷ lệ không đúng nhưng có mô hình biểu thị quan hệ giữa độ lệch chuẩn dư và giá trị chấp nhận của RM (ví dụ tỷ lệ nghịch) thì có thể sử dụng cách tiếp cận tương tự như trình bày ở bước 6.4.
Nếu giả định về tính tuyến tính không đúng thì có thể sử dụng kỹ thuật đóng khung mô tả ở 8.3.
CHÚ THÍCH 5: Còn có các kỹ thuật khác, không thuộc phạm vi của tiêu chuẩn này, cho phép tìm dữ liệu qua đường cong bậc hai hay dạng hàm đa thức (xem tài liệu tham khảo [2] và [3]).
Cuối cùng, kiểm nghiệm giả định về tính độc lập và tính chuẩn các giá trị enk nằm ngoài phạm vi của tiêu chuẩn này. Hai giả định này rất cần thiết để xác định hiệu lực của bước 6.5 và cũng có thể kiểm tra bằng cách nghiên cứu các số dư. Ví dụ, đồ thị xác suất chuẩn của số dư cho phép kiểm tra giả định phân bố chuẩn và đồ thị số dư theo thời gian cho phép kiểm tra giả định về tính độc lập của các phép đo. Thông tin có thể thấy trong tài liệu tham khảo [3].
6.4. Ước lượng hàm hiệu chuẩn với giả định độ lệch chuẩn dư tỷ lệ và đồ thị điểm hàm hiệu chuẩn và số dư
6.4.1. Mô hình
Một mô hình khác ngoài mô hình nêu ở bước 6.2.1 là mô hình trong đó hàm hiệu chuẩn là tuyến tính nhưng độ lệch chuẩn dư tăng theo giá trị chấp nhận của RM. Điều này thu được trong mô hình.
![]()
Trong đó
xn là giá trị chấp nhận của RM thứ n ( n = 1, …, N);
ynk là phép đo thứ k của RM thứ n ( k = 1, …, K)
![]() đại diện giá trị mong đợi của phép đo RM thứ n;
đại diện giá trị mong đợi của phép đo RM thứ n;
hnk là độ lệch giữa ynk và giá trị mong đợi của phép đo RM thứ n (các độ lệch này được giả định là độc lập và có phân bố chuẩn với trung bình 0 và phương sai tỷ lệ với ![]() ); nghĩa là:
); nghĩa là:
![]()
![]() là ba tham số cần ước lượng từ dữ liệu thu thập trong quá trình hiệu chuẩn:
là ba tham số cần ước lượng từ dữ liệu thu thập trong quá trình hiệu chuẩn:
g0 và g1 tương ứng là giá trị chặn và độ dốc của hàm hiệu chuẩn,
![]() là thước đo độ chụm tương đối của hệ thống đo.
là thước đo độ chụm tương đối của hệ thống đo.
Mô hình này có thể chuyển thành mô hình tương đương với mô hình nêu trong 6.2.1; nghĩa là với sai số có phương sai không đổi. Việc chuyển đổi bao gồm chia cả hai vế của phương trình cho xn
![]()
Ta được
![]()
Hoặc, tương đương
![]()
Trong đó
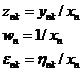
Mô hình mới này có thể được phân tích như trong 6.2 sau khi thực hiện việc thay thế đúng các số hạng.
6.4.2. Ước lượng các tham số
Có thể có được ước lượng các tham số ![]() bằng cách sử dụng công thức dưới đây hoặc bằng cách chạy phần mềm hồi quy tuyến tính có trọng số với ba cột có độ dài bằng nhau làm đầu vào, một cột y, một cột x và một cột cho các trọng số ( = 1/x2). Các đầu ra tương tự cũng có thể có được bằng cách sử dụng gói phần mềm hồi quy truyến tính không có trọng số nhưng với hai cột đầu vào là z và w.
bằng cách sử dụng công thức dưới đây hoặc bằng cách chạy phần mềm hồi quy tuyến tính có trọng số với ba cột có độ dài bằng nhau làm đầu vào, một cột y, một cột x và một cột cho các trọng số ( = 1/x2). Các đầu ra tương tự cũng có thể có được bằng cách sử dụng gói phần mềm hồi quy truyến tính không có trọng số nhưng với hai cột đầu vào là z và w.
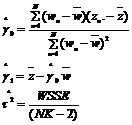
Trong đó
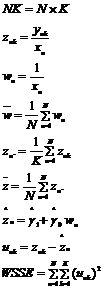
6.4.3. Đồ thị hàm hiệu chuẩn và các số dư
Như trong 6.3, hai đồ thị được khuyến nghị:
a) đồ thị hàm hiệu chuẩn ước lượng ![]() với dữ liệu của Hình 1;
với dữ liệu của Hình 1;
b) đồ thị số dư có trọng số unk theo giá trị khớp có trọng số ![]()
Giải thích các đồ thị này tương tự như của Hình 2 và 3.
6.5. Đánh giá sự không khớp của hàm hiệu chuẩn
6.5.1. Khái quát
Sau khi lập bảng ANOVA, tiến hành so sánh giữa
– độ biến độ do không khớp của mô hình được chọn ở 6.2 hoặc 6.4 và
– độ biến động của sai số thuần túy thể hiện hệ thống không có khả năng lặp lại các phép đo một cách chính xác.
So sánh như vậy có thể thực hiện được vì các phép đo đối với mỗi RM được tiến hành lặp lại.
Việc lựa chọn mức ý nghĩa a phụ thuộc vào ứng dụng cụ thể và tùy thuộc vào người sử dụng tiêu chuẩn này.
6.5.2. Mô hình có độ lệch chuẩn dư không đổi (xác định ở 6.2)
6.5.2.1. Bảng ANOVA cho trong Bảng 1 có thể thu được bằng cách sử dụng công thức dưới đây hoặc như đầu ra của hầu hết các phần mềm hồi quy tuyến tính.
Bảng 1 – Bảng ANOVA để so sánh sự không khớp và sai số thuần túy với giả định là độ lệch chuẩn dư không đổi
|
Nguồn |
Bậc tự do, DF |
Tổng bình phương, SS |
SS/DF |
Tỷ số F |
|
Hàm hiệu chuẩn Số dư
Không khớp
Sai số thuần túy
|
1 NK – 2
N – 2
NK – N |
SSR = SST – SSE SSE
SSE – SSP
SSP |
|
|
|
Tổng |
NK – 1 |
SST |
|
|
|
SSE được xác định ở 6.2.2 |
||||
6.5.2.2. Độ biến động do sai số thuần túy được ước lượng bằng ![]() . Độ biến động này độc lập với mô hình (
. Độ biến động này độc lập với mô hình (![]() ) khớp với dữ liệu. Độ biến động do không khớp được ước lượng bằng
) khớp với dữ liệu. Độ biến động do không khớp được ước lượng bằng ![]() . Phép thử xác nhận hiệu lực của mô hình nêu ở 6.2.1 được tiến hành bằng cách so sánh tỷ số
. Phép thử xác nhận hiệu lực của mô hình nêu ở 6.2.1 được tiến hành bằng cách so sánh tỷ số ![]() /
/![]() với F(1-a)(N – 2);NK – N), trong đó F(1-a)(N – 2);NK – N) là phân vị (1 – a) của phân bố F với N – 2 và NK – N bậc tự do.
với F(1-a)(N – 2);NK – N), trong đó F(1-a)(N – 2);NK – N) là phân vị (1 – a) của phân bố F với N – 2 và NK – N bậc tự do.
a) Nếu ![]() /
/![]() không lớn hơn F(1-a)(N – 2);NK – N) thì không có bằng chứng để loại bỏ mô hình tuyến tính.
không lớn hơn F(1-a)(N – 2);NK – N) thì không có bằng chứng để loại bỏ mô hình tuyến tính.
b) Nếu ![]() /
/![]() lớn hơn F(1-a)(N – 2);NK – N) thì các nguyên nhân tiềm ẩn gây ra độ biến động lớn do không khớp so với biến thiên sai số thuần túy cần được nghiên cứu. Một nguyên nhân phổ biến là giả định hàm hiệu chuẩn tuyến tính không thỏa đáng (xem Hình 2 và 3). Một nguyên nhân khác có thể là điều kiện thực hiện thực nghiệm hiệu chuẩn (ví dụ các phép lặp có thể không được lặp thực sự mà chỉ là lặp lại cùng một số đọc).
lớn hơn F(1-a)(N – 2);NK – N) thì các nguyên nhân tiềm ẩn gây ra độ biến động lớn do không khớp so với biến thiên sai số thuần túy cần được nghiên cứu. Một nguyên nhân phổ biến là giả định hàm hiệu chuẩn tuyến tính không thỏa đáng (xem Hình 2 và 3). Một nguyên nhân khác có thể là điều kiện thực hiện thực nghiệm hiệu chuẩn (ví dụ các phép lặp có thể không được lặp thực sự mà chỉ là lặp lại cùng một số đọc).
6.5.3. Mô hình có độ lệch chuẩn dư tỷ lệ (xác định ở 6.4)
Nếu mô hình có độ lệch chuẩn dư tỷ lệ được sử dụng thì bảng ANOVA được hình thành như cho trên Bảng 2.
Phép thử, giải thích, kết luận và chú ý áp dụng cho ![]() /
/![]() như cho
như cho ![]() /
/![]() tương tự mô tả trong 6.5.2.2.
tương tự mô tả trong 6.5.2.2.
Bảng 2 – Bảng ANOVA để so sánh sự không khớp và sai số thuần túy với giả định là độ lệch chuẩn dư tỷ lệ
|
Nguồn |
Bậc tự do, DF |
Tổng bình phương, SS |
SS/DF |
Tỷ số F |
|
Hàm hiệu chuẩn Số dư
Không khớp
Sai số thuần túy
|
1
NK – 2
N – 2
NK – N |
WSSR = WSST – WSSE
WSSE
WSSE – WSSP
WSSP |
|
|
|
Tổng |
NK – 1 |
WSST |
|
|
|
WSSE được xác định ở 6.4.2 |
||||
6.6. Chuyển đổi các giá trị đo sau này bằng hàm hiệu chuẩn
Khi thực hiện hiệu chuẩn đã thực hiện, các giá trị đo được của các đại lượng mới chưa biết (phân biệt với các hiệu chuẩn đã biết giá trị thực hoặc giá trị chấp nhận) sẽ được chuyển đổi bằng hàm hiệu chuẩn. Việc chuyển đổi các giá trị đo này sẽ dẫn đến một giá trị đơn ![]() ước lượng cho giá trị thực của đại lượng chưa biết. Việc chuyển đổi phụ thuộc vào giả định đưa ra liên quan đến phương sai dư và được thực hiện như dưới đây.
ước lượng cho giá trị thực của đại lượng chưa biết. Việc chuyển đổi phụ thuộc vào giả định đưa ra liên quan đến phương sai dư và được thực hiện như dưới đây.
Một đại lượng mới chưa biết được đo p lần, dẫn đến p phép đo ![]() . Trung bình
. Trung bình ![]() của p phép đo này thu được là
của p phép đo này thu được là
![]()
Nếu p = 1 thì ![]() =
= ![]() .
.
a) Nếu mô hình với độ lệch chuẩn dư không đổi được chọn thì
![]()
b) Nếu mô hình với độ lệch chuẩn dư tỷ lệ được chọn thì
![]()
Tiêu chuẩn này không đưa ra khoảng tin cậy, từng khoảng riêng lẻ (xem tài liệu tham khảo [2] hay đồng thời (xem tài liệu tham khảo [4] và [5]), cho ước lượng của các đại lượng mới chưa biết dựa trên bản thân thực nghiệm hiệu chuẩn. Thay vào đó, tiêu chuẩn này đưa ra phương pháp kiểm soát, trong số các công dụng khác, phương pháp này cho phép suy ra khoảng tin cậy dựa trên độ biến động quan sát được khi theo dõi một số ít RM trong khoảng thời gian.
7. Phương pháp kiểm soát
7.1. Khái quát
Khi hàm hiệu chuẩn được sử dụng trong một khoảng thời gian kéo dài thì nên thực hiện phương pháp kiểm soát để kiểm tra hiệu lực của đường cong hiệu chuẩn cũng như để nhận biết và từ đó loại trừ các nguồn biến động không mong muốn. Phương pháp kiểm soát này theo dõi hệ thống đo trên cơ sở thường xuyên để phát hiện nhanh khi hệ thống thể hiện bất thường hoặc thay đổi, từ đó làm cho hàm hiệu chuẩn trở nên vô ích, nếu không nói là có hại.
Việc phát hiện đạt được bằng cách theo dõi các giá trị đo được (sau đó chuyển đổi bằng hàm hiệu chuẩn) của tập m RM bằng kỹ thuật đồ kiểm soát.
CHÚ THÍCH 6: Phương pháp tiếp cận này mở rộng biểu đồ kiểm soát truyền thống mô tả trong ISO 7870 [6] và ISO 8258 [7].
Biểu đồ kiểm soát trước tiên được thiết lập từ giá trị thu được trong quá trình thực hiện hiệu chuẩn. Sau đó, biểu đồ kiểm soát được sử dụng để quyết định việc hàm hiệu chuẩn có cần được ước lượng lại hay không. Biểu đồ kiểm soát tương tự cũng được dùng để ước lượng độ không đảm bảo của phép đo sau khi chúng đã được chuyển đổi bằng hàm hiệu chuẩn.
7.2. Tính giới hạn kiểm soát trên và dưới
7.2.1. Mô hình với độ lệch chuẩn dư không đổi
a) Tính giới hạn kiểm soát trên Ud và giới hạn kiểm soát dưới Ld
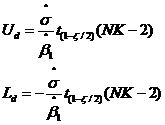
Trong đó
![]() là căn bậc hai của ước lượng
là căn bậc hai của ước lượng ![]() thu được từ thực nghiệm hiệu chuẩn (xem 6.2.2)
thu được từ thực nghiệm hiệu chuẩn (xem 6.2.2)
(NK – 2) là số bậc tự do đi kèm với ước lượng của s2 (xem 6.5);
![]() là ước lượng của β1 thu được từ thực nghiệm hiệu chuẩn (xem 6.2.2);
là ước lượng của β1 thu được từ thực nghiệm hiệu chuẩn (xem 6.2.2);
![]() là mức có ý nghĩa được chọn cho biểu đồ kiểm soát;
là mức có ý nghĩa được chọn cho biểu đồ kiểm soát;
![]() là phân vị (
là phân vị (![]() ) của phân bố t với NK – 2 bậc tự do; nghĩa là
) của phân bố t với NK – 2 bậc tự do; nghĩa là
![]()
![]() là mức ý nghĩa đi kèm với mỗi RM đơn lẻ với giới hạn Ud và Ld sao cho mức ý nghĩa tổng thể a thu được đồng thời cho tất cả m RM;
là mức ý nghĩa đi kèm với mỗi RM đơn lẻ với giới hạn Ud và Ld sao cho mức ý nghĩa tổng thể a thu được đồng thời cho tất cả m RM; ![]() thu được (đối với các giá trị α nhỏ) là
thu được (đối với các giá trị α nhỏ) là
![]() =
= ![]()
b) Vẽ các giới hạn Ud và Ld trên biểu đồ kiểm soát.
7.2.2. Mô hình với độ lệch chuẩn dư tỷ lệ
a) Tính giới hạn kiểm soát trên Uc và giới hạn kiểm soát dưới Lc
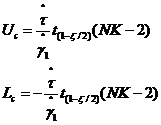
Trong đó
![]() là căn bậc hai của ước lượng
là căn bậc hai của ước lượng ![]() thu được từ thực nghiệm hiệu chuẩn (xem 6.4.2)
thu được từ thực nghiệm hiệu chuẩn (xem 6.4.2)
(NK – 2) là số bậc tự do đi kèm với ước lượng của ![]() (xem 6.5);
(xem 6.5);
![]() là ước lượng của
là ước lượng của ![]() thu được từ thực nghiệm hiệu chuẩn (xem 6.4.2);
thu được từ thực nghiệm hiệu chuẩn (xem 6.4.2);
CHÚ THÍCH 7: ![]() và
và ![]() như được xác định trong 7.2.1 a).
như được xác định trong 7.2.1 a).
b) Vẽ các giới hạn Uc và Lc trên biểu đồ kiểm soát.
7.3. Tập hợp và vẽ đồ thị dữ liệu
7.3.1. Chọn m RM sao cho giá trị chấp nhận của chúng bao trùm dãy giá trị gặp phải trong điều kiện hoạt động bình thường của hệ thống đo. Cần ít nhất là hai RM. Khuyến cáo sử dụng ba RM. Nên ưu tiên nhưng không bắt buộc sử dụng các RM khác so với loại đã sử dụng trong quá trình thực nghiệm hiệu chuẩn.
7.3.2. Trên cơ sở thường xuyên (ví dụ một lần một ngày hoặc một lần mỗi ca), thực hiện một phép đo trên mỗi trong số m RM này.
7.3.3. Thu được các giá trị chuyển đổi của mỗi trong số m RM (xem 6.6). Các giá trị chuyển đổi này được gọi là ![]() với i = 1, … , m.
với i = 1, … , m.
7.3.4. Tính các hiệu di giữa các giá trị chuyển đổi ![]() và giá trị chấp nhận của các RM này, xi là
và giá trị chấp nhận của các RM này, xi là ![]()
7.3.5. Nếu mô hình chuẩn giả định độ lệch chuẩn dư không đổi, xem các hiệu di như là giá trị cần kiểm soát.
Nếu mô hình hiệu chuẩn giả định độ lệch chuẩn dư tỷ lệ, chuẩn hóa các hiệu di bằng cách chia chúng cho xi. Xem các giá trị ci thu được như là giá trị cần kiểm soát, trong đó
![]()
7.3.6. Vẽ đồ thị các giá trị kiểm soát thích hợp (di hoặc ci) theo thời gian tại đó m RM được đo trên biểu đồ kiểm soát. Hình 4 minh họa biểu đồ kiểm soát đối với mô hình độ lệch chuẩn dư không đổi. Biểu đồ kiểm soát tương tự có thể được vẽ cho mô hình độ lệch chuẩn dư tỷ lệ (xem Hình 12).
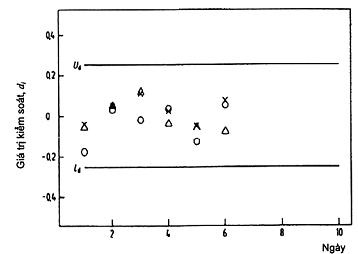
CHÚ DẪN: x = RM với giá trị dưới, Δ = RM với giá trị ở giữa, o = RM với giá trị trên
Hình 4 – Giản đồ biểu đồ kiểm soát để xác nhận hiệu lực của đường cong hiệu chuẩn với giả định độ lệch chuẩn dư không đổi
7.4. Quyết định về tình trạng của hệ thống
Nếu một hoặc nhiều giá trị di nằm ngoài giới hạn kiểm soát Ud và Ld đối với mô hình độ lệch chuẩn dư không đổi, thì hệ thống được công bố là nằm ngoài tầm kiểm soát tại thời điểm đó. Tập m RM cần được đo lại. Nếu ít nhất một trong số các phép đo mớ từ m RM vẫn nằm ngoài giới hạn thì phải thực hiện nghiên cứu tại điểm đó để xác định nguyên nhân của vấn đề. Tùy theo tính chất của vấn đề, hàm hiệu chuẩn có thể cần được ước lượng lại từ một thực nghiệm hiệu chuẩn mới.
Các kết luận tương tự cũng có được đối với mô hình có độ lệch chuẩn dư tỷ lệ bằng cách so sánh các giá trị ci với các giới hạn Uc và Lc.
7.5. Ước lượng độ không đảm bảo của giá trị chuyển đổi
7.5.1. Ước lượng trong quá trình xác nhận hiệu lực của hàm hiệu chuẩn đã cho
Đối với hàm hiệu chuẩn chịu phương pháp kiểm soát, độ không đảm bảo của giá trị chuyển đổi được tính gần đúng bằng phương sai chung của giá trị kiểm soát từ hai RM (trong số m RM được chọn cho phương pháp kiểm soát): RM có giá trị nhỏ nhất và lớn nhất. Điều này được giải thích bằng thực tế là các giá trị chuyển đổi ở cuối dãy giá trị gặp phải trong quá trình thực nghiệm hiệu chuẩn thường có phương sai lớn hơn so với các giá trị ở giữa của dãy đó. Vì vậy, khoảng tin cậy của giá trị chuyển đổi rút ra từ khoảng biến thiên của hai RM cực trị là gần đúng đối với các giá trị ở cuối dãy của ứng dụng và duy trì không đổi đối với các giá trị ở giữa dãy.
Để tính khoảng tin cậy này, thực hiện quy trình nêu trong 7.5.1.1 cho mô tả thích hợp (độ lệch chuẩn dư không đổi hoặc tỷ lệ).
7.5.1.1. Mô hình với độ lệch chuẩn dư không đổi
Lấy ![]() và
và ![]() làm giá trị kiểm soát của RM nhỏ nhất và lớn nhất, trong đó j đại diện cho lần tại đó các phép đo được thực hiện. Sau đó, qua khoảng J lần khi hệ thống đo nằm trong tình trạng kiểm soát thống kê, độ lệch chuẩn của giá chuyển đổi được tính gần đúng bằng
làm giá trị kiểm soát của RM nhỏ nhất và lớn nhất, trong đó j đại diện cho lần tại đó các phép đo được thực hiện. Sau đó, qua khoảng J lần khi hệ thống đo nằm trong tình trạng kiểm soát thống kê, độ lệch chuẩn của giá chuyển đổi được tính gần đúng bằng
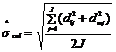
Với 2J bậc tự do.
Khoảng tin cậy gần đúng đối với giá trị thực chưa biết của đại lượng ước lượng bởi giá trị chuyển đổi ![]() (rút ra từ p phép đo thực hiện trong một khoảng thời gian ngắn) với mức tin cậy (1 – α) thu được là
(rút ra từ p phép đo thực hiện trong một khoảng thời gian ngắn) với mức tin cậy (1 – α) thu được là ![]()
Trong đó ![]() là phân vị (1 – α/2) của phân bố t với 2J bậc tự do.
là phân vị (1 – α/2) của phân bố t với 2J bậc tự do.
7.5.1.2. Mô hình với độ lệch chuẩn dư tỷ lệ
Lấy ![]() và
và ![]() là giá trị kiểm soát của RM nhỏ nhất và lớn nhất, trong đó j đại diện cho lần tại đó các phép đo được thực hiện. Sau đó, qua khoảng J lần khi hệ thống đo nằm trong tình trạng kiểm soát thống kê, hệ số biến động của giá trị chuyển đổi được tính gần đúng bằng
là giá trị kiểm soát của RM nhỏ nhất và lớn nhất, trong đó j đại diện cho lần tại đó các phép đo được thực hiện. Sau đó, qua khoảng J lần khi hệ thống đo nằm trong tình trạng kiểm soát thống kê, hệ số biến động của giá trị chuyển đổi được tính gần đúng bằng
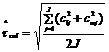
Với 2J bậc tự do.
Khoảng tin cậy gần đúng đối với giá trị thực chưa biết của đại lượng ước lượng bởi giá trị chuyển đổi ![]() (rút ra từ p phép đo thực hiện trong một khoảng thời gian ngắn) với mức tin cậy (1 – α) thu được là
(rút ra từ p phép đo thực hiện trong một khoảng thời gian ngắn) với mức tin cậy (1 – α) thu được là ![]()
Trong đó ![]() là phân vị (1 – α/2) của phân bố t với 2J bậc tự do.
là phân vị (1 – α/2) của phân bố t với 2J bậc tự do.
7.5.2. Ước lượng trong khoảng thời gian bao gồm việc hiệu chuẩn lại
Để đảm bảo rằng độ biến động do quy trình hiệu chuẩn gây ra được bao gồm trong tuyên bố về độ không đảm bảo, lấy một tập của các giá trị kiểm soát (![]() và
và ![]() ) hoặc (
) hoặc (![]() và
và ![]() ) từ mỗi khoảng hiệu chuẩn và sử dụng công thức tương tự cho
) từ mỗi khoảng hiệu chuẩn và sử dụng công thức tương tự cho ![]() hoặc
hoặc ![]() , trong đó j bây giờ là số lần hiệu chuẩn lại.
, trong đó j bây giờ là số lần hiệu chuẩn lại.
8. Hai lựa chọn phương pháp cơ bản
8.1. Khái quát
Trong điều kiện đặc biệt, hai phương pháp thay thế nhau có thể sử dụng để hiệu chuẩn quá trình đo. Hai phương pháp này là trường hợp đặc biệt thực sự của phương pháp cơ bản, trong đó chỉ một hoặc hai RM được sử dụng. Phương pháp hiệu chuẩn một điểm là kỹ thuật nhanh cho phép “hiệu chuẩn lại” một hệ thống đo khi không có nghi ngờ về tính tuyến tính của hàm hiệu chuẩn. Phương pháp đóng khung là kỹ thuật tiêu tốn nhân lực cho phép xác định giá trị của đại lượng chưa biết với độ chụm cao và với một tập tối thiểu các giả định.
8.2. Phương pháp hiệu chuẩn một điểm
8.2.1. Khái quát
Phương pháp này hữu ích đối với việc hiệu chuẩn lại nhanh không có nghi ngờ về tính tuyến tính của hàm hiệu chuẩn trong toàn dãy [0, … , M]. “Điểm không” thu được bằng cách điều chỉnh một số mặt số để đảm bảo rằng đại lượng chưa biết có giá trị 0 thực sự được đo là bằng 0. Chỉ mẫu trắng (đại lượng có giá trị thực 0) và một RM được sử dụng trong phương pháp này.
Cần chú ý rằng, trước đây, phương pháp này được gọi là hiệu chuẩn một điểm nhưng trên thực tế đây là hiệu chuẩn hai điểm tiến hành với một mẫu trắng và một RM. “Hiệu chuẩn một điểm” này là một phương pháp yếu và bất định vì tính không chắc chắn của điểm không. Không nên khuyến nghị phương pháp này cho mục đích hiệu chuẩn mà chủ yếu để kiểm tra hàm hiệu chuẩn tuyến tính hiện có.
8.2.2. Giả định
Giả định rằng:
a) không có sai số trong giá trị chấp nhận riêng của RM và mẫu trắng sử dụng với phương pháp này (giả định không được kiểm chứng);
b) hàm hiệu chuẩn là tuyến tính trong toàn dãy [0, …, M] (giả định không được kiểm chứng);
c) độ lệch chuẩn dư là hằng số (giả định không được kiểm chứng).
8.2.3. Thực nghiệm hiệu chuẩn một điểm
a) Điều kiện thực nghiệm: điều kiện thực nghiệm cần tương tự như điều kiện hoạt động bình thường của hệ thống đo.
b) Chọn RM: trong thực nghiệm này chỉ sử dụng RM có giá trị chấp nhận lớn hơn (càng nhiều càng tốt) so với giá trị gặp phải trong điều kiện bình thường của hệ thống đo.
c) Số lần gặp: RM cần được đo ít nhất hai lần.
8.2.4. Ước lượng hàm hiệu chuẩn
8.2.4.1. Mô hình
Mô hình này tương tự với mô hình phương pháp cơ bản với phương sai dư không đổi ở 6.2.1 nhưng không có phần chặn. Mô hình này là
![]()
Trong đó
x là giá trị chấp nhận của RM duy nhất được sử dụng;
yk là phép đo thứ k của RM đó (k = 1, …., K);
εk là độ lệch giữa yk và giá trị mong muốn của phép đo RM (độ lệch này được giả định là độc lập và phân bố chuẩn với trung bình 0 và phương sai ![]() );
);
![]() là hai tham số cần ước lượng từ dữ liệu thu thập trong quá trình thực nghiệm.
là hai tham số cần ước lượng từ dữ liệu thu thập trong quá trình thực nghiệm.
8.2.4.2. Ước lượng b và s2
Ước lượng này thu được từ công thức sau:
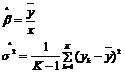
Trong đó
![]()
8.2.4.3. Vẽ đồ thị dữ liệu
Vẽ đồ thị dữ liệu thu thập được trong quá trình thực nghiệm, như cho trên Hình 5.
Đồ thị trên Hình 5 cho phép nhận biết bằng mắt các giá trị bất thường tiềm ẩn cho nghiên cứu. Đồ thị cũng thể hiện hàm hiệu chuẩn tuyến tính giới hạn đi qua gốc.
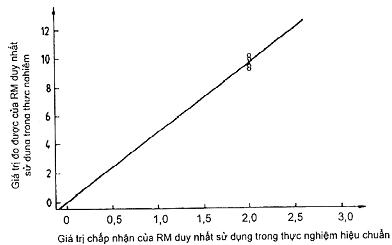
Hình 5 – Giản đồ dữ liệu trong thực nghiệm hiệu chuẩn một điểm
8.2.5. Chuyển đổi các phép đo sau này với hàm hiệu chuẩn
Đại lượng chưa biết được đo p lần, dẫn đến p phép đo y01, y02, …, yop. Trung bình ![]() của p phép đo này thu được là
của p phép đo này thu được là
![]()
Nếu p = 1 thì ![]() . Việc chuyển đổi các phép đo này sẽ dẫn đến một giá trị đơn được ghi lại là
. Việc chuyển đổi các phép đo này sẽ dẫn đến một giá trị đơn được ghi lại là ![]() .
.
CHÚ THÍCH 8: Về nguyên tắc, mẫu trắng không phải luôn có giá trị thực bằng 0 nhưng thay vào đó nó có giá trị chấp nhận là xb, có phép đo là yb. Nếu xb là không đáng kể thì có thể sử dụng phương pháp hiệu chuẩn một điểm nêu ở 8.2.3 với các sửa đổi dưới đây.
a) Đo mẫu trắng và điều chỉnh số của phương tiện đo về số đọc yb.
b) Đo RM duy nhất sử dụng, như trong trường hợp mẫu trắng với giá trị 0.
c) Mô hình trở thành
![]()
d) Ước lượng của β trở thành
![]()
e) Ước lượng của ![]() không đổi.
không đổi.
f) Ước lượng giá trị thực của đại lượng chưa biết đo p lần (y01, y02, … , y0p) là
![]()
8.3. Kỹ thuật đóng khung
8.3.1. Khái quát
Phương pháp này hữu ích khi có nghi ngờ về tuyến tính của hàm hiệu chuẩn trong toàn dãy giá trị gặp phải trong hoạt động bình thường của hệ thống đo. Phương pháp này cũng hữu ích khi có vấn đề nào đó về độ ổn định của quá trình đo. Nguyên tắc của phương pháp này bao gồm trong việc rút ngắn càng nhiều càng tốt khoảng ở đó tính tuyến tính của hàm hiệu chuẩn được giả định. Điều này dẫn đến bao quanh càng sát càng tốt (hay khung) giá trị của đại lượng chưa biết bằng hai giá trị của RM. Vì việc bao sát từng đại lượng chưa biết bằng hai RM và do khoảng thời gian ngắn cần thiết cho quy trình này (thời gian để đo đại lượng chưa biết và hai RM) nên kỹ thuật đóng khung thường cho độ chính xác cao hơn trong việc xác định giá trị chuyển đổi của đại lượng chưa biết.
Đại lượng chưa biết và hai RM được đo cùng nhau. Giá trị của đại lượng chưa biết được ước lượng trực tiếp, dựa trên nội suy tuyến tính giữa các giá trị của hai RM.
8.3.2. Giả định
Vì chỉ sử dụng hai RM nên kỹ thuật đóng khung không cho phép kiểm chứng bất kỳ giả định nào trong số các giả định sau:
a) không sai số trong giá trị chấp nhận của RM;
b) hàm hiệu chuẩn giữa hai RM là tuyến tính;
c) độ lệch chuẩn dư là hằng số.
8.3.3. Thực nghiệm đóng khung
a) Điều kiện thực nghiệm: điều kiện thực nghiệm cần sao cho độ biến động giữa các phép đo của cùng một RM càng nhỏ càng tốt.
b) Chọn RM: khoảng giá trị nằm giữa hai RM cần càng nhỏ càng tốt và phải chứa giá trị của đại lượng chưa biết cần đo.
c) Số lượng RM: hai RM được sử dụng cho mỗi đại lượng chưa biết.
d) Số lần lặp: Cả hai RM và đại lượng chưa biết cần được đo ít nhất hai lần.
8.3.4. Ước lượng đại lượng chưa biết
8.3.4.1. Mô hình
Mô hình này tương tự với mô hình phương pháp cơ bản với độ lệch chuẩn dư không đổi (xem 6.2), nghĩa là
![]()
Trong đó
i là chỉ số đề cập đến cả RM (i = 1, 2) cũng như đại lượng chưa biết ( i = 0);
x1 và x2 là giá trị chấp nhận của các RM;
x0 là giá trị thực của đại lượng chưa biết;
y1k, y2k và y0k là phép đo của hai RM và đại lượng chưa biết (k = 1, …, K);
![]() là độ lệch giữa yik và giá trị mong muốn của phép đo RM hoặc đại lượng chưa biết (tùy thuộc vào giá trị của i) (độ lệch này được giả định là phân bố chuẩn trung bình 0 và phương sai
là độ lệch giữa yik và giá trị mong muốn của phép đo RM hoặc đại lượng chưa biết (tùy thuộc vào giá trị của i) (độ lệch này được giả định là phân bố chuẩn trung bình 0 và phương sai ![]() );
);
![]() là bốn tham số cần ước lượng từ dữ liệu thu thập trong quá trình thực nghiệm khung ( không quan tâm đến
là bốn tham số cần ước lượng từ dữ liệu thu thập trong quá trình thực nghiệm khung ( không quan tâm đến ![]() trừ khi chúng tác động đến tham số x0).
trừ khi chúng tác động đến tham số x0).
8.3.4.2. Ước lượng x0 và phương sai dư ![]()
Các ước lượng này thu được từ công thức sau:
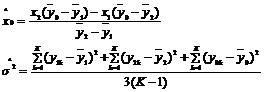
Trong đó
![]()
Khi i = 0, 1, 2
9. Ví dụ
9.1. Khái quát
Ví dụ này minh họa phương pháp cơ bản đối với việc ước lượng hàm hiệu chuẩn tuyến tính cho hệ thống đo và phương pháp kiểm soát dùng cho việc theo dõi hệ thống đo đó. Ví dụ được dựa trên tài liệu tham khảo [8].
9.2. Phương pháp cơ bản
9.2.1. Cơ sở và dữ liệu
Phép đo khoảng cách dòng trong mạng che quang mạch tích hợp trong dải từ 0,5 μm đến 12 μm có thể được thực hiện với hệ thống quang – ảnh (kính hiển vi quang lắp phụ kiện đo). Hệ thống này có thể được hiệu chuẩn bằng cách sử dụng mẫu chuẩn tiêu chuẩn SRM – 474 do Viện Chuẩn và Công Nghệ quốc gia (NIST) phát hành. SRM-474 có (trong số các nội dung khác) một hàng gồm mười khoảng cách bố trí ngẫu nhiên trong dải từ 0,5 μm đến 12 μm.
Ví dụ này mô tả thực nghiệm hiệu chuẩn thực hiện trên hệ thống quang-ảnh. Một khoảng trong số mười khoảng cách dòng của chuẩn đo được bốn lần. Những lần lặp này được thực hiện ở khoảng cách 2 tuần để đảm bảo sự độc lập giữa các phép đo. Dữ liệu trình bày trong Bảng 3 gồm bốn (K = 4) phép đo lặp trên mười (N = 10) khoảng cách dòng trong đó NIST cung cấp giá trị chấp nhận.
9.2.2. Đồ thị dữ liệu
Đồ thị dữ liệu thu thập trong quá trình thực nghiệm, như cho trên Hình 6, không nhận biết các giá trị bất thường rõ ràng hay biểu hiện bất thường của hệ thống trong quá trình thực nghiệm hiệu chuẩn. Đồ thị chứng minh giả định về tính tuyến tính của hàm hiệu chuẩn và đưa ra câu hỏi về giả định độ lệch chuẩn dư không đổi, vì sự phân bố của dữ liệu đối với giá trị NIST cho trước đó có chiều hướng tăng nhẹ với giá trị NIST đó.
Bảng 3 – Thực nghiệm hiệu chuẩn đối với khoảng cách dòng
Giá trị tính bằng micrômét
|
Giá trị NIST |
Giá trị đo được |
|||
|
xn |
Lần lặp 1 yn1 |
Lần lặp 2 yn2 |
Lần lặp 3 yn3 |
Lần lặp 4 yn4 |
|
6,19 9,17 1,99 7,77 4,00 10,77 4,78 2,99 6,98 9,98 |
6,31 9,27 2,21 8,00 4,27 10,93 4,95 3,24 7,14 10,23 |
6,27 9,21 2,19 7,81 4,15 10,73 4,87 3,17 7,07 10,02 |
6,31 9,34 2,22 7,95 4,15 10,92 5,00 3,21 7,18 10,07 |
6,28 9,23 2,20 7,84 4,15 10,89 5,00 3,21 7,20 10,17 |
X Lần lặp 1
O Lần lặp 2
Δ Lần lặp 3
* Lần lặp 4
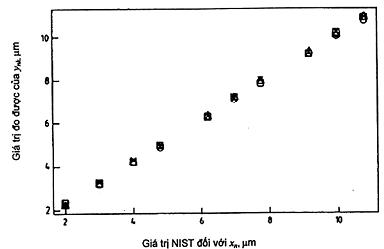
Hình 6 – Dữ liệu thu thập trong quá trình hiệu chuẩn thực nghiệm đối với khoảng cách dòng
9.2.3. Ước lượng hàm hiệu chuẩn tuyến tính với giả định độ lệch chuẩn dư không đổi
Công thức cho trong 6.2.2 dẫn đến:
a) N = 10, K = 4
b) ![]()
c) yi. như cho trong Bảng 4
d) ![]()
e) SSE = 0,1462
f) ![]()
g) ![]()
h) ![]()
Hàm hiệu chuẩn là
![]()
Giá trị khớp ![]() thu được bằng cách thay x trong công thức này bằng giá trị NIST xn liệt kê trong Bảng 3.
thu được bằng cách thay x trong công thức này bằng giá trị NIST xn liệt kê trong Bảng 3.
Các số dư thu được là
![]()
Các số dư này được liệt kê trong Bảng 5.
Bảng 4 – Giá trị của yi.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
yi. |
6,292 |
9,263 |
2,205 |
7,900 |
4,180 |
10,868 |
4,955 |
3,208 |
7,148 |
10,12 |
Bảng 5 – Hiệu chuẩn tuyến tính với giả định độ lệch chuẩn dư không đổi
Giá trị tính bằng micromét
|
Giá trị NIST xn |
Giá trị khớp
|
Giá trị dư |
|||
|
en1 |
en2 |
en3 |
en4 |
||
|
6,19 9,17 1,99 7,77 4,00 10,77 4,78 2,99 6,98 9,98 |
6,345 5 9,286 9 2,200 0 7,905 0 4,183 9 10,866 2 4,953 8 3,187 0 7,125 3 10,086 4 |
-0,035 5 -0,016 9 0,010 0 0,095 0 0,086 1 0,063 8 -0,003 8 0,053 0 0,014 7 0,143 6 |
-0,075 5 -0,076 9 -0,010 0 -0,095 0 -0,033 9 -0,136 2 -0,083 8 -0,017 0 -0,055 3 -0,066 4 |
-0,035 5 0,053 1 0,020 0 0,045 0 -0,033 9 0,053 8 0,046 2 0,023 0 0,054 7 -0,016 4 |
-0,065 5 -0,056 9 0,000 0 -0,065 0 -0,033 9 0,023 8 0,046 2 0,023 0 0,074 7 0,083 6 |
X Lần lặp 1
O Lần lặp 2
Δ Lần lặp 3
* Lần lặp 4
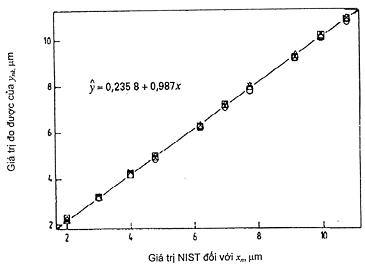
Hình 7 – Đường cong hiệu chuẩn cho khoảng cách dòng với giả định độ lệch chuẩn dư không đổi
9.2.4. Đồ thị hàm hiệu chuẩn và số dư
Đồ thị hàm hiệu chuẩn (Hình 7) xác nhận rằng hàm hiệu chuẩn tuyến tính có vẻ thích hợp.
Đồ thị số dư (Hình 8) cho thấy rằng lần lặp 2 có các giá trị dư thấp hơn phù hợp so với các lần lặp khác. Các giá trị dư thấp hơn này có thể truy về dữ liệu gốc ở Bảng 3 với giá trị của lần lặp 2 thấp hơn so với các lần lặp khác. Không có giải thích rõ ràng cho hiện tượng này và dữ liệu của lần lặp 2 được giữ làm đại diện cho biểu hiện của hệ thống đo trong điều kiện làm việc bình thường.
Một mô hình phức tạp hơn hai mô hình đề xuất tương ứng ở 6.2.1 và 6.4.1 có thể được sử dụng để phân tích dữ liệu này nhằm tính đến những khác biệt hệ thống giữa các lần lặp. Với mục đích đơn giản và minh họa cho phương pháp cơ bản và phương pháp kiểm soát, ảnh hưởng này sẽ được bỏ qua và chiến lược hiện tại cũng như mô hình đi kèm sẽ được tiếp tục.
Hình 8 cũng chỉ ra rằng giả định về độ lệch chuẩn dư không đổi có vẻ không đúng. Gợi ý này được khẳng định với Hình 9 cho thấy đồ thị độ lệch chuẩn của các phép đo lặp RM theo giá trị chấp nhận của RM đó.
X Lần lặp 1
O Lần lặp 2
Δ Lần lặp 3
* Lần lặp 4
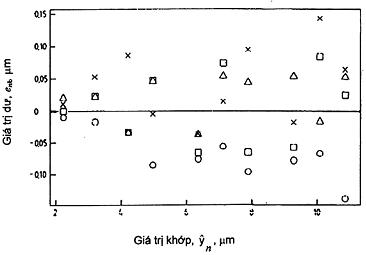
Hình 8 – Số dư theo giá trị khớp cho khoảng cách dòng với giả định độ lệch chuẩn dư không đổi
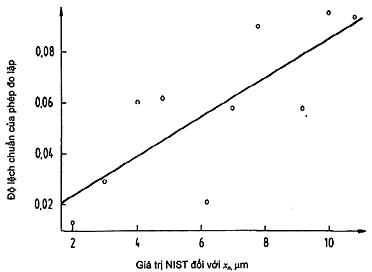
Hình 9 – Độ lệch chuẩn như phép đo lặp cho khoảng cách dòng theo giá trị NIST
9.2.5. Ước lượng hàm hiệu chuẩn với giả định độ lệch chuẩn dư tỷ lệ
Ước lượng hàm hiệu chuẩn với giả định độ lệch chuẩn dư tỷ lệ và đồ thị hàm hiệu chuẩn và số dư.
Công thức cho trong 6.4.2 dẫn đến:
a) N = 10, K = 4
b) ![]()
c) zi. như cho trong Bảng 6
d) ![]()
e) WSSE = 0,003 4
f) ![]()
g) ![]()
h) ![]()
Hàm hiệu chuẩn là
![]()
Giá trị khớp ![]() thu được bằng cách thay x trong công thức này bằng giá trị NIST xn. Các giá trị khớp này được liệt kê trong Bảng 7.
thu được bằng cách thay x trong công thức này bằng giá trị NIST xn. Các giá trị khớp này được liệt kê trong Bảng 7.
Giá trị khớp có trọng số thu được bằng cách thay x trong công thức
![]()
bằng giá trị NIST xn.
Các số dư có trọng số thu được là
![]()
Các số dư có trọng số này được liệt kê trong Bảng 7.
Bảng 6 – Giá trị của zi.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
zi. |
1,017 |
1,010 |
1,108 |
1,017 |
1,045 |
1,009 |
1,037 |
1,073 |
1,024 |
1,014 |
Bảng 7 – Hiệu chuẩn tuyến tính với giả định độ lệch chuẩn dư tỷ lệ
|
Giá trị NIST xn μm |
Giá trị khớp
μm |
Giá trị khớp có trọng số
|
Giá trị dư |
|||
|
un1 |
un2 |
un3 |
un4 |
|||
|
6,19 9,17 1,99 7,77 4,00 10,77 4,78 2,99 6,98 9,98 |
6,344 9 9,280 7 2,207 4 7,901 5 4,187 5 10,856 9 4,955 9 3,192 5 7,123 2 10,078 6 |
1,025 0 1,012 1 1,109 2 1,016 9 1,046 9 1,008 1 1,036 8 1,067 7 1,020 5 1,009 9 |
-0,005 6 -0,001 2 0,001 3 0,012 7 0,020 6 0,006 8 -0,001 2 0,015 9 0,002 4 0,015 2 |
-0,012 1 -0,007 7 -0,008 7 -0,011 8 -0,009 4 -0,011 8 -0,018 0 -0,007 5 -0,00 76 -0,005 9 |
-0,005 6 0,006 5 0,006 4 0,006 2 -0,009 4 0,005 9 0,009 2 0,005 9 0,008 1 -0,0009 |
-0,010 5 -0,005 5 -0,003 7 -0,007 9 -0,009 4 0,003 1 0,009 2 0,005 9 0,011 0 0,009 2 |
X Lần lặp 1
O Lần lặp 2
Δ Lần lặp 3
* Lần lặp 4
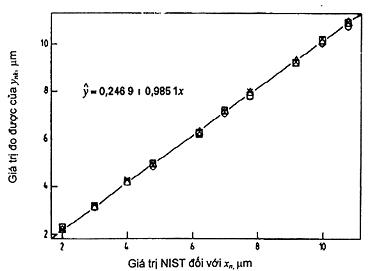
Hình 10 – Đường cong hiệu chuẩn cho khoảng cách dòng với giả định độ lệch chuẩn dư tỷ lệ
Hình 10 thể hiện dữ liệu gốc và hàm hiệu chuẩn với giả định độ lệch chuẩn dư tỷ lệ.
Hình 10, tương tự như Hình 7, chứng minh giả định về tính tuyến tính. Hệ số của hàm hiệu chuẩn tuyến tính có thay đổi một chút so với của Hình 7. Thay đổi này là kết quả của việc ấn định trọng số nhỏ hơn cho giá trị đo được đối với khoảng cách dòng lớn hơn so với giá trị đo được đối với khoảng cách dòng nhỏ (giả định độ lệch chuẩn dư tỷ lệ).
Hình 11 thể hiện đồ thị số dư có trọng số.
Số dư có trọng số cho trên Hình 11 có dạng phân bố ngẫu nhiên. Phân bố tăng của các số dư ở Hình 8 đã mất đi, cho thêm sự tin tưởng vào giả định độ lệch chuẩn dư tỷ lệ. Như trên Hình 8, Hình 11 thể hiện các giá trị dư có trọng số thấp hơn đối với lần lặp 2.
X Lần lặp 1
O Lần lặp 2
Δ Lần lặp 3
* Lần lặp 4
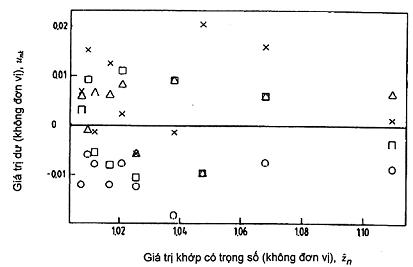
Hình 11 – Số dư có trọng số theo giá trị khớp có trọng số cho khoảng cách dòng với giả định độ lệch chuẩn dư tỷ lệ
9.2.6. Đánh giá sự không khớp của hàm hiệu chuẩn
Bảng 8 thể hiện bảng ANOVA theo mô hình độ lệch chuẩn dư tỷ lệ cho trong 6.5.3.
Bảng ANOVA cho thấy rằng độ biến động của các số dư cho sự không khớp (![]() ) nhỏ hơn so với độ biến động của dữ liệu do sai số thuần túy (
) nhỏ hơn so với độ biến động của dữ liệu do sai số thuần túy (![]() ). Tỷ số
). Tỷ số ![]() nhỏ hơn so với giá trị F0,95(8,30) bằng 2,27. Điều này khẳng định rằng giả định về tính tuyến tính là phù hợp cho thực nghiệm hiệu chuẩn mô tả trong ví dụ này.
nhỏ hơn so với giá trị F0,95(8,30) bằng 2,27. Điều này khẳng định rằng giả định về tính tuyến tính là phù hợp cho thực nghiệm hiệu chuẩn mô tả trong ví dụ này.
Bảng 8 – Bảng ANOVA để so sánh sự không khớp và sai số thuần túy đối với khoảng cách dòng với giả định là độ lệch chuẩn dư tỷ lệ
|
Nguồn |
Bậc tự do, DF |
Tổng bình phương, SS |
SS/DF |
Tỷ số F |
|
Hàm hiệu chuẩn
|
1
|
WSSR = 0,036 9
|
MRS = 0,036 9
|
|
|
Tổng |
39 |
WSST = 0,040 3 |
|
|
9.2.7. Chuyển đổi phép đo sau này
Dựa trên hàm hiệu chuẩn thu được ở 6.4, phép đo trên khoảng cách dòng chưa biết sẽ được chuyển đổi như sau:
a) một phép đo y0 khoảng cách dòng chưa biết sẽ đến giá trị khoảng cách dòng báo cáo là
![]()
b) nhiều phép đo y01, y02, …, y0p khoảng cách dòng chưa biết sẽ dẫn đến giá trị khoảng cách dòng báo cáo là
![]()
9.3. Phương pháp kiểm soát
9.3.1. Cơ sở và dữ liệu
Hai khoảng cách dòng được chọn cho phương pháp kiểm soát này (m = 2). Các khoảng cách dòng này được chọn sao cho bao trùm càng rộng càng tốt dãy giá trị gặp phải trong điều kiện hoạt động bình thường. Mỗi khoảng cách dòng được đo hàng ngày. Bảng 9 thể hiện các phép đo thu được trong 7 ngày đầu tiên, cùng với giá trị NIST xi.
9.3.2. Tính giới hạn kiểm soát trên và dưới
Giá trị 0,05 được chọn cho α. Từ 6.4.2, ta có
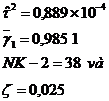
Giá trị này dẫn đến:
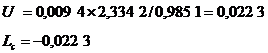
Các giới hạn này được vẽ đồ thị ở Hình 12.
Bảng 9 – Dữ liệu thu thập cho phương pháp kiểm soát
|
Ngày |
Giá trị NIST xi μm |
Giá trị đo được yi μm |
Giá trị chuyển đổi
|
Giá trị kiểm soát ci |
|
1
2
3
4
5
6
7 |
2,99 10,77 2,99 10,77 2,99 10,77 2,99 10,77 2,99 10,77 2,99 10,77 2,99 10,77 |
3,154 10,760 3,215 10,909 3,165 10,740 3,213 10,892 3,179 10,772 3,198 10,807 3,230 10,897 |
2,951 10,673 3,013 10,823 2,962 10,652 3,011 10,806 2,976 10,685 2,996 10,720 3,028 10,811 |
-0,013 -0,009 0,008 0,005 -0,009 -0,011 0,007 0,003 -0,005 -0,008 0,002 -0,005 0,013 0,004 |
9.3.3. Chuyển đổi và vẽ đồ thị dữ liệu
a) Các giá trị yi được chuyển đổi thành ![]() sử dụng hàm hiệu chuẩn và các giá trị kiểm soát
sử dụng hàm hiệu chuẩn và các giá trị kiểm soát
![]()
thu được. Mô hình với độ lệch chuẩn dư tỷ lệ được chấp nhận để rút ra hàm hiệu chuẩn, phương pháp kiểm soát sử dụng các hiệu được chuẩn hóa làm giá trị kiểm soát chứ không phải là hiệu thông thường (![]() ). Giá trị kiểm soát được liệt kê trong Bảng 9.
). Giá trị kiểm soát được liệt kê trong Bảng 9.
b) Các giá trị kiểm soát được vẽ trên biểu đồ kiểm soát (Hình 12).
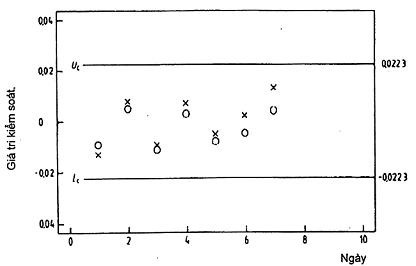
CHÚ DẪN: x = RM với giá trị thấp, o = RM với giá trị cao
Hình 12 – Biểu đồ kiểm soát để xác nhận hiệu lực của đường cong hiệu chuẩn dùng cho khoảng cách dòng với giả định độ lệch chuẩn dư tỷ lệ
9.3.4. Quyết định về tình trạng của hệ thống
Hệ thống có vẻ nằm trong tầm kiểm soát và hàm hiệu chuẩn không cần phải cập nhật cho tới ngày thứ 7.
9.3.5. Ước lượng độ không đảm bảo của giá trị chuyển đổi trong quá trình xác nhận hiệu lực của hàm hiệu chuẩn
Vì chỉ sử dụng hai RM trong biểu đồ kiểm soát nên tất cả các giá trị kiểm soát ci đều được đưa vào tính toán ước lượng hệ số biến động của giá trị chuyển đổi. Ước lượng này bằng
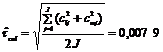
Với 2J = 14 bậc tự do.
Khoảng tin cậy gần đúng với giá trị thực chưa biết của đại lượng ước lượng bởi giá trị chuyển đổi ![]() với mức tin cậy 0,95 thu được là
với mức tin cậy 0,95 thu được là
![]()
PHỤ LỤC A
(quy định)
Danh mục các ký hiệu và chữ viết tắt
N Số mẫu chuẩn
K hoặc Kn Số phép đo lặp trên một mẫu chuẩn
NK Tổng số phép đo trên tất cả các mẫu chuẩn
x Giá trị chấp nhận của mẫu chuẩn
xb Giá trị chấp nhận của mẫu trắng
![]() Trung bình của tất cả các giá trị chấp nhận
Trung bình của tất cả các giá trị chấp nhận
![]() Nghịch đảo của giá trị chấp nhận của mẫu chuẩn (1/x)
Nghịch đảo của giá trị chấp nhận của mẫu chuẩn (1/x)
![]() Trung bình của tất cả các giá trị chấp nhận nghịch đảo
Trung bình của tất cả các giá trị chấp nhận nghịch đảo
y Phép đo mẫu chuẩn
yb Phép đo mẫu trắng
![]() Trung bình của tất cả các phép đo
Trung bình của tất cả các phép đo
y. Trung bình các phép đo của mẫu chuẩn cụ thể
z Tỷ số các phép đo của RM cụ thể trên giá trị chấp nhận của RM đó (y/x)
![]() Phần chặn của hàm hiệu chuẩn với giả định độ lệch chuẩn dư không đổi
Phần chặn của hàm hiệu chuẩn với giả định độ lệch chuẩn dư không đổi
![]() Độ dốc của hàm hiệu chuẩn với giả định độ lệch chuẩn dư không đổi
Độ dốc của hàm hiệu chuẩn với giả định độ lệch chuẩn dư không đổi
![]() Phần chặn của hàm hiệu chuẩn với giả định độ lệch chuẩn dư tỷ lệ
Phần chặn của hàm hiệu chuẩn với giả định độ lệch chuẩn dư tỷ lệ
![]() Độ dốc của hàm hiệu chuẩn với giả định độ lệch chuẩn dư tỷ lệ
Độ dốc của hàm hiệu chuẩn với giả định độ lệch chuẩn dư tỷ lệ
![]() Độ lệch giữa phép đo và giá trị mong đợi với giả định về tuyến tính và độ lệch chuẩn dư không đổi
Độ lệch giữa phép đo và giá trị mong đợi với giả định về tuyến tính và độ lệch chuẩn dư không đổi
![]() Độ lệch giữa phép đo và giá trị mong đợi với giả định về tính tuyến tính và độ lệch chuẩn dư tỷ lệ
Độ lệch giữa phép đo và giá trị mong đợi với giả định về tính tuyến tính và độ lệch chuẩn dư tỷ lệ
e Số dư với giả định về tính tuyến tính và độ lệch chuẩn dư không đổi
u Số dư có trọng số với giả định về tính tuyến tính và độ lệch chuẩn dư tỷ lệ
![]() Phương sai dư không đổi (phương sai của
Phương sai dư không đổi (phương sai của ![]() )
)
![]() Phương sai đi kèm với sai số thuần túy với giả định độ lệch chuẩn dư không đổi
Phương sai đi kèm với sai số thuần túy với giả định độ lệch chuẩn dư không đổi
![]() Phương sai đi kèm với sự không khớp với giả định độ lệch chuẩn dư không đổi
Phương sai đi kèm với sự không khớp với giả định độ lệch chuẩn dư không đổi
![]() Phương sai dư tỷ lệ (phương sai của
Phương sai dư tỷ lệ (phương sai của ![]() )
)
![]() Phương sai đi kèm với sai số thuần túy với giả định độ lệch chuẩn dư tỷ lệ
Phương sai đi kèm với sai số thuần túy với giả định độ lệch chuẩn dư tỷ lệ
![]() Phương sai đi kèm với sự không khớp với giả định độ lệch chuẩn dư tỷ lệ
Phương sai đi kèm với sự không khớp với giả định độ lệch chuẩn dư tỷ lệ
SSE Tổng các số dư bình phương e
WSSE Tổng các số dư trọng số bình phương u
SST, WSST Tổng toàn các độ lệch bình phương với giả định độ lệch chuẩn dư không đổi hay tỷ lệ, tương ứng
SSP, WSSP Tổng các độ lệch bình phương do sai số thuần túy với giả định độ lệch chuẩn dư không đổi hay tỷ lệ, tương ứng
SSR, WSSR Tổng các độ lệch bình phương giải thích theo hàm hiệu chuẩn với giả định độ lệch chuẩn dư không đổi hay tỷ lệ, tương ứng
![]() Mức ý nghĩa
Mức ý nghĩa
![]() Mức tin cậy
Mức tin cậy
![]() Phân vị
Phân vị ![]() của phân bố F với
của phân bố F với ![]() và
và ![]() bậc tự do
bậc tự do
![]() Phân vị
Phân vị ![]() của phân bố t với n1 bậc tự do
của phân bố t với n1 bậc tự do
Ud Giới hạn kiểm soát trên với giả định độ lệch chuẩn dư không đổi
Ld Giới hạn kiểm soát dưới với giả định độ lệch chuẩn dư không đổi
Uc Giới hạn kiểm soát trên với giả định độ lệch chuẩn dư tỷ lệ
Lc Giới hạn kiểm soát dưới với giả định độ lệch chuẩn dư tỷ lệ
d Giới hạn kiểm soát với giả định độ lệch chuẩn dư không đổi
c Giới hạn kiểm soát với giả định độ lệch chuẩn dư tỷ lệ
PHỤ LỤC B
(quy định)
Phương pháp cơ bản khi số lần lặp không phải là hằng số
Khi số lần lặp đối với mỗi RM, Kn không phải là hằng số, hàm hiệu chuẩn vẫn có thể được ước lượng bằng cách điều chỉnh công thức trong 6.2.2, 6.4.2 và 6.5.
B.1. Các ước lượng của ![]() và
và ![]() được tính như sau:
được tính như sau:
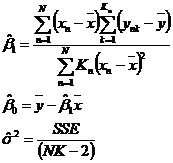
Trong đó
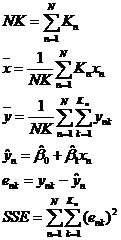
B.2. Các ước lượng của ![]() và
và ![]() được tính như sau:
được tính như sau:

Trong đó
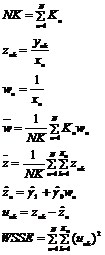
B.3. Tính không khớp được đánh giá như dưới đây. Các Bảng 1 và 2 vẫn áp dụng, trong đó
![]()
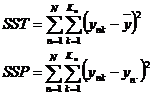
SSE như được xác định ở B.1
và
![]()
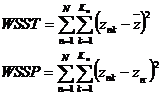
WSSE như được xác định ở B.2
PHỤ LỤC C
(tham khảo)
THƯ MỤC TÀI LIỆU THAM KHẢO
[1] MANDEL, J. Fitting straight lines when both variables are in error, Journal of Quality Technology, 16 (No.1), 1984, pp. 1-14 (Đường thẳng khớp khi cả hai biến cố có sai số, Báo công nghệ chất lượng).
[2] GRAYBILL, F. Theory and applications of the Linear Model, Duxbury Press, North Scituate, MA, 1976 (Lý thuyết và ứng dụng mô hình tuyến tính).
[3] DRAPER, N. and SMITH, H. Applied Regression Analysis, 2nd edn. Wiley, New York, 1981 (Phân tích hồi quy ứng dụng).
[4] CARROLL, R., SPIEGELMAN, C. and SACKS, J. A quick and easy multiple-use calibration curve procedure, Technometrics, 30, 1988, phương pháp. 137-141 (Quy trình đường cong hiệu chuẩn đa ứng dụng nhanh chóng và dễ dàng).
[5] MEE, R., EBERHARDT, K. and REEVE, C. Calibration and simultaneous tolerance intervals for regression, Technometrics, 23, 1991, phương pháp. 211-219 (Khoảng hiệu chuẩn và dung sai đồng thời cho hồi quy).
[6] ISO 7870:1993, Control charts – General guide and introduction (Biểu đồ kiểm soát – Hướng dẫn và giới thiệu chung)
[7] ISO 8258:1991, Shewhart control charts (Biểu đồ kiểm soát Shewhart)
[8] CROARKIN, C. and VARNER, R. Measurement assurance for dimensional measurements on integrated-circuits photomasks. NSB Technical Note 1164, 1982 (Đảm bảo đo lường cho các phép đo kích thước trên mạng che quang mạch tích hợp).
MỤC LỤC
Lời nói đầu
Lời giới thiệu
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Thuật ngữ và định nghĩa
4. Nguyên tắc chung
5. Phương pháp cơ bản
5.1. Khái quát
5.2. Giả định
5.3. Thực nghiệm hiệu chuẩn
5.4. Chiến lược phân tích dữ liệu
6. Các bước của phương pháp cơ bản
6.1. Vẽ đồ thị dữ liệu thu thập trong quá trình thực nghiệm hiệu chuẩn
6.2. Ước lượng hàm hiệu chuẩn tuyến tính với giả định độ lệch chuẩn dư không đổi
6.3. Đồ thị hàm hiệu chuẩn và các số dư
6.4. Ước lượng hàm hiệu chuẩn với giả định độ lệch chuẩn dư tỷ lệ và đồ thị hàm hiệu chuẩn và số dư
6.5. Đánh giá sự không khớp của hàm hiệu chuẩn
6.6. Chuyển đổi các giá trị đo sau này với hàm hiệu chuẩn
7. Phương pháp kiểm soát
7.1. Khái quát
7.2. Tính giới hạn kiểm soát trên và dưới
7.3. Tập hợp và vẽ đồ thị dữ liệu
7.4. Quyết định về tình trạng của hệ thống
7.5. Ước lượng độ không đảm bảo của giá trị chuyển đổi
8. Hai lựa chọn phương pháp cơ bản
8.1. Khái quát
8.2. Phương pháp hiệu chuẩn một điểm
8.3. Kỹ thuật đóng khung
9. Ví dụ
9.1. Khái quát
9.2. Phương pháp cơ bản
9.3. Phương pháp kiểm soát
Phụ lục A (quy định), Danh mục các ký hiệu và chữ viết tắt
Phụ lục B (tham khảo), Phương pháp cơ bản khi số lần lặp không phải là hằng số
Phụ lục C (tham khảo), Thư mục tài liệu tham khảo
1) Tiêu chuẩn này hiện đã được thay thế bằng ISO 3534-1:2006 và được chấp nhận thành TCVN 8244-1:2010
2) Tiêu chuẩn này hiện đã được thay thế bằng ISO 3534-1:2006 và được chấp nhận thành TCVN 8244-2:2010