Nội dung toàn văn Tiêu chuẩn quốc gia TCVN 9945-4:2013 (ISO 7870-4:2011) về Biểu đồ kiểm soát – Phần 4: Biểu đồ tổng tích lũy
TIÊU CHUẨN QUỐC GIA
TCVN 9945-4:2013
ISO 7870-4:2011
BIỂU ĐỒ KIỂM SOÁT – PHẦN 4: BIỂU ĐỒ TỔNG TÍCH LŨY
Control charts – Part 4: Cumulative sum charts
Lời nói đầu
TCVN 9945-4:2013 hoàn toàn tương đương với ISO 7870-4:2011;
TCVN 9945-4:2013 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Bộ tiêu chuẩn TCVN 9945, chấp nhận bộ tiêu chuẩn ISO 7870, gồm các phần dưới đây có tên chung “Biểu đồ kiểm soát”:
– TCVN 9945-1:2013 (ISO 7870-1:2007), Phần 1: Hướng dẫn chung
– TCVN 9945-2:2013 (ISO 7870-2:2013), Phần 2: Biểu đồ kiểm soát Shewhart
– TCVN 9945-3:2013 (ISO 7870-3:2012), Phần 3: Biểu đồ kiểm soát chấp nhận
– TCVN 9945-4:2013 (ISO 7870-4:2011), Phần 4: Biểu đồ tổng tích lũy
Lời giới thiệu
Tiêu chuẩn này thể hiện tính linh hoạt và hữu ích của phương pháp trực quan rất đơn giản nhưng có hiệu lực trong giải thích các dữ liệu được sắp xếp theo mọi trình tự có ý nghĩa. Những dữ liệu này có thể từ số hiệu kinh doanh tổng thể như doanh thu, lợi nhuận hoặc tổng chi phí đến dữ liệu hoạt động chi tiết như là thiếu hàng và thiếu kiểm soát các tham số quá trình riêng lẻ và các đặc trưng sản phẩm. Dữ liệu cũng có thể được thể hiện theo dãy các giá trị riêng lẻ theo thang đo liên tục (ví dụ: 24,60, 31,21, 18,97…), theo dạng thức “có/không”, “tốt”/“xấu”, “thành công”/ “thất bại” hoặc theo thước đo tổng hợp (ví dụ: trung bình, độ rộng, số đếm các biến cố).
Phương pháp có tên hơi đặc biệt là tổng tích lũy hoặc viết tắt là “cusum”. Tên gọi này liên quan đến quá trình trừ đi giá trị được xác định trước, ví dụ: giá trị đích, giá trị ưu tiên hoặc giá trị quy chiếu từ mỗi quan trắc theo trình tự và tích lũy dần (nghĩa là cộng) các hiệu số. Đồ thị chuỗi các hiệu số tích lũy được gọi là biểu đồ cusum. Quá trình toán học đơn giản này có ảnh hưởng lớn đến việc giải thích trực quan dữ liệu như sẽ được minh họa.
Phương pháp cusum đã được những người chơi gôn vô tình sử dụng trên toàn thế giới. Bằng cách cho điểm một lượt chơi là “cộng” 4, hoặc có thể là “trừ” 2, người chơi gôn đang sử dụng phương pháp cusum theo phương diện số. Họ trừ đi giá trị “gậy chuẩn” từ điểm số thực tế của mình và cộng (tích lũy) các hiệu thu được. Đây là phương pháp cusum trong thực tế. Tuy nhiên, phương pháp này chưa được biết đến rộng rãi và do đó là công cụ ít được dùng trong kinh doanh, công nghiệp, thương mại và dịch vụ công cộng. Điều này có thể do các phương pháp cusum thường được trình bày bằng ngôn ngữ thống kê hơn là ngôn ngữ ở nơi làm việc.
Mục đích của tiêu chuẩn này là giúp những người sử dụng tiềm năng có thể dễ dàng thông hiểu, tạo điều kiện trao đổi thông tin rộng rãi và hiểu biết về phương pháp. Phương pháp này có ưu điểm hơn biểu đồ Schewhart thường thấy là phương pháp cusum phát hiện sự thay đổi với lượng quan trọng nhanh hơn gấp ba lần. Ngoài ra, như trong môn đánh gôn, khi đích thay đổi theo mỗi lỗ, đồ thị cusum không bị ảnh hưởng, không giống như biểu đồ Schewhart chuẩn khi đường kiểm soát đòi hỏi điều chỉnh liên tục.
Ngoài biểu đồ Schewhart, có thể sử dụng biểu đồ EW MA (trung bình trượt có trọng số mũ). Mỗi điểm vẽ trên biểu đồ EW MA kết hợp thông tin từ tất cả các nhóm con hoặc các quan trắc trước đó nhưng đưa ra trọng số nhỏ hơn cho dữ liệu quá trình vì chúng trở nên “cũ hơn” theo trọng số phân rã hàm mũ. Theo cách tương tự với biểu đồ cusum, biểu đồ EW MA có thể nhạy trong việc phát hiện mọi mức độ dịch chuyển trong quá trình. Vấn đề này được thảo luận nhiều hơn trong các tiêu chuẩn khác thuộc bộ này.
BIỂU ĐỒ KIỂM SOÁT – PHẦN 4: BIỂU ĐỒ TỔNG TÍCH LŨY
Control charts – Part 4: Cumulative sum charts
1. Phạm vi áp dụng
Tiêu chuẩn này đưa ra các quy trình thống kê để thiết lập chương trình tổng tích lũy (cusum) đối với kiểm soát quá trình và kiểm soát chất lượng bằng cách sử dụng dữ liệu định lượng (đo được) và dữ liệu định tính. Tiêu chuẩn này mô tả các phương pháp có mục đích chung là ra quyết định bằng cách sử dụng các kỹ thuật tổng tích lũy (cusum) cho việc theo dõi, kiểm soát và phân tích quá khứ.
2. Tài liệu viện dẫn
Các tài liệu viện dẫn dưới đây rất cần thiết cho việc áp dụng tiêu chuẩn này. Đối với các tài liệu ghi năm công bố thì áp dụng bản được nêu. Đối với các tài liệu không ghi năm công bố thì áp dụng bản mới nhất, bao gồm cả các sửa đổi.
TCVN 8244-1 (ISO 3534-1), Thống kê học – Từ vựng và ký hiệu – Phần 1: Thuật ngữ chung về thống kê và thuật ngữ dùng trong xác suất
TCVN 8244-2(ISO 3534-2), Thống kê học – Từ vựng và ký hiệu – Phần 2: Thống kê ứng dụng
3. Thuật ngữ và định nghĩa, chữ viết tắt và ký hiệu
Tiêu chuẩn này sử dụng các thuật ngữ và định nghĩa nêu trong TCVN 8244-1 (ISO 3534-1), TCVN 8244-2 (ISO 3534-2) và các thuật ngữ, định nghĩa dưới đây:
3.1. Thuật ngữ và định nghĩa
3.1.1. Giá trị đích (target value)
T
Giá trị trong đó việc phát hiện sự sai lệch so với mức trung bình là cần thiết.
CHÚ THÍCH 1: Với cusum được vẽ biểu đồ, sai lệch so với giá trị đích được cộng dồn.
CHÚ THÍCH 2: Sử dụng mặt nạ “V”, giá trị đích thường được gọi là giá trị quy chiếu hoặc giá trị kiểm soát danh nghĩa. Nếu vậy, cần thừa nhận rằng đó không nhất thiết là giá trị mong muốn hoặc ưu tiên nhất, như có thể đề cập trong các tiêu chuẩn khác. Nó chỉ đơn giản là giá trị đích thích hợp cho việc xây dựng biểu đồ cusum.
3.1.2. Giá trị mốc (datum value)
Giá trị ácusum lập bảngñ từ đó tính các hiệu.
CHÚ THÍCH: Giá trị mốc trên là T + fse, để theo dõi độ dịch chuyển trên. Giá trị mốc dưới là T – fse, để theo dõi độ dịch chuyển dưới.
3.1.3. Độ dịch chuyển quy chiếu (reference shift)
F, ¦
ácusum theo bảngñ Hiệu giữa giá trị đích (3.1.1) và giá trị mốc (3.1.2)
CHÚ THÍCH: Cần phân biệt giữa ¦ liên quan đến độ dịch chuyển quy chiếu chuẩn hóa với F là độ dịch chuyển quy chiếu quan trắc, F = ¦se
3.1.4. Độ dịch chuyển quy chiếu (reference shift)
F, ¦
ámặt nạ V cắt tỉañ Đường dốc của cạnh mặt nạ (đường tiếp tuyến của góc mặt nạ).
CHÚ THÍCH: Cần phân biệt giữa f liên quan đến độ dịch chuyển quy chiếu chuẩn hóa với F là độ dịch chuyển quy chiếu quan trắc, F = ¦se.
3.1.5. Khoảng quyết định (decision interval)
H, h
Tổng tích lũy ácusum theo bảngñ của sai lệch so với giá trị mốc (3.1.2) cần thiết để gây ra báo hiệu.
CHÚ THÍCH: Cần phân biệt giữa h liên quan đến khoảng quyết định chuẩn hóa với H là khoảng quyết định quan trắc, H = hse.
3.1.6. Khoảng quyết định (decision interval)
H, h
Nửa chiều cao ámặt nạ V cắt tỉañ tại điểm mốc của mặt nạ.
CHÚ THÍCH: Cần phân biệt giữa h liên quan đến khoảng quyết định chuẩn hóa với H là khoảng quyết định quan trắc, H = hse.
3.1.7. Độ dài trung bình của loạt mẫu (average run length)
L
Số lượng mẫu trung bình được lấy đến điểm tại đó xuất hiện báo hiệu.
CHÚ THÍCH: Độ dài trung bình của loạt mẫu (L) thường liên quan đến mức quá trình cụ thể trong đó nó có chỉ số dưới thích hợp, ví dụ, L0, có nghĩa là độ dài trung bình của loạt mẫu khi quá trình ở mức đích, nghĩa là dịch chuyển bằng “không”.
3.2. Chữ viết tắt
ARL độ dài trung bình của loạt mẫu
CS1 chương trình cusum với ARL dài ở dịch chuyển bằng “không”
CS2 chương trình cusum với ARL ngắn hơn ở dịch chuyển bằng “không”
DI khoảng quyết định
EWMA trung bình trượt có trọng số mũ
FIR đáp ứng ban đầu nhanh
LCL giới hạn kiểm soát dưới
RV giá trị quy chiếu
UCL giới hạn kiểm soát trên
3.3. Ký hiệu
a hệ số tỷ lệ
C giá trị cusum
Cr hiệu giá trị cusum giữa điểm dẫn và điểm mất kiểm soát
c4 hệ số ước lượng độ lệch chuẩn trong nhóm con
d lượng thay đổi được phát hiện
D lượng thay đổi chuẩn hóa được phát hiện
d khoảng cách dẫn
d2 hệ số ước lượng độ lệch chuẩn trong nhóm con so với độ rộng trong nhóm con
F độ dịch chuyển quy chiếu quan trắc
¦ độ dịch chuyển quy chiếu chuẩn hóa
H khoảng quyết định quan trắc
H khoảng quyết định chuẩn hóa
J chỉ số
j cỡ điều chỉnh quá trình
K giá trị mốc cusum đối với dữ liệu rời rạc
k số nhóm con
L0 độ dài trung bình của loạt mẫu tại dịch chuyển bằng “không”
Ld độ dài trung bình của loạt mẫu tại độ dịch chuyển d
m giá trị trung bình tổng thể
m số đếm trung bình
n cỡ nhóm con
p xác suất “thành công”
![]() độ rộng nhóm con trung bình
độ rộng nhóm con trung bình
r số điểm được vẽ giữa điểm dẫn và điểm mất kiểm soát
s độ lệch chuẩn quá trình
s độ lệch chuẩn trong nhóm con
![]() độ lệch chuẩn trong nhóm con ước lượng
độ lệch chuẩn trong nhóm con ước lượng
se sai số chuẩn
s độ lệch chuẩn trong nhóm con quan trắc
![]() độ lệch chuẩn nhóm con trung bình
độ lệch chuẩn nhóm con trung bình
![]() sai số chuẩn trung bình thừa nhận từ k nhóm con
sai số chuẩn trung bình thừa nhận từ k nhóm con
T giá trị đích
Tm tỷ lệ xuất hiện quy chiếu hay tỷ lệ đích
Tp tỷ lệ quy chiếu hay tỷ lệ đích
t điểm thay đổi thực
t điểm thay đổi quan trắc
Vavg điện áp trung bình
![]() điện áp trung bình ước lượng
điện áp trung bình ước lượng
w chênh lệch giữa các giá trị trung bình nhóm con liên tiếp
x kết quả riêng rẽ
![]() giá trị trung bình cộng (của nhóm con)
giá trị trung bình cộng (của nhóm con)
![]() trung bình của trung bình nhóm con
trung bình của trung bình nhóm con
4. Đặc điểm chính của biểu đồ tổng tích lũy (cusum)
Biểu đồ cusum là tổng các sai lệch so với một giá trị quy chiếu được chọn trước nào đó. Trung bình của mọi nhóm giá trị liên tiếp được thể hiện trực quan bằng đường dốc hiện tại của đồ thị. Đặc điểm chính của biểu đồ cusum được nêu dưới đây:
a) Nhạy trong việc phát hiện các thay đổi về trung bình.
b) Bất kỳ sự thay đổi nào về trung bình và mức độ thay đổi đều được thể hiện trực quan bằng sự thay đổi đường dốc trên đồ thị:
1) đồ thị nằm ngang cho biết giá trị “tại đích” hoặc giá trị quy chiếu;
2) đường dốc đi xuống cho biết trung bình thấp hơn giá trị quy chiếu hoặc giá trị đích: đường càng dốc thì khác biệt càng lớn;
3) đường dốc đi lên cho biết trung bình lớn hơn giá trị quy chiếu hoặc giá trị đích; đường càng dốc thì khác biệt càng lớn;
c) Có thể sử dụng cho mục đích điều tra quá khứ, trên cơ sở vận hành cho kiểm soát, và dự đoán hiệu năng trong tương lai gần.
Đối với điểm b) trên, biểu đồ cusum có khả năng chỉ thị rõ các điểm thay đổi; chúng được biểu thị rõ bằng sự thay đổi độ dốc của đồ thị cusum. Điều này có lợi ích rất lớn đối với quản lý quá trình: có thể xác định nhanh chóng và chính xác thời điểm quá trình thay đổi để có thể thực hiện hành động khắc phục thích hợp.
Một đặc điểm rất hữu ích khác của hệ thống cusum là nó có thể được xử lý mà không cần vẽ đồ thị, nghĩa là dưới dạng bảng. Điều này rất hữu ích nếu hệ thống được sử dụng để theo dõi quá trình kỹ thuật cao, ví dụ: hãng sản xuất phim nhựa, trong đó số lượng tham số quá trình và đặc trưng của sản phẩm rất lớn. Dữ liệu từ quá trình đó có thể được chụp tự động, tải về phần mềm cusum để đưa ra phân tích cusum tự động. Sau đó người quản lý quá trình có thể được cảnh báo về những thay đổi đối với nhiều đặc trưng đồng thời. Phụ lục B đưa ra ví dụ về phương pháp này.
5. Các bước cơ bản trong xây dựng biểu đồ cusum – Trình bày bằng đồ thị
Sử dụng các bước sau đây để lập biểu đồ cusum cho các giá trị riêng lẻ.
Bước 1: Chọn giá trị quy chiếu, đích, kiểm soát hoặc giá trị ưu tiên. Trung bình của các kết quả trước đó thường sẽ đưa ra sự phân biệt tốt.
Bước 2: Lập bảng kết quả theo trình tự có ý nghĩa (ví dụ: thời gian). Trừ đi giá trị quy chiếu từ mỗi kết quả.
Bước 3: Cộng dồn các giá trị thu được trong Bước 2. Sau đó vẽ đồ thị tổng này như trên biểu đồ cusum.
Bước 4: Để có được những hiệu ứng trực quan tốt nhất, lập thang hoành độ giữa các điểm vẽ đồ thị không rộng hơn khoảng 2,5 mm.
Bước 5: Để có sự phân biệt hợp lý, mà không cần độ nhạy quá mức, các tùy chọn sau đây được khuyến nghị:
a) chọn khoảng vẽ đồ thị thích hợp cho trục hoành và lấy khoảng tương tự trên trục tung bằng 2s (hoặc 2se nếu cusum trung bình được vẽ biểu đồ), làm tròn số khi thích hợp, hoặc
b) nếu cần phát hiện thay đổi đã biết, là d, chọn thang đo trục tung sao cho tỷ lệ đơn vị thang đo trên thang đo thẳng đứng được chia cho đơn vị thang đo trên thang đo trục hoành là giữa d và 2d, làm tròn số khi thích hợp.
CHÚ THÍCH: Việc lựa chọn thang đo là rất quan trọng vì nếu thang đo không thích hợp sẽ tạo ra ấn tượng do tính chất bất ổn của đồ thị hoặc thấy không có gì thay đổi. Chương trình mô tả trong a) và b) cần đưa ra thang đo cho thấy sự thay đổi một cách hợp lý, không quá nhạy và cũng không quá áp đặt.
6. Ví dụ về đồ thị cusum – Điện áp động cơ
6.1. Quá trình
Giả sử thu được theo trình tự thời gian bộ 40 giá trị của đặc trưng cụ thể. Các giá trị này là điện áp, được lấy theo trình tự sản xuất, trên động cơ công suất nhỏ ở giai đoạn đầu của sản xuất. Nhưng chúng có thể là bất kỳ giá trị riêng lẻ nào được lấy theo trình tự có nghĩa và được thể hiện trên thang đo liên tục. Các giá trị này được thể hiện là:
9, 16, 11, 12, 16, 7, 13, 12, 13, 11, 12, 8, 8, 11, 14, 8, 6, 14, 4, 13, 3, 9, 7, 14, 2, 6, 4, 12, 8, 8, 12, 6, 14, 13, 12, 14, 13, 10, 13, 13.
Giá trị quy chiếu hoặc giá trị điện áp đích là 10 V.
6.2. Đồ thị kết quả đơn giản
Để có được hiểu biết tốt hơn về biểu hiện cơ bản của quá trình, bằng cách xác định các dạng và xu hướng, cách tiếp cận chuẩn đơn giản là vẽ đồ thị những giá trị này theo thứ tự tự nhiên của chúng như thể hiện trên Hình 1 a).
Ngoài việc chỉ ra sự giảm xuống chung ở phần giữa từ điểm khởi đầu cao và với kết thúc cao tương đương, Hình 1 a) không thể hiện rõ vì có tạp lớn, hay có đầu nhọn trong toàn bộ dữ liệu.
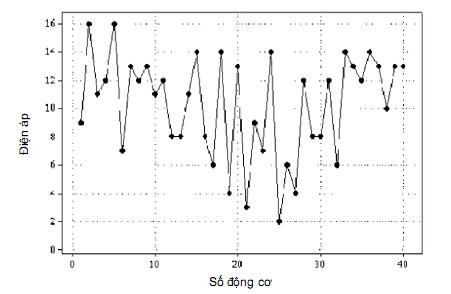
a) Đồ thị đơn giản điện áp động cơ
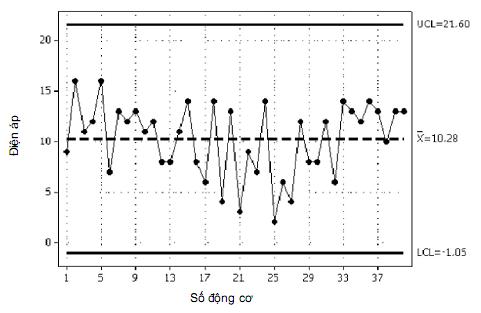
b) Biểu đồ kiểm soát chuẩn đối với các cá thể

c) Biểu đồ cusum
Hình 1 – Ví dụ về điện áp động cơ
6.3. Biểu đồ kiểm soát chuẩn đối với các kết quả riêng lẻ
Mức độ phức tạp tiếp theo là lập biểu đồ kiểm soát chuẩn đối với các cá thể như trong Hình 1 b).
Hình 1 b) thậm chí còn thể hiện ít hơn hình trước đó. Trong thực tế, nó khá sai lầm. Chuẩn mực kiểm soát quá trình thống kê chuẩn để kiểm nghiệm độ ổn định và kiểm soát quá trình là
a) không có điểm nào nằm trên giới hạn kiểm soát trên (UCL) hoặc dưới giới hạn kiểm soát dưới (LCL),
b) không loạt nào trong bảy khoảng hoặc nhiều hơn lên trên hoặc xuống dưới,
c) không loạt nào trong bảy điểm nằm trên hoặc dưới đường tâm.
Câu trả lời đối với tất cả các chuẩn mực này là “không”. Do đó, cần kết luận rằng đây là quá trình ổn định, giá trị “được kiểm soát” quanh giá trị trung bình tổng thể của nó khoảng 10 V, là giá trị đích. Phân tích chuẩn thêm còn cho thấy mặc dù quá trình ổn định, nhưng nó không có khả năng đáp ứng các yêu cầu quy định. Tuy nhiên, bản thân việc phân tích này không đưa ra bất kỳ manh mối nào là vì sao nó không có khả năng đáp ứng các yêu cầu.
Lý do không có khả năng của biểu đồ kiểm soát chuẩn đối với các cá thể có giá trị ở đây là các giới hạn kiểm soát được dựa trên hiệu năng quá trình thực tế chứ không theo các yêu cầu mong muốn hoặc quy định. Do đó, nếu quá trình thể hiện biến động lớn một cách tự nhiên thì các giới hạn kiểm soát cũng lớn theo. Cần có phương pháp tốt hơn cho thấy các kiểu và xu hướng, hay thậm chí xác định chính xác các điểm thay đổi, giúp xác định và loại bỏ các nguồn gây biến động chính.
CHÚ THÍCH: Bằng cách sử dụng các công cụ bổ sung, như biểu đồ cá thể và độ rộng trượt, người thực hành có thể nghiên cứu các vấn đề biến động quá trình khác.
6.4. Biểu đồ cusum – Tổng quan
Một lựa chọn khác được khuyến nghị ở đây là vẽ biểu đồ cusum. Hình 1 c) minh họa đồ thị cusum cho dữ liệu tương tự.
Từ các biểu đồ trước đó, không thấy rõ ngay sự thay đổi quan trọng bất kỳ về mức quá trình xảy ra ở đâu và có xảy ra không, trong khi biểu đồ cusum chỉ rõ dạng thức này. Có thể nhận thấy ngay (bằng mắt) bốn thay đổi về mức quá trình, đó là thay đổi sau động cơ thứ 10, 18 và 31.
Điều 4 cho thấy, đường dốc lên/xuống biểu thị giá trị cao hơn/thấp hơn so với giá trị ưu tiên và đường nằm ngang biểu thị của quá trình theo giá trị ưu tiên đó. Do đó, có thể thấy rằng quá trình này chỉ ở đích trong khoảng thời gian ngắn giữa động cơ 11 và 18. Động cơ 1 đến 10 vận hành cao hơn tương tự với động cơ 33 trở đi, trong khi đó quá trình giữa các động cơ 19 và 32 đã cung cấp cho các động cơ điện áp thấp.
Những thay đổi này và ý nghĩa của chúng được thảo luận và giải thích chi tiết trong 6.6.
Trong tình huống thực tế, bước tiếp theo là tìm ra những gì đã xảy ra tại các điểm sản xuất này gây ra những thay đổi về hiệu năng điện áp. Điều này đặt ra câu hỏi nhất cụ thể nhằm vào việc cải thiện tính nhất quán của hiệu năng ở mức 10 V. Ví dụ, các đặc trưng thiết lập của động cơ 32 khác của động cơ 33 như thế nào? Hay, điều gì xảy ra với hiệu chuẩn thiết bị kiểm tra tại điểm này? Điều này có tương ứng với độ dịch chuyển, bố trí nhân viên hay thay đổi lô không? v.v…. Theo cách này, cho dù tình huống thế nào thì biểu đồ cusum vẫn là công cụ chẩn đoán tuyệt vời. Nó chỉ ra các cơ hội cải tiến.
6.5. Xây dựng biểu đồ cusum
Xây dựng biểu đồ cusum bằng cách sử dụng các giá trị riêng lẻ, như trong ví dụ này, dựa trên các bước rất đơn giản nêu trong Điều 5.
Bước 1: Chọn giá trị quy chiếu, RV. Ở đây giá trị ưu tiên hoặc giá trị quy chiếu được cho là 10 V.
Bước 2: Lập bảng kết quả (điện áp) theo trình tự sản xuất theo số động cơ như trong Bảng 1, cột 2 (và 6). Trừ đi giá trị quy chiếu là 10 từ mỗi kết quả như trong Bảng 1, cột 3 (và 7).
Bước 3: Cộng dồn các giá trị của Bảng 1, cột 3 (và 7) trong cột 4 (và 8). Vẽ đồ thị cột 4 (và 8) theo số (động cơ) quan trắc như trong Hình 1 c), cần lưu ý các bình luận về thang đo trong Bước 4 và 5.
Bảng 1 – Sắp xếp dạng bảng để tính giá trị cusum từ trình tự các giá trị riêng lẻ
|
(1) Số động cơ |
(2) Điện áp |
(3) Điện áp -10 |
(4) Cusum |
(5) Số động cơ |
(6) Điện áp |
(7) Điện áp -10 |
(8) Cusum |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
9 16 11 12 16 7 13 12 13 1 12 8 8 11 14 8 6 14 4 13 |
-1 +6 +1 +2 +6 -3 +3 +2 +3 +1 +2 -2 -2 +1 +4 -2 -4 +4 -6 +3 |
-1 +5 +6 +8 +14 +11 +14 +16 +19 +20 +22 +20 +18 +19 +23 +21 +17 +21 +15 +18 |
21 22 23 24 25 26 27 28 29 30 21 32 33 34 35 36 37 38 39 40 |
3 9 7 14 2 6 4 12 8 8 12 6 14 13 12 14 13 10 13 13 |
-7 -1 -3 +4 -8 -4 -6 +2 -2 -2 +2 -4 +4 +3 +2 +4 +3 0 +3 +3 |
+11 +10 +7 +11 +3 -1 -7 -5 -7 -9 -7 -11 -7 -11 -7 -4 -2 +2 +5 +5 |
6.6. Giải thích biểu đồ cusum
6.6.1. Giới thiệu
Khi biểu đồ cusum được sử dụng theo phương thức chẩn đoán quá khứ, như trong ví dụ này, thì tốt hơn là không tập trung vào các điểm được vẽ đồ thị mà vẽ số đường thẳng tối thiểu đại diện các đường phù hợp nhất bằng mắt, thông qua dữ liệu như trên Hình 1 c).
Sau đó, phải thận trọng để không giải thích đường dốc của các đường này hoặc vị trí tương đối của chúng so với trục tung, như với các đồ thị dữ liệu thông thường. Cũng cần lưu ý rằng, trục tung không còn đại diện cho điện áp thực tế nữa.
Đường thẳng với đường dốc lên/xuống không chỉ ra mức quá trình tăng lên/giảm xuống, như thông lệ, mà nó không đổi tại giá trị lớn hơn/nhỏ hơn giá trị quy chiếu. Đường dốc càng lớn thì khác biệt càng lớn. Đường nằm ngang chỉ ra mức quá trình không đổi tại giá trị quy chiếu. Lúc này việc giải thích biểu đồ cusum đối với động cơ được thảo luận chi tiết hơn.
6.6.2. Cơ sở giải thích biểu đồ cusum bằng cách sử dụng dữ liệu “không tạp ảo”
Giả sử dãy 18 điện áp động cơ đầu tiên là 10, 10, 10, 13, 13, 13, 10, 10, 10, 9, 9, 9, 10, 10, 10, 8, 8, 8, như được thể hiện trong Bảng 2, cột 2, và giá trị quy chiếu vẫn là 10 V.
Bảng 2 – Dữ liệu động cơ ảo minh họa việc giải thích căn bản của biểu đồ cusum
|
(1) Số động cơ |
(2) Điện áp |
(3) Điện áp – 10 |
(4) Cusum |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
10 10 10 13 13 13 10 10 10 9 9 9 10 10 10 8 8 8 |
0 0 0 +3 +3 +3 0 0 0 -1 -1 -1 0 0 0 -2 -2 -2 |
0 0 0 +3 +6 +9 +9 +9 +9 +8 +7 +6 +6 +6 +6 +4 +2 0 |
Biểu đồ cusum thu được giống như trên Hình 2.

Hình 2 – Biểu đồ cusum của dữ liệu điện áp động cơ ảo để minh họa việc giải thích
Khi so sánh điện áp thực tế của Bảng 2, cột 2 với biểu đồ cusum của Hình 2, ta thấy rằng:
a) các động cơ từ 1 đến 3, từ 7 đến 9 và từ 13 đến 15 đều ở giá trị quy chiếu 10 V và tất cả những động cơ này được thể hiện bằng đường nằm ngang trong biểu đồ cusum. Cũng cần lưu ý rằng vị trí của các đường nằm ngang so với thang đo thẳng đứng không liên quan đến những động cơ thực tế này mà liên quan đến hiệu năng trước đó.
b) các động cơ từ 4 đến 6 ở giá trị cao hơn giá trị quy chiếu, cụ thể là 13 V và những động cơ này được thể hiện trên biểu đồ cusum bằng đường dốc đi lên. Điều này là hiển nhiên vì không có biến động về điện áp giữa các động cơ làm xáo trộn vấn đề. Sau đó nếu có tạp thì phương trình để tính giá trị trung bình trong giai đoạn này từ đường dốc cụ thể là:
|
Điện áp trung bình = Giá trị quy chiếu + |
Giá trị cusum ở cuối đường thẳng – Giá trị cusum ở đầu đường thẳng |
|
Số khoảng quan trắc |
![]()
c) tương tự đối với các động cơ từ 9 đến 12:
![]()
d) và đối với các động cơ từ 16 đến 18:
![]()
Tóm lại, các đường dốc khác nhau trên biểu đồ cusum cho thấy các động cơ:
– từ 1 đến 3, từ 7 đến 9 và từ 13 đến 15, điện áp không đổi tại giá trị là 10;
– từ 4 đến 6, điện áp không đổi nhưng tại giá trị là 13;
– từ 10 đến 12, điện áp không đổi tại giá trị là 9; và
– từ 16 đến 18, điện áp không đổi tại giá trị là 8.
Điều này là hiển nhiên khi tham chiếu lại dữ liệu “không tạp”. Nhưng nó không thể hiện rõ ngay khi đề cập đến dữ liệu “tạp” thực tế trong Bảng 1, các cột 2 đến cột 6.
6.6.3. Giải thích bằng cách sử dụng dữ liệu “thực”
Biểu đồ cusum của Hình 1 c) cho thấy:
a) điện áp trung bình từ số động cơ 1 đến 10 có giá trị cao hơn điện áp quy chiếu. Do đó, giá trị tính toán được cho bởi đường dốc là:
|
Điện áp trung bình = Giá trị quy chiếu + |
Giá trị cusum ở cuối đường thẳng – Giá trị cusum ở đầu đường thẳng |
|
Số khoảng quan trắc |
![]()
b) tương tự đối với các động cơ từ 11 đến 18, điện áp trung bình = 10 vì đường thẳng nằm ngang;
c) đối với các động cơ từ 19 đến 31:
![]()
d) đối với các động cơ từ 32 đến 40:
![]()
Tóm lại, biểu đồ cusum cho phép tính các trung bình trượt trong chu kỳ biến đổi so với hiệu năng thực của quá trình. Điều này thể hiện sự tiến bộ đáng kể so với tiêu chuẩn được xác định trước đây cũng như cách tiếp cận trung bình trượt không linh hoạt thường được sử dụng. Ước lượng các kết quả tóm tắt được đưa ra trong Bảng 3.
Bảng 3 – Điện áp trung bình đối với các động cơ liên quan đến khoảng trung bình trượt biến
|
Động cơ |
Điện áp động cơ trung bình |
|
1 đến 10 |
12,0 |
|
11 đến 18 |
10,0 |
|
19 đến 31 |
7,5 |
|
32 đến 40 |
12,6 |
Thay cho phương pháp tính quan hệ giữa đường dốc cusum và điện áp trung bình này, có thể tính đơn giản trung bình trượt cục bộ cho mỗi phần cấp độ không đổi của biểu đồ cusum.
Ví dụ, đối với các động cơ từ 1 đến 10, bằng cách tính:
![]()
Việc sử dụng điện áp riêng lẻ này đôi khi đưa ra các kết quả hơi khác so với phương pháp đường dốc. Điều này do làm trơn độ biến động cục bộ trong dữ liệu bằng cách đặt đường thẳng qua các điểm cá thể.
6.7. Sơ đồ Manhattan
Với ước lượng các điểm thay đổi về mức điện áp và giá trị của chúng đã được thiết lập, thường sẽ đơn giản hóa hơn và nâng cao lợi thế của việc trình bày trên trục thẳng đứng gốc biểu thị điện áp thực tế đi đến bước trình bày bổ sung dữ liệu dạng “không tạp”. Sự trình bày này được Manhattan lấy ý tưởng từ đường chân trời thẳng và do đó được gọi là sơ đồ Manhattan.
Đây đơn giản là biểu thị các kết quả, cho trong 6.6.3 a), b), c) và d), như đồ thị điện áp thông thường so với dãy động cơ được sản xuất. Điều này được thể hiện trên Hình 3 để so sánh với dữ liệu cusum trong Hình 1 c) và dữ liệu tạp ban đầu trong Hình 1 a).
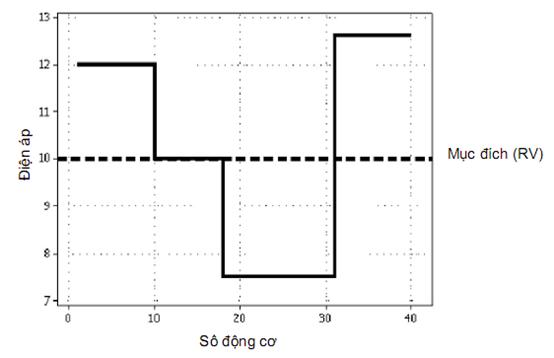
Hình 3 – Đồ thị Manhattan của dữ liệu động cơ
Hình 3, Hình 1 c) và Hình 1 a) tóm tắt vai trò và giá trị của phương pháp cusum theo phương thức nghiên cứu thông qua phân tích hiệu năng quá trình trước đó. Chúng thể hiện những gì có thể đạt được bằng cách sử dụng ngôn ngữ dễ hiểu và các phương pháp nâng cao trực quan đơn giản mà không có sử dụng, hay nhờ đến, ký hiệu toán học hay biểu thức thống kê chính thức.
Vì tính chất đơn giản và rõ ràng của sơ đồ Manhattan, đôi khi sẽ hữu ích khi xem sơ đồ cusum như giai đoạn kỹ thuật trung gian và trình bày đơn giản dữ liệu dưới dạng Manhattan để tạo thuận lợi cho việc trao đổi thông tin phi kỹ thuật, thông hiểu và áp dụng rộng hơn.
7. Quy tắc cơ bản của việc ra quyết định dựa trên cusum
7.1. Nhu cầu đối với các quy tắc quyết định
Quy tắc quyết định có thể cần thiết để hợp lý hóa việc giải thích biểu đồ cusum. Khi quy tắc quyết định thích hợp cho thấy điều đó thì hành động được thực hiện, tùy thuộc vào tính chất của quá trình. Các hành động điển hình là:
a) đối với kiểm soát trong quá trình: điều chỉnh các điều kiện quá trình;
b) trong bối cảnh cải tiến: nghiên cứu nguyên nhân cơ bản của thay đổi; và
c) theo phương thức dự báo: phân tích và, nếu cần, điều chỉnh mô hình dự báo hoặc các tham số của nó.
7.2. Cơ sở ra quyết định
Thiết lập chuẩn mực cơ bản cho việc ra quyết định rõ ràng là một điều kiện thiết yếu.
Thước đo thích hợp định lượng “tạp” trong hệ thống là cần thiết để đưa ra cơ sở hiệu quả cho việc phát hiện báo hiệu. Cái gì thể hiện tạp, và cái gì thể hiện báo hiệu, được xác định bằng chiến lược theo dõi lựa chọn, như thực hiện bao nhiêu quan trắc, tần số như thế nào và cách thức để tạo mẫu hay nhóm con. Ngoài ra, thước đo sử dụng để định lượng độ biến động cũng có thể ảnh hưởng đến vấn đề này.
Độ biến động vốn có thường được đo bằng một trong hai thước đo thống kê dưới đây:
a) Độ lệch chuẩn: khi các quan trắc đơn lẻ là cơ sở để vẽ đồ thị cusum
Các quan trắc đơn lẻ dùng cho việc tính độ lệch chuẩn thường được lấy từ đoạn đồng nhất của dữ liệu quá trình. Sau đó hiệu năng này trở thành chuẩn mực lựa chọn hợp lý hơn để đánh giá. Mọi biến động lớn hơn độ biến động vốn có này được cho là do các nguyên nhân đặc biệt cho thấy sự dịch chuyển về trung bình của chuỗi hay sự thay đổi độ lớn tự nhiên của biến động hoặc cả hai.
b) Sai số chuẩn: khi một hàm số của nhóm con các quan trắc, như trung bình, trung vị hay độ rộng, là cơ sở cho vẽ đồ thị cusum
Khái niệm về phân nhóm là độ biến động trong nhóm con do các nguyên nhân thông thường còn tất cả các nguyên nhân đặc biệt của biến động xảy ra giữa các nhóm con. Khi đó, vai trò chính của biểu đồ cusum là phân biệt giữa biến động do nguyên nhân thông thường và nguyên nhân đặc biệt. Do đó, việc chọn nhóm con có tầm quan trọng rất lớn. Ví dụ, lập ra mỗi nhóm con gồm bốn cá thể liên tiếp từ quá trình sản xuất tốc độ cao mỗi giờ, trái ngược với nhóm con được lấy cứ mười lăm phút một lần để tạo thành nhóm con gồm bốn nhóm mỗi giờ, sẽ đưa ra các biến động rất khác nhau làm cơ sở quyết định. Sai số chuẩn trong trường hợp đầu tiên sẽ rất nhỏ so với trường hợp thứ hai. Một biểu đồ cusum sẽ được lập với phần biến động liên tiếp là cơ sở ra quyết định trái với biến động giữa hai khoảng 15 phút đối với biểu đồ kia. Thước đo thích hợp của biến động cơ bản sẽ phụ thuộc vào thay đổi nào cần được báo hiệu.
Tuy nhiên, điều kiện tiên quyết là tính ổn định trong khoảng thời gian đủ để thiết lập thước đo định lượng tin cậy, như độ lệch chuẩn hoặc sai số chuẩn, quá hạn chế đối với một số lĩnh vực có thể áp dụng phương pháp cusum.
Ví dụ, các quan trắc của quá trình liên tục có thể đưa ra độ biến động không quan trọng nhỏ ở mức trung bình. Những thay đổi hệ thống hoặc lâu dài cần được đánh giá dựa trên các biến động này. ví dụ minh họa là:
a) quá trình công nghiệp được kiểm soát bằng bộ điều nhiệt hoặc thiết bị kiểm soát tự động khác;
b) chất lượng của nguyên liệu thô đầu vào có thể có độ biến động nhỏ không vi phạm quy định; và
c) trong việc theo dõi phản ứng của bệnh nhân để điều trị, có thể có những thay đổi nhỏ về chuyển hóa kèm theo bữa ăn, bệnh viện hoặc thói quen gia đình, v.v…, nhưng bất kỳ hiệu quả điều trị nào cũng cần được đánh giá dựa trên độ biến động điển hình tổng thể.
Mặt khác, mẫu có thể bao gồm đầu ra hoặc các quan trắc từ các nguồn khác nhau (khu vực hành chính, nhà máy, máy móc, người vận hành). Như vậy, có thể có quá nhiều biến động cục bộ cung cấp cơ sở thực tế cho việc đánh giá việc trung bình tổng thể có thay đổi hay không. Vì yếu tố này, cần xử lý cẩn thận dữ liệu phát sinh từ sự kết hợp các nguồn, như có thể bỏ qua mọi đặc thù cục bộ trong mỗi nguồn đóng góp. Hơn nữa, biến động giữa các nguồn có thể che khuất bất kỳ sự thay đổi nào xảy ra trên toàn hệ thống theo thời gian.
Một trong những giả định quan trọng trong quy trình cusum là độ lệch chuẩn quá trình s ổn định. Vì vậy, trước khi xây dựng quy trình cusum, cần đánh giá mọi quá trình để xem nó ở trạng thái kiểm soát thống kê (bằng cách sử dụng biểu đồ R, biểu đồ s hoặc biểu đồ độ rộng trượt) để có thể thu được ước lượng s đáng tin cậy.
Tương quan chuỗi giữa các quan trắc cũng có thể tự thể hiện – cụ thể, một quan trắc có thể có ảnh hưởng đến quan trắc tiếp theo. Minh họa cho tương quan chuỗi âm là sử dụng các số đọc đánh giá liên tiếp để ước lượng việc sử dụng nguyên liệu dạng đống, khi ước lượng quá cao trên một cơ hội sẽ có xu hướng đưa ra ước lượng thấp về số đọc tiếp theo. Một ví dụ khác là đặt hàng quá nhiều trong một tháng được bù trừ bằng đặt hàng ít hơn trong tháng tiếp theo. Tương quan chuỗi dương có thể xảy ra trong một số quá trình công nghiệp khi một lô nguyên liệu có thể kết hợp một phần với các lô trước đó và lô tiếp theo.
Ngân sách và kết thúc khoảng thanh toán, các giai đoạn quan trọng của dự án và thời hạn hợp đồng có thể ảnh hưởng đến việc phân bổ con số kinh doanh kế tiếp như chi phí và doanh thu theo từng giai đoạn, v.v…
Trên quan điểm về những khía cạnh này, cần xem xét các thước đo định lượng biến động khác trong chuỗi hay trình tự dữ liệu và trường hợp phù hợp.
Thước đo độ biến động làm cơ sở ra quyết định sử dụng cusum như vậy được xây dựng, theo hướng định lượng, trong Phụ lục A. Các khuyến nghị cũng được đưa ra để lựa chọn tùy theo hoàn cảnh.
7.3. Đo lường tính hiệu quả của quy tắc quyết định
7.3.1. Khái niệm cơ bản
Hiệu năng lý tưởng của quy tắc quyết định là đối với những thay đổi thực ít nhất có độ lớn xác định trước cần được phát hiện ngay và đối với quá trình không cho phép có thay đổi thực được phép duy trì mà không gây ra báo động sai. Trong thực tế điều này không thể đạt được. Thước đo đơn giản và thuận tiện hiệu quả thực tế của quy tắc quyết định là độ dài trung bình của loạt mẫu (ARL).
ARL là giá trị kỳ vọng của số mẫu được lấy dẫn đến quyết định là hiện có thay đổi thực.
Nếu không có sự thay đổi thực nào, thì giá trị lý tưởng của ARL là vô cùng. Mục tiêu thực tế trong tình huống đó là đưa ra ARL lớn. Ngược lại, khi có sự thay đổi thực, giá trị lý tưởng của ARL là 1, trong trường hợp này thay đổi được phát hiện khi lấy mẫu tiếp theo. Lựa chọn ARL là sự thỏa hiệp giữa hai yêu cầu trái ngược này. Đưa ra quyết định hành động không đúng khi quá trình không thay đổi sẽ gây ra “kiểm soát quá mức”. Trên thực tế, điều này sẽ làm tăng độ biến động. Không đưa ra hành động thích hợp khi quá trình có thay đổi sẽ dẫn đến “kiểm soát quá lỏng”. Trên thực tế, điều này cũng làm tăng độ biến động và cũng dẫn đến gia tăng chi phí sản xuất.
Tất nhiên ARL tùy thuộc vào độ biến động thống kê. Đôi khi có thể may mắn trong một loạt dài không nhận được báo động sai hoặc phát hiện sự thay đổi rất nhanh chóng. Đôi khi, loạt mẫu không may có thể tạo ra các báo động sai hoặc che khuất sự thay đổi thực do đó không tạo ra báo hiệu. Đôi khi dạng thực tế của biến động như vậy cần được chú ý. Tuy nhiên, nhìn chung, ARL được coi là thước đo hiệu quả hợp lý của quy tắc quyết định. Tóm lại, mục đích là:
|
Điều kiện quá trình thực |
Đáp ứng cusum cần thiết |
Đáp ứng lý tưởng |
|
Tại hoặc gần đích |
ARL dài (ít báo động sai) |
ARL = vô cùng |
|
Sai lệch đáng kể so với đích |
ARL ngắn (phát hiện nhanh) |
ARL = 1 |
7.3.2. Ví dụ về tính toán ARL
Khái niệm ARL không chỉ riêng với cusum. Lấy biểu đồ kiểm soát Shewhart chuẩn với các giới hạn kiểm soát đặt ở ±3 độ lệch chuẩn tính từ đường tâm. Trường hợp này được minh họa trong Hình 4 đối với phân bố chuẩn.
Phân bố thể hiện được gọi là “chuẩn hóa” trong đó có trung bình bằng “không” và độ lệch chuẩn bằng một.
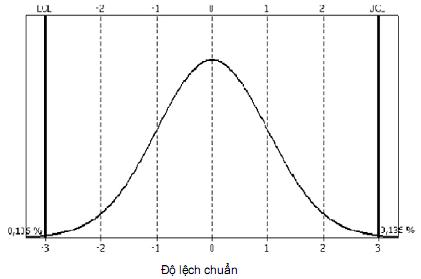
Hình 4 – Đồ thị phân bố chuẩn chuẩn hóa
Nhìn từ Hình 4 có một số 0,135 % các quan trắc, trung bình, nằm ngoài mỗi phía của các giới hạn này khi trung bình quá trình nằm trên đường tâm hoặc giá trị đích. Điều này có thể dễ dàng chuyển thành độ dài trung bình của loạt mẫu, ARL, bằng cách tính 1/0,001 35 = 741. Nói cách khác, ta sẽ có thể thấy giá trị trung bình vượt quá giới hạn kiểm soát trên chỉ một lần trong mỗi 741 khoảng quan trắc. Giá trị này sẽ tạo ra báo hiệu sai thay đổi về mức trong khi trên thực tế, thay đổi không xảy ra.
Vì thế trong thực tế, cần thiết kế hệ thống kiểm soát đảm bảo ARL cao khi quá trình vận hành ở giá trị đích.
Khi xem xét giới hạn hai phía, với trung bình quá trình vẫn tại đích, ARL giảm đi một nửa, lúc này nó là 1/(0,001 35 + 0,001 35) = 370.
Giả sử trung bình quá trình thay đổi một độ lệch chuẩn về phía giới hạn kiểm soát trên. Lúc đó, kỳ vọng là một số 2,28 % sẽ nằm trên giới hạn kiểm soát trên. ARL đối với UCL trở thành 1/0,022 8 = 44 với giới hạn một phía. Nói cách khác, trung bình, cần thêm 44 khoảng quan trắc để báo hiệu sự dịch chuyển về trung bình bằng một độ lệch chuẩn.
Khi xem xét giới hạn hai phía ở đây chỉ 0,003 2 % được dự kiến thấp hơn LCL vì trung bình quá trình bằng bốn độ lệch chuẩn tính từ LCL. Vì 1/(0,000 032 + 0,022 8) không ảnh hưởng nhiều đến ARL tính được cho một giới hạn nên với sự dịch chuyển về trung bình một độ lệch chuẩn, ARL đối với giới hạn hai phía xấp xỉ bằng với giới hạn một phía, cụ thể là 44.
Tóm lại:
|
Với trung bình ở giá trị đích |
ARL đối với giới hạn hai phía bằng một nửa của giới hạn một phía |
|
Khi sự dịch chuyển về mức trung bình tăng |
ARL đối với giới hạn hai phía gần như bằng với giới hạn một phía |
Tất nhiên, trong thực tế, các quy tắc báo hiệu khác như bổ sung giới hạn cảnh báo, loạt trên và dưới trung bình, v.v…, sẽ đảm bảo phát hiện nhanh sự dịch chuyển nhưng tăng chi phí báo hiệu sai khi quá trình tại đích. Biểu đồ Shewhart rất hấp dẫn và phổ biến vì cực kỳ đơn giản và hiệu quả trong việc phát hiện các nguyên nhân đặc biệt riêng rẽ làm phát sinh sự dịch chuyển lớn.
Tuy nhiên, cần thừa nhận rằng có sự hạn chế vốn có trong việc báo hiệu khác ngoài sự dịch chuyển lớn ngay cả khi chúng vẫn tồn tại mà không ảnh hưởng nghiêm trọng đến phạm vi báo động sai. Điều này cho thấy vai trò của một phương pháp khác nhằm phát hiện sự dịch chuyển nhanh hơn trong khi vẫn duy trì các ARL lâu dài khi ở đích. Phương pháp cusum rất thích hợp cho việc này.
8. Các loại chương trình quyết định cusum
8.1. Các loại mặt nạ V
Quy tắc quyết định đơn giản nhất để sử dụng cùng với biểu đồ cusum nằm trong mặt nạ loại V. Có bốn dạng mặt nạ hơi khác nhau, nhưng giống hệt nhau về nguyên tắc và tác dụng. Mục đích của chúng được giải thích trong các điều tiếp theo. Các loại là:
a) mặt nạ V cắt tỉa;
b) mặt nạ nửa parabôn; c) mặt nạ mũi hếch, và d) mặt nạ V hoàn chỉnh.
8.2. Mặt nạ V cắt tỉa
8.2.1. Hình dạng và kích thước
Mặt nạ V cắt tỉa “mục đích chung” được minh họa trong Hình 5. Nó bao gồm điểm mốc được biểu thị là O trên hình vẽ. Hai đường thẳng đứng xuất phát từ mốc, OB và OC, mỗi đoạn dài 5se đơn vị (nghĩa là H = 5se). Hai đường này được gọi là khoảng quyết định. Hai cạnh nghiêng, BA và CD, được gọi là đường quyết định, có thể kéo dài theo yêu cầu để bao gồm các điểm cusum được vẽ. Về kích thước, EO bằng 10 khoảng quan trắc và khoảng cách EA và ED theo chiều thẳng đứng đều bằng 10se đơn vị (nghĩa là cho độ dốc F = 0,5se).
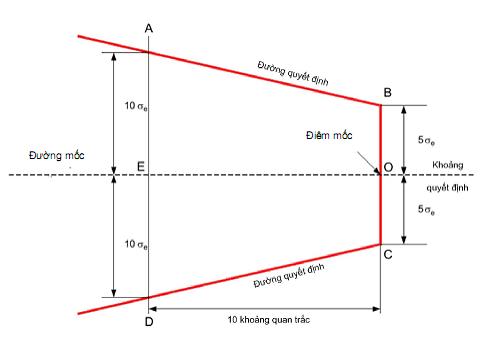
Hình 5 – Hình dạng và kích thước mặt nạ V cắt tỉa mục đích chung
Mặt nạ V cắt tỉa vẽ theo tỷ lệ thực tế được thể hiện trong Hình 6 đối với biến quá trình có độ lệch chuẩn là 0,2. Ở đây sử dụng độ lệch chuẩn, chứ không phải là sai số chuẩn, vì mặt nạ cụ thể được tạo ra để theo dõi các quan trắc riêng lẻ chứ không phải là giá trị trung bình.
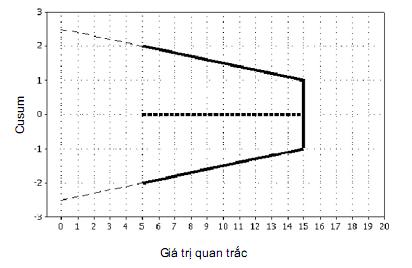
Hình 6 – Mặt nạ V được vẽ theo tỷ lệ thực tế cho đặc trưng quá trình với độ biến động vốn có cụ thể (độ lệch chuẩn = 0,2)
8.2.2. Ứng dụng của mặt nạ V cắt tỉa
Mặt nạ được sử dụng bằng cách đặt điểm mốc tại giá trị vẽ đồ thị được lựa chọn trên biểu đồ cusum, với đường mốc nằm ngang trên biểu đồ. Trong tình huống kiểm soát liên tục, giá trị vẽ đồ thị được lựa chọn thường là điểm mới nhất.
Nếu đường cusum nằm trong cạnh dốc của mặt nạ (hay phần kéo dài của chúng vượt ra ngoài A và D) thì không có sự dịch chuyển đáng kể nào ở mức trung bình được chỉ ra cho đến giá trị được vẽ đó. Trong tình huống kiểm soát, quá trình khi đó được coi là trong trạng thái kiểm soát thống kê so với giá trị đích. Tuy nhiên, nếu đường cusum thay đổi vị trí bên ngoài cạnh dốc của mặt nạ, thì sự lệch hướng đáng kể từ giá trị đích được báo hiệu. Trong quản lý quá trình, lúc này quá trình được gọi là mất kiểm soát.
Hình 7 minh họa tình huống “được kiểm soát” khi không có sự lệch hướng đáng kể nào so với giá trị đích được phát hiện, và hai tình huống “mất kiểm soát”, một là khi có sự giảm đáng kể về giá trị được thể hiện và trường hợp thứ hai là khi có sự gia tăng đáng kể. Độ lệch chuẩn 0,2 được sử dụng trong ba hình minh họa của Hình 7. Giá trị đích được sử dụng để xây dựng biểu đồ cusum bằng với trung bình đích đối với quá trình.
Tình trạng hiện tại được xác định bằng cách lập mặt nạ V cho biểu đồ cusum từng bước theo các điểm dữ liệu tích lũy.
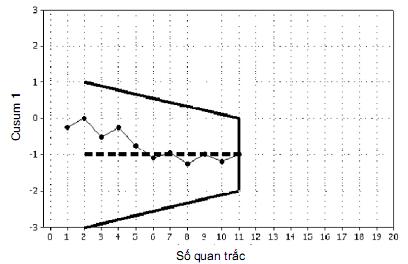
a) Không có thay đổi đáng kể về trung bình quá trình so với giá trị đích cusum
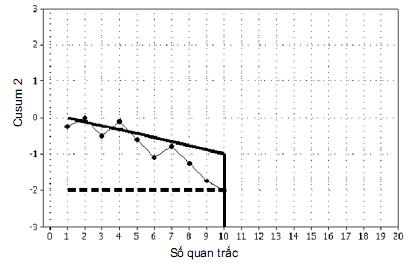
b) Trung bình quá trình giảm đáng kể so với giá trị đích
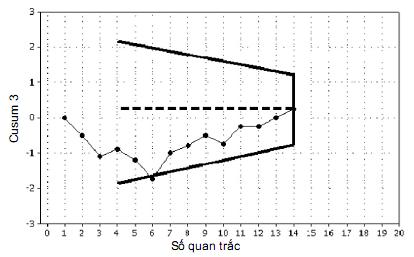
c) Trung bình quá trình tăng đáng kể so với giá trị đích
Hình 7 – Hình minh họa việc sử dụng mặt nạ V cắt tỉa để phát hiện sự thay đổi đáng kể về trung bình quá trình
Mặc dù Hình 7 a) cho biết trung bình quá trình nhỏ hơn giá trị đích cusum nhưng mặt nạ V chưa thể hiện sự thay đổi này như là sai lệch đáng kể.
Hình 7 b) cho thấy trung bình quá trình thấp hơn đáng kể so với giá trị đích. Trong khi sai lệch đáng kể không được phát hiện cho đến quan trắc 10, từ góc độ trực quan trung bình quá trình dường như vận hành ở mức thấp ngay từ quan trắc 1. Bằng cách ghi lại đường dốc của đường thẳng đi qua các điểm quan trắc, có thể thực hiện việc đánh giá trung bình thực tế của quá trình. Điều này sẽ đưa ra hướng dẫn về mức độ điều chỉnh cần thiết để đưa quá trình về giá trị đích của nó, và chỉ số chẩn đoán để xác định những gì xảy ra tại quan trắc 1 để trước hết đặt quá trình ở mức thấp này.
Hình 7 c) cho thấy trung bình quá trình lớn hơn đáng kể so với giá trị đích. Điều này không được ghi nhận là đáng kể cho đến quan trắc 14. Có thể thấy rằng quá trình này dường như vận hành thấp hơn giá trị đích cho đến quan trắc 6 nhưng không đủ để gây ra điều kiện mất kiểm soát. Sau đó, theo quan trắc 6, mức đã thay đổi sang giá trị cao hơn giá trị đích. Bằng cách đo dốc đường thẳng lên đến và từ quan trắc 6, cùng với quan trắc ban đầu của nó, công cụ điều chỉnh và trợ giúp chẩn đoán đều được đưa ra.
Khi chỉ áp dụng giới hạn quy định trên hoặc dưới, kiểm soát một phía là thích hợp. Khi đó, có thể sử dụng một nửa mặt nạ. Khi theo dõi dựa trên sự dịch chuyển lên/xuống, chỉ phần dưới/trên tương ứng của mặt nạ là cần thiết. Tuy nhiên, mặt nạ hoàn chỉnh có thể vẫn được ưu tiên hơn trên cơ sở đơn giản và thông tin. Có thể bỏ qua bất kỳ sự dịch chuyển nào theo hướng không thích hợp từ quan điểm quy định, hoặc được sử dụng để hướng sự chú ý đến sự dịch chuyển đáng kể theo hướng mong đợi hơn.
8.2.3. Độ dài trung bình của loạt mẫu
Thuộc tính độ dài trung bình của loạt mẫu (ARL) đối với mặt nạ V cắt tỉa mục đích chung với kích thước cho trên Hình 8 được liệt kê trong Bảng 4 đối với độ lệch chuẩn, hay sai số chuẩn, của biến được vẽ. ARL cusum được so sánh với các biến có hai quy tắc quyết định liên quan đến các phương pháp kiểm soát chuẩn quốc tế được thiết lập tốt.
Các quy tắc này là:
– Quy tắc Shewhart 1: một điểm nằm ngoài các giới hạn hành động hoặc giới hạn kiểm soát, cụ thể là ± 3 độ lệch chuẩn tính từ đường tâm;
– Quy tắc Shewhart 2: hai điểm liên tiếp nằm ngoài các giới hạn cảnh báo, cụ thể là ± 2 độ lệch chuẩn tính từ đường tâm.
CHÚ THÍCH: Giả định biến được vẽ đồ thị có phân bố chuẩn với độ lệch chuẩn s.
CHÚ THÍCH 2: Độ dài trung bình của loạt mẫu đề cập đến kiểm soát một phía của trung bình. Khi chọn kiểm soát hai phía từ một giá trị đích, ARL ở giá trị đích giảm một nửa (có gấp hai lần số báo động sai), nhưng đối với sự dịch chuyển lớn về trung bình, ARL không bị ảnh hưởng.
CHÚ THÍCH 3: Cusum chuẩn đề cập có h (chiều cao của khoảng quyết định) = 5,0 và ¦ (độ dốc của đường quyết định) = 0,5 như trên Hình 4. Giới hạn Hành động Shewhart chỉ liên quan đến Quy tắc Shewhart 1. Giới hạn Hành động Shewhart và Giới hạn cảnh báo áp dụng cho sự kết hợp quy tắc Shewhart 1 và 2.
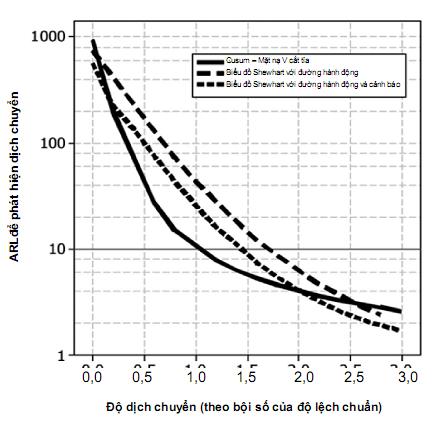
Hình 8 – Độ dài trung bình của loạt mẫu, liên quan đến sự dịch chuyển từ giá trị đích, đối với mặt nạ V cắt tỉa mục đích chung so sánh với biểu đồ kiểm soát Shewhart chuẩn
Bảng 4 – Độ dài trung bình của loạt mẫu liên quan đến sự dịch chuyển từ giá trị đích đối với mặt nạ V cắt tỉa mục đích chung của Hình 5 so sánh với biểu đồ kiểm soát Shewhart chuẩn bằng cách sử dụng bộ hai quy tắc
|
Sự dịch chuyển trung bình quá trình từ giá trị đích (theo đơn vị se) |
Độ dài trung bình của loạt mẫu |
||
|
Mặt nạ V cắt tỉa chuẩn |
Biểu đồ kiểm soát Shewhart với giới hạn hành động |
Biểu đồ kiểm soát Shewhart với giới hạn hành động và giới hạn cảnh báo |
|
|
0,0 |
931,0 |
741,0 |
556,0 |
|
0,2 |
198,0 |
308,0 |
223,0 |
|
0,4 |
60,0 |
200,0 |
134,0 |
|
0,6 |
27,0 |
120,0 |
75,0 |
|
0,8 |
15,0 |
72,0 |
43,0 |
|
1,0 |
10,0 |
44,0 |
26,0 |
|
1,2 |
7,8 |
28,0 |
16,0 |
|
1,4 |
6,3 |
18,0 |
11,0 |
|
1,6 |
5,3 |
12,0 |
7,4 |
|
1,8 |
4,6 |
8,7 |
5,4 |
|
2,0 |
4,0 |
6,3 |
4,1 |
|
2,2 |
3,6 |
4,7 |
3,2 |
|
2,4 |
3,3 |
3,7 |
2,6 |
|
2,6 |
3,0 |
2,9 |
2,2 |
|
2,.8 |
2,8 |
2,4 |
1,9 |
|
3,0 |
2,6 |
2,0 |
1,7 |
ARL là chỉ số tính hiệu quả của phương pháp quyết định:
– ARL tại giá trị đích càng cao thì xác suất báo động sai càng thấp;
– ARL ở độ lệch trung bình từ giá trị đích của chúng càng thấp thì việc phát hiện thay đổi càng nhanh.
Hình 8 và Bảng 4 cho thấy như sau:
a) Giá trị L0 (ARL tại dịch chuyển bằng “không”) của biểu đồ cusum lớn hơn so với biểu đồ Shewhart với các giới hạn hành động, trong khi biểu đồ Shewhart với giới hạn hành động và giới hạn cảnh báo có giá trị L0 nhỏ hơn. Như vậy trong số ba biểu đồ, biểu đồ cusum có tỷ lệ báo động sai thấp nhất, trong khi biểu đồ Shewhart với giới hạn hành động và giới hạn cảnh báo có tỷ lệ báo động sai cao nhất.
b) Đối với dịch chuyển lên tới 2se, ARL của biểu đồ cusum thấp hơn ARL của các biểu đồ khác chỉ ra đáp ứng trung bình nhanh hơn đối với dịch chuyển. Điều này đặc biệt đúng trong vùng 4se đến 1,4se.
c) Đối với dịch chuyển lớn hơn 2se, biểu đồ Shewhart với quy tắc hành động và quy tắc cảnh báo đáp ứng nhanh hơn biểu đồ cusum. Đối với dịch chuyển lớn hơn 2,4se, biểu đồ Shewhart với giới hạn hành động và giới hạn cảnh báo đáp ứng nhanh hơn biểu đồ cusum. Tuy nhiên, đáp ứng nhanh hơn này của biểu đồ Shewhart là ở chi phí tỷ lệ báo động sai hơn.
8.2.4. Bình luận chung về độ dài trung bình của loạt mẫu
Trước tiên, kích thước của mặt nạ V cắt tỉa mục đích chung, hoặc chuẩn, được thiết kế đặc biệt thích hợp cho việc phát hiện dịch chuyển trong miền của một sai số chuẩn (1se). Nếu trọng tâm là dịch chuyển khác thì sử dụng giá trị h và ¦ khác. Ngoài ra, có thể sử dụng mặt nạ V với các cấu hình hoặc hình dạng khác với loại mặt nạ cắt tỉa để cải thiện thuộc tính của ARL và do đó thay đổi hiệu năng phát hiện. Ví dụ như mặt nạ V nửa parabôn và mặt nạ V mũi hếch được thảo luận tương ứng trong 8.4 và 8.5.
Thứ hai, quy tắc vận hành bổ sung thường được sử dụng kết hợp với biểu đồ kiểm soát Shewhart. Các quy tắc này bao gồm “7 điểm liên tiếp trên một phía của trung bình” và “7 khoảng được vẽ liên tiếp đều tăng hoặc đều giảm”. Vấn đề của những quy tắc này là chúng làm giảm đáng kể giá trị của ARL khi trung bình quá trình tại đích, do đó tăng đáng kể rủi ro báo động sai.
Thứ ba, có một số yếu tố ảnh hưởng đến độ ổn định của thước đo ARL. Các yếu tố này bao gồm mô hình dạng biến động cơ bản, giá trị của se và tính độc lập của giá trị quan trắc. Bảng ARL được cho trong Bảng 4 và Hình 8 dựa trên ba giả định:
a) quan trắc được phân bố chuẩn;
b) độ lệch chuẩn được biết chính xác; và
c) các quan trắc liên tiếp độc lập về thống kê.
Phân bố chuẩn là đối xứng. Nhìn chung, độ bất đối xứng có đuôi dài hơn đồng nghĩa với hướng dịch chuyển tiềm ẩn, trong kiểm soát một phía, sẽ rút ngắn ARL đích, nhưng có ít ảnh hưởng về ARL đối với dịch chuyển lớn hơn về trung bình. Ngược lại, nếu đuôi ngắn hơn theo hướng dịch chuyển tiềm ẩn thì ARL ở mức đích sẽ được kéo dài đáng kể và cũng ít ảnh hưởng đến ARL đối với dịch chuyển lớn.
Độ lệch chuẩn, hoặc sai số chuẩn, thường được ước lượng từ cùng tập hợp các quan trắc được sử dụng để vẽ đồ thị cusum. Sai số 10 % hoặc nhiều hơn là không phổ biến. Ước lượng quá cao se làm tăng ARL, và ước lượng thấp làm giảm ARL. Sự biến dạng này của ARL rõ ràng nhất tại hoặc gần các điều kiện đích nhưng có ít ảnh hưởng ở dịch chuyển lớn. Bảng 5 chỉ thị sự biến dạng trong các ARL đối với sai số 10 % trong ước lượng se.
Bảng 5 – Minh họa về ảnh hưởng đến ARL của giá trị sai số chuẩn, se, không đúng
|
Dịch chuyển trung bình quá trình khỏi giá trị đích, đơn vị se thực |
Độ dài trung bình của loạt mẫu (ARL) |
||
|
Ước lượng quá 10 % se |
Ước lượng đúng se |
Ước lượng dưới 10 % se |
|
|
0,0 |
3 000,0 |
930,0 |
410,0 |
|
0,5 |
45,0 |
38,0 |
35,0 |
|
1,0 |
10,0 |
10,5 |
10,0 |
|
1,5 |
6,0 |
5,8 |
6,0 |
|
2,0 |
4,4 |
4,1 |
4,5 |
Sự tự tương quan dương có xu hướng rút ngắn ARL và tự tương quan âm kéo dài ARL.
Cần lưu ý rằng các tác động của ba giả định này được thảo luận ở đây không chỉ là đặc thù đối với biểu đồ cusum mà còn áp dụng được cho các phương pháp phân tích biểu đồ khác.
8.3. Cách tiếp cận thiết kế thay thế
Cách tiếp cận thiết kế thay thế, nhằm cải thiện đặc trưng hiệu năng trong phạm vi độ rộng của dịch chuyển trung bình lớn hơn, là sử dụng mặt nạ V nửa parabôn (xem 8.4), mặt nạ V mũi hếch (xem 8.5), hoặc cusum đáp ứng ban đầu nhanh (FIR) (xem 8.7).
So sánh hiệu năng của những thiết kế thay thế này cùng với mặt nạ V cắt tỉa chuẩn hóa được thể hiện trong Bảng 6.
Bảng 6 – Độ dài trung bình của loạt mẫu (ARL) đối với các mặt nạ cusum khác nhau
Dịch chuyển trung bình so với đích (đơn vị se)
|
Dịch chuyển trung bình so với đích (đơn vị se) |
Mặt nạ V cắt tỉa (h = 5; ¦ = 0,5) |
Mặt nạ V nửa parabôn (như quy định trong Bảng 7) |
Mặt nạ V mũi hếch (h = 5; ¦ = 0,5 và h = 2,05; ¦ = 1,3) |
Mặt nạ V cắt tỉa FIR (h = 5; ¦ = 0,5) |
|
0,00 |
465,0 |
235,0 |
300,0 |
448,0 |
|
0,25 |
142,0 |
113,0 |
114,0 |
125,0 |
|
0,50 |
38,0 |
36,0 |
36,0 |
29,0 |
|
1,00 |
10,0 |
10,0 |
10,0 |
6,4 |
|
1,50 |
5,8 |
5,3 |
5,3 |
3,4 |
|
2,00 |
4,0 |
3,3 |
3,3 |
2,4 |
|
2,50 |
3,1 |
2,3 |
2,3 |
1,9 |
|
3,00 |
2,6 |
1,7 |
1,8 |
1,5 |
|
3,50 |
2,2 |
1,4 |
1,5 |
1,3 |
|
4,00 |
2,0 |
1,2 |
1,3 |
1,2 |
8.4. Mặt nạ V nửa parabôn
Mặt nạ V cắt tỉa mục đích chung, hoặc chuẩn hóa, được chọn với các tham số h = 5 và ¦ = 0,5. Có thể lựa chọn các giá trị tham số h và ¦ khác nhau của mặt nạ V cắt tỉa để cho đáp ứng nhanh đối với sự dịch chuyển về trung bình có cỡ cụ thể. Trong các trường hợp khác, một số ngành công nghiệp như công nghiệp thực phẩm, nếu cần phải cải tiến tốc độ phát hiện sự dịch chuyển trung bình lớn hơn trong khi vẫn giữ tính ưu việt của cusum trong việc báo hiệu sự dịch chuyển nhỏ hơn thì cần thay đổi kiểu mặt nạ.
Một giải pháp khác là mặt nạ nửa parabôn trong đó biên dạng cong được thể hiện thành mặt nạ cắt tỉa gần đầu thu hẹp của nó như thể hiện trên Hình 9.
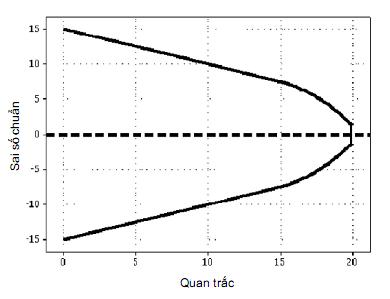
Hình 9 – Hình minh họa mặt nạ nửa parabôn
Cơ sở của mặt nạ nửa parabôn ở Hình 9 là mặt nạ V cắt tỉa mục đích chung ở Hình 5. Tuy nhiên, trên năm khoảng quan trắc cuối cùng ở đầu thu hẹp, mặt nạ uốn cong có độ rộng 1,25se chứ không phải là 5se. Dữ liệu để xây dựng mặt nạ được cho trong Bảng 7.
Bảng 7 – Dữ liệu đối với việc xây dựng mặt nạ nửa parabôn
|
Khoảng cách từ mốc, J (khoảng quan trắc, J) |
0 |
1 |
2 |
3 |
4 |
5 |
10 |
20 |
|
Nửa độ rộng của mặt nạ tại J (đơn vị của se) |
1,25 |
3,10 |
4,65 |
5,90 |
6,85 |
7,50 |
10,00 |
15,00 |
|
Chi tiết xây dựng |
Ynửa độ rộng của mặt nạ tại J = 1,25 + 2,00J – 0,15 J2 |
Tuyến tính |
||||||
Hiệu năng hoạt động của mặt nạ nửa parabôn là:
a) tốt hơn so với mặt nạ V cắt tỉa bắt đầu từ không chuẩn hóa trên toàn độ rộng của sự dịch chuyển trung bình. Tuy nhiên, điều này đạt được với chi phí gần như gấp đôi về tỷ lệ báo động sai ở giá trị đích;
b) kém hơn so với mặt nạ V cắt tỉa FIR chuẩn hóa cả về tỷ lệ báo động sai và báo hiệu sự dịch chuyển về trung bình ngoài dịch chuyển nhỏ hơn 0,5 độ lệch chuẩn; và
c) kém hơn so với mặt nạ mũi hếch thể hiện ở báo động sai tại giá trị đích trong khi có hiệu năng tương đương trong việc phát hiện sự dịch chuyển về trung bình.
Những tính năng này được thể hiện trong Bảng 6 cho thấy ARL tương đương, liên quan đến sự dịch chuyển về trung bình, đối với các quy tắc quyết định cusum khác.
8.5. Mặt nạ V mũi hếch
Mặt nạ V mũi hếch nhằm đạt được những lợi ích tương tự như mặt nạ V nửa parabôn nhưng với quy trình thiết lập đơn giản hơn. Vì vậy nó rất hữu ích trong ứng dụng khi đáp ứng sớm hơn đối với dịch chuyển lớn là cần thiết. Điều này đạt được bằng cách xếp chồng hai hoặc nhiều mặt nạ V cắt tỉa. Minh họa được thể hiện trên Hình 10 đối với mặt nạ V cắt tỉa với h = 2,05 và ¦ = 1,5, chồng lên trên mặt nạ chuẩn hóa với h = 5,0 và ¦ = 0,5. Bảng 6 minh họa mặt nạ mũi hếch này mang lại hiệu năng tốt gần như mặt nạ V cắt tỉa nửa parabôn trong phạm vi độ rộng của dịch chuyển rộng hơn thu được nhờ mặt nạ V cắt tỉa chuẩn hóa.
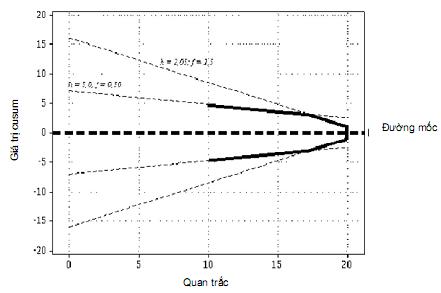
Hình 10 – Hình minh họa mặt nạ V mũi hếch
8.6. Mặt nạ V hoàn chỉnh
Các quy tắc quyết định cũng có thể được áp dụng bằng cách sử dụng mặt nạ V hoàn chỉnh, như được thể hiện trên Hình 11. Mặt nạ này có đặc trưng hiệu năng giống với mặt nạ cắt tỉa vì vậy thảo luận được rút ngắn.
Hình 11 cho thấy các đường quyết định cắt nhau tại đỉnh O. Điều này có nghĩa là không còn điểm mốc nữa và đỉnh nằm trên biểu đồ cusum tạo ra khoảng cách OA kéo dài về phía trước (bên phải) ứng với quan trắc mới nhất trong dãy quan trắc của đặc trưng quan tâm. OA được gọi là khoảng cách tính từ đỉnh mặt nạ, d. Đối với các đặc trưng giống với mặt nạ V cắt tỉa chuẩn đã nêu, H = 5se và d = 10 đơn vị quan trắc.
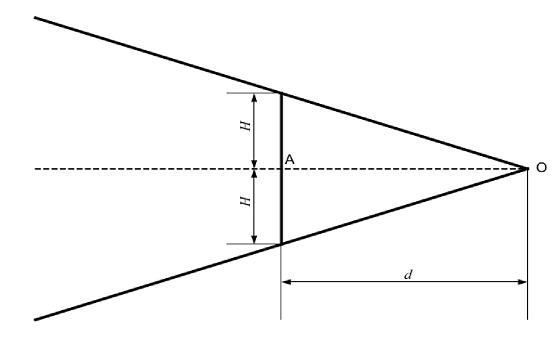
Hình 11 – Mặt nạ V hoàn chỉnh
8.7. Cusum đáp ứng ban đầu nhanh (FIR)
Cusum đáp ứng ban đầu nhanh (FIR) nhằm giảm ARL đối với dịch chuyển về của trung bình đó là mong muốn phát hiện mà không làm giảm đáng kể ARL tại đích: điều này liên quan đến chuẩn mực quyết định so sánh thông thường. Nói cách khác, mục tiêu là để đáp ứng nhanh hơn với sự dịch chuyển trong khi vẫn duy trì tỷ lệ báo động sai.
So sánh các ARL trong cột 2 và 5 của Bảng 6 cho thấy chương trình FIR có đáp ứng nhanh hơn nhiều đối với dịch chuyển về của trung bình trong toàn độ rộng (29 thay cho 38 tại 0,5se và 6,4 thay cho 10 tại 1se) trong khi vẫn duy trì khả năng so sánh về ARL đích, 448 được so sánh với 465.
Bảng 6 cũng cho thấy chương trình FIR có đáp ứng nhanh hơn đối với sự dịch chuyển so với mặt nạ nửa parabôn hoặc mặt nạ mũi hếch trong toàn độ rộng và đồng thời, có ARL tại đích ưu việt hơn nhiều (448 được so sánh với 235 và 300).
Với FIR, thay vì tích lũy từ “không”, có một điểm khởi đầu đối với cusum. Giá trị thuận tiện cho khởi đầu này nhìn chung được chấp nhận là một nửa khoảng quyết định, h/2.
Lý do đằng sau cusum FIR là nếu có một dịch chuyển trước, hoặc khi, biểu đồ cusum bắt đầu thì bắt đầu phần cusum theo hướng nó chuyển động sẽ đẩy nhanh báo hiệu dịch chuyển về trung bình. Mặt khác, nếu quá trình không di chuyển, cusum sẽ lùi về phía “không” và vận hành giống như cusum khởi đầu từ “không” bình thường.
Khi được sử dụng kết hợp với chương trình quyết định dạng bảng (xem 8.8), điểm khởi đầu thường được sử dụng với cả cusum trên và dưới.
8.8. Cusum dạng bảng
8.8.1. Thuyết minh
Đôi khi mục đích chính của quy trình cusum đơn thuần là phát hiện các điều kiện ngoài chuẩn, hơn là thể hiện trực quan thông tin về dữ liệu liên tiếp. Như vậy, có thể ghi lại thông tin cusum theo dạng bảng thay cho biểu đồ. Quy tắc quyết định bằng số thay thế mặt nạ được sử dụng với biểu đồ cusum thông thường.
Chương trình như vậy được gọi là cusum bảng.
Mặt nạ V phát hiện những thay đổi trong đường dốc. Khoảng quyết định của nó, hse, cho phép có mức độ phân tán trong các điểm cusum. Đường dốc đường quyết định của mặt nạ tương ứng với mức quá trình trung bình của “giá trị đích ± ¦se”.
Với chương trình dạng bảng, thay vì tích lũy và vẽ đồ thị:
giá trị quan trắc – giá trị đích,
Ta tích lũy riêng và lập bảng:
giá trị quan trắc – (giá trị đích + ¦se),
đặt lại giá trị tổng tích lũy từ “không” trở thành âm, đối với cusum trên để phát hiện sự tăng của trung bình; và
tích lũy và lập bảng:
giá trị quan trắc – (giá trị đích – ¦se),
đặt lại giá trị tổng tích lũy về “không” trở thành dương, đối với cusum dưới để phát hiện sự giảm của trung bình.
Điều này đưa ra:
đường quyết định nằm ngang tại “± hse”,
thay vì:
đường quyết định với đường dốc “¦se” phân tán từ mốc “hse”, của mặt nạ V.
Về quyết định thống kê thuần túy, tác động giống hệt như thu được với mặt nạ V so sánh.
8.8.2. Phương pháp cusum dạng bảng
Các bước sau đây được thực hiện trong việc thiết lập và giải thích chương trình khoảng quyết định cusum hai phía đối với đặc trưng dữ liệu được đo có phân bố chuẩn.
Bước 1 – Thiết lập các tham số cusum
a) Thiết lập khoảng quyết định, h.
b) Thiết lập đường dốc đường quyết định, ¦.
c) Thiết lập giá trị đích, T.
d) Ước lượng sai số chuẩn của đặc trưng, se.
Bước 2 – Tính chuẩn mực cusum
Tính (T + ¦se) và (T – ¦se).
Bước 3 – Chuẩn bị bảng cusum theo cột, đối với cusum lập bảng trên để phát hiện sự tăng lên về mức trung bình
e) Số quan trắc.
f) Giá trị.
g) Giá trị – (T + ¦se).
h) Cusum của [Giá trị – (T + ¦se)].
CHÚ THÍCH: Đây là bảng tương tự như được sử dụng cho đồ thị cusum thông thường ngoại trừ (T + ¦se) thay thế giá trị T, ¦se, là đường dốc của đường quyết định mặt nạ V tương đương.
Bước 4 – Chuẩn bị bảng cusum theo cột, đối với cusum bảng dưới để phát hiện sự giảm về mức trung bình
Như với Bước 3, ngoại trừ:
i) Giá trị – (T – ¦se).
j) Cusum của [Giá trị – (T – ¦se)].
Bước 5 – Nhập dữ liệu
k) Nhập dữ liệu và thực hiện các phép tính.
l) Đối với giá trị cusum dương: Bắt đầu tại “không”, tích lũy cột “Cusum của [Giá trị – (T + ¦se)]”. Nếu cusum âm tại bất kỳ điểm nào, điều chỉnh lại về “không” và tiếp tục tại “không” đến khi cusum dương trở lại. Nếu cusum chạm tới hoặc vượt quá biên giới quyết định, hse, thì báo hiệu sự dịch chuyển hướng lên.
m) Đối với giá trị cusum âm: Bắt đầu tại “không”, tích lũy cột “Cusum của [Giá trị – (T – ¦se)]”. Nếu cusum dương tại bất kỳ điểm nào, điều chỉnh lại về “không” và tiếp tục tại “không” đến khi cusum trở thành âm. Nếu cusum chạm tới hoặc xuống thấp hơn biên giới quyết định, hse, thì báo hiệu sự dịch chuyển đi xuống.
Ví dụ về phương pháp được thể hiện trong Bảng 8 và một ví dụ khác về phương pháp bảng nêu trong Phụ lục B.
Bảng 8 – Ví dụ về chương trình cusum bảng
|
Giá trị |
Giá trị – 11 |
Cusum (trên) |
Giá trị – 9 |
Cusum (dưới) |
Bình luận |
|
10 |
-1 |
0 |
+1 |
0 |
Cả hai cusum bằng “không” vì quá trình tại đích |
|
10 |
-1 |
0 |
+1 |
0 |
|
|
10 |
-1 |
0 |
+1 |
0 |
|
|
14 |
+3 |
+3 |
+5 |
0 |
Trung bình quá trình cao hơn đích do đó cusum dưới bằng “không” |
|
14 |
+3 |
+6 |
+5 |
0 |
|
|
3 |
-8 |
0 |
-6 |
-6 |
|
|
3 |
-8 |
0 |
-6 |
-12a |
a Báo hiệu trung bình thấp |
|
10 |
-1 |
0 |
+1 |
-11 |
|
|
10 |
-1 |
0 |
+1 |
-10 |
|
|
10 |
-1 |
0 |
+1 |
-9 |
|
|
10 |
-1 |
0 |
+1 |
-8 |
|
|
10 |
-1 |
0 |
+1 |
-7 |
|
|
17 |
+6 |
+6 |
+8 |
0 |
|
|
17 |
+6 |
+12b |
+8 |
0 |
b Báo hiệu trung bình cao |
|
CHÚ THÍCH 1: Giá trị đích = T = 10: se = 2: h = 5, ¦ = 0,5. CHÚ THÍCH 2: Cột 2 = Giá trị – (T + ¦se) = Giá trị – (10 + 1) = Giá trị – 11. CHÚ THÍCH 3: Cột 4 = Giá trị – (T – ¦se) = Giá trị – (10 – 1) = Giá trị – 9. |
|||||
9. Phương pháp cusum đối với kiểm soát quá trình và chất lượng
9.1. Tính chất các thay đổi cần được phát hiện
9.1.1. Mức độ thay đổi cần phát hiện
Khi thiết kế hệ thống cusum để theo dõi tham số quá trình hoặc đặc trưng sản phẩm, cần xem xét về mức độ dịch chuyển hoặc thay đổi trong tham số hay đặc trưng quan trọng cần phát hiện. Quyết định này sẽ ảnh hưởng đến hình dạng của bất kỳ “mặt nạ V” nào có thể được sử dụng để quan sát báo hiệu mất kiểm soát. Khi kiểm soát tham số hoặc đặc trưng, nhiều chuyên gia lấy là sự dịch chuyển nhỏ nhất tại đó có thể điều chỉnh quá trình. Có điểm nhỏ trong việc tìm sự dịch chuyển nhỏ hơn đối với tác động trên đồ thị cusum có khả năng tạo ra hiện tượng “thăng giáng” (xem 9.1.5).
Những thay đổi xảy ra có thể được phân loại là “nấc”, “độ trôi” hoặc “chu kỳ ”.
9.1.2. Thay đổi “nấc”
Thay đổi nấc là thay đổi trong đó dữ liệu từ phép đo được thực hiện trên tham số quá trình hoặc đặc trưng sản phẩm đột nhiên nhảy hoặc “chuyển nấc” sang một mức độ mới. Ví dụ như khi sử dụng lô nguyên liệu thô mới khác với lô được sử dụng trước đó, hoặc nhân viên thiếu kinh nghiệm đảm nhận công việc quản lý và gây ra lỗi nhiều hơn người có kinh nghiệm, cho đến khi người đó học đúng cách các công việc cần thiết. Biểu đồ cusum sẽ nhận biết sự thay đổi này bằng cách thể hiện độ dốc đáng kể.
9.1.3. Độ trôi
Kiểu thay đổi này thường được kết hợp với các dạng hao mòn của thiết bị hoặc công cụ nhưng có thể xảy ra, trong trường hợp con người, khi tiêu chuẩn thay đổi theo thời gian, ví dụ: tiêu chuẩn kiểm tra. Dạng thức sẽ được phát hiện bằng đồ thị cusum và được mô tả bằng độ dốc tăng (hoặc giảm).
9.1.4. Chu kỳ
Dạng thay đổi theo thời gian và lặp lại chính dạng đó được gọi là thay đổi chu kỳ. Ví dụ, nó có thể xảy ra trong nhà máy có ba ca làm việc và cả ba công nhân thực hiện cùng một nhiệm vụ tương tự theo cách khác biệt. Vì có trình tự nhất định của các ca, ví dụ: Ca B luôn sau Ca A, dạng chu kỳ sẽ xuất hiện. Đồ thị cusum thể hiện dạng này như chu kỳ khi độ dốc đi theo hướng tiếp nối nhau cho đến khi nó thay đổi trở lại, v.v…
9.1.5. Sự thăng giáng
Sự thăng giáng xảy ra khi không thể điều chỉnh chính xác tham số hoặc đặc trưng theo giá trị đích mong muốn, và kéo theo báo hiệu mất kiểm soát, sự điều chỉnh đưa vị trí của tham số hoặc đặc trưng về phía kia của đích. Đồ thị cusum xây dựng độ dốc theo hướng ngược lại và cuối cùng nhận báo hiệu để thay đổi điều chỉnh đã được thực hiện trước đó.
Bằng cách này, dạng “zic zắc” sẽ được phát hiện trên đồ thị cusum. Rõ ràng đây là tình huống không thỏa mãn nhất và cần tránh bằng cách lựa chọn cẩn thận “giá trị đích” ban đầu và cần điều chỉnh ở mức tối thiểu tiếp theo. Xem 9.3.1 Bước 13 c) đối với sự thăng giáng trung hòa hơn.
9.2. Lựa chọn các giá trị đích
9.2.1. Khái quát
Lựa chọn đúng giá trị đích là điều quan trọng hàng đầu trong thiết lập chương trình cusum.
Giá trị đích nằm giữa hai giá trị có cùng khả năng chấp nhận sẽ tạo ra “sự thăng giáng” như được mô tả trong 9.1.5.
9.2.2. Giá trị chuẩn (cho trước) làm giá trị đích
Giá trị đích đơn giản nhất để gán là giá trị “cho trước” hoặc “gán trước”. Khi chọn cách này, giá trị đích thường được đặt bằng một giá trị quy định như giá trị danh nghĩa hoặc giá trị giữa dung sai. Những giá trị này được nêu trong các tài liệu quy định hoặc bản vẽ khi ứng dụng dựa trên kỹ thuật. Nếu ứng dụng cusum là phi sản xuất, đích đã cho có thể là một mức hiệu năng như thời gian dự kiến để xử lý hóa đơn hoặc chi tiêu hàng tháng được dự toán đối với phòng ban trong công ty.
Bản thân giá trị đích có thể thay đổi. Ví dụ, nếu theo dõi doanh thu bán kem bằng biểu đồ cusum trên cơ sở hàng tháng, giá trị đích được sử dụng có thể khác theo thời gian trong năm. Có thể dự đoán rằng kem sẽ được bán trong các tháng mùa hè nhiều hơn so với mùa đông và vì vậy có thể sử dụng đích khác nhau cho từng tháng. Việc không nhận biết dạng doanh thu và thay vào đó sử dụng giá trị không đổi cho các tháng sẽ dẫn đến đồ thị sai lệch trên giấy vẽ biểu đồ cusum. Giá trị cusum có khả năng tăng trong một khoảng thời gian của năm và sau đó giảm trong khoảng thời gian khác. Nếu đích đã được thay đổi, cusum sẽ được chuẩn bị tốt hơn để chỉ ra việc có bất kỳ thay đổi đáng kể nào về mức doanh thu kem hay không nếu loại bỏ “tính thời vụ”.
Giá trị đích không thích hợp có thể dẫn đến hiện tượng “thăng giáng” mô tả trong 9.1.5 và do đó cần xem xét cẩn thận khi lựa chọn đích loại này.
Chuẩn mực đối với cách tiếp cận giá trị đã cho được sử dụng khi theo dõi trung bình hoặc mức trung bình (vị trí) đối với tham số hoặc đặc trưng đang xét. Mặc dù có thể sử dụng cách tiếp cận tương tự để thiết lập giá trị đích cho việc theo dõi độ biến động (phân tán) như độ lệch chuẩn nhóm con hoặc độ rộng, nhưng thực tế này không được khuyến nghị trong TCVN 9945 (ISO 7870). Ưu tiên tiến hành bằng cách sử dụng hướng dẫn trong 9.2.3 và điều sau đó.
9.2.3. Đích dựa trên hiệu năng
Giá trị đích có thể được thiết lập từ các mức hiệu năng hiện tại. Cách tiếp cận này phù hợp với biểu đồ kiểm soát dựa trên hiệu năng trong đó kiểm soát được thiết lập theo hiệu năng của tham số quá trình hoặc đặc trưng sản phẩm gần đây.
Để theo dõi vị trí hoặc sự phân tán, điều thiết yếu là thu thập dữ liệu trong giai đoạn “thử nghiệm” hoặc “thu thập dữ liệu”. Khoảng thời gian này cần đủ dài để theo dõi đầy đủ độ biến động vốn có và đây sẽ là đối tượng đánh giá. Thông thường, phép thử cần đủ dài để đưa ra 25 điểm trên đồ thị cusum. Từ dữ liệu này, cần ước lượng giá trị trung bình và độ lệch chuẩn.
Khi đã xác định được, cần sử dụng các giá trị đích này cho việc tính cusum nhưng có thể cần thay đổi tại thời điểm sau đó nếu cusum chỉ ra thay đổi về mức. Nếu không thể đưa ra bất kỳ điều chỉnh quá trình nào sau thay đổi như vậy, hoặc nếu mức mới chấp nhận được, thì hành động duy nhất có thể thực hiện là thay đổi giá trị đích. Điều này thường được thực hiện sau khi đánh giá mới từ dữ liệu mới nhất và lấy nó làm đích mới. Sau đó cusum sẽ theo dõi tham số hoặc đặc trưng so với giá trị đích mới của nó.
9.3. Chương trình cusum đối với việc theo dõi vị trí
9.3.1. Chương trình chuẩn
Xem Hình 12.
Bước 1 – Xác định đối tượng lập biểu đồ cusum
Xác định tham số quá trình hoặc đặc trưng sản phẩm cần theo dõi.
CHÚ THÍCH 1: Đây có thể là hướng dẫn từ khách hàng hoặc tham số quá trình chính hoặc đặc trưng sản phẩm quan trọng. Đối tượng cũng có thể được xác định trong quá trình thực hiện giải quyết vấn đề.
Bước 2 – Xác định cỡ nhóm con
Xác định nhóm con hợp lý đối với biểu đồ cusum là quá trình tư duy đồng nhất được sử dụng để xây dựng bất kỳ biểu đồ Shewhart nào.
Nếu tham số quá trình là đối tượng cusum được lựa chọn, cỡ nhóm con thích hợp nhất thường là một. Điều này là do các tham số, ví dụ: nhiệt độ của dung dịch hay áp lực trong bình không có khả năng thay đổi trong thời gian ngắn. Thực hiện một vài phép đo lặp lại liên tục tiếp nối nhau không có khả năng thể hiện bất kỳ sự khác biệt nào trong phép đo. Điều này sẽ dẫn đến các vấn đề kỹ thuật khi xác định độ lệch chuẩn và thiết lập chính xác mặt nạ cusum.
Nếu thực sự dữ liệu cùng một thời gian, chẳng hạn như giá trị doanh thu cho một tháng cụ thể, thì cỡ nhóm con hợp lý sẽ là một.
Khi đã lựa chọn đặc trưng sản phẩm, cỡ nhóm con hợp lý thường lớn hơn một và thường là năm. Cần thực hiện theo hướng phổ biến ở đây. Cỡ nhóm con cũng được lựa chọn để thể hiện độ biến động ngẫu nhiên trong quá trình.
Bước 3 – Lựa chọn chương trình cusum
Bảng 9 cho thấy bộ chương trình chuẩn đưa ra một loạt các yêu cầu điển hình về chương trình cusum. Bảng đưa ra hai chương trình cơ bản, một chương trình đưa ra độ dài trung bình của loạt mẫu (ARL) khá dài tại dịch chuyển bằng “không”, là chương trình CS1, và một chương trình còn lại ARL ngắn hơn, là chương trình CS2. Nói cách khác, chương trình CS2 sẽ phát hiện dịch chuyển trong mức quá trình nhanh hơn chương trình CS1 tương ứng, nhưng tại mức chi phí cho nhiều “báo hiệu sai” hơn. Người chịu trách nhiệm lựa chọn chương trình phải xác định tình huống nào là quan trọng hơn và từ đó lựa chọn chương trình thích hợp. Bảng 10 minh họa sự khác biệt về hiệu năng của chương trình chuẩn hóa này.
Bảng 9 – Chương trình cusum chuẩn đối với trung bình nhóm con
|
Sự dịch chuyển quan trọng về trung bìnha cần phát hiện |
Chương trình CS1 |
Chương trình CS2 |
||
|
h |
¦ |
h |
¦ |
|
|
i) <>se |
8,0 |
0,25 |
5,0 |
0,25 |
|
ii) 0,75 đến 1,50se |
5,0 |
0,50 |
3,5 |
0,50 |
|
iii) > 1,50se |
2,5 |
1,00 |
1,8 |
1,00 |
|
CHÚ THÍCH 1: Chương trình CS1 cho độ dài trung bình của loạt mẫu, L0, trong khoảng 700 đến 1000 khi sự dịch chuyển thực tế bằng “không“. CHÚ THÍCH 2: Chương trình CS2 cho độ dài trung bình của loạt mẫu, L0, trong khoảng 140 đến 200 khi sự dịch chuyển thực tế bằng “không“. |
||||
|
a Đối với các kết quả riêng lẻ (cỡ nhóm con = 1), se thể hiện độ lệch chuẩn. Khi cỡ nhóm con lớn hơn một, se thể hiện sai số chuẩn của trung bình. |
||||
Khi đã đưa ra quyết định lựa chọn CS1 hay CS2, quyết định tiếp theo là về mức độ của dịch chuyển quan trọng. Ba cấp dịch chuyển điển hình được đưa ra trong bảng. Tùy theo lựa chọn này giá trị đối với h và ¦ có thể được đọc từ bảng.
Nếu không rõ nên chọn chương trình nào, thông lệ và thực tế cho thấy chương trình khởi đầu tốt là chọn chương trình CS1 ii), nghĩa là h = 0,5 và ¦ = 0,50.
Bảng 10 – So sánh hiệu năng của chương trình cusum chuẩn đối với trung bình nhóm con
Các giá trị là độ dài trung bình của loạt mẫu (ARL)
|
Dịch chuyển về trung bình từ giá trị đích (theo đơn vị se)a |
Chương trình CS1 |
Chương trình CS2 |
||||
|
(i) |
(ii) |
(iii) |
(i) |
(ii) |
(iii) |
|
|
0,00 |
730,0 |
930,0 |
715,0 |
140,0 |
200,0 |
170,0 |
|
0,75 |
16,4 |
17,0 |
27,0 |
10,5 |
11,5 |
15,0 |
|
1,00 |
11,4 |
10,5 |
13,4 |
7,4 |
7,4 |
8,8 |
|
1,50 |
7,1 |
5,8 |
5,4 |
4,7 |
4,3 |
4,0 |
|
CHÚ THÍCH: Các giá trị được cho là ARL. Người đọc cần biết rằng độ dài trung bình của loạt mẫu thực tế được lấy để phát hiện sự dịch chuyển thực tế sẽ thay đổi và có thể ngắn hơn hoặc dài hơn ARL. Khi điều này được quan tâm đặc biệt, người đọc cần kiểm tra phân bố của độ dài loạt đối với sự dịch chuyển cụ thể từ đích để biết độ rộng dự kiến của độ dài loạt có thể có. |
||||||
|
a Đối với các kết quả riêng lẻ (cỡ nhóm con = 1), se thể hiện độ lệch chuẩn. Khi cỡ nhóm con lớn hơn một, se thể hiện sai số chuẩn của trung bình. |
||||||
Cho dù chương trình nào được lựa chọn, giá trị đối với các tham số này cần được nhân với độ biến động ước lượng, s (hoặc se), để xác định cỡ thực tế và hình dạng của mặt nạ. Điều này được mô tả trong Bước 8.

Hình 12 – Lưu đồ xây dựng cusum
Bước 4 – Thu thập dữ liệu giai đoạn thử
Như đã nêu trong 9.2.3, dữ liệu cần thu thập sẽ mô tả tính chất của độ biến động trong quá trình, vì vậy chương trình cusum có thể được “điều chỉnh“ thích hợp và hỗ trợ việc thiết lập giá trị đích nếu cần.
Xác định giai đoạn thử trong đó tất cả các nguồn biến động của quá trình sẽ được theo dõi. Giai đoạn này cần đủ dài hoặc tần số lấy mẫu đủ lớn để tạo ra ít nhất 25 nhóm con dữ liệu.
Chú ý không đưa ra nguồn biến động bổ sung, ví dụ: điều chỉnh quá trình, trong giai đoạn này vì điều này làm thay đổi dạng biến động. Nếu có sự gián đoạn trong thu thập dữ liệu, cần đưa ra quyết định là giai đoạn thử có cần phải thực hiện lại hay không hoặc đã có đủ dữ liệu trong giai đoạn thử rút ngắn hay chưa. Nhìn chung, nếu số lượng nhóm con được thu thập là 20 hoặc nhiều hơn và nếu xét thấy tất cả các nguồn biến động tiềm ẩn được quan sát trong 20 nhóm con thì số lượng nhóm con này sẽ là thỏa mãn và kết thúc giai đoạn thử. Sau đó, cần sử dụng dữ liệu từ giai đoạn thử để thiết lập các mức biến động mà chương trình cusum sẽ hoạt động. Điều này được mô tả trong Bước 5 và 6.
Bước 5 – Ước lượng se từ dữ liệu giai đoạn thử
a) Khái quát
Các đoạn dưới đây đưa ra phương pháp ước lượng se. Trường hợp đặc biệt có thể xảy ra khi cần một cách tiếp cận khác. Cách tiếp cận khác này có thể yêu cầu đánh giá se bằng cách xem xét độ lệch chuẩn giữa trung bình nhóm con.
b) Cỡ nhóm con lớn hơn một (n > 1)
i. Tính độ rộng của mỗi nhóm con (quan trắc lớn nhất trừ đi quan trắc nhỏ nhất).
ii. Tính độ rộng trung bình ![]() của tất cả các độ rộng nhóm con.
của tất cả các độ rộng nhóm con.
iii. Ước lượng độ lệch chuẩn trong nhóm con (s0) bằng cách chia độ rộng trung bình cho giá trị d2 thích hợp lấy từ Bảng 11.
iv. Ước lượng se bằng cách chia s0 cho căn bậc hai của cỡ nhóm con, nghĩa là se = s0 / ![]() .
.
Bảng 11 – Hệ số d2 để ước lượng độ lệch chuẩn trong nhóm con từ độ rộng trong nhóm con
|
Cỡ nhóm con, na |
d2 |
|
2 |
1,128 |
|
3 |
1,693 |
|
4 |
2,059 |
|
5 |
2,326 |
|
6 |
2,534 |
|
7 |
2,704 |
|
8 |
2,847 |
|
9 |
2,970 |
|
10 |
3,078 |
|
CHÚ THÍCH: Đối với các nhóm con lớn hơn 10 các phương pháp khác có thể hiệu quả hơn trong việc ước lượng độ lệch chuẩn trong nhóm con. |
|
|
a Có giá trị của d2 cho n > 10. Xem TCVN 9945-2 (ISO 7870-2) hoặc sách hay các tiêu chuẩn khác. |
|
Phương pháp độ lệch chuẩn trong nhóm con (s) có thể được dùng thay thế cho độ rộng nhóm con. Độ lệch chuẩn nhóm con trung bình, ![]() , phải được tính thay cho
, phải được tính thay cho ![]() và s0 được ước lượng bằng
và s0 được ước lượng bằng ![]() .
.
Bảng 18 có giá trị của c4.
c) Cỡ nhóm con là một (n = 1)
Cách tiếp cận được thực hiện để ước lượng se là sử dụng phương pháp hiệu liên tiếp (đôi khi được gọi là độ rộng trượt của hai quan trắc).
Dữ liệu thu thập trong giai đoạn thử cần được sắp xếp theo trình tự thu thập chúng. Cần tính độ rộng (hiệu) giữa kết quả đầu tiên và kết quả thứ hai, sau đó là độ rộng giữa kết quả thứ hai và thứ ba, v.v… Nếu có k nhóm con thì sẽ có k – 1 độ rộng. Tính trung bình của độ rộng này ![]() .
.
Sau đó, có thể tìm ước lượng của se bằng cách chia độ rộng trung bình cho 1,128.
Bước 6 – Xác định giá trị đích, T
Như mô tả trong 9.2, giá trị đích có thể là giá trị đã cho hoặc giá trị dựa trên hiệu năng được xác định từ dữ liệu.
a) Giá trị đã cho
Giá trị đích là giá trị quy định. Có thể lấy giá trị này từ tài liệu quy định hoặc bản vẽ và có thể là giá trị danh nghĩa, trong trường hợp đặc trưng sản phẩm, hoặc một mức hiệu năng dự kiến do người quản lý đưa ra trong trường hợp quá trình phi sản xuất.
b) Giá trị dựa trên hiệu năng
Ở đây, cần xác định giá trị đích từ dữ liệu thu được trong giai đoạn thử.
i. Tính giá trị trung bình (![]() ) cho mỗi nhóm con.
) cho mỗi nhóm con.
ii. Tính trung bình (![]() ) của các trung bình nhóm con.
) của các trung bình nhóm con.
iii. Gán ![]() là giá trị đích, T.
là giá trị đích, T.
Bước 7 – Thiết lập văn phòng phẩm cusum
a) Khái quát
Điều 5 đưa ra hướng dẫn về việc thiết lập văn phòng phẩm cusum.
b) Bảng cusum
Lập bảng thích hợp trong đó phép tính cusum được viết và tra từ đó. Một phần của bảng như vậy được thể hiện trong Bảng 12.
Bảng 12 – Bảng tính cusum
|
Số nhóm con |
|
|
Giá trị cusum, C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v.v… |
|
|
|
Nếu cỡ nhóm con là một, thay ![]() bằng x, kết quả riêng trong bảng.
bằng x, kết quả riêng trong bảng.
c) Giấy vẽ đồ thị cusum
Chọn giấy vẽ đồ thị có khoảng giữa các đường lưới thích hợp. Lựa chọn sẽ tùy thuộc vào mục đích sử dụng giấy dự kiến, ví dụ: treo tường hoặc hiển thị công khai.
Chọn thang đo thích hợp. Thang đo sẽ chịu ảnh hưởng bởi vị trí của đồ thị. Ví dụ, đối với đồ thị dùng trên tường hoặc hiển thị công khai, khoảng cách giữa số nhóm con trên trục hoành có thể là 10 mm, trong khi đối với đồ thị dùng trên bàn, chỉ sử dụng khoảng cách là 5 mm.
Khoảng thích hợp đối với trục (C) cusum được cho bằng cách chọn khoảng cách tương tự cho trục hoành xấp xỉ bằng 2se, làm tròn khi thích hợp. Việc chia thang đo này không có khả năng “san bằng” xu hướng quan trọng hoặc phóng đại xu hướng không quan trọng.
Đánh dấu điểm tâm của trục cusum 0 và vẽ một đường nằm ngang đậm nét trên giấy vẽ đồ thị qua điểm này. Đánh dấu ngoài thang đo cusum thẳng đứng trên giấy vẽ đồ thị.
Ví dụ về giấy vẽ được thể hiện trên Hình 13.
Bước 8 – Lập mặt nạ cusum
8.2.1. mô tả hình dạng của mặt nạ cusum chuẩn và Hình 5 minh họa các thành phần của mặt nạ và cách chia tỷ lệ.
Cần xác định giá trị h, ¦ và se như mô tả trong điều này.
a) Tính H = hse
b) Tính F = ¦se
Mặt nạ cần được vẽ theo thang đo lựa chọn đối với giấy vẽ cusum. Điều này là thiết yếu nếu mặt nạ được sử dụng chính xác để đưa ra quyết định xem sự thay đổi có mức độ xác định trước đã xảy ra chưa.
CHÚ THÍCH 2: Một số mặt nạ được làm từ nguyên liệu trong suốt như axêtat. Hình dáng của mặt nạ có thể tìm được bằng cách sử dụng mực không xóa được. Đôi khi mặt nạ có thể được cắt ra từ một miếng thẻ, giá trị H và F cũng được đánh dấu bằng cách sử dụng thang đo của giấy vẽ cusum.
CHÚ THÍCH 3: Chương trình máy tính hiện có sẽ hiển thị đồ thị cusum với mặt nạ được vẽ trên máy tính, tất cả đều chia tỷ lệ tự động.
Bước 9 – Tính cusum cho dữ liệu thử
Sử dụng giá trị đích xác định trong Bước 6 và bảng tương tự như thể hiện trong Bảng 12, tính giá trị cusum cho dữ liệu thử.
Bước 10 – Vẽ cusum cho dữ liệu thử
Giá trị cusum bảng thu được như đề cập ở trên cần được vẽ trên giấy đồ thị thích hợp tương tự như thể hiện trên Hình 13, đồ thị bắt đầu từ bên trái và mở rộng theo hướng sang phải. Nối tất cả các điểm được vẽ vì điều này làm cho dễ nhận biết mọi xu hướng hơn và sau đó, khi mặt nạ được đặt lên trên, nó giúp nhận biết báo hiệu mất kiểm soát.
Bước 11 – Xem xét đồ thị cusum của dữ liệu thử về sự mất kiểm soát
Đặt chồng mặt nạ lên trên đồ thị cusum.
Thực hiện việc này bằng cách xác định vị trí “điểm dẫn” được chỉ ra trên Hình 7 a) đến giá trị cusum được vẽ cuối cùng, cần chú ý giữ điểm tâm của mặt nạ song song với trục “không” trên giấy vẽ. Điều này đảm bảo mặt nạ được định hướng chính xác.
Mọi điểm ở phía ngoài cạnh (đường quyết định) của mặt nạ đều cho thấy sự có mặt của quá trình mất kiểm soát, ngay cả khi điểm vi phạm không phải là điểm được vẽ cuối cùng và ngay cả nếu các điểm được vẽ sau đó trở lại phía trong cạnh của mặt nạ. Xem Hình 7 b).

Hình 13 – Ví dụ giấy vẽ cusum
Bước 12 – Xác định và loại bỏ “nguyên nhân đặc biệt“
a) Khái quát
Điều thiết yếu là nghiên cứu bất kỳ điểm mất kiểm soát nào trên đồ thị cusum và xác định “nguyên nhân đặc biệt”.
b) “Nguyên nhân đặc biệt” được xác định và ngăn ngừa tái diễn
Khi nguyên nhân đặc biệt đã được xác định và các bước đã được thực hiện để ngăn ngừa biến cố trong tương lai, có thể cần sửa đổi giá trị đích và sai số chuẩn (hoặc độ lệch chuẩn). Nếu chỉ một điểm mất kiểm soát được quan sát và nguyên nhân đã được xử lý thỏa đáng, thì có thể sửa đổi giá trị được gán là đích trước đó và sai số chuẩn hoặc độ lệch chuẩn bằng cách sử dụng dữ liệu giai đoạn thử ban đầu nhưng không tính dữ liệu đối với nhóm mất kiểm soát. Xét lại các tính toán đối với cách chia tỷ lệ của giấy vẽ đồ thị cusum và kích thước của mặt nạ, lập lại thang đo trên giấy và mặt nạ khi cần.
Nếu có một số điểm mất kiểm soát trong dữ liệu thử, thì điều đó cho biết có nhiều vấn đề hơn trong quá trình và nên xem xét lại, điều chỉnh quá trình, sau đó bắt đầu giai đoạn thử mới và lặp lại tiến trình thiết lập cusum với các dữ liệu mới này.
c) “Nguyên nhân đặc biệt” được nhận biết nhưng không được ngăn ngừa việc tái diễn
Có một số trường hợp không thể ngăn ngừa nguyên nhân đặc biệt trong tương lai do không kinh tế hoặc cân nhắc về kỹ thuật.
Trong những trường hợp đó, các tham số cusum dựa trên tất cả dữ liệu thử và được sử dụng cho việc theo dõi tiếp theo. Nói cách khác, các nguyên nhân đặc biệt này được coi là một phần độ biến động ngẫu nhiên của quá trình.
d) “Nguyên nhân đặc biệt” không được nhận biết
Đôi khi “nguyên nhân đặc biệt” có thể vẫn chưa được xác định. Điều này luôn không thỏa đáng vì nó ngăn ngừa cải tiến quá trình. Cần phải thực hiện mọi nỗ lực để nghiên cứu nguyên nhân đặc biệt, sử dụng thống kê và kỹ thuật giải quyết vấn đề khác để thực hiện điều này. Các kỹ thuật như thiết kế thống kê thực nghiệm đặc biệt hiệu quả đối với vấn đề này.
Nếu các nguyên nhân đặc biệt vẫn không được xác định, thực hiện các bước như nêu trong c) ở trên.
Bước 13 – Tiếp tục lập biểu đồ
a) Khái quát
Nếu dữ liệu thử đưa ra tình huống “được kiểm soát” hoặc khi dữ liệu mới được thu thập sau khi giải quyết thỏa đáng “nguyên nhân đặc biệt”, thì cusum đã sẵn sàng cho việc theo dõi liên tục tham số quá trình hoặc đặc trưng sản phẩm. Lúc này, sử dụng thang đo trên giấy, tham số mặt nạ và thang đo mặt nạ để theo dõi dữ liệu từ các nhóm con về sau.
Nếu các báo hiệu mất kiểm soát tương lai xuất hiện, cần phải nghiên cứu và quyết định hành động nào cần thực hiện đối với quá trình. Điều này có thể bao gồm từ điều chỉnh quá trình, như trên công cụ, đến áp dụng giá trị đích mới nếu quá trình đã dịch chuyển đến vị trí mong muốn hơn.
b) Điều chỉnh quá trình
Có thể xác định lượng điều chỉnh cần thiết từ đồ thị cusum.
i. Xác định giá trị cusum đối với điểm được vẽ cuối cùng.
ii. Xác định giá trị cusum tại nơi mà đồ thị cusum nằm ngoài cạnh hành động trên mặt nạ. Trong trường hợp có nhiều vi phạm, lấy giá trị gần nhất, nghĩa là điểm mất kiểm soát nằm gần điểm đầu nhất trên mặt nạ.
iii. Tính chênh lệch giá trị cusum giữa hai điểm này.
iv. Đếm số điểm được vẽ trên đồ thị giữa điểm ở đỉnh trên mặt nạ và điểm mất kiểm soát.
v. Chia chênh lệch được tính trong iii) cho số điểm vẽ đồ thị đếm được ở iv), nghĩa là tính độ dốc cục bộ của đồ thị cusum. Đây là ước lượng sự dịch chuyển từ giá trị đích mà quá trình đi qua.
vi. Có thể thực hiện điều chỉnh quá trình với cùng độ lớn. Ghi trên đồ thị cusum về những thay đổi đã thực hiện.
vii. Trả giá trị cusum về “không” và tiếp tục theo dõi.
CHÚ THÍCH 4: Thay vì thực hiện tính toán mô tả ở đây, do tính chất hình học của mặt nạ và giấy vẽ cusum, có thể tạo đồ thị “tra cứu” để đọc lượng dịch chuyển khỏi đích. Có thể thấy ví dụ này trong Hình 14.

Hình 14 – Ví dụ vẽ đồ thị tra cứu đối với sự dịch chuyển khỏi đích
c) Điều chỉnh quá trình – chống sự thăng giáng
Khái niệm “thăng giáng” được giới thiệu trong 9.1.5. Áp dụng các phương pháp cusum cho thấy điều chỉnh quá trình đối với 100 % sự dịch chuyển tính được so với đích có thể tạo ra sự thăng giáng. Tiếp theo điều chỉnh đó cusum cho thấy nhu cầu điều chỉnh tiếp quá trình, nhưng theo hướng ngược lại, nghĩa là sự điều chỉnh quá nhiều. Nếu lúc này quá trình được điều chỉnh lại một lượng bằng sự dịch chuyển được chỉ thị gần nhất thì sau đó có thể là điều chỉnh nhiều hơn theo hướng ngược lại. Hiện tượng này được gọi là “thăng giáng”.
Hiện tượng này có thể là do độ dốc cusum ngắn hạn phóng đại sự dịch chuyển thực tế có thể xử lý bằng cách thay đổi thiết kế mặt nạ, hoặc do không thể đạt được điều chỉnh thực tế cần thiết.
Một giải pháp thực tiễn là điều chỉnh quá trình ít hơn 100 % sự dịch chuyển mặc nhiên. Phần trăm ít hơn này được gọi là “hệ số chống thăng giáng”. Điều này làm giảm xu hướng của cusum đối với “sự thăng giáng”. Thông lệ và thực tiễn cùng với nghiên cứu cho thấy hệ số chống thăng giáng 75 % là thích hợp. Do đó, khuyến nghị, ít nhất là lần đầu, chỉ điều chỉnh về 75 % sự dịch chuyển mặc nhiên.
Có thể vẽ đồ thị như thể hiện trong Hình 14 theo cách kết hợp hệ số chống thăng giáng. Đây có thể là mong muốn nếu có nhiều người tham gia vào vận hành hệ thống cusum.
Hệ số chống thăng giáng khác là r/(r +1), trong đó r là số điểm giữa điểm dẫn và điểm mất kiểm soát. Sử dụng hệ số này, cỡ điều chỉnh quá trình, j, được tính như sau:
![]()
trong đó Cr là chênh lệch giá trị cusum giữa điểm dẫn và điểm mất kiểm soát. Khi xảy ra thay đổi theo nấc, phương pháp này có hiệu năng tốt để ngăn ngừa sự thăng giáng.
9.3.2. Chương trình chuẩn – Hạn chế
Chương trình cusum cơ bản được mô tả trong 9.3.1 đưa ra vị trí khởi đầu tốt cho hầu hết các ứng dụng và trong nhiều trường hợp sẽ không cần thêm bất kỳ sự thay đổi nào. Mặc dù đối với một vài ứng dụng, sau một thời gian có thể nhận thấy cần cải tiến chương trình cơ bản được lựa chọn vì ARL phát hiện sự dịch chuyển đáng kể là quá lớn hoặc tần số “báo động sai” quá cao.
9.3.3. Chương trình cusum “điều chỉnh”
CHÚ THÍCH: Thiết kế chương trình cusum cụ thể yêu cầu sự hiểu biết và đầu vào nhiều hơn chương trình cơ bản được mô tả trong 9.3.1. Bất kỳ ai yêu cầu chương trình cusum có thể mong muốn tham khảo ý kiến chuyên gia để hỗ trợ việc thiết kế.
a) Xác định mức độ dịch chuyển (quan trọng) từ đích cần được phát hiện, d.
b) Ước lượng sai số chuẩn, se, (hoặc độ lệch chuẩn nếu cỡ nhóm con là một) như được mô tả trước đó.
c) Quy định ARL dự kiến khi sự dịch chuyển có mức nêu trong 9.3.1 Bước 3, Ld.
d) Quy định ARL dự kiến khi sự dịch chuyển bằng “không”, nghĩa là tần số “báo động sai”, L0.
e) Tính sự dịch chuyển chuẩn hóa, D = d/se.
f) Điền vào đồ thị trong Hình 15 và tra h đối với giá trị D tính được và tính đến các giá trị cho Ld và L0.
g) Cũng có thể đọc giá trị ¦ từ đồ thị tương ứng với giá trị D tính được.
h) Sửa đổi mặt nạ cusum theo các giá trị mới cho h và ¦ như đã nêu trước đó.
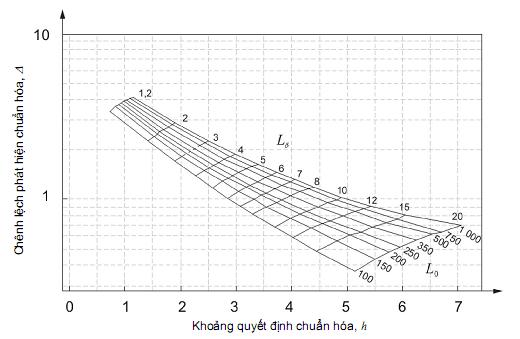
Hình 15 – Biểu đồ chắn đối với các tham số mặt nạ (giả định biến chuẩn)
9.4. Chương trình cusum dùng cho theo dõi độ biến động
9.4.1. Khái quát
Ngoài việc theo dõi vị trí quá trình, cần phải theo dõi độ biến động của quá trình, trong nhiều trường hợp là biến động ngắn hạn.
Hai thước đo độ biến động thích hợp nhất để sử dụng là độ rộng trong nhóm con và độ lệch chuẩn trong nhóm con. Cần đưa ra lựa chọn sử dụng loại nào. Quyết định đó sẽ phụ thuộc vào việc dễ tính toán và mức độ hiểu biết về thước đo từ phía những người tham gia tính. Những người sử dụng biểu đồ kiểm soát chọn độ rộng là thước đo ưu tiên vì sự dễ dàng trong tính toán và tính đơn giản của nó, cỡ đối với nhóm con thường được chọn, ví dụ: năm mẫu, hiệu quả của độ rộng tốt gần như độ lệch chuẩn.
Nếu cỡ nhóm con là một, thước đo cần sử dụng là độ rộng dựa trên hiệu giữa các kết quả liên tiếp.
9.4.2. Chương trình cusum đối với độ rộng nhóm con
Cần tuân theo các bước sau đây để thiết lập chương trình thích hợp cho việc theo dõi độ biến động quá trình bằng cách sử dụng độ rộng trong nhóm con. Một trong số các bước đã được hoàn tất nếu chương trình cusum theo dõi giá trị trung bình đã được thực hiện.
Bước 1 – Xác định đối tượng cho việc lập biểu đồ cusum
Tham khảo 9.3.1 Bước 1.
Bước 2 – Xác định cỡ nhóm con
Tham khảo 9.3.1 Bước 2.
Bước 3 – Lựa chọn chương trình cusum đối với độ rộng
Bảng 13 quy định bộ chương trình chuẩn đưa ra các yêu cầu điển hình cho chương trình cusum đối với độ rộng. Như được mô tả trong 9.3.1, bảng đưa ra hai chương trình cơ bản, một chương trình cho độ dài trung bình của loạt mẫu (ARL) khá dài ở mức biến động dự kiến, nghĩa là chương trình CS1, và chương trình còn lại có ARL ngắn hơn, nghĩa là chương trình CS2. Chương trình CS2 sẽ phát hiện sự dịch chuyển mức quá trình nhanh hơn chương trình CS1 tương ứng, nhưng ở chi phí cho nhiều “báo hiệu sai”. Bảng 4 minh họa sự khác biệt về hiệu năng của hai chương trình chuẩn này.
Bảng 13 – Chương trình cusum chuẩn đối với độ rộng nhóm con
|
Cỡ nhóm con |
Chương trình CS1 |
Chương trình CS2 |
||
|
h |
¦ |
h |
¦ |
|
|
2 3 4 5 6 7 8 9 10 |
2,50 1,75 1,25 1,00 0,85 0,70 0,55 0,55 0,50 |
0,85 0,55 0,50 0,45 0,45 0,45 0,40 0,40 0,35 |
2,50 1,75 1,25 1,00 0,85 0,70 0,55 0,55 0,50 |
0,55 0,35 0,30 0,30 0,30 0,30 0,25 0,25 0,25 |
|
CHÚ THÍCH 1: Chương trình CS1 cho độ dài trung bình của loạt mẫu, L0, trong khoảng 600 đến 1 000 khi quá trình hoạt động ở mức biến động dự kiến. CHÚ THÍCH 2: Chương trình CS2 cho độ dài trung bình của loạt mẫu, L0, trong khoảng 150 đến 210 khi quá trình hoạt động ở mức biến động dự kiến. |
||||
Lựa chọn chương trình CS1 hoặc CS2. Cần áp dụng chuẩn mực lựa chọn tương tự sử dụng trong lựa chọn chương trình trung bình nhóm con. Nếu cần ARL dài hơn khi không có sự thay đổi nào xảy ra thì chọn chương trình CS1; nếu không thì chọn chương trình CS2.
Dù lựa chọn chương trình nào, giá trị các tham số này cần được nhân với độ biến động ước lượng ![]() để xác định cỡ thực tế và hình dạng của mặt nạ. Điều này được mô tả trong Bước 8.
để xác định cỡ thực tế và hình dạng của mặt nạ. Điều này được mô tả trong Bước 8.
Bước 4 – Thu thập dữ liệu giai đoạn thử
Các hướng dẫn về vị trí cũng áp dụng ở đây.
Bước 5 – Ước lượng ![]() từ dữ liệu giai đoạn thử
từ dữ liệu giai đoạn thử
Tính ![]() bằng cách sử dụng một trong những phương pháp được mô tả trong 9.3.1 Bước 5.
bằng cách sử dụng một trong những phương pháp được mô tả trong 9.3.1 Bước 5.
Bảng 14 – So sánh hiệu năng (ARL) của các chương trình cusum chuẩn đối với độ rộng nhóm con
|
Cỡ nhóm con |
Mức biến động quá trình thực tế |
Chương trình CS1 |
Chương trình CS2 |
|
2 |
2 4 |
779,0 7,2 2,3 |
170,0 5,5 2,1 |
|
3 |
2 4 |
893,0 4,5 1,6 |
196,0 3,6 1,5 |
|
4 |
2 4 |
918,0 3,3 1,3 |
157,0 2,7 1,2 |
|
5 |
2 4 |
771,0 2,7 1,2 |
179,0 2,3 1,1 |
|
6 |
2 4 |
942,0 2,4 1,1 |
204,0 2,0 1,1 |
|
8 |
2 4 |
893,0 2,0 1,0 |
162,0 1,7 1,0 |
|
10 |
2 4 |
635,0 1,7 1,0 |
184,0 1,5 1,0 |
|
CHÚ THÍCH: Các giá trị được cho là ARL. Người đọc cần biết rằng độ dài trung bình của loạt thực tế được lấy để phát hiện thay đổi thực tế sẽ khác nhau và có thể ngắn hơn hoặc dài hơn ARL. Khi điều này được quan tâm đặc biệt, người đọc cần kiểm tra phân bố của độ dài loạt đối với dịch chuyển cụ thể từ đích để biết độ rộng dự kiến của độ dài loạt có thể có. |
|||
Bước 6 – Xác định giá trị đích, T
a) Giá trị đã cho
Trong kiểm soát chất lượng thống kê hoặc quá trình, phương pháp phổ biến nhất về thiết lập độ rộng đích được mô tả trong điểm b) dưới đây. Tuy nhiên, có thể có những trường hợp ưu tiên thiết lập đích từ một mức giả định nào đó. Nếu vậy, độ rộng đích được đưa ra bằng giá trị độ rộng đã cho.
Nếu độ biến động được mô tả thông qua độ lệch chuẩn đã cho thì có thể tính độ rộng đích T = d2s trong đó d2 có thể lấy từ Bảng 11, giá trị phụ thuộc vào cỡ nhóm con được sử dụng.
b) Giá trị dựa trên hiệu năng
Từ dữ liệu thu được trong giai đoạn thử đặt độ rộng đích bằng ![]() .
.
Bước 7 – Thiết lập văn phòng phẩm cusum
Lập bảng cusum (hoặc bổ sung vào bảng cusum hiện có) và xây dựng giấy vẽ đồ thị cusum như mô tả trong 9.3.1 Bước 7.
Giấy vẽ đồ thị cusum trong đó cusum cho độ rộng được vẽ đồ thị có thể cần thang đo khác với thang đo được chọn để theo dõi giá trị trung bình. Có thể có thang đo thích hợp bằng cách sử dụng phép tính sau, làm tròn lên hoặc xuống đối với giá trị thuận lợi gần nhất.
Khoảng thang đo cusum với độ rộng là a![]() , trong đó a được lấy từ Bảng 15.
, trong đó a được lấy từ Bảng 15.
Bảng 15 – Giấy vẽ đồ thị cusum cho hệ số thang đo độ rộng
|
Cỡ nhóm con |
a |
|
2 3 4 5 6 8 10 |
1,50 1,00 0,85 0,75 0,65 0,55 0,50 |
Bước 8 – Lập mặt nạ cusum
Sử dụng giá trị h và ¦ được chọn trong Bước 3, tính:
a) H = h![]() ; và
; và
b) F = ¦![]() .
.
Xây dựng mặt nạ bằng cách sử dụng giá trị H và F tính được và chia thang đo mặt nạ theo thang đo được chọn cho giấy vẽ đồ thị cusum.
Bước 9 – Tính cusum đối với dữ liệu thử
Sử dụng giá trị đích xác định trong Bước 6 và sử dụng bảng tương tự như Bảng 12, tính các giá trị cusum cho độ rộng đối với dữ liệu thử.
Bước 10 – Vẽ cusum cho dữ liệu thử
Vẽ cusum độ rộng trên giấy vẽ đồ thị cusum đối với độ rộng mô tả trong 9.3.1 Bước 7 và Bước 10.
Bước 11 – Xem xét đồ thị cusum của dữ liệu thử về tính mất kiểm soát
Xem xét đồ thị cusum như mô tả trong 9.3.1 Bước 11.
Bước 12 – Xác định và loại bỏ “nguyên nhân đặc biệt”
a) Khái quát
Điều thiết yếu là kiểm tra mọi điểm mất kiểm soát trên đồ thị cusum và nhận biết “nguyên nhân đặc biệt”.
Nếu cần sửa đổi độ rộng đích theo một trong các điều nhỏ dưới đây, thì cũng cần sửa đổi mặt nạ và có thể là giấy vẽ đồ thị cusum đối với kiểm soát giá trị trung bình.
b) “Nguyên nhân đặc biệt” được xác định và ngăn ngừa tái diễn
Khi nguyên nhân đặc biệt đã được xác định và thực hiện các bước để ngăn ngừa biến cố như vậy trong tương lai, giá trị độ rộng đích có thể cần xem xét lại. Nếu chỉ quan sát được một điểm mất kiểm soát và giải quyết thỏa đáng như mô tả trong điểm a), thì có thể sửa đổi giá trị được gán cho đích trước đó bằng cách sử dụng dữ liệu giai đoạn thử ban đầu bằng cách loại bỏ dữ liệu đối với nhóm con mất kiểm soát. Xem lại cách tính đối với việc chia thang đo của giấy vẽ đồ thị cusum và kích thước của mặt nạ đồng thời thay đổi tỷ lệ giấy và mặt nạ khi cần.
Nếu có một số điểm mất kiểm soát trong dữ liệu thử thì điều đó chỉ ra có nhiều vấn đề hơn với quá trình. Khuyến nghị xem xét, điều chỉnh quá trình và sau đó bắt đầu giai đoạn thử mới và lặp lại tiến trình thiết lập cusum với dữ liệu mới này.
c) “Nguyên nhân đặc biệt” được xác định nhưng không được ngăn ngừa tái diễn
Có một số trường hợp không thể ngăn ngừa nguyên nhân đặc biệt trong tương lai do các trường hợp phi kinh tế hoặc cân nhắc kỹ thuật.
Trong các trường hợp đó, các tham số cusum dựa trên tất cả dữ liệu thử và được sử dụng cho việc theo dõi liên tục. Nói cách khác, các nguyên nhân đặc biệt này được coi là một phần của độ biến động ngẫu nhiên của quá trình.
d) “Nguyên nhân đặc biệt” không được nhận biết
Nếu các nguyên nhân đặc biệt vẫn chưa được nhận biết, cần phải theo các bước trong điểm c).
Điều này luôn không thỏa đáng vì nó ngăn ngừa cải tiến quá trình. Cần phải thực hiện mọi nỗ lực để nghiên cứu các nguyên nhân đặc biệt.
Bước 13 – Tiếp tục phân tích biểu đồ liên tục
a) Khái quát
Tiếp tục vẽ biểu đồ như quy định trong 9.3.1 Bước 13.
b) Các hoạt động quá trình
Như trong trường hợp theo dõi giá trị trung bình, nếu thấy báo hiệu mất kiểm soát, thì có thể ước lượng lượng thay đổi xảy ra trong độ dốc cusum. Trong trường hợp này, việc giải thích độ biến động đã thay đổi bao nhiêu, ở đây được thể hiện bằng ![]() , đã thay đổi.
, đã thay đổi.
Nếu hướng cusum cho thấy sự gia tăng độ rộng, phản ứng, trong trường hợp thiết bị, hoặc máy móc, có thể là yêu cầu kỹ sư bảo trì sửa chữa thiết bị. Nếu điều này thành công, cần ghi lại các hoạt động đã thực hiện, giá trị cusum điều chỉnh về “không” và quá trình được phép tiếp tục. Nếu quá trình trở lại mức biến động trước đó thì lúc này cusum sẽ hoạt động “trong tầm kiểm soát”.
Nếu hướng cusum cho thấy sự giảm độ rộng, nó thường được coi là biến cố tốt và cần nhận biết nguyên nhân đặc biệt và thực hiện các bước để duy trì. Nếu điều này thành công, cần điều chỉnh mặt nạ đối với cả trung bình và độ rộng (và có thể là giấy vẽ đồ thị) để phản ánh tình hình mới. Độ rộng đích cũng cần được đánh giá lại đối với giá trị dưới mới. Sau đó, cusum cho độ rộng cần được đặt lại về “không” trước khi tiếp tục vẽ đồ thị.
Không cần phải đặt lại cusum về “không” trung bình, mà từ việc xem xét bằng cách sử dụng mặt nạ điều chỉnh đối với trung bình của các điểm được vẽ trước đó trong giai đoạn thử, có thể thấy độ rộng đã thực sự thấp hơn. Lúc này, có thể quan sát các điểm mất kiểm soát mới đối với đồ thị trung bình.
c) Ước lượng độ biến động – chống thăng giáng
Như trong trường hợp cusum vị trí, nếu xét thấy cần sử dụng các thước đo chống thăng giáng, thì khuyến nghị giá trị đáp ứng 75 %. Do đó, chỉ nên lấy 75 % sự thay đổi được chỉ ra trong độ rộng đích.
9.4.3. Chương trình cusum đối với độ lệch chuẩn nhóm con
Quy trình thiết lập chương trình cusum để theo dõi độ lệch chuẩn rất giống với việc theo dõi độ rộng nhóm con. Do đó, chỉ những thay đổi so với 9.4.2 được nêu trong điều này và cần kết hợp với toàn bộ nội dung của 9.4.2.
Chương trình chi tiết trong điều này để theo dõi độ lệch chuẩn nhóm con phụ thuộc vào việc có nhiều hơn một quan trắc cho mỗi nhóm con. Ưu tiên phương pháp dựa trên độ rộng về sự khác biệt liên tiếp để theo dõi biến động nếu dữ liệu được thu thập là các giá trị tại một thời điểm, ví dụ: doanh số bán hàng hàng tháng.
Bước 3 – Lựa chọn chương trình cusum đối với độ lệch chuẩn
Bảng 16 quy định bộ chương trình chuẩn đưa ra các yêu cầu điển hình đối với chương trình cusum cho việc theo dõi độ lệch chuẩn. Bảng đưa ra hai chương trình cơ bản, một chương trình cho độ dài trung bình của loạt mẫu (ARL) khá dài ở mức biến động dự kiến, là chương trình CS1, và một chương trình còn lại có ARL ngắn hơn, là chương trình CS2. Chương trình CS2 đưa ra nhiều “báo hiệu sai” hơn chương trình CS1 nhưng sẽ phát hiện sự thay đổi quan trọng nhanh hơn chương trình CS1 tương ứng. Bảng 17 minh họa sự khác biệt về hiệu năng của hai chương trình chuẩn này.
Bảng 16 – Chương trình cusum chuẩn đối với độ lệch chuẩn nhóm con
|
Cỡ nhóm con |
Chương trình CS1 |
Chương trình CS2 |
||
|
h |
¦ |
h |
¦ |
|
|
2 3 4 4 5 6 7 8 9 10 12 15 20 |
2,00 1,60 1,15 1,15 0,90 0,80 0,70 0,60 0,55 0,50 0,40 0,35 0,30 |
0,50 0,35 0,35 0,35 0,35 0,32 0,30 0,30 0,30 0,30 0,30 0,27 0,23 |
2,00 1,60 1,15 1,15 0,90 0,80 0,70 0,60 0,55 0,50 0,40 0,35 0,30 |
0,25 0,15 0,20 0,20 0,20 0,20 0,20 0,20 0,20 0,20 0,20 0,18 0,16 |
|
CHÚ THÍCH 1: Chương trình CS1 cho độ dài trung bình của loạt mẫu, L0, trong khoảng 700 đến 1 000 khi quá trình hoạt động ở độ biến động dự kiến. CHÚ THÍCH 2: Chương trình CS2 cho độ dài trung bình của loạt mẫu, L0, trong khoảng 150 đến 200 khi quá trình hoạt động ở độ biến động dự kiến. |
||||
Chọn chương trình CS1 hoặc CS2. Cần áp dụng chuẩn mực lựa chọn tương tự trong lựa chọn chương trình đối với trung bình nhóm con. Nếu A cần RL dài hơn khi không có sự thay đổi nào xảy ra thì chọn chương trình CS1; nếu không thì chọn chương trình CS2.
Dù chọn chương trình nào thì giá trị đối với các tham số này cần được nhân với biến ước lượng ![]() để xác định cỡ và hình dạng thực tế của mặt nạ. Điều này được mô tả trong Bước 5 sau.
để xác định cỡ và hình dạng thực tế của mặt nạ. Điều này được mô tả trong Bước 5 sau.
Bảng 17 – So sánh hiệu năng (ARL) của chương trình cusum chuẩn đối với độ lệch chuẩn nhóm con
|
Cỡ nhóm con |
Mức biến động quá trình thực tế |
Chương trình CS1 |
Chương trình CS2 |
|
2 |
s0 |
920,0 |
185,0 |
|
2s0 |
7,4 |
5,6 |
|
|
4s0 |
2,3 |
2,1 |
|
|
3 |
s0 |
920,0 |
155,0 |
|
2s0 |
4,4 |
3,7 |
|
|
4s0 |
1,6 |
1,5 |
|
|
4 |
s0 |
840,0 |
180,0 |
|
2s0 |
3,2 |
2,6 |
|
|
4s0 |
1,3 |
1,2 |
|
|
5 |
s0 |
820,0 |
155,0 |
|
2s0 |
2,6 |
2,2 |
|
|
4s0 |
1,1 |
1,1 |
|
|
6 |
s0 |
850,0 |
190,0 |
|
2s0 |
2,2 |
1,9 |
|
|
4s0 |
<> |
<> |
|
|
8 |
s0 |
720,0 |
180,0 |
|
2s0 |
1,7 |
1,6 |
|
|
4s0 |
1,0 |
1,0 |
|
|
10 |
s0 |
930,0 |
200,0 |
|
2s0 |
1,5 |
1,4 |
|
|
4s0 |
1,0 |
1,0 |
|
|
12 |
s0 |
840,0 |
170,0 |
|
2s0 |
1,3 |
1,2 |
|
|
4s0 |
1,0 |
1,0 |
|
|
15 |
s0 |
860,0 |
170,0 |
|
2s0 |
1,2 |
1,1 |
|
|
4s0 |
1,0 |
1,0 |
|
|
Các giá trị được cho là ARL. Người đọc cần biết rằng độ dài loạt thực tế được lấy để phát hiện thay đổi thực tế sẽ khác nhau và có thể ngắn hơn hoặc dài hơn ARL. Khi điều này được quan tâm đặc biệt, người đọc cần kiểm tra phân bố của độ dài loạt đối với dịch chuyển cụ thể từ đích để biết độ rộng dự kiến của độ dài loạt có thể có. |
|||
Bước 5 – Ước lượng s0 từ dữ liệu giai đoạn thử
a) Đối với mỗi nhóm con, tính độ lệch chuẩn trong nhóm con (s).
b) Tính trung bình độ lệch chuẩn trong nhóm con ![]() .
.
Ước lượng độ lệch chuẩn trong nhóm con, ![]() , trong đó c4 có thể được đọc từ Bảng 18.
, trong đó c4 có thể được đọc từ Bảng 18.
Bảng 18 – Hệ số c4 đối với việc ước lượng độ lệch chuẩn trong nhóm con
|
Cỡ nhóm con, na |
c4 |
|
2 3 4 5 6
7 8 9 10 12 15 20 |
0,797 9 0,886 2 0,921 3 0,940 0 0,951 5
0,959 4 0,965 0 0,969 3 0,972 7 0,977 6 0,982 3 0,986 9 |
|
a Có các giá trị của c4 đối với n > 20. Xem TCVN 9945-2 (ISO 7870-2) hoặc sách hay các tiêu chuẩn khác. |
|
Bước 6 – Xác định giá trị đích, T
a) Giá trị đã cho
Trong kiểm soát chất lượng thống kê hoặc quá trình, phương pháp thích hợp nhất trong việc thiết lập giá trị đích độ lệch chuẩn trong nhóm con như được mô tả trong điểm b) dưới đây. Tuy nhiên, có thể có những trường hợp ưu tiên thiết lập giá trị đích từ một mức s0 giả định. Nếu vậy, độ lệch chuẩn đích trong nhóm con được tính là T = c4s0, trong đó c4 được lấy từ Bảng 18.
b) Giá trị dựa trên hiệu năng
Từ dữ liệu thu được trong giai đoạn thử, thiết lập độ lệch chuẩn đích trong nhóm con bằng với s.
Bước 7 – Thiết lập văn phòng phẩm cusum
Lập bảng cusum (hoặc bổ sung vào bảng cusum hiện có) và xây dựng giấy vẽ đồ thị cusum.
Giấy vẽ đồ thị cusum trong đó cusum với độ lệch chuẩn trong nhóm con được vẽ đồ thị có thể yêu cầu thang đo khác với thang đo được chọn để theo dõi giá trị trung bình. Có thể lấy tỷ lệ thang đo thích hợp bằng cách sử dụng phép tính dưới đây, làm tròn lên hoặc xuống giá trị thích hợp gần nhất.
Khoảng thang đo cusum đối với độ lệch chuẩn trong nhóm con là as0, trong đó a được lấy từ Bảng 19.
Bảng 19 – Hệ số thang đo giấy vẽ đồ thị cusum đối với cusum độ lệch chuẩn trong nhóm con
|
Cỡ nhóm con |
a |
|
2 3 4 5 6 8 10 15 20 |
1,50 1,00 0,85 0,75 0,65 0,55 0,50 0,40 0,35 |
Bước 8 – Lập mặt nạ cusum
Sử dụng các giá trị h và ¦ được chọn trong Bước 3, tính:
a) H = h x ![]() ; và
; và
b) F = ¦ x ![]() .
.
Xây dựng mặt nạ bằng cách sử dụng giá trị H và F tính được và chia tỷ lệ mặt nạ theo thang đo được chọn đối với giấy vẽ đồ thị cusum.
9.5. Tình huống đặc biệt
9.5.1. Độ biến động lớn giữa nhóm con
Trong các trường hợp nhất định, việc cho phép coi một số biến động trung bình giữa nhóm con là một phần của độ biến động ngẫu nhiên trở nên quan trọng. Ví dụ như sự biến thiên nhỏ ở mức trung bình được phát hiện bằng biểu đồ cusum, nhưng không có kế hoạch để loại bỏ chúng. Để ngăn ngừa cusum liên tục hiển thị tình trạng mất kiểm soát, những biến thiên nhỏ này cần được tính đến trong ước lượng độ biến động.
Tính độ lệch chuẩn trung bình giữa nhóm con (được gọi là sai số chuẩn của trung bình), ![]() . Đây có thể là từ dữ liệu giai đoạn thử hoặc một khoảng dữ liệu khác đại diện cho độ biến động. Sử dụng giá
. Đây có thể là từ dữ liệu giai đoạn thử hoặc một khoảng dữ liệu khác đại diện cho độ biến động. Sử dụng giá ![]() trị
trị ![]() trong việc chia tỷ lệ giấy cusum và mặt nạ, thay vì se sử dụng trước đó để thiết lập trung bình.
trong việc chia tỷ lệ giấy cusum và mặt nạ, thay vì se sử dụng trước đó để thiết lập trung bình.
Phụ lục A bao gồm phương pháp hỗ trợ nhận biết sự phù hợp của cách tiếp cận này.
Quy trình này cần đạt hiệu quả mong muốn trong việc giảm số lượng báo hiệu mất kiểm soát nhỏ và “giả” có thể có trên đồ thị cusum và làm cho kiểm soát chất lượng thích hợp hơn.
9.5.2. Dữ liệu “tại một thời điểm”
Một số đối tượng để theo dõi cusum sẽ đưa ra dữ liệu có tính chất xảy ra tại một thời điểm và mọi ý định về phân nhóm dữ liệu như vậy sẽ không có ý nghĩa. Ví dụ, như đã nêu trước đó, là doanh số bán hàng hàng tháng, hoặc nhiệt độ bể chứa hóa chất được sử dụng trong quá trình sản xuất ở đó ghi lại nhiều nhiệt độ lặp lại được thực hiện gần như đồng thời sẽ không cho thấy bất kỳ biến động nào giữa các quan trắc. Trong trường hợp đó, biến động trong nhóm con bằng “không” và không thể vẽ được mặt nạ.
Một ví dụ khác của dữ liệu này là cách xác định điểm số đánh gôn. Một số lỗ có số cú đánh dự kiến khác nhau và người chơi gôn đo lường hiệu năng dựa trên số lần đánh dự kiến cho mỗi lỗ. Tổng các hiệu trở thành cusum.
Cỡ nhóm con là một cũng xảy ra khi việc lấy và/hoặc phân tích mẫu rất tốn kém.
Cách tiếp cận nên là thiết lập cỡ nhóm con bằng một và sau đó làm theo các bước trong 9.3 và tiếp sau đó, lấy cỡ nhóm con là một, nghĩa là n =1. Như vậy, vị trí (mức trung bình) được theo dõi bằng chính các kết quả riêng lẻ trong khi mức biến động được theo dõi bằng độ rộng thể hiện giữa các kết quả liên tiếp.
Đích đối với giá trị trung bình cần là T = ![]() được xác định từ dữ liệu giai đoạn thử, hoặc đích cần là giá trị cho trước. Đích đối với độ rộng là
được xác định từ dữ liệu giai đoạn thử, hoặc đích cần là giá trị cho trước. Đích đối với độ rộng là ![]() được xác định từ sự chênh lệch liên tiếp trong dữ liệu thử, hoặc đặt T = 1,128 s nếu độ lệch chuẩn là giá trị cho trước. Mặc dù cỡ nhóm con là một, cỡ nhóm con hiệu quả khi liên quan đến độ rộng là hai.
được xác định từ sự chênh lệch liên tiếp trong dữ liệu thử, hoặc đặt T = 1,128 s nếu độ lệch chuẩn là giá trị cho trước. Mặc dù cỡ nhóm con là một, cỡ nhóm con hiệu quả khi liên quan đến độ rộng là hai.
9.5.3. Sự phụ thuộc theo thứ tự giữa các quan trắc
Cơ sở cho biểu đồ cusum, như đối với bất kỳ biểu đồ kiểm soát nào, là tính độc lập giữa các điểm được vẽ. Điều này có thể không đúng trong các quá trình hoặc các bộ dữ liệu nhất định, ví dụ: các quá trình trong đó có một số người kiểm soát chu trình khép kín tại nơi làm việc, như bộ điều nhiệt đưa thông tin đến thiết bị gia nhiệt, hoặc quá trình có tính mùa vụ, như dữ liệu doanh thu.
Ảnh hưởng của điều này trên đồ thị cusum có thể nghiêm trọng và tác động đáng kể đến hiệu năng của nó, trong một số trường hợp dẫn đến báo hiệu sai và trong trường hợp khác bỏ qua những thay đổi quan trọng.
Kiểm nghiệm thống kê hiện có sẽ cho thấy dữ liệu là phụ thuộc trình tự và liên kết là “dương” hay “âm”. Phương pháp đơn giản là đo lường sự tương quan giữa dữ liệu ban đầu theo trình tự thiết lập của chúng với dữ liệu tương tự được sau một nấc, nghĩa là kết quả đầu tiên trong dữ liệu ban đầu được so sánh với kết quả thứ hai, kết quả thứ hai được so sánh với kết quả thứ ba, v.v.. Nếu hệ số tương quan tính được lớn hơn “không” thì nó chỉ ra liên kết dương giữa các quan trắc, nghĩa là các kết quả “dịch chuyển” theo cùng một hướng. Nếu hệ số tương quan nhỏ hơn “không” rất nhiều, thể hiện liên kết âm, cho thấy rằng nếu kết quả cao hơn phần trước nó thì kết quả tiếp theo sẽ theo hướng ngược lại, đặc tính chung của quá trình bị điều chỉnh quá mức. Mối tương quan đó được tính dễ dàng bằng cách sử dụng các chương trình bảng tính hoặc gói phần mềm máy tính thống kê khác và phân tích như vậy được khuyến nghị.
Độ rộng hệ số tương quan từ 1 đến +1 và ngưỡng đối với giá trị khác “không” đáng kể sẽ phụ thuộc vào bao nhiêu điểm dữ liệu được sử dụng trong bất kỳ nghiên cứu nào. Nếu bộ dữ liệu nhỏ, trị số dường như lớn đối với hệ số tương quan tuy nhiên có thể không quan trọng về thống kê, trong khi với bộ dữ liệu lớn, hệ số tương quan gần như bằng “không” có thể được hiểu là quan trọng về thống kê. Bảng 20 đưa ra hướng dẫn gần đúng về hệ số tương quan quan trọng.
Bảng 20 – Khoảng tới hạn đối với hệ số tương quan
|
Số điểm dữ liệu “cặp” |
Khoảng tới hạn đối với hệ số tương quana |
|
10 15 20 25 |
±0,45 ±0,37 ±0,33 ±0,30 |
|
a Ở mức ý nghĩa 0,05 (hai phía). |
|
Nếu giá trị hệ số tương quan tính được nằm trong khoảng đã cho trong Bảng 20 thì không có lý do gì để giả định là có sự phụ thuộc về trình tự. Có thể có một số sự phụ thuộc về trình tự kém là cỡ mẫu quá nhỏ để phát hiện.
Nếu phát hiện có sự phụ thuộc về trình tự thì có thể yêu cầu sự hỗ trợ của chuyên gia để xác định hướng tốt nhất. Các hành động có thể bao gồm phân tích quá trình sâu hơn như về nguyên nhân của sự phụ thuộc. Giải pháp cho vấn đề có thể đơn giản hoặc phức tạp. Nếu sự phụ thuộc là do mùa vụ thì có thể khắc phục bằng cách thay đổi đích cho mỗi giai đoạn thời gian. Theo cách này giá trị cusum sẽ độc lập với mùa vụ.
9.5.4 Giá trị bất thường
Cusum đòi hỏi chống các giá trị bất thường. Nếu giá trị bất thường xảy ra, ảnh hưởng của nó đến giá trị cusum có thể lớn và có thể dẫn đến báo hiệu mất kiểm soát sai. Sau đây là phương pháp đơn giản nhưng hiệu quả trong việc bảo vệ cusum chống các giá trị bất thường.
a) Kết quả được coi là giá trị bất thường nếu:
1) trung bình nhóm con lớn hơn ±3se so với giá trị đích; hoặc
2) kết quả riêng lẻ lớn hơn ±3s so với giá trị đích.
Ghi lại kết quả như là giá trị bất thường nhưng không đưa giá trị vào tính cusum trừ khi kết quả tiếp theo nằm ngoài các giới hạn nghi ngờ.
b) Kết quả bị nghi ngờ là giá trị bất thường nếu:
1) trung bình nhóm con lớn hơn ±2se so với giá trị đích; hoặc
2) kết quả riêng lẻ lớn hơn ±2s so với giá trị đích.
Nếu hai kết quả liên tiếp nằm ngoài các giới hạn nghi ngờ thì đưa cả hai kết quả vào phép tính cusum. Điều này luôn luôn dẫn đến báo hiệu mất kiểm soát.
CHÚ THÍCH: Có nhiều phương pháp chặt chẽ hơn (ISO 5727-5) để phát hiện các giá trị bất thường nhưng chúng không hữu dụng trong “thời gian thực”. Phương pháp mô tả ở đây là phương thức thực hiện đơn giản và khả thi.
9.6. Chương trình cusum đối với dữ liệu rời rạc
9.6.1. Số đếm biến cố – Dữ liệu Poisson
9.6.1.1. Khái quát
Dữ liệu đếm được liên quan đến các số đếm biến cố trong đó mỗi cá thể dữ liệu là số đếm của số biến cố cụ thể trong khoảng thời gian hoặc lượng sản phẩm cho trước. Ví dụ: số vụ tai nạn hoặc người vắng mặt mỗi tháng, số hoạt động hoặc số chuyến bay mỗi ngày, số lượng cuộc điện thoại gọi đến mỗi phút, hoặc số lượng không phù hợp trên một đơn vị hoặc lô.
Phân bố Poisson có hai phần cơ bản để vận dụng trong phân tích cusum:
a) như phép xấp xỉ nhị thức phức tạp hơn (xem 9.6.2) khi
n lớn và p nhỏ, lấy n > 20 và p < 0,1;=””>
b) như phân bố theo cách riêng của nó, khi các biến cố xảy ra ngẫu nhiên theo thời gian hay không gian và quan trắc là số các biến cố trong khoảng đã cho.
Tính hợp lệ của mô hình Poisson xoay quanh tính độc lập của các biến cố và sự xuất hiện của chúng tỷ lệ trung bình được giả định là ổn định (trong trường hợp không có nguyên nhân đặc biệt).
Do mô hình Poisson (và nhị thức) thiếu tính đối xứng nên cần sử dụng các quy tắc quyết định khác nhau cho việc đánh giá dịch chuyển theo hướng lên và hướng xuống. Do đó, nếu sử dụng mặt nạ V cắt tỉa, mặt nạ sẽ không đối xứng như trước. Sẽ có các giá trị khác nhau về đường dốc và khoảng quyết định đối với nửa trên và nửa dưới.
Như một sự phức tạp hiển nhiên, nhưng được đưa vào để dễ dàng tính toán, phân bố nhất định đôi khi được tính xấp xỉ bằng phân bố khác. Ví dụ, trong điều kiện nhất định phân bố Poisson hoặc phân bố chuẩn xấp xỉ với nhị thức, và trong điều kiện khác là phân bố chuẩn đối với Poisson.
Trong 9.3 và 9.4, ARL đối với dữ liệu phân bố chuẩn được xác định đơn giản từ các ARL của phân bố chuẩn chuẩn hóa, có trung bình là 0 và độ lệch chuẩn là 1. Phân bố rời rạc không có đặc tính này. Từng tham số cần được tính riêng. Do đó, bảng biểu cho mục đích thiết kế cusum rời rạc được hạn chế với các tổ hợp lựa chọn chỉ dịch chuyển theo hướng đi lên. Gần đây, các chương trình phần mềm sẵn có đã tăng đáng kể lựa chọn các thiết kế cusum đối với dữ liệu rời rạc.
9.6.1.2. Quy tắc chung quyết định cusum đối với dữ liệu rời rạc
Chương trình cusum đối với dữ liệu rời rạc được quy định duy nhất theo loại phân bố dữ liệu và hai tham số, giá trị mốc K và khoảng quyết định H. Các dấu hiệu chính trong lựa chọn các tham số dưới đây:
a) Thiết kế cusum chương trình quyết định chủ yếu là quá trình hai giai đoạn:
1) lựa chọn tổ hợp K và H để đưa ra ARL trong tầm kiểm soát mong muốn; và
2) xác định sự nhanh chóng của đáp ứng báo hiệu tại các dịch chuyển thích hợp khác nhau về trung bình.
b) Cần lựa chọn giá trị mốc K trên cơ sở dịch chuyển quy định về trung bình trong đó đáp ứng được báo hiệu. K thích hợp là tại giá trị giữa trung bình trong tầm kiểm soát và trung bình mất kiểm soát trong đó cusum cần có độ nhạy tối đa. Giá trị K cụ thể phụ thuộc vào loại phân bố dữ liệu và xác định giá trị nào được chấp nhận đối với trung bình.
9.6.1.3. Chương trình cusum đối với dữ liệu số đếm
Bước 1 – Xác định tỷ lệ trung bình thực tế của lần xuất hiện, m, và độ lệch chuẩn, se.
Bước 2 – Lựa chọn tỷ lệ tham chiếu hoặc đích của lần xuất hiện, Tm. Thông thường sẽ lấy giá trị m.
Bước 3 – Quyết định trên quy tắc quyết định thích hợp nhất bằng cách lựa chọn chương trình áp dụng. Lựa chọn ưu tiên là chương trình CS1 với ARL ở mức độ đích ít nhất 1 000, hoặc chương trình CS2 với ARL ở mức độ đích ít nhất 200. Tham khảo Bảng 21.
Bước 4 – Xác định giá trị H và K như sau:
a) đối với Tm (0,1 £ Tm £ 25,0) vào Bảng 21 ở giá trị gần nhất với Tm. Sử dụng phép nội suy tuyến tính giữa các giá trị Tm từ 10,0 đến 25,0; hoặc
b) nếu Tm > 25,0 tham khảo bảng thích hợp trong 9.3 liên quan đến phân bố chuẩn, lúc này sử dụng se= ![]() như xấp xỉ chuẩn đối với Poisson là thích hợp.
như xấp xỉ chuẩn đối với Poisson là thích hợp.
Ví dụ, giả sử Tm = 25. Đối với biến chuẩn có trung bình 25, độ lệch chuẩn 5, H = 24 và K = 28; ARL tương ứng là khoảng 1 500. ARL thực cho biến Poisson với H = 24 và K = 28 là 1 085. ARL rút ngắn này phát sinh từ độ lệch và tính rời rạc của phân bố Poisson.
Bước 5 – Xây dựng và áp dụng mặt nạ V hoặc lập bảng:
a) đối với phân tích biểu đồ: vẽ đồ thị tổng các hiệu (X – Tm) và sử dụng mặt nạ V cắt tỉa với khoảng quyết định, H, và đường dốc, F = (X - Tm); hoặc
b) đối với cusum dạng bảng: tạo tổng các hiệu (X – K), quay lại về không bất cứ khi nào tích lũy là âm. Kiểm nghiệm H đối với báo hiệu sự dịch chuyển.
Bước 6 – Đánh giá hiệu năng ARL của chương trình được lựa chọn ở độ dịch chuyển quan tâm so với giá trị danh nghĩa bằng cách sử dụng Bảng 22.
VÍ DỤ
Bước 2: Tỷ lệ trung bình quy chiếu, Tm = 4.
Bước 3: Sử dụng chương trình CS1.
Bước 4: Tra Bảng 21 tại Tm = 4,0. Ta có, H = 8 và K = 6.
Bước 5 a): Vẽ cusum, xây dựng và áp dụng mặt nạ V (H = 8, F = 2).
Bước 5 b): Lập bảng và xây dựng cusum dạng bảng (H = 8, K = 6).
Bước 6: Hiệu năng chương trình được thể hiện dưới đây. Nếu quá trình đã hoạt động ở mức đích, ARL (L0) là 1 736. Tuy nhiên, ARL sẽ giảm xuống 10 nếu tỷ lệ tăng lên đến 6,60.
|
H |
K |
Tm |
L0 |
|
ARL |
1 000 |
500 |
200 |
100 |
50 |
20 |
10 |
5 |
2 |
|
8,0 |
6,00 |
4,000 |
1 736 |
m |
4,160 |
4,380 |
4,710 |
5,000 |
5,300 |
5,90 |
6,60 |
7,80 |
11,50 |
CHÚ THÍCH: Dữ liệu lấy từ Bảng 22.
9.6.2. Dữ liệu hai lớp – Dữ liệu nhị thức
9.6.2.1. Khái quát
Với dữ liệu được phân lớp, mỗi cá thể dữ liệu được phân loại thuộc về nhiều loại. Thông thường, số loại là hai, cụ thể là tình huống nhị thức trong đó, ví dụ kết quả thường được thể hiện là 0 và 1, hoặc đạt/không đạt, lãi/lỗ, trong/ngoài, hoặc có/không có của đặc trưng cụ thể.
Dữ liệu có hai lớp được gọi là dữ liệu “nhị thức”. Thước đo có thể là nhị thức vốn có, ví dụ có lãi hoặc lỗ, là một ai đó vào hay ra? Đôi khi nó đạt được một cách gián tiếp bằng cách phân loại một số thước đo số khác. Ví dụ, lấy trường hợp khi các cuộc điện thoại được phân loại xem chúng kéo dài hơn 10 phút hay không hoặc có thể là xem chúng có được trả lời trong vòng 6 tiếng chuông hay không.
Bảng 21 – Chương trình CS1 và CS2 đối với dữ liệu số đếm (Poisson) về Tm, H và K
|
Tỷ lệ biến cố đích Tm |
Chương trình CS1 |
Chương trình CS2 |
||
|
H |
K |
H |
K |
|
|
0,100 |
1,5 |
0,75 |
2,0 |
0,25 |
|
0,125 |
2,5 |
0,50 |
2,5 |
0,25 |
|
0,160 |
3,0 |
0,50 |
2,0 |
0,50 |
|
0,200 |
3,5 |
0,50 |
2,5 |
0,50 |
|
0,250 |
4,0 |
0,50 |
3,0 |
0,50 |
|
0,320 |
3,0 |
1,00 |
4,0 |
0,50 |
|
0,400 |
2,5 |
1,50 |
3,0 |
1,00 |
|
0,500 |
3,0 |
1,50 |
2,0 |
1,50 |
|
0,640 |
3,5a hoặc 4,0 |
1,50 |
2,0 |
2,00 |
|
0,800 |
5,0 |
1,50 |
3,5 |
1,50 |
|
1,000 |
5,0 |
2,00 |
5,0 |
1,50 |
|
1,250 |
4,0 |
3,00 |
5,0 |
2,00 |
|
1,600 |
5,0 |
3,00 |
4,0 |
3,00 |
|
2,000 |
7,0a hoặc 8,0 |
3,00 |
5,0 |
3,00 |
|
2,500 |
7,0 |
4,00 |
5,0 |
4,00 |
|
3,200 |
7,0 |
5,00 |
5,0 |
5,00 |
|
4,000 |
8,0 |
6,00 |
6,0 |
6,00 |
|
5,000 |
9,0 |
7,00 |
7,0 |
7,00 |
|
6,400 |
9,0 |
9,00 |
9,0 |
8,00 |
|
8,000 |
9,0 |
11,00 |
9,0 |
10,00 |
|
10,000 |
11,0 |
13,00 |
11,0 |
12,00 |
|
15,000 |
16,0 |
18,00 |
11,0 |
18,00 |
|
20,000 |
20,0 |
23,00 |
14,0 |
23,00 |
|
25,000 |
24,0 |
28,00 |
17,0 |
28,00 |
|
CHÚ THÍCH 1: Chương trình CS1 đưa ra các ARL đích từ 1 000 đến 2 000 quan trắc. Chương trình CS2 đưa ra các ARL đích từ 200 đến 400 quan trắc. CHÚ THÍCH 2: Đối với Tm < 1,=”” việc=”” chia=”” thang=”” đo=”” được=”” khuyến=”” nghị=”” là=”” các=”” quan=”” trắc=”” riêng=”” có=”” thông=”” tin=”” hạn=”” chế.=”” xác=”” định=”” số=”” quan=”” trắc=”” trung=”” bình=”” cần=”” thiết=”” để=”” tạo=”” ra=”” một=”” biến=”” cố,=”” đó=”” là=””>Tm. Làm tròn giá trị này lên số nguyên thích hợp trong việc vẽ đồ thị và chấp nhận nó như là khoảng nằm ngang đối với biểu đồ cusum. Đánh dấu thang đo cusum thẳng đứng theo các khoảng có cùng độ dài như thang đo nằm ngang và ký hiệu chúng, theo số nguyên chẵn liên tiếp trên hoặc dưới “không”, nghĩa là 0, +2, +4, v.v.., -2, -4, v.v… CHÚ THÍCH 3: Lựa chọn giá trị Tm lên đến 10 dựa trên dãy số ưu tiên R 10 bằng cách đưa ra mười tỷ lệ xấp xỉ bằng nhau giữa các mục kế tiếp trong mỗi nhóm mười. CHÚ THÍCH 4: Đối với Tm từ 10 đến 25, đưa ra giá trị có khoảng cách bằng nhau để tạo thuận lợi cho nội suy. Có thể thu được chương trình trung gian trong vùng này bằng nội suy tuyến tính trong cả H và K và làm tròn thành số nguyên. Ưu tiên làm tròn cả H và K theo cùng một cách. |
||||
|
a Giá trị thấp hơn của H cho L0 thấp hơn 1 000 một chút; giá trị cao hơn cho L0 bằng 2 000. |
||||
Bảng 22 – Các đặc trưng ARL cho chương trình cusum liên quan tới H và K đối với dữ liệu số đếm (Poisson)
|
Tham số |
Chương trình CS1 |
Chương trình CS2 |
Tỷ lệ xuất hiện trung bình tại các giá trị ARL đã biết |
|||||||||||
|
H |
K |
Tm |
L0 |
Tm |
L0 |
1 000 |
500 |
200 |
100 |
50 |
20 |
10 |
5 |
2 |
|
2,0 |
0,25 |
— |
— |
0,100 |
212 |
0,057 |
0,072 |
0,102 |
0,135 |
0,179 |
0,23 |
0,43 |
0,74 |
1,99 |
|
2,5 |
0,25 |
— |
— |
0,125 |
227 |
0,078 |
0,097 |
0,131 |
0,166 |
0,220 |
0,33 |
0,49 |
0,82 |
2,12 |
|
2,0 |
0,50 |
— |
|
0,160 |
230 |
0,095 |
0,121 |
0,168 |
0,220 |
0,280 |
0,42 |
0,59 |
0,91 |
2,09 |
|
1,5 |
0,75 |
0,100 |
1 033 |
— |
— |
0,120 |
0,130 |
0,181 |
0,240 |
0,320 |
0,46 |
0,66 |
0,99 |
2,11 |
|
2,5 |
0,50 |
0,125 |
1 371 |
0,200 |
278 |
0,138 |
0,167 |
0,220 |
0,280 |
0,350 |
0,49 |
0,68 |
1,05 |
2,32 |
|
3,0 |
0,50 |
0,160 |
1 609 |
0,250 |
264 |
0,179 |
0,210 |
0,270 |
0,330 |
0,400 |
0,56 |
0,77 |
1,12 |
2,74 |
|
3,5 |
0,50 |
0,200 |
1 461 |
— |
— |
0,220 |
0,250 |
0,310 |
0,370 |
0,440 |
0,60 |
0,84 |
1,31 |
3,02 |
|
4,0 |
0,50 |
0,250 |
966 |
0,320 |
271 |
0,250 |
0,280 |
0,340 |
0,400 |
0,470 |
0,65 |
0,91 |
1,41 |
3,37 |
|
3,0 |
1,00 |
0,320 |
1 174 |
0,400 |
446 |
0,330 |
0,390 |
0,480 |
0,570 |
0,690 |
0,91 |
1,17 |
1,63 |
3,08 |
|
2,0 |
1,50 |
— |
— |
0,500 |
260 |
0,360 |
0,420 |
0,540 |
0,640 |
0,780 |
1,04 |
1,32 |
1,78 |
3,17 |
|
2,5 |
1,50 |
0,400 |
1 103 |
— |
— |
0,410 |
0,490 |
0,610 |
0,730 |
0,890 |
1,15 |
1,46 |
1,93 |
3,37 |
|
2,0 |
2,00 |
— |
— |
0,640 |
221 |
0,420 |
0,510 |
0,650 |
0,790 |
0,970 |
1,27 |
1,58 |
2,09 |
3,44 |
|
3,0 |
1,50 |
0,500 |
1 475 |
— |
— |
0,540 |
0,620 |
0,740 |
0,660 |
1,010 |
1,28 |
1,60 |
2,12 |
3,85 |
|
3,5 |
1,50 |
0,640 |
833 |
0,800 |
249 |
0,620 |
0,700 |
0,830 |
0,950 |
1,100 |
1,38 |
1,70 |
2,26 |
3,74 |
|
4,0 |
1,50 |
0,640 |
1 843 |
— |
— |
0,700 |
0,790 |
0,920 |
1,040 |
1,190 |
1,47 |
1,81 |
2,38 |
4,44 |
|
5,0 |
1,50 |
0,800 |
1 439 |
1,000 |
274 |
0,840 |
0,920 |
1,040 |
1,160 |
1,310 |
1,60 |
1,95 |
2,64 |
5,25 |
|
5,0 |
2,00 |
1,000 |
1 904 |
1,250 |
259 |
1,090 |
1,190 |
1,350 |
1,500 |
1,680 |
2,00 |
2,37 |
3,09 |
5,90 |
|
4,0 |
3,00 |
1,250 |
1 867 |
1,600 |
354 |
1,380 |
1,530 |
1,750 |
1,950 |
2,200 |
2,61 |
3,04 |
3,76 |
6,35 |
|
5,0 |
3,00 |
1,600 |
1 118 |
2,000 |
188 |
1,640 |
1,770 |
1,940 |
2,180 |
2,420 |
2,83 |
3,29 |
4,07 |
6,60 |
|
7,0 |
3,00 |
2,000 |
894 |
— |
— |
1,980 |
2,110 |
2310 |
2,490 |
2,710 |
3,09 |
3,57 |
4,59 |
7,55 |
|
8,0 |
3,00 |
2,000 |
1 927 |
— |
— |
2,110 |
2,330 |
2430 |
2,600 |
2,810 |
3,23 |
3,78 |
4,80 |
8,40 |
|
5,0 |
4,00 |
— |
— |
2,500 |
300 |
2,170 |
2,350 |
2600 |
2,870 |
3,160 |
3,63 |
4,16 |
5,00 |
7,60 |
|
7,0 |
4,00 |
2,500 |
1 761 |
— |
— |
2,620 |
2,800 |
3,050 |
3,260 |
3,450 |
3,99 |
4,53 |
5,60 |
8,85 |
|
5,0 |
5,00 |
— |
— |
3,200 |
245 |
2,730 |
2,940 |
3,270 |
3,560 |
3,890 |
4,45 |
5,00 |
6,00 |
8,50 |
|
7,0 |
5,00 |
3,200 |
1 318 |
— |
— |
3,280 |
3,480 |
3,780 |
4,030 |
4,320 |
4,88 |
5,50 |
6,50 |
9,80 |
|
6,0 |
6,00 |
|
— |
4,000 |
373 |
3,640 |
3,880 |
4,240 |
5,550 |
4,930 |
5,50 |
6,20 |
7,20 |
10,40 |
|
8,0 |
6,00 |
4,000 |
1 736 |
— |
— |
4,160 |
4,380 |
4,710 |
5,000 |
5,300 |
5,90 |
6,60 |
7,80 |
11,50 |
|
7,0 |
7,00 |
— |
— |
5,000 |
348 |
4,600 |
4,840 |
5,200 |
5,600 |
5,900 |
6,60 |
7,30 |
8,50 |
11,60 |
|
9,0 |
7,00 |
5,000 |
1 268 |
— |
— |
5,100 |
5,300 |
5,700 |
6,000 |
6,400 |
6,90 |
7,70 |
9,10 |
13,50 |
|
9,0 |
8,00 |
— |
— |
6,400 |
226 |
5,800 |
6,100 |
6,500 |
6,800 |
7,200 |
7,90 |
8,60 |
10,00 |
14,20 |
|
9,0 |
9,00 |
6,400 |
1 351 |
— |
— |
6,500 |
6,000 |
7,200 |
7,600 |
8,100 |
8,80 |
9,60 |
11,10 |
15,20 |
|
9,0 |
10,00 |
— |
— |
8,000 |
213 |
7,200 |
7,600 |
8,000 |
8,400 |
8,900 |
9,70 |
10,50 |
11,90 |
16,20 |
|
9,0 |
11,00 |
8,000 |
946 |
— |
— |
8,000 |
8,300 |
8,600 |
9,300 |
9,800 |
10,50 |
11,40 |
13,00 |
16,40 |
|
11,0 |
12,00 |
— |
— |
10,000 |
234 |
9,300 |
9,600 |
10,100 |
10,500 |
11,000 |
11,90 |
12,80 |
14,60 |
19,80 |
|
11,0 |
13,00 |
10,000 |
1 052 |
— |
— |
10,000 |
10,400 |
11,000 |
11,400 |
11,900 |
12,70 |
13,70 |
15,50 |
20,30 |
|
11,0 |
18,00 |
— |
— |
15,000 |
214 |
13,900 |
14,300 |
15,100 |
15,600 |
16,300 |
17,40 |
18,50 |
20,40 |
25,90 |
|
16,0 |
18,00 |
15,000 |
1 289 |
— |
— |
15,100 |
15,500 |
16,100 |
16,500 |
17,200 |
18,20 |
19,40 |
21,70 |
29,10 |
|
14,0 |
23,00 |
— |
— |
20,000 |
215 |
18,800 |
19,300 |
20,100 |
20,700 |
21,400 |
22,60 |
24,00 |
26,20 |
32,90 |
|
20,0 |
23,00 |
20,000 |
1 140 |
— |
— |
20,100 |
20,500 |
21,100 |
21,700 |
22,300 |
23,50 |
24,90 |
27,60 |
36,80 |
|
17,0 |
28,00 |
— |
— |
25,000 |
222 |
23,700 |
24,300 |
25,100 |
25,800 |
26,500 |
27,80 |
29,30 |
31,90 |
40,00 |
|
24,0 |
28,00 |
25,000 |
1 085 |
— |
— |
25,100 |
25,500 |
26,200 |
26,700 |
27,400 |
28,70 |
30,40 |
33,50 |
44,90 |
|
CHÚ THÍCH: Bảng này liên quan đến sự dịch chuyển đi lên của trung bình. |
||||||||||||||
Các điều kiện cần được thỏa mãn đối với phân bố nhị thức được nêu dưới đây:
a) Có số phép thử cố định, n.
b) Mỗi lần thử chỉ có thể có hai kết quả. c) Phép thử là độc lập.
d) Có xác suất “thành công”, p, không đổi trong mỗi lần thử.
e) Biến là tổng số lần “thành công” trong n phép thử.
Phân bố nhị thức tính toán rất phức tạp, vì vậy, khi xử lý các ARL và chuẩn mực quyết định, có thể sử dụng phân bố khác như là phép xấp xỉ với nhị thức.
Vì hàng loạt các giá trị có thể có của hai tham số phân bố nhị thức, n (thường tương ứng với cỡ mẫu) và p (tỷ lệ cá thể có thuộc tính quan tâm), nên không thể đưa ra bảng hoàn chỉnh cho tất cả các sự kết hợp. Tuy nhiên, các quy trình gần đúng có thể áp dụng trong nhiều tình huống. Những quy trình này được đưa ra dưới đây.
– Tình huống 1: Nếu Tm < 0,1=”” (nghĩa=”” là=”” tỷ=”” lệ=”” đích,=”” hoặc=”” tham=”” chiếu,=”” dưới=”” 10=”” %),=”” sử=”” dụng=”” chương=”” trình=”” thích=”” hợp=”” đối=”” với=”” biến=”” poisson=”” với=””>Tm = np.
Tình huống 2: Nếu Tm > 20 (nghĩa là số trung bình “các biến cố” cho mỗi mẫu trong các điều kiện đích vượt quá 20), sử dụng chương trình thích hợp cho phân bố chuẩn.
9.6.2.2 Tình huống 1: Tp <> – Chương trình dựa trên Poisson
Mặc dù ở đây phân bố nhị thức là thích hợp, nhưng sử dụng rất phức tạp và có thể lấy xấp xỉ bằng phân bố Poisson. Sử dụng phương pháp từng bước được mô tả trong 9.6.1.3 nhưng với Tm = np. Poisson sẽ luôn đưa ra ARL tại đích, ngắn hơn đối với trường hợp nhị thức, nhưng các ARL ở các dịch chuyển đáng kể từ các điều kiện đích kết hợp chặt chẽ với cùng tỷ lệ trung bình xuất hiện biến cố.
VÍ DỤ
Bước 2: Lấy n = 20 và p = 0,025, vì vậy np = 0,5, và giá trị quy chiếu, Tm = 0,5.
Bước 3: Sử dụng chương trình CS1.
Bước 4: Tra Bảng 21 ở Tm = 0,5. Ta có, H = 3 và K =1,5.
Bước 5 a): Vẽ đồ thị cusum, xây dựng và áp dụng mặt nạ V (H = 3, F = 1,0).
Bước 5 b): Lập bảng và xây dựng cusum dạng bảng (H = 3, K = 1,5).
Bước 6: Hiệu năng của chương trình được thể hiện dưới đây. Nếu quá trình hoạt động ở mức đích, ARL (L0) là 1 475. Tuy nhiên, ARL sẽ giảm xuống 10 nếu tỷ lệ tăng lên đến 1,60, nghĩa là p = 0,080.
|
H |
K |
Tm |
L0 |
|
ARL |
1 000 |
500 |
200 |
100 |
50 |
20 |
10 |
5 |
2 |
|
3,0 |
1,50 |
0,500 |
1 475 |
m |
0,540 |
0,620 |
0,740 |
0,860 |
1,010 |
1,28 |
1,60 |
2,12 |
3,85 |
CHÚ THÍCH: Dữ liệu được lấy từ Bảng 22.
9.6.2.3 Tình huống 2: Tm > 20 – Chương trình dựa trên chuẩn
Trong tình huống 2, chọn cặp tham số h, ¦ phù hợp, ví dụ: 5, 0,5, đối với biến chuẩn tương ứng. Khi đó, tham số cusum đối với nhị thức thu được là:
![]() , làm tròn H đến số nguyên gần nhất.
, làm tròn H đến số nguyên gần nhất.
![]() , làm tròn K đến số nguyên gần nhất.
, làm tròn K đến số nguyên gần nhất.
![]() , làm tròn F đến số nguyên gần nhất.
, làm tròn F đến số nguyên gần nhất.
VÍ DỤ
Bước 2: Lấy n = 80 và Tp = 0,3, h = 5 và f = 0,5.
Bước 4: ![]()
![]()
![]()
Bước 5 a): Vẽ đồ thị cusum, xây dựng và áp dụng mặt nạ V (H = 20, F = 2).
Bước 5 b): Lập bảng, xây dựng cusum dạng bảng (H = 20, K = 26).
Bước 6: Nếu quá trình hoạt động ở mức đích ARL (L0) là xấp xỉ 930. Tuy nhiên, ARL sẽ giảm xuống gần 10 nếu tỷ lệ (p) tăng lên 0,35.
PHỤ LỤC A
(tham khảo)
Phương pháp Von Neumann
Khi lập biểu đồ cusum cho mục đích trình bày dữ liệu, việc lựa chọn quy trình để đo độ biến động có thể chủ yếu là trên cơ sở tính chất của dữ liệu, phương pháp lấy mẫu và thuận lợi cho tính toán. Tuy nhiên, khi thực hiện kiểm nghiệm thống kê đối với các điểm thay đổi hoặc sự dịch chuyển về mức, cần thận trọng trong việc lựa chọn và cần xem xét khả năng phụ thuộc về trình tự giữa các giá trị liên tiếp, hoặc các hiện tượng theo chu kỳ.
Phép kiểm nghiệm về sự bất thường chung hữu ích trong dãy các quan trắc từ đó sai số chuẩn được ước lượng dưới đây.
1. Tính ![]()
2. Tính ![]()
3. Đếm số nhóm con, k.
4. Tính 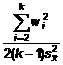
5. Tính ![]()
Nếu giá trị tính được trong Bước 4 cao hơn biên trên ở Bước 5, có nghĩa là sự tương quan dãy âm, ví dụ: kiểm soát quá mức hoặc thay đổi. Giá trị thấp hơn biên dưới có thể xảy ra do chu kỳ hoặc các dạng thức khác của tương quan chuỗi dương, ví dụ: tác động trễ, hoặc thay đổi mức trung bình theo trình tự các quan trắc, thay đổi nấc, độ trôi, xu hướng thường xuyên hay không thường xuyên.
Ngoài ra, có thể đánh giá giá trị tính được trong bước 4 từ Bảng A.1 là 0,05 điểm xác suất (hai đuôi).
Bảng A.1 – Điểm xác suất (hai đuôi) đối với kiểm nghiệm von Neumann
|
Số nhóm con |
Giá trị tới hạn dưới |
Giá trị tới hạn trên |
|
20 |
0,58 |
1,42 |
|
30 |
0,65 |
1,35 |
|
50 |
0,73 |
1,27 |
|
75 |
0,78 |
1,22 |
|
150 |
0,84 |
1,16 |
|
200 |
0,86 |
1,14 |
PHỤ LỤC B
(tham khảo)
Ví dụ về cusum dạng bảng
Giá trị trung bình trong quá khứ là 35 và giá trị độ lệch chuẩn là 6 đã được thiết lập và sử dụng như các tham số cho biểu đồ Shewhart và biểu đồ cusum. Giá trị đích đã được thiết lập là 35.
Hai mươi bốn ngày dữ liệu đã được thu thập: 25,8; 33,4; 31,6; 26,0; 36,4; 33,0; 35,8; 41,8; 44,2; 37,2; 35,0; 41,8; 33,4; 38,4; 30,2; 33,8; 42,6; 39,6; 32,0; 48,4; 44,6; 43,0; 40,8 và 50,6.
Biểu đồ Shewhart của dữ liệu được thể hiện trong Hình B.1. Không có báo hiệu nào được xác định khi sử dụng kiểm nghiệm biểu đồ Shewhart chuẩn.

Hình B.1 – Biểu đồ Shewhart của giá trị trung bình mỗi ngày
Đồ thị cusum của dữ liệu được thể hiện trong Hình B.2. Biểu đồ thể hiện “báo hiệu” vào ngày 24. Biểu đồ Shewhart trong Hình B.1 không phát hiện sự thay đổi này.
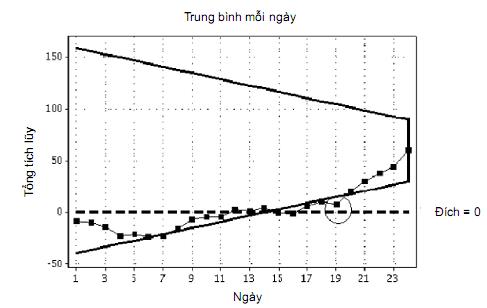
Hình B.2 – Đồ thị cusum và mặt nạ V trung bình mỗi ngày
Dạng bảng của cusum này được thể hiện trong Bảng B.1 dưới đây.
Bảng B.1 – Cusum dạng bảng của dữ liệu trung bình mỗi ngày
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
|
Ngày |
Trung bình mỗi ngày (X) |
(X – T – F) |
Tổng “cao” |
Số “cao” |
(X – T – F) |
Tổng “thấp” |
Số “thấp” |
|
0 |
|
|
15,0 |
0 |
|
-15,0 |
0 |
|
1 |
25,8 |
-12,2 |
2,8 |
1 |
-6,2 |
-21,2 |
1 |
|
2 |
33,4 |
-4,6 |
0,0 |
0 |
1,4 |
-19,8 |
2 |
|
3 |
31,6 |
-6,4 |
0,0 |
0 |
-0,4 |
-20,2 |
3 |
|
4 |
26,0 |
-12,0 |
0,0 |
0 |
-6,0 |
-26,2 |
4 |
|
5 |
36,4 |
-1,6 |
0,0 |
0 |
4,4 |
-21,8 |
5 |
|
6 |
33,0 |
-5,0 |
0,0 |
0 |
1,0 |
-20,8 |
6 |
|
7 |
35,8 |
-2,2 |
0,0 |
0 |
3,8 |
-17,0 |
7 |
|
8 |
41,8 |
3,8 |
3,8 |
1 |
9,8 |
-7,2 |
8 |
|
9 |
44,2 |
6,2 |
10,0 |
2 |
12,2 |
0,0 |
0 |
|
10 |
37,2 |
-0,8 |
9,2 |
3 |
5,2 |
0,0 |
0 |
|
11 |
35,0 |
-3,0 |
6,2 |
4 |
3,0 |
0,0 |
0 |
|
12 |
41,8 |
3,8 |
10,0 |
5 |
9,8 |
0,0 |
0 |
|
13 |
33,4 |
-4,6 |
5,4 |
6 |
1,4 |
0,0 |
0 |
|
14 |
38,4 |
0,4 |
5,8 |
7 |
6,4 |
0,0 |
0 |
|
15 |
30,2 |
-7,8 |
0,0 |
0 |
-1,8 |
-1,8 |
1 |
|
16 |
33,8 |
-4,2 |
0,0 |
0 |
1,8 |
0,0 |
0 |
|
17 |
42,6 |
4,6 |
4,6 |
1 |
10,6 |
0,0 |
0 |
|
18 |
39,6 |
1,6 |
6,2 |
2 |
7,6 |
0,0 |
0 |
|
19 |
32,0 |
-6,0 |
0,2 |
3 |
0,0 |
0,0 |
0 |
|
20 |
48,4 |
10,4 |
10,6 |
4 |
16,4 |
0,0 |
0 |
|
21 |
44,6 |
6,6 |
17,2 |
5 |
12,6 |
0,0 |
0 |
|
22 |
43,0 |
5,0 |
22,2 |
6 |
11,0 |
0,0 |
0 |
|
23 |
40,8 |
2,8 |
25,0 |
7 |
8,8 |
0,0 |
0 |
|
24 |
50,6 |
12,6 |
37,6 |
8 |
18,6 |
0,0 |
0 |
|
CHÚ THÍCH: T = 35; f = 0,5s; h = 5 s. |
|||||||
Cusum này sử dụng “đáp ứng ban đầu nhanh” (FIR), vì vậy giá trị bắt đầu được đặt ở “Ngày 0” trong cột “tổng cao” và “tổng thấp”. Giá trị này tương ứng bằng +2,5s và -2,5s, hoặc +15,0 và -15,0. Tương tự, 0 đã được đặt trong cột “số cao” và “số thấp” ở Ngày 0. Vì h = 5s, giới hạn đối với báo hiệu cusum tương ứng là +30 và -30.
Giá trị đối với “Ngày 1” là 25,8. Tính toán cho cột (3) như sau:
25,8 – 35 – 3 = -12,2
Giá trị 12,2 được cộng vào giá trị “tổng cao” trước đó là 15,0, kết quả là 2,8. Vì “2,8” là dương, cộng “1” vào cột “số cao” đối với giá trị trước đó, nghĩa là 0. Số đếm “số cao” mới là 1. Tính toán cho cột (6) là:
25,8 – 35 + 3 = -6,2
Giá trị 6,2 được cộng vào giá trị “tổng thấp” trước đó là -15,0, kết quả là -21,2. Vì “-21,2” là âm, “1” được cộng vào cột “số thấp” đối với giá trị trước đó, nghĩa là 0. “Số thấp” mới là 1.
Việc tính toán này dường như nhàm chán, nhưng hình dung là sử dụng máy tính để thực hiện các tính toán này.
Giá trị đối với “Ngày 2” là 33,4. Tính toán cho cột (3) như sau:
33,4 – 35 – 3 = -4,6
Giá trị -4,6 được cộng vào giá trị “tổng cao” trước đó là 2,8, kết quả là -1,8. Vì giá trị này âm, giá trị “tổng cao” được thay đổi về 0 và số đếm “số cao” cũng được thay đổi về 0, nghĩa là đối với phía này của cusum, chỉ giá trị cusum “dương” mới được “đếm”.
Tính toán cho cột (6) là:
33,4 – 35 + 3 = 1,4
Giá trị 1,4 được cộng vào giá trị “tổng thấp” trước đó là 21,2, kết quả là -19,8. Như trên, vì “-19,8” âm, nên cộng “1” vào cột “số thấp” đối với giá trị trước của nó, nghĩa là “số thấp” mới bằng 2.
Quy trình này tiếp tục cho đến khi “tổng cao” hoặc “tổng thấp” vượt quá giá trị h (30 hoặc -30, trong ví dụ này). Điều này xảy ra vào “Ngày 24” khi giá trị “tổng cao” là 37,6.
Ước lượng khi “dịch chuyển” xảy ra và lượng “dịch chuyển” có thể thu được từ bảng. Chú thích từ Bảng B.1 ảnh hưởng đến giá trị FIR trong cả “tổng cao” và “tổng thấp” giảm tương đối nhanh nếu quá trình gần đích. Nếu không, thường sẽ thu được báo hiệu “tổng cao” hoặc “tổng thấp”.
Trong ví dụ này, khi thu được báo hiệu “tổng cao”, “số cao” là 8. Điều này gợi ý có sự thay đổi xảy ra giữa “Ngày 16” và “Ngày 17”. Dịch chuyển ước lượng, giả định rằng FIR đã “triệt tiêu”, là:
|
F + |
Tổng cao |
|
Số cao |
Nếu “dịch chuyển” được chỉ ra là âm thì ước lượng được tính bằng:
|
– F – |
Tổng thấp |
|
Số thấp |
Vì “tổng cao” vượt quá giá trị h là 30, dịch chuyển ước lượng là:
|
F + |
Tổng cao |
= |
|
Số cao |
CHÚ THÍCH: Tám giá trị cuối cùng của dữ liệu ban đầu đã được chuyển lên trên bằng xấp xỉ một độ lệch chuẩn, nghĩa là 6 đơn vị. Cusum đã xác định vị trí chính xác của dịch chuyển và dịch chuyển ước lượng là 7,7 không sai khác đáng kể so với 6.
Hình B.3 thể hiện đồ thị cusum dạng bảng.
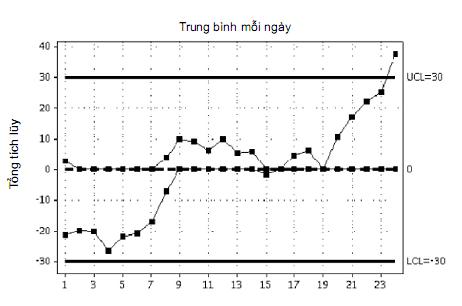
Hình B.3 – Đồ thị cusum dạng bảng đối với trung bình mỗi ngày
PHỤ LỤC C
(tham khảo)
Ước lượng điểm thay đổi khi xảy ra thay đổi theo nấc
Có thể đánh giá xem quá trình trong trạng thái kiểm soát hay không từ các biểu đồ kiểm soát bằng cách sử dụng chuẩn mực cụ thể, nhưng các biểu đồ kiểm soát không thể xác định nguyên nhân ấn định. Tuy nhiên biểu hiện của các đồ thị trước trên biểu đồ kiểm soát có thể đưa ra thông tin để tìm kiếm nguyên nhân ấn định. Đây là vai trò quan trọng của ước lượng về điểm thay đổi.
Trong trường hợp trung bình quá trình m(t) thay đổi theo nấc, điểm thay đổi là t như thể hiện trong công thức:
![]()
Biểu đồ cusum có hiệu năng tốt đối với hàm ước lượng điểm thay đổi. Hàm ước lượng điểm thay đổi là thời điểm khi đường đi của cusum chệch ra bên ngoài cạnh của mặt nạ V như được thể hiện trong Hình C.1.
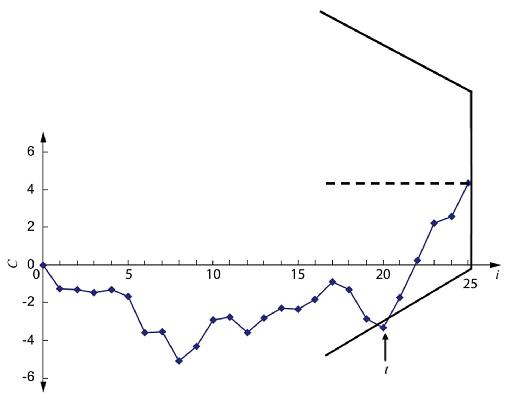
Hình C.1 – Ước lượng điểm thay đổi bằng cách sử dụng mặt nạ V cắt tỉa
Hình C.2 thể hiện phân bố hàm ước lượng từ biểu đồ cusum, trong trường hợp chương trình CS1 (h = 0,5, ¦ = 0,5). Cần xem xét sai lầm loại 1 vì điểm thay đổi chỉ được ước lượng sau khi biểu đồ chỉ ra báo hiệu. Do đó, phân bố trong Hình C.2 được suy ra với điều kiện là sai lầm loại 1 không xảy ra.
Phân bố là một mốt và mô hình của nó giống với điểm thay đổi thực, t = 10. Mặc dù độ dịch chuyển không quá lớn trong trường hợp Hình C.2, đó là d = 1,0se = D, nhưng cách tiếp cận này là thích hợp.
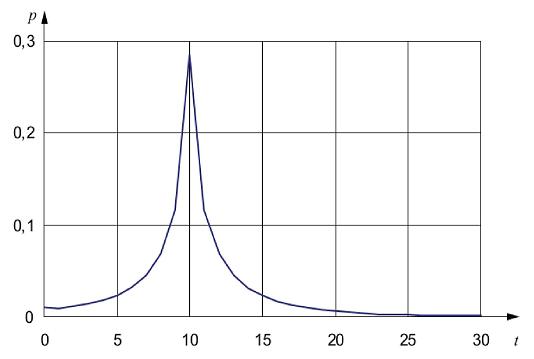
CHÚ THÍCH: Đối với mặt nạ V cắt tỉa có các tham số h = 5,0, ¦ = 0,5, D = 10 và t = 10.
Hình C.2 – Phân bố ước lượng của điểm thay đổi bằng cách sử dụng cusum
THƯ MỤC TÀI LIỆU THAM KHẢO
[1] NISHINA, K. Estimation of the change-point from cumulative sum tests. Reports of Statistical Application Research, JUSE, 33(4), 1986 (Ước lượng điểm thay đổi từ kiểm nghiệm tổng tích lũy. Báo cáo nghiên cứu ứng dụng thống kê)
[2] NISHINA, K. Estimation of the amount of shift using cumulative sum tests. Reports of Statistical Application Research, JUSE, 35(3), 1988 (Ước lượng lượng độ dịch chuyển bằng cách sử dụng kiểm nghiệm tổng tích lũy. Báo cáo nguyên cứu ứng dụng thống kê)
[3] NISHINA, K. A comparison of control charts from the viewpoint of change-point estimation. Quality and Reliability Engineering International, 8, 1992 (So sánh biểu đồ kiểm soát từ quan điểm về ước lượng điểm thay đổi. Chất lượng và độ tin cậy về kỹ thuật quốc tế)
[4] TCVN 6910-5 (ISO 5725-5), Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo – Phần 5: Các phương pháp khác xác định độ chụm của phương pháp đo tiêu chuẩn
[5] TCVN 9945-1 (ISO 7870-1), Biểu đồ kiểm soát – Phần 1: Hướng dẫn chung
[6] TCVN 9945-2 (ISO 7870-2), Biểu đồ kiểm soát – Phần 2: Biểu đồ kiểm soát Shewhart
[7] TCVN ISO 9000 (ISO 9000), Hệ thống quản lý chất lượng – Cơ sở và từ vựng
[8] BS 5703, Guide to data analysis, quality control and improvement using cusum techniques (Hướng dẫn phân tích dữ liệu, kiểm soát và cải tiến chất lượng bằng cách sử dụng kỹ thuật cusum).
MỤC LỤC
Lời nói đầu
Lời giới thiệu
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Thuật ngữ và định nghĩa, chữ viết tắt và ký hiệu
3.1. Thuật ngữ và định nghĩa
3.2. Chữ viết tắt
3.3. Ký hiệu
4. Đặc điểm chính của biểu đồ tổng tích lũy (cusum)
5. Các bước cơ bản trong xây dựng biểu đồ cusum – Trình bày bằng đồ thị
6. Ví dụ về đồ thị cusum – Điện áp động cơ
6.1. Quá trình
6.2. Đồ thị kết quả đơn giản
6.3. Biểu đồ kiểm soát chuẩn đối với các kết quả riêng lẻ
6.4. Biểu đồ cusum – Tổng quan
6.5. Xây dựng biểu đồ cusum
6.6. Giải thích biểu đồ cusum
6.7. Sơ đồ Manhattan
7. Quy tắc cơ bản của việc ra quyết định dựa trên cusum
7.1. Nhu cầu đối với các quy tắc quyết định
7.2. Cơ sở ra quyết định
7.3. Đo lường hiệu quả của quy tắc quyết định
8. Loại chương trình quyết định cusum
8.1. Loại mặt nạ V
8.2 .Mặt nạ V cắt tỉa
8.3. Cách tiếp cận thiết kế thay thế
8.4. Mặt nạ V nửa parabôn
8.5. Mặt nạ V mũi hếch
8.6. Mặt nạ V hoàn chỉnh
8.7. Cusum đáp ứng ban đầu nhanh (FIR)
8.8. Cusum bảng
9. Phương pháp cusum đối với kiểm soát quá trình và chất lượng
9.1. Tính chất thay đổi cần phát hiện
9.2. Lựa chọn giá trị đích
9.3. Chương trình cusum đối với việc theo dõi vị trí
9.4. Chương trình cusum đối với độ biến động theo dõi
9.5. Tình huống đặc biệt
9.6. Chương trình cusum đối với dữ liệu rời rạc
Phụ lục A (tham khảo) Phương pháp Von Neumann
Phụ lục B (tham khảo) Ví dụ về cusum dạng bảng
Phụ lục C (tham khảo) Ước lượng điểm thay đổi khi xảy ra thay đổi theo nấc
Thư mục tài liệu tham khảo


